冀教版七年级数学上册 1.8 有理数的乘法课件(21张PPT)
文档属性
| 名称 | 冀教版七年级数学上册 1.8 有理数的乘法课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 16:45:50 | ||
图片预览








文档简介
(共21张PPT)
学习目标
1.理解有理数乘法法则,能利用有理数乘法法则计算两个数的乘法。
2.理解有理数倒数的意义,会求一个有理数的倒数。
3.能说出有理数乘法法则,能正确运用有理数乘法法则。
教学重、难点
重点:有理数乘法法则的应用,倒数的定义,并会求。
难点:有理数乘法法则的推导过程。
L
O
如图,有一只蜗牛沿直线L爬行,它现在的位置恰好在L
上的一点O。
1、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
2、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
4、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
3、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
提出问题,导入新课
2、如果3分钟以后记为+3分钟,那么3分钟以前应该记为
。
1、如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为
。
-2cm
-3分钟
O
2
4
6
8
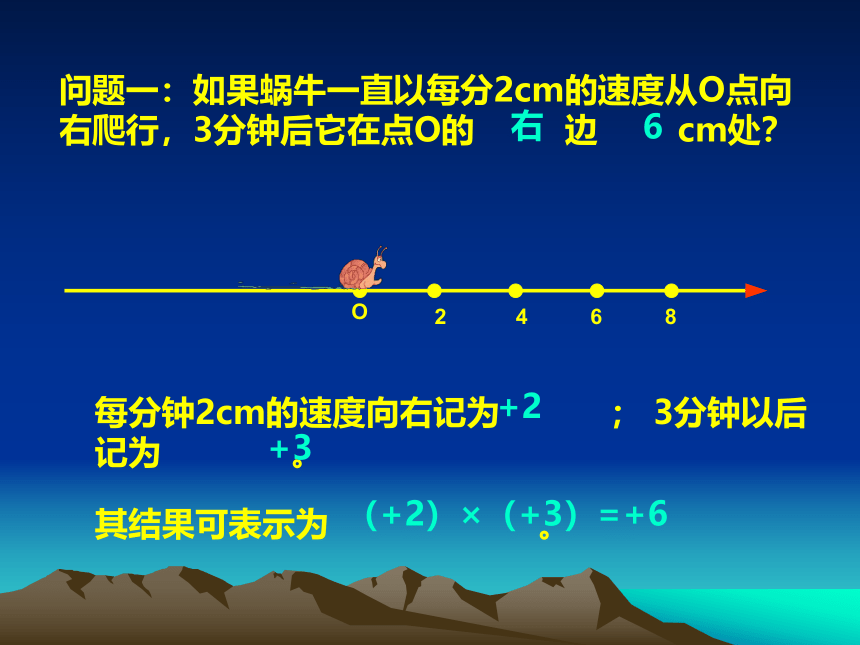
问题一:如果蜗牛一直以每分2cm的速度从O点向右爬行,3分钟后它在点O的
边
cm处?
每分钟2cm的速度向右记为
;
3分钟以后记为
。
其结果可表示为
。
右
6
+2
+3
(+2)×(+3)=+6
问题二:如果蜗牛一直以每分2cm的速度从O点向左爬行,3分钟后它在点O的
边
cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向左记为
;
3分钟以后记为
。
其结果可表示为
。
-2
+3
(-2)×(+3)=-6
想一想:
问题1的算式(+2)×(+3)=+6
与问题2的算式(-2)×(+3)=-6有何区别?
结论:
两个有理数相乘,改变其中一个因数的符号(绝对值不变),积的符号也随之改变。
问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在点O处,
3分钟前它在点O的
边
cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向右记为
;
3分钟以前记为
。
其结果可表示为
。
+2
-3
(+2)×(-3)=-6
比较问题3与问题1,你发现了什么?
问题四:
如果蜗牛一直以每分2cm的速度向
左爬行,现在蜗牛在点O处,
3分钟前它在点O
边
cm处?
O
2
4
6
8
右
6
每分钟2cm的速度向左记为
;
3分钟以前记为
。
其结果可表示为
。
-2
-3
(-2)×(-3)=+6
比较问题4与问题2,你发现了什么?
想一想:
问题1的算式(+2)×(+3)=+6
与问题4的算式(-2)×(-3)=+6有何区别?
问题2的算式(-2)×(+3)=-6
与问题3的算式(+2)×(-3)=-6
有何区别?
结论:
两个有理数相乘,同时改变两个因数的符号(绝对值不变),积的符号不变。
(+2)×(+3)
=
+6
(-2)×(+3)=
-6
(+2)×(-3)=
-6
(-2)×(-3)=
+6
正数乘以正数积为
数
负数乘以正数积为
数
正数乘以负数积为
数
负数乘以负数积为
数
乘积的绝对值等于各乘数绝对值的
。
规律呈现:
正
负
负
正
积
因数的符号相同,积为正。因数的符号不同,积为负
问题五:如果蜗牛一直以每分钟2cm的速度向右爬行,0分钟后它在什么位置?
O
2
4
6
8
问题六:如果蜗牛一直以每分钟0cm的速度向左爬行,3分钟前它在什么位置?
O
-8
-6
-4
-2
结论:
2×0=
0
结论:
0×(-3)=
0
一个数与0相乘,积为0.
归纳
有理数的乘法法则:
1、
两数相乘,同号得正,异号
得负,并把绝对值相乘。
2、任何数同零相乘,都得零。
自学例1
例如,
(-5)×(-3),……
(-5)×(-3)=
+(),……
5
×
3=15,…………
所以
(-5)×(-3)=15
又如,(-7)
×4,…………
(-7)
×4=
-(),……
7
×4=28,…………
所以
(-7)
×4=
有理数相乘,先确定积的
,
再确定积的
。
同号两数相乘
得正
把绝对值相乘
异号两数相乘
得负
把绝对值相乘
-28
符号
绝对值
把绝对值相乘
小试牛刀
(1)
6
×
(-
9)
(3)(-
6)×(-
1)
(4)(-
6)×
0
(2)(-
15)
×
(5)(-
12)×(-
)
(6)(+
2
)×(-
)
相信自己,你一定行!
定义:乘积是1的两个数互为倒数
1的倒数为
-1的倒数为
的倒数为
-
的倒数为
5的倒数为
-5的倒数为
的倒数为
-
的倒数为
1
-1
3
-3
-3
-3
做练习题2
商店降价销售某种商品,每件降5元,
售出60件后,与按原价销售同样数量
的商品相比,销售额有什么变化?
解:(-5)×60
=-300(元)
答:销售额减少300元。
再试牛刀
通过本节课的学习,大家有
什么收获呢?
作业:
1、习题A组第1题,第2题
2、习题B组第2题
3、预习多个有理数相乘的乘法运算
同学们
再见!
学习目标
1.理解有理数乘法法则,能利用有理数乘法法则计算两个数的乘法。
2.理解有理数倒数的意义,会求一个有理数的倒数。
3.能说出有理数乘法法则,能正确运用有理数乘法法则。
教学重、难点
重点:有理数乘法法则的应用,倒数的定义,并会求。
难点:有理数乘法法则的推导过程。
L
O
如图,有一只蜗牛沿直线L爬行,它现在的位置恰好在L
上的一点O。
1、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟后它在什么位置?
2、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
4、如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
3、如果蜗牛一直以每分钟2cm的速度向右爬行,3分钟前它在什么位置?
提出问题,导入新课
2、如果3分钟以后记为+3分钟,那么3分钟以前应该记为
。
1、如果一只蜗牛向右爬行2cm记为+2cm,那么向左爬行2cm应该记为
。
-2cm
-3分钟
O
2
4
6
8
问题一:如果蜗牛一直以每分2cm的速度从O点向右爬行,3分钟后它在点O的
边
cm处?
每分钟2cm的速度向右记为
;
3分钟以后记为
。
其结果可表示为
。
右
6
+2
+3
(+2)×(+3)=+6
问题二:如果蜗牛一直以每分2cm的速度从O点向左爬行,3分钟后它在点O的
边
cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向左记为
;
3分钟以后记为
。
其结果可表示为
。
-2
+3
(-2)×(+3)=-6
想一想:
问题1的算式(+2)×(+3)=+6
与问题2的算式(-2)×(+3)=-6有何区别?
结论:
两个有理数相乘,改变其中一个因数的符号(绝对值不变),积的符号也随之改变。
问题三:如果蜗牛一直以每分2cm的速度向右爬行,现在蜗牛在点O处,
3分钟前它在点O的
边
cm处?
O
-8
-6
-4
-2
左
6
每分钟2cm的速度向右记为
;
3分钟以前记为
。
其结果可表示为
。
+2
-3
(+2)×(-3)=-6
比较问题3与问题1,你发现了什么?
问题四:
如果蜗牛一直以每分2cm的速度向
左爬行,现在蜗牛在点O处,
3分钟前它在点O
边
cm处?
O
2
4
6
8
右
6
每分钟2cm的速度向左记为
;
3分钟以前记为
。
其结果可表示为
。
-2
-3
(-2)×(-3)=+6
比较问题4与问题2,你发现了什么?
想一想:
问题1的算式(+2)×(+3)=+6
与问题4的算式(-2)×(-3)=+6有何区别?
问题2的算式(-2)×(+3)=-6
与问题3的算式(+2)×(-3)=-6
有何区别?
结论:
两个有理数相乘,同时改变两个因数的符号(绝对值不变),积的符号不变。
(+2)×(+3)
=
+6
(-2)×(+3)=
-6
(+2)×(-3)=
-6
(-2)×(-3)=
+6
正数乘以正数积为
数
负数乘以正数积为
数
正数乘以负数积为
数
负数乘以负数积为
数
乘积的绝对值等于各乘数绝对值的
。
规律呈现:
正
负
负
正
积
因数的符号相同,积为正。因数的符号不同,积为负
问题五:如果蜗牛一直以每分钟2cm的速度向右爬行,0分钟后它在什么位置?
O
2
4
6
8
问题六:如果蜗牛一直以每分钟0cm的速度向左爬行,3分钟前它在什么位置?
O
-8
-6
-4
-2
结论:
2×0=
0
结论:
0×(-3)=
0
一个数与0相乘,积为0.
归纳
有理数的乘法法则:
1、
两数相乘,同号得正,异号
得负,并把绝对值相乘。
2、任何数同零相乘,都得零。
自学例1
例如,
(-5)×(-3),……
(-5)×(-3)=
+(),……
5
×
3=15,…………
所以
(-5)×(-3)=15
又如,(-7)
×4,…………
(-7)
×4=
-(),……
7
×4=28,…………
所以
(-7)
×4=
有理数相乘,先确定积的
,
再确定积的
。
同号两数相乘
得正
把绝对值相乘
异号两数相乘
得负
把绝对值相乘
-28
符号
绝对值
把绝对值相乘
小试牛刀
(1)
6
×
(-
9)
(3)(-
6)×(-
1)
(4)(-
6)×
0
(2)(-
15)
×
(5)(-
12)×(-
)
(6)(+
2
)×(-
)
相信自己,你一定行!
定义:乘积是1的两个数互为倒数
1的倒数为
-1的倒数为
的倒数为
-
的倒数为
5的倒数为
-5的倒数为
的倒数为
-
的倒数为
1
-1
3
-3
-3
-3
做练习题2
商店降价销售某种商品,每件降5元,
售出60件后,与按原价销售同样数量
的商品相比,销售额有什么变化?
解:(-5)×60
=-300(元)
答:销售额减少300元。
再试牛刀
通过本节课的学习,大家有
什么收获呢?
作业:
1、习题A组第1题,第2题
2、习题B组第2题
3、预习多个有理数相乘的乘法运算
同学们
再见!
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
