第13章立体几何初步单元测试题-2020-2021学年高一下学期数学苏教版(2019)必修第二册(Word含答案解析)
文档属性
| 名称 | 第13章立体几何初步单元测试题-2020-2021学年高一下学期数学苏教版(2019)必修第二册(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 604.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 22:01:10 | ||
图片预览




文档简介
立体几何初步
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出以下四个命题:
①不共面的四点中,其中任意三点不共线;
②若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
2.设l为直线,α,β是两个不同的平面.下列命题中正确的是( )
A.若l∥α,l∥β,则α∥β
B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β
D.若α⊥β,l∥α,则l⊥β
3.若把一个高为10
cm的圆柱的底面画在x′O′y′平面上,则圆柱的高应画成( )
A.平行于z′轴且大小为10
cm
B.平行于z′轴且大小为5
cm
C.与z′轴成45°且大小为10
cm
D.与z′轴成45°且大小为5
cm
4.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60°
B.45°
C.30°
D.120°
5.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )
A.πa2
B.πa2
C.πa2
D.5πa2
6.如图,PA⊥面ABC,∠ACB=90°,且PA=AC=BC=a,则异面直线PB与AC所成的角的正切值等于( )
A.2
B.
C.
D.
7.在正方体ABCD?A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E、F,则四边形D1EBF的形状是( )
A.矩形
B.菱形
C.平行四边形
D.正方形
8.如图,在边长为1的正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在的直线进行翻折,将△CDE沿DE所在的直线进行翻折,在翻折过程中,下列说法错误的是( )
A.无论翻折到什么位置,A、C两点都不可能重合
B.存在某个位置,使得直线AF与直线CE所成的角为60°
C.存在某个位置,使得直线AF与直线CE所成的角为90°
D.存在某个位置,使得直线AB与直线CD所成的角为90°
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列命题为真命题的是( )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
10.正方体ABCD?A1B1C1D1中,E为线段B1D1上的一个动点,则下列结论中正确的是( )
A.
AC⊥BE
B.
B1E∥平面ABCD
C.三棱锥E?ABC的体积为定值
D.B1E⊥BC1
11.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折的过程中,下列命题正确的是( )
A.BM是定值
B.点M在某个球面上运动
C.存在某个位置,使DE⊥A1C
D.存在某个位置,使MB∥平面A1DE
12.
在正方体ABCD?A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在BD1上且BP=BD1,则下面说法正确的是( )
A.MN∥平面APC
B.C1Q∥平面APC
C.A,P,M三点共线
D.平面MNQ∥平面APC
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.已知正六棱柱的侧面积为72
cm2,高为6
cm,那么它的体积为________cm3.
14.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的表面积为________,体积为________.(本题第一空2分,第二空3分)
15.棱长为1的正四面体内有一点P,由点P向各个面引垂线,垂线段分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为________.
16.已知棱长为的正方体ABCD?A1B1C1D1内有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为__________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图,正方体ABCD?A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
(1)三棱锥A′?BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′?BC′D的体积.
18.(本小题满分12分)如图,在三棱锥A?BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
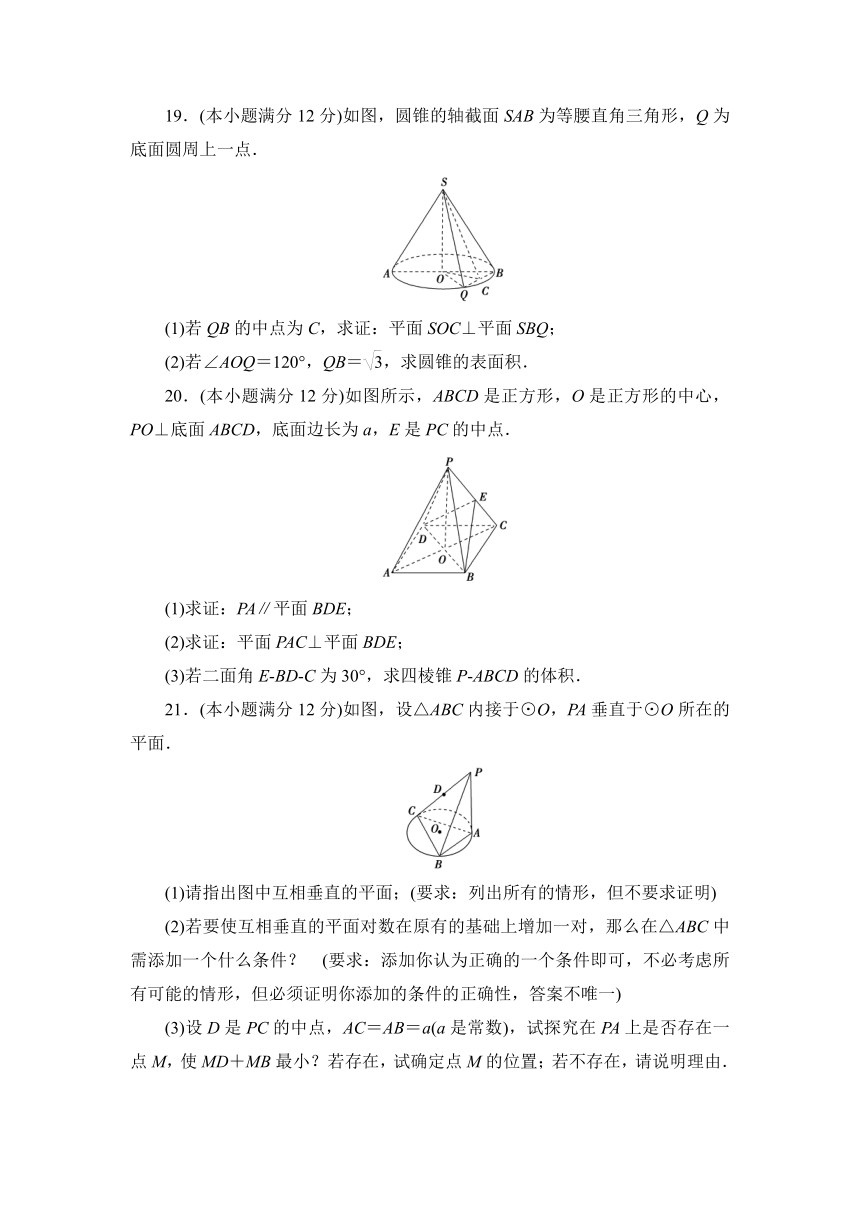
19.(本小题满分12分)如图,圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上一点.
(1)若QB的中点为C,求证:平面SOC⊥平面SBQ;
(2)若∠AOQ=120°,QB=,求圆锥的表面积.
20.(本小题满分12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:PA∥平面BDE;
(2)求证:平面PAC⊥平面BDE;
(3)若二面角E?BD?C为30°,求四棱锥P?ABCD的体积.
21.(本小题满分12分)如图,设△ABC内接于⊙O,PA垂直于⊙O所在的平面.
(1)请指出图中互相垂直的平面;(要求:列出所有的情形,但不要求证明)
(2)若要使互相垂直的平面对数在原有的基础上增加一对,那么在△ABC中需添加一个什么条件?
(要求:添加你认为正确的一个条件即可,不必考虑所有可能的情形,但必须证明你添加的条件的正确性,答案不唯一)
(3)设D是PC的中点,AC=AB=a(a是常数),试探究在PA上是否存在一点M,使MD+MB最小?若存在,试确定点M的位置;若不存在,请说明理由.
22.(本小题满分12分)如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1) (2)
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ.说明理由.
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出以下四个命题:
①不共面的四点中,其中任意三点不共线;
②若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
B [①假设其中有三点共线,则该直线和直线外的另一点确定一个平面,这与四点不共面矛盾,故其中任意三点不共线,所以①正确;②如图,两个相交平面有三个公共点A,B,C,但A,B,C,D,E不共面,所以②不正确;③显然不正确;④不正确.因为此时所得的四边形的四条边可以不在一个平面上,如空间四边形.]
2.设l为直线,α,β是两个不同的平面.下列命题中正确的是( )
A.若l∥α,l∥β,则α∥β
B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β
D.若α⊥β,l∥α,则l⊥β
B [对于A,若l∥α,l∥β,则α和β可能平行,也可能相交,故错误;
对于B,若l⊥α,l⊥β,则α∥β,故正确;
对于C,若l⊥α,l∥β,则α⊥β,故错误;
对于D,若α⊥β,l∥α,则l与β的位置关系有三种可能:l⊥β,l∥β,l?β,故错误.故选B.]
3.若把一个高为10
cm的圆柱的底面画在x′O′y′平面上,则圆柱的高应画成( )
A.平行于z′轴且大小为10
cm
B.平行于z′轴且大小为5
cm
C.与z′轴成45°且大小为10
cm
D.与z′轴成45°且大小为5
cm
A [平行于z轴(或在z轴上)的线段,在直观图中的方向和长度都与原来保持一致.]
4.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60°
B.45°
C.30°
D.120°
A [∠ABO即是斜线AB与平面α所成的角,在Rt△AOB中,AB=2BO,
所以cos∠ABO=,
即∠ABO=60°.]
5.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )
A.πa2
B.πa2
C.πa2
D.5πa2
B [由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为a.如图,P为三棱柱上底面的中心,O为球心,易知AP=×a=a,OP=a,所以球的半径R=OA满足R2=+=a2,故S球=4πR2=πa2.]
6.如图,PA⊥面ABC,∠ACB=90°,且PA=AC=BC=a,则异面直线PB与AC所成的角的正切值等于( )
A.2
B.
C.
D.
B [如图,将此多面体补成一个正方体,
因为AC∥BD,所以PB与AC所成角的大小即为此正方体体对角线PB与棱BD所成角的大小,
在Rt△PBD中,∠PDB=90°,PD=a,DB=a,
所以tan∠DBP==.故选B.]
7.在正方体ABCD?A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E、F,则四边形D1EBF的形状是( )
A.矩形
B.菱形
C.平行四边形
D.正方形
C [因为过D1B的平面和左右两个侧面分别交于ED1、BF,所以ED1∥BF,同理D1F∥EB,所以四边形D1EBF是平行四边形.]
8.如图,在边长为1的正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在的直线进行翻折,将△CDE沿DE所在的直线进行翻折,在翻折过程中,下列说法错误的是( )
A.无论翻折到什么位置,A、C两点都不可能重合
B.存在某个位置,使得直线AF与直线CE所成的角为60°
C.存在某个位置,使得直线AF与直线CE所成的角为90°
D.存在某个位置,使得直线AB与直线CD所成的角为90°
D [在A中,点A与点C一定不重合,故A正确;在B中,存在某个位置,使得直线AF与直线CE所成的角为60°,故B正确;在C中,当平面ABF⊥平面BEDF,平面DCE⊥平面BEDF时,直线AF与直线CE垂直,故C正确;在D中,直线AB与直线CD不可能垂直,故D错误.故选D.]
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列命题为真命题的是( )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
BD [两个平面相交时,也有无数个公共点,A错;比如a⊥α,b?α,c?α,显然有a⊥b,a⊥c,但b与c也可能相交,C错.故选BD.
]
10.正方体ABCD?A1B1C1D1中,E为线段B1D1上的一个动点,则下列结论中正确的是( )
A.
AC⊥BE
B.
B1E∥平面ABCD
C.三棱锥E?ABC的体积为定值
D.B1E⊥BC1
ABC [因为AC⊥平面BDD1B1,故A正确;因为B1D1∥平面ABCD,故B正确;记正方体的体积为V,
则VE?ABC=V,为定值,故C正确;B1E与BC1不垂直,故D错误.故选ABC.]
11.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折的过程中,下列命题正确的是( )
A.BM是定值
B.点M在某个球面上运动
C.存在某个位置,使DE⊥A1C
D.存在某个位置,使MB∥平面A1DE
ABD [取DC的中点F,连接MF,BF,MF∥A1D且MF=A1D,FB∥ED且FB=ED,所以∠MFB=∠A1DE,由余弦定理可得MB2=MF2+FB2-2MF·FB·cos
∠MFB是定值;因为B是定点,所以M是在以B为圆心,MB为半径的球面上,可得A,B正确;由MF∥A1D与FB∥ED且MF∩BF=F可得平面MBF∥平面A1DE,故D正确;A1C在平面ABCD中的投影与AC重合,AC与DE不垂直,所以DE与A1C也不垂直,故C不正确.]
12.
在正方体ABCD?A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在BD1上且BP=BD1,则下面说法正确的是( )
A.MN∥平面APC
B.C1Q∥平面APC
C.A,P,M三点共线
D.平面MNQ∥平面APC
BC [如图,对于A,连接MN,AC,则MN∥AC,连接AM,CN,
易得AM,CN交于点P,即MN?平面APC,所以MN∥平面APC是错误的.
对于B,由①知M,N在平面APC内,由题易知AN∥C1Q,且AN?平面APC,
C1Q?平面APC.
所以C1Q∥平面APC是正确的.
对于C,由①知,A,P,M三点共线是正确的.
对于D,由①知MN?平面APC,又MN?平面MNQ,所以平面MNQ∥平面APC是错误的.故选BC.]
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.已知正六棱柱的侧面积为72
cm2,高为6
cm,那么它的体积为________cm3.
36 [设正六棱柱的底面边长为x
cm,由题意得6x·6=72,所以x=2,
于是其体积V=×22×6×6=36
cm3.]
14.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的表面积为________,体积为________.(本题第一空2分,第二空3分)
3π π [设圆锥的底面半径为r,根据题意,得2πr=2π,解得r=1,根据勾股定理,得圆锥的高为=,所以圆锥的表面积S=×π×22+π×12=3π,
体积V=×π×12×=π.]
15.棱长为1的正四面体内有一点P,由点P向各个面引垂线,垂线段分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为________.
[设四面体的高为h,
则h=eq
\r(12-\b\lc\(\rc\)(\a\vs4\al\co1(\f(2,3)×\f(\r(3),2)×1)))=,
Sh=S(d1+d2+d3+d4),
∴d1+d2+d3+d4=h=.]
16.已知棱长为的正方体ABCD?A1B1C1D1内有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为__________.
[由题意知,只需考虑圆柱的底面与正方体的表面相切的情况,由图形的对称性可知,侧面积最大时,圆柱的上底面必与过A点的三个面相切,且切点分别在线段AB1,AC,AD1上,如图所示,设线段AB1上的切点为E,AC1与平面A1BD的交点为O2,圆柱上底面的圆心为O1,半径即为O1E,记为r,设
AB1与平面A1BD的交点为F.
∵正方体ABCD?A1B1C1D1的棱长为,∴AC1=3,A1B=BD=A1D=.
由题意知,O2F=DF=××=,AO2=AC1=1.
由O1E∥O2F知=,
∴AO1=O1E,则圆柱的高为3-2AO1=3-2r,
S侧=2πr(3-2r)=4π
=-4π+≤,
当r=时,圆柱的侧面积取得最大值,最大值为.]
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图,正方体ABCD?A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
(1)三棱锥A′?BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′?BC′D的体积.
[解] (1)∵ABCD?A′B′C′D′是正方体,
∴六个面是互相全等的正方形,
∴A′C′=A′B=A′D=BC′=BD=C′D=a,
∴S三棱锥=4××(a)2=2a2,S正方体=6a2,
∴=.
(2)显然,三棱锥A′?ABD,C′?BCD,D?A′D′C′,
B?A′B′C′是完全一样的,
∴V三棱锥A′?BC′D=V正方体-4V三棱锥A′?ABD
=a3-4××a2×a=a3.
18.(本小题满分12分)如图,在三棱锥A?BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
[证明] (1)在平面ABD内,因为AB⊥AD,EF⊥AD,
所以EF∥AB.
又因为EF?平面ABC,AB?平面ABC,
所以EF∥平面ABC.
(2)因为平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,
BC?平面BCD,BC⊥BD,
所以BC⊥平面ABD.
因为AD?平面ABD,所以BC⊥AD.
又AB⊥AD,BC∩AB=B,AB?平面ABC,BC?平面ABC,
所以AD⊥平面ABC.
又因为AC?平面ABC,所以AD⊥AC.
19.(本小题满分12分)如图,圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上一点.
(1)若QB的中点为C,求证:平面SOC⊥平面SBQ;
(2)若∠AOQ=120°,QB=,求圆锥的表面积.
[解] (1)证明:∵SQ=SB,OQ=OB,C为QB的中点,
∴QB⊥SC,QB⊥OC.
∵SC∩OC=C,∴QB⊥平面SOC.
又∵QB?平面SBQ,
∴平面SOC⊥平面SBQ.
(2)∵∠AOQ=120°,QB=,
∴∠BOQ=60°,即△OBQ为等边三角形,∴OB=.
∵△SAB为等腰直角三角形,∴SB=,
∴S侧=×π=3π,
∴S表=S侧+S底=3π+3π=(3+3)π.
20.(本小题满分12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:PA∥平面BDE;
(2)求证:平面PAC⊥平面BDE;
(3)若二面角E?BD?C为30°,求四棱锥P?ABCD的体积.
[解] (1)证明:连接OE,如图所示.
∵O,E分别为AC,PC的中点,
∴OE∥PA.
∵OE?平面BDE,PA?平面BDE,∴PA∥平面BDE.
(2)证明:∵PO⊥平面ABCD,
∴PO⊥BD.
在正方形ABCD中,BD⊥AC.
又∵PO∩AC=O,∴BD⊥平面PAC.
又∵BD?平面BDE,∴平面PAC⊥平面BDE.
(3)取OC中点F,连接EF.∵E为PC中点,
∴EF为△POC的中位线,∴EF∥PO.
又∵PO⊥平面ABCD,∴EF⊥平面ABCD,
∴EF⊥BD.
∵OF⊥BD,OF∩EF=F,∴BD⊥平面EFO,
∴OE⊥BD,∴∠EOF为二面角E?BD?C的平面角,
∴∠EOF=30°.
在Rt△OEF中,OF=OC=AC=a,
∴EF=OF·tan
30°=a,∴OP=2EF=a.
∴VP?ABCD=×a2×a=a3.
21.(本小题满分12分)如图,设△ABC内接于⊙O,PA垂直于⊙O所在的平面.
(1)请指出图中互相垂直的平面;(要求:列出所有的情形,但不要求证明)
(2)若要使互相垂直的平面对数在原有的基础上增加一对,那么在△ABC中需添加一个什么条件?
(要求:添加你认为正确的一个条件即可,不必考虑所有可能的情形,但必须证明你添加的条件的正确性,答案不唯一)
(3)设D是PC的中点,AC=AB=a(a是常数),试探究在PA上是否存在一点M,使MD+MB最小?若存在,试确定点M的位置;若不存在,请说明理由.
[解] (1)图中互相垂直的平面有:
平面PAC⊥平面ABC,平面PAB⊥平面ABC.
(2)要使互相垂直的平面对数在原有的基础上增加一对,在△ABC中需添加AB⊥BC(或AC是圆O的直径).
证明如下:
∵PA⊥平面ABC,BC?平面ABC,
∴BC⊥PA,
∵AB⊥BC,PA∩AB=A,
∴BC⊥平面PAB,
又BC?平面PBC,∴平面PBC⊥平面PAB;
(3)将平面PAB绕PA沿逆时针方向旋转到与平面PAC在同一平面上,
如图,
∵PA⊥AC,PA⊥AB,
∴C、A、B在同一条直线上,连接DB交PA于点M,则点M就是所求的点,过点D作DE∥BC,交PA于E,
∵D是PC的中点,∴E是PA的中点,
∵=,且AC=AB,∴=2,
∴AM=AE=AP,即M为AP上靠近点A的一个三等分点时,MD+MB最小.
22.(本小题满分12分)如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1) (2)
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ.说明理由.
[解] (1)证明:∵D,E分别为AC,AB的中点,
∴DE∥BC.
又∵DE?平面A1CB,BC?平面A1CB,
∴DE∥平面A1CB.
(2)证明:由已知得AC⊥BC且DE∥BC,
∴DE⊥AC,
∴DE⊥A1D,DE⊥CD,
又A1D∩CD=D,
∴DE⊥平面A1DC,而A1F?平面A1DC,
∴DE⊥A1F.
又∵A1F⊥CD,DE∩CD=D,
∴A1F⊥平面BCDE,
∵BE?平面BCDE,
∴A1F⊥BE.
(3)线段A1B上存在点Q,使A1C⊥平面DEQ.
理由如下:
如图,分别取A1C,A1B的中点P,Q,连接PQ,QE,PD,则PQ∥BC.
又∵DE∥BC,
∴DE∥PQ,
∴平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,A1C?平面A1DC,
∴DE⊥A1C.
又∵P是等腰三角形DA1C底边A1C的中点,
∴A1C⊥DP.
又DE∩DP=D,
∴A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q(A1B的中点),使得A1C⊥平面DEQ.
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出以下四个命题:
①不共面的四点中,其中任意三点不共线;
②若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
2.设l为直线,α,β是两个不同的平面.下列命题中正确的是( )
A.若l∥α,l∥β,则α∥β
B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β
D.若α⊥β,l∥α,则l⊥β
3.若把一个高为10
cm的圆柱的底面画在x′O′y′平面上,则圆柱的高应画成( )
A.平行于z′轴且大小为10
cm
B.平行于z′轴且大小为5
cm
C.与z′轴成45°且大小为10
cm
D.与z′轴成45°且大小为5
cm
4.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60°
B.45°
C.30°
D.120°
5.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )
A.πa2
B.πa2
C.πa2
D.5πa2
6.如图,PA⊥面ABC,∠ACB=90°,且PA=AC=BC=a,则异面直线PB与AC所成的角的正切值等于( )
A.2
B.
C.
D.
7.在正方体ABCD?A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E、F,则四边形D1EBF的形状是( )
A.矩形
B.菱形
C.平行四边形
D.正方形
8.如图,在边长为1的正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在的直线进行翻折,将△CDE沿DE所在的直线进行翻折,在翻折过程中,下列说法错误的是( )
A.无论翻折到什么位置,A、C两点都不可能重合
B.存在某个位置,使得直线AF与直线CE所成的角为60°
C.存在某个位置,使得直线AF与直线CE所成的角为90°
D.存在某个位置,使得直线AB与直线CD所成的角为90°
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列命题为真命题的是( )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
10.正方体ABCD?A1B1C1D1中,E为线段B1D1上的一个动点,则下列结论中正确的是( )
A.
AC⊥BE
B.
B1E∥平面ABCD
C.三棱锥E?ABC的体积为定值
D.B1E⊥BC1
11.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折的过程中,下列命题正确的是( )
A.BM是定值
B.点M在某个球面上运动
C.存在某个位置,使DE⊥A1C
D.存在某个位置,使MB∥平面A1DE
12.
在正方体ABCD?A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在BD1上且BP=BD1,则下面说法正确的是( )
A.MN∥平面APC
B.C1Q∥平面APC
C.A,P,M三点共线
D.平面MNQ∥平面APC
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.已知正六棱柱的侧面积为72
cm2,高为6
cm,那么它的体积为________cm3.
14.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的表面积为________,体积为________.(本题第一空2分,第二空3分)
15.棱长为1的正四面体内有一点P,由点P向各个面引垂线,垂线段分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为________.
16.已知棱长为的正方体ABCD?A1B1C1D1内有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为__________.
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图,正方体ABCD?A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
(1)三棱锥A′?BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′?BC′D的体积.
18.(本小题满分12分)如图,在三棱锥A?BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
19.(本小题满分12分)如图,圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上一点.
(1)若QB的中点为C,求证:平面SOC⊥平面SBQ;
(2)若∠AOQ=120°,QB=,求圆锥的表面积.
20.(本小题满分12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:PA∥平面BDE;
(2)求证:平面PAC⊥平面BDE;
(3)若二面角E?BD?C为30°,求四棱锥P?ABCD的体积.
21.(本小题满分12分)如图,设△ABC内接于⊙O,PA垂直于⊙O所在的平面.
(1)请指出图中互相垂直的平面;(要求:列出所有的情形,但不要求证明)
(2)若要使互相垂直的平面对数在原有的基础上增加一对,那么在△ABC中需添加一个什么条件?
(要求:添加你认为正确的一个条件即可,不必考虑所有可能的情形,但必须证明你添加的条件的正确性,答案不唯一)
(3)设D是PC的中点,AC=AB=a(a是常数),试探究在PA上是否存在一点M,使MD+MB最小?若存在,试确定点M的位置;若不存在,请说明理由.
22.(本小题满分12分)如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1) (2)
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ.说明理由.
一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.给出以下四个命题:
①不共面的四点中,其中任意三点不共线;
②若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面;
③若直线a,b共面,直线a,c共面,则直线b,c共面;
④依次首尾相接的四条线段必共面.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
B [①假设其中有三点共线,则该直线和直线外的另一点确定一个平面,这与四点不共面矛盾,故其中任意三点不共线,所以①正确;②如图,两个相交平面有三个公共点A,B,C,但A,B,C,D,E不共面,所以②不正确;③显然不正确;④不正确.因为此时所得的四边形的四条边可以不在一个平面上,如空间四边形.]
2.设l为直线,α,β是两个不同的平面.下列命题中正确的是( )
A.若l∥α,l∥β,则α∥β
B.若l⊥α,l⊥β,则α∥β
C.若l⊥α,l∥β,则α∥β
D.若α⊥β,l∥α,则l⊥β
B [对于A,若l∥α,l∥β,则α和β可能平行,也可能相交,故错误;
对于B,若l⊥α,l⊥β,则α∥β,故正确;
对于C,若l⊥α,l∥β,则α⊥β,故错误;
对于D,若α⊥β,l∥α,则l与β的位置关系有三种可能:l⊥β,l∥β,l?β,故错误.故选B.]
3.若把一个高为10
cm的圆柱的底面画在x′O′y′平面上,则圆柱的高应画成( )
A.平行于z′轴且大小为10
cm
B.平行于z′轴且大小为5
cm
C.与z′轴成45°且大小为10
cm
D.与z′轴成45°且大小为5
cm
A [平行于z轴(或在z轴上)的线段,在直观图中的方向和长度都与原来保持一致.]
4.如图所示,若斜线段AB是它在平面α上的射影BO的2倍,则AB与平面α所成的角是( )
A.60°
B.45°
C.30°
D.120°
A [∠ABO即是斜线AB与平面α所成的角,在Rt△AOB中,AB=2BO,
所以cos∠ABO=,
即∠ABO=60°.]
5.设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )
A.πa2
B.πa2
C.πa2
D.5πa2
B [由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为a.如图,P为三棱柱上底面的中心,O为球心,易知AP=×a=a,OP=a,所以球的半径R=OA满足R2=+=a2,故S球=4πR2=πa2.]
6.如图,PA⊥面ABC,∠ACB=90°,且PA=AC=BC=a,则异面直线PB与AC所成的角的正切值等于( )
A.2
B.
C.
D.
B [如图,将此多面体补成一个正方体,
因为AC∥BD,所以PB与AC所成角的大小即为此正方体体对角线PB与棱BD所成角的大小,
在Rt△PBD中,∠PDB=90°,PD=a,DB=a,
所以tan∠DBP==.故选B.]
7.在正方体ABCD?A1B1C1D1中,若经过D1B的平面分别交AA1和CC1于点E、F,则四边形D1EBF的形状是( )
A.矩形
B.菱形
C.平行四边形
D.正方形
C [因为过D1B的平面和左右两个侧面分别交于ED1、BF,所以ED1∥BF,同理D1F∥EB,所以四边形D1EBF是平行四边形.]
8.如图,在边长为1的正方形ABCD中,点E,F分别为边BC,AD的中点,将△ABF沿BF所在的直线进行翻折,将△CDE沿DE所在的直线进行翻折,在翻折过程中,下列说法错误的是( )
A.无论翻折到什么位置,A、C两点都不可能重合
B.存在某个位置,使得直线AF与直线CE所成的角为60°
C.存在某个位置,使得直线AF与直线CE所成的角为90°
D.存在某个位置,使得直线AB与直线CD所成的角为90°
D [在A中,点A与点C一定不重合,故A正确;在B中,存在某个位置,使得直线AF与直线CE所成的角为60°,故B正确;在C中,当平面ABF⊥平面BEDF,平面DCE⊥平面BEDF时,直线AF与直线CE垂直,故C正确;在D中,直线AB与直线CD不可能垂直,故D错误.故选D.]
二、选择题(本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求的,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列命题为真命题的是( )
A.若两个平面有无数个公共点,则这两个平面重合
B.若一个平面经过另一个平面的垂线,那么这两个平面相互垂直
C.垂直于同一条直线的两条直线相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面不垂直
BD [两个平面相交时,也有无数个公共点,A错;比如a⊥α,b?α,c?α,显然有a⊥b,a⊥c,但b与c也可能相交,C错.故选BD.
]
10.正方体ABCD?A1B1C1D1中,E为线段B1D1上的一个动点,则下列结论中正确的是( )
A.
AC⊥BE
B.
B1E∥平面ABCD
C.三棱锥E?ABC的体积为定值
D.B1E⊥BC1
ABC [因为AC⊥平面BDD1B1,故A正确;因为B1D1∥平面ABCD,故B正确;记正方体的体积为V,
则VE?ABC=V,为定值,故C正确;B1E与BC1不垂直,故D错误.故选ABC.]
11.如图,矩形ABCD中,AB=2AD,E为边AB的中点,将△ADE沿直线DE翻折成△A1DE.若M为线段A1C的中点,则在△ADE翻折的过程中,下列命题正确的是( )
A.BM是定值
B.点M在某个球面上运动
C.存在某个位置,使DE⊥A1C
D.存在某个位置,使MB∥平面A1DE
ABD [取DC的中点F,连接MF,BF,MF∥A1D且MF=A1D,FB∥ED且FB=ED,所以∠MFB=∠A1DE,由余弦定理可得MB2=MF2+FB2-2MF·FB·cos
∠MFB是定值;因为B是定点,所以M是在以B为圆心,MB为半径的球面上,可得A,B正确;由MF∥A1D与FB∥ED且MF∩BF=F可得平面MBF∥平面A1DE,故D正确;A1C在平面ABCD中的投影与AC重合,AC与DE不垂直,所以DE与A1C也不垂直,故C不正确.]
12.
在正方体ABCD?A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,点P在BD1上且BP=BD1,则下面说法正确的是( )
A.MN∥平面APC
B.C1Q∥平面APC
C.A,P,M三点共线
D.平面MNQ∥平面APC
BC [如图,对于A,连接MN,AC,则MN∥AC,连接AM,CN,
易得AM,CN交于点P,即MN?平面APC,所以MN∥平面APC是错误的.
对于B,由①知M,N在平面APC内,由题易知AN∥C1Q,且AN?平面APC,
C1Q?平面APC.
所以C1Q∥平面APC是正确的.
对于C,由①知,A,P,M三点共线是正确的.
对于D,由①知MN?平面APC,又MN?平面MNQ,所以平面MNQ∥平面APC是错误的.故选BC.]
三、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上)
13.已知正六棱柱的侧面积为72
cm2,高为6
cm,那么它的体积为________cm3.
36 [设正六棱柱的底面边长为x
cm,由题意得6x·6=72,所以x=2,
于是其体积V=×22×6×6=36
cm3.]
14.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的表面积为________,体积为________.(本题第一空2分,第二空3分)
3π π [设圆锥的底面半径为r,根据题意,得2πr=2π,解得r=1,根据勾股定理,得圆锥的高为=,所以圆锥的表面积S=×π×22+π×12=3π,
体积V=×π×12×=π.]
15.棱长为1的正四面体内有一点P,由点P向各个面引垂线,垂线段分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为________.
[设四面体的高为h,
则h=eq
\r(12-\b\lc\(\rc\)(\a\vs4\al\co1(\f(2,3)×\f(\r(3),2)×1)))=,
Sh=S(d1+d2+d3+d4),
∴d1+d2+d3+d4=h=.]
16.已知棱长为的正方体ABCD?A1B1C1D1内有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为__________.
[由题意知,只需考虑圆柱的底面与正方体的表面相切的情况,由图形的对称性可知,侧面积最大时,圆柱的上底面必与过A点的三个面相切,且切点分别在线段AB1,AC,AD1上,如图所示,设线段AB1上的切点为E,AC1与平面A1BD的交点为O2,圆柱上底面的圆心为O1,半径即为O1E,记为r,设
AB1与平面A1BD的交点为F.
∵正方体ABCD?A1B1C1D1的棱长为,∴AC1=3,A1B=BD=A1D=.
由题意知,O2F=DF=××=,AO2=AC1=1.
由O1E∥O2F知=,
∴AO1=O1E,则圆柱的高为3-2AO1=3-2r,
S侧=2πr(3-2r)=4π
=-4π+≤,
当r=时,圆柱的侧面积取得最大值,最大值为.]
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图,正方体ABCD?A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
(1)三棱锥A′?BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′?BC′D的体积.
[解] (1)∵ABCD?A′B′C′D′是正方体,
∴六个面是互相全等的正方形,
∴A′C′=A′B=A′D=BC′=BD=C′D=a,
∴S三棱锥=4××(a)2=2a2,S正方体=6a2,
∴=.
(2)显然,三棱锥A′?ABD,C′?BCD,D?A′D′C′,
B?A′B′C′是完全一样的,
∴V三棱锥A′?BC′D=V正方体-4V三棱锥A′?ABD
=a3-4××a2×a=a3.
18.(本小题满分12分)如图,在三棱锥A?BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(1)EF∥平面ABC;
(2)AD⊥AC.
[证明] (1)在平面ABD内,因为AB⊥AD,EF⊥AD,
所以EF∥AB.
又因为EF?平面ABC,AB?平面ABC,
所以EF∥平面ABC.
(2)因为平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,
BC?平面BCD,BC⊥BD,
所以BC⊥平面ABD.
因为AD?平面ABD,所以BC⊥AD.
又AB⊥AD,BC∩AB=B,AB?平面ABC,BC?平面ABC,
所以AD⊥平面ABC.
又因为AC?平面ABC,所以AD⊥AC.
19.(本小题满分12分)如图,圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上一点.
(1)若QB的中点为C,求证:平面SOC⊥平面SBQ;
(2)若∠AOQ=120°,QB=,求圆锥的表面积.
[解] (1)证明:∵SQ=SB,OQ=OB,C为QB的中点,
∴QB⊥SC,QB⊥OC.
∵SC∩OC=C,∴QB⊥平面SOC.
又∵QB?平面SBQ,
∴平面SOC⊥平面SBQ.
(2)∵∠AOQ=120°,QB=,
∴∠BOQ=60°,即△OBQ为等边三角形,∴OB=.
∵△SAB为等腰直角三角形,∴SB=,
∴S侧=×π=3π,
∴S表=S侧+S底=3π+3π=(3+3)π.
20.(本小题满分12分)如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(1)求证:PA∥平面BDE;
(2)求证:平面PAC⊥平面BDE;
(3)若二面角E?BD?C为30°,求四棱锥P?ABCD的体积.
[解] (1)证明:连接OE,如图所示.
∵O,E分别为AC,PC的中点,
∴OE∥PA.
∵OE?平面BDE,PA?平面BDE,∴PA∥平面BDE.
(2)证明:∵PO⊥平面ABCD,
∴PO⊥BD.
在正方形ABCD中,BD⊥AC.
又∵PO∩AC=O,∴BD⊥平面PAC.
又∵BD?平面BDE,∴平面PAC⊥平面BDE.
(3)取OC中点F,连接EF.∵E为PC中点,
∴EF为△POC的中位线,∴EF∥PO.
又∵PO⊥平面ABCD,∴EF⊥平面ABCD,
∴EF⊥BD.
∵OF⊥BD,OF∩EF=F,∴BD⊥平面EFO,
∴OE⊥BD,∴∠EOF为二面角E?BD?C的平面角,
∴∠EOF=30°.
在Rt△OEF中,OF=OC=AC=a,
∴EF=OF·tan
30°=a,∴OP=2EF=a.
∴VP?ABCD=×a2×a=a3.
21.(本小题满分12分)如图,设△ABC内接于⊙O,PA垂直于⊙O所在的平面.
(1)请指出图中互相垂直的平面;(要求:列出所有的情形,但不要求证明)
(2)若要使互相垂直的平面对数在原有的基础上增加一对,那么在△ABC中需添加一个什么条件?
(要求:添加你认为正确的一个条件即可,不必考虑所有可能的情形,但必须证明你添加的条件的正确性,答案不唯一)
(3)设D是PC的中点,AC=AB=a(a是常数),试探究在PA上是否存在一点M,使MD+MB最小?若存在,试确定点M的位置;若不存在,请说明理由.
[解] (1)图中互相垂直的平面有:
平面PAC⊥平面ABC,平面PAB⊥平面ABC.
(2)要使互相垂直的平面对数在原有的基础上增加一对,在△ABC中需添加AB⊥BC(或AC是圆O的直径).
证明如下:
∵PA⊥平面ABC,BC?平面ABC,
∴BC⊥PA,
∵AB⊥BC,PA∩AB=A,
∴BC⊥平面PAB,
又BC?平面PBC,∴平面PBC⊥平面PAB;
(3)将平面PAB绕PA沿逆时针方向旋转到与平面PAC在同一平面上,
如图,
∵PA⊥AC,PA⊥AB,
∴C、A、B在同一条直线上,连接DB交PA于点M,则点M就是所求的点,过点D作DE∥BC,交PA于E,
∵D是PC的中点,∴E是PA的中点,
∵=,且AC=AB,∴=2,
∴AM=AE=AP,即M为AP上靠近点A的一个三等分点时,MD+MB最小.
22.(本小题满分12分)如图(1),在Rt△ABC中,∠C=90°,D,E分别为AC,AB的中点,点F为线段CD上的一点,将△ADE沿DE折起到△A1DE的位置,使A1F⊥CD,如图(2).
(1) (2)
(1)求证:DE∥平面A1CB;
(2)求证:A1F⊥BE;
(3)线段A1B上是否存在点Q,使A1C⊥平面DEQ.说明理由.
[解] (1)证明:∵D,E分别为AC,AB的中点,
∴DE∥BC.
又∵DE?平面A1CB,BC?平面A1CB,
∴DE∥平面A1CB.
(2)证明:由已知得AC⊥BC且DE∥BC,
∴DE⊥AC,
∴DE⊥A1D,DE⊥CD,
又A1D∩CD=D,
∴DE⊥平面A1DC,而A1F?平面A1DC,
∴DE⊥A1F.
又∵A1F⊥CD,DE∩CD=D,
∴A1F⊥平面BCDE,
∵BE?平面BCDE,
∴A1F⊥BE.
(3)线段A1B上存在点Q,使A1C⊥平面DEQ.
理由如下:
如图,分别取A1C,A1B的中点P,Q,连接PQ,QE,PD,则PQ∥BC.
又∵DE∥BC,
∴DE∥PQ,
∴平面DEQ即为平面DEP.
由(2)知,DE⊥平面A1DC,A1C?平面A1DC,
∴DE⊥A1C.
又∵P是等腰三角形DA1C底边A1C的中点,
∴A1C⊥DP.
又DE∩DP=D,
∴A1C⊥平面DEP.
从而A1C⊥平面DEQ.
故线段A1B上存在点Q(A1B的中点),使得A1C⊥平面DEQ.
同课章节目录
- 第9章 平面向量
- 9.1 向量概念
- 9.2 向量运算
- 9.3 向量基本定理及坐标表示
- 9.4 向量应用
- 第10章 三角恒等变换
- 10.1 两角和与差的三角函数
- 10.2 二倍角的三角函数
- 10.3 几个三角恒等式
- 第11章 解三角形
- 11.1 余弦定理
- 11.2 正弦定理
- 11.3 余弦定理、正弦定理的应用
- 第12章 复数
- 12.1 复数的概念
- 12.2 复数的运算
- 12.3 复数的几何意义
- 12.4 复数的三角形式
- 第13章 立体几何初步
- 13.1 基本立体图形
- 13.2 基本图形位置关系
- 13.3 空间图形的表面积和体积
- 第14章 统计
- 14.1 获取数据的基本途径及相关概念
- 14.2 抽样
- 14.3 统计图表
- 14.4 用样本估计总体
- 第15章 概率
- 15.1 随机事件和样本空间
- 15.2 随机事件的概率
- 15.3 互斥事件和独立事件
