华师大版数学七年级上册 5.2.3 平行线的性质 学案+当堂检测(含答案)
文档属性
| 名称 | 华师大版数学七年级上册 5.2.3 平行线的性质 学案+当堂检测(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 344.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 17:40:26 | ||
图片预览


文档简介
3.
平行线的性质
学习目标:
1.掌握两直线平行,同位角、内错角相等,同旁内角互补,并能熟练运用(重点);
2.能够根据平行线的性质进行简单的推理(难点).
自主学习
一、知识链接
平行线的判定方法有哪几种?
二、新知预习
(预习课本P175-177)完成下列各题:
1.两条平行线被第三条直线所截,同位角相等,简单地说,就是
;
2.两条平行线被第三条直线所截,内错角相等,简单地说,就是
;
3.两条平行线被第三条直线所截,同旁内角互补,简单地说,就是
.
练习:如图,若AB平行CD,则有:
(1)∠3
∠5,理由是
;
(2)∠2
∠4,理由是
;
(3)∠1+∠4=
°,理由是
.
合作探究
要点探究
探究点1:平行线的性质
问题1:画两条平行线a,b,然后画一条截线c与a,b相交,标出如图所示的角.
度量所形成的8个角的度数,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
观察:
∠1~
∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想.
猜想
:两条平行线被第三条直线所截,同位角
.
思考:再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?
【要点归纳】两条平行线被第三条直线所截,同位角相等.即两直线平行,同位角相等.
问题2:如图,已知a//b,那么∠2与∠3相等吗?为什么?
问题3:如图,已知a//b,那么∠2与∠4有什么关系呢?为什么?
【要点归纳】1.两条平行线被第三条直线所截,内错角相等.即:两直线平行,内错角相等.
2.两条平行线被第三条直线所截,同旁内角互补.即:两直线平行,同旁内角互补.
例1
如图,已知AB∥CD,∠1=50°,求∠2的度数.
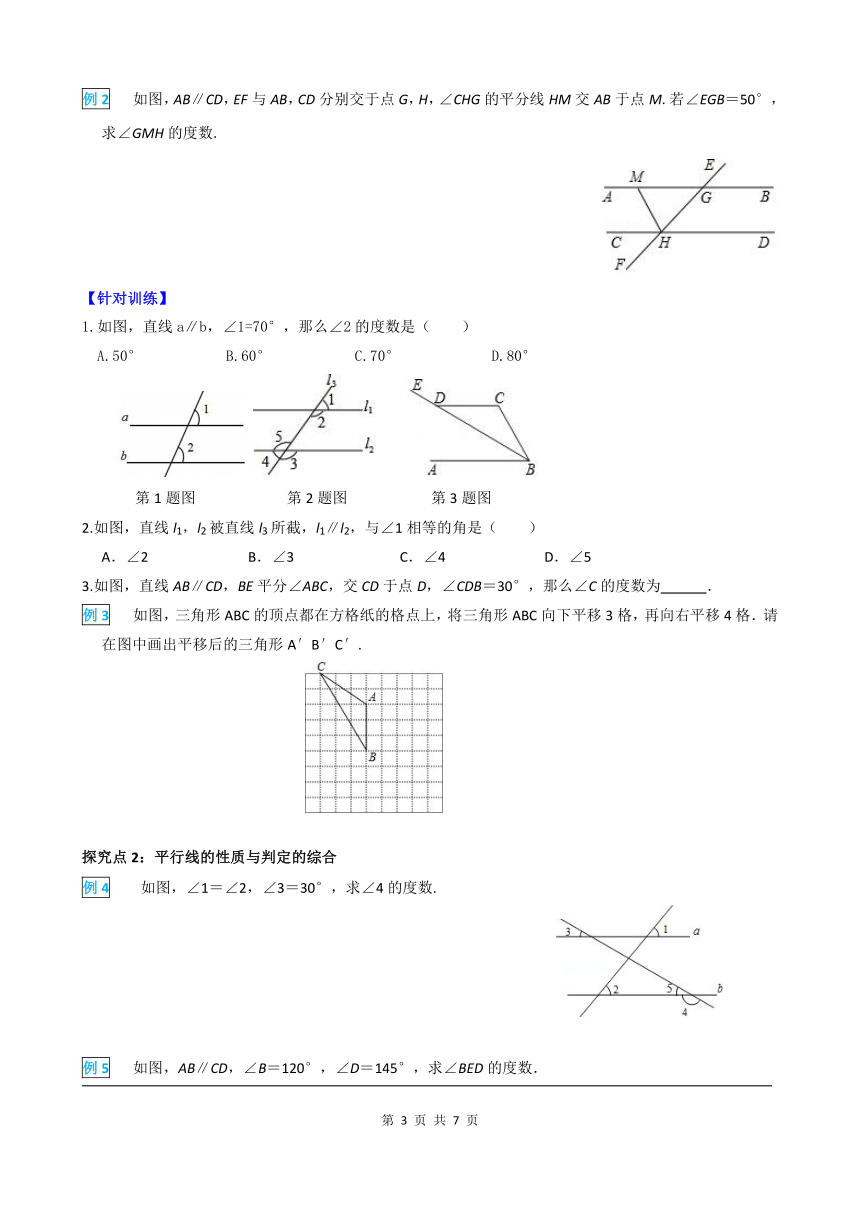
例2
如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M.若∠EGB=50°,求∠GMH的度数.
【针对训练】
1.如图,直线a∥b,∠1=70°,那么∠2的度数是(
)
A.50°
B.60°
C.70°
D.80°
第1题图
第2题图
第3题图
2.如图,直线l1,l2被直线l3所截,l1∥l2,与∠1相等的角是( )
A.∠2
B.∠3
C.∠4
D.∠5
3.如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为
.
例3
如图,三角形ABC的顶点都在方格纸的格点上,将三角形ABC向下平移3格,再向右平移4格.请在图中画出平移后的三角形A′B′C′.
探究点2:平行线的性质与判定的综合
例4
如图,∠1=∠2,∠3=30°,求∠4的度数.
例5
如图,AB∥CD,∠B=120°,∠D=145°,求∠BED的度数.
二、课堂小结
当堂检测
1.如图,直线a、b被直线c所截,a∥b,∠2=48°,则∠1的度数为( )
A.48°
B.58°
C.132°
D.122°
第1题图
第2题图
2.如图,已知a∥b,得到∠1+∠2=180°的依据( )
A.同旁内角互补,两直线平行
B.两直线平行,同旁内角互补
C.同位角互补,两直线平行
D.两直线平行,同位角互补
3.如图,已知直线a,b,c,d,且c⊥a,c⊥b,直线b,c,d交于一点.若∠1=48°,则∠2等于
°.
第3题图
第4题图
第5题图
4.如图,AB∥CD,CE∥GF.若∠1=60°,则∠2=
.
5.如图,直线l1∥l2,将一块含30°角的直角三角板按如图所示放置,若∠1=26°,则∠2=
°.
6.如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
(2)从∠1=110°可以知道∠3是多少度?为什么?
(3)从∠1=110°可以知道∠4是多少度?为什么?
7.如图,一条公路两次拐弯后,和原来的方向相同,第一次拐弯的角(∠B)是142°,第二次拐弯的角(∠C)是多少度?
8.填空,完成下列说理过程.
如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,试说明∠A+∠B+∠C=180°.
解:∵DE∥AC(已知),
∴∠1=∠
(
),
∠4=∠
(
).
∵AB∥EF(已知),
∴∠3=∠
(
),
∠2=∠
(
).
∴∠2=∠A(等量代换).
∵∠1+∠2+∠3=180°,∴∠A+∠B+∠C=180°(等量代换).
第
1
页
共
5
页
参考答案
自主学习
一、知识链接
解:有3种,(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行.
二、新知预习
1.两直线平行,同位角相等
2.两直线平行,内错角相等
3.两直线平行,同旁内角互补
练习:(1)=
两直线平行,同位角相等
(2)=
两直线平行,内错角相等
(3)180
两直线平行,同旁内角互补
合作探究
一、要点探究
探究点1:平行线的性质
猜想
:相等
例1
解:因为AB∥CD,所以∠1=∠3=50°.因为∠2+∠3=180°,所以∠2=130°.
例2
解:∵AB∥CD,∴∠EHD=∠EGB=50°.∴∠CHG=180°﹣∠EHD=180°﹣50°=130°.
∵HM平分∠CHG,∴∠CHM=∠GHM=∠CHG=65°.∵AB∥CD,∴∠GMH=∠CHM=65°.
【针对训练】1.C
2.C
3.120°
例3
解:如图,三角形A′B′C′即为所求.
探究点2:
例4
解:∵∠1=∠2,∴a∥b.∴∠5=∠3=30°.∴∠4=180°﹣∠5=150°.
例5
解:过点E作EF∥AB,则EF∥CD,如图所示.∵AB∥EF,∴∠BEF=180°﹣∠B=60°.
∵CD∥EF,∴∠DEF=180°﹣∠D=35°.∴∠BED=∠BEF+∠DEF=95°.
当堂检测
1.C
2.B
3.42
4.60°
5.34
6.解:(1)∵AB∥CD,∴∠2=∠1=110°(两直线平行,内错角相等).
(2)∵AB∥CD,∴∠1=∠3=110°(两直线平行,同位角相等).
(3)∵AB∥CD,∴∠4+∠1=180°(两直线平行,同旁内角互补).∴∠4=70°.
7.解:如图,∵一条公路两次拐弯后,和原来的方向相同,∴AB∥CD.
∵∠B=142°,∴∠C=∠B=142°.
答:第二次拐弯的角(∠C)是142°.
8.C
两直线平行,同位角相等
2
两直线平行,内错角相等
B
两直线平行,同位角相等
4
两直线平行,内错角相等
平行线的性质
学习目标:
1.掌握两直线平行,同位角、内错角相等,同旁内角互补,并能熟练运用(重点);
2.能够根据平行线的性质进行简单的推理(难点).
自主学习
一、知识链接
平行线的判定方法有哪几种?
二、新知预习
(预习课本P175-177)完成下列各题:
1.两条平行线被第三条直线所截,同位角相等,简单地说,就是
;
2.两条平行线被第三条直线所截,内错角相等,简单地说,就是
;
3.两条平行线被第三条直线所截,同旁内角互补,简单地说,就是
.
练习:如图,若AB平行CD,则有:
(1)∠3
∠5,理由是
;
(2)∠2
∠4,理由是
;
(3)∠1+∠4=
°,理由是
.
合作探究
要点探究
探究点1:平行线的性质
问题1:画两条平行线a,b,然后画一条截线c与a,b相交,标出如图所示的角.
度量所形成的8个角的度数,把结果填入下表:
角
∠1
∠2
∠3
∠4
度数
角
∠5
∠6
∠7
∠8
度数
观察:
∠1~
∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想.
猜想
:两条平行线被第三条直线所截,同位角
.
思考:再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?
【要点归纳】两条平行线被第三条直线所截,同位角相等.即两直线平行,同位角相等.
问题2:如图,已知a//b,那么∠2与∠3相等吗?为什么?
问题3:如图,已知a//b,那么∠2与∠4有什么关系呢?为什么?
【要点归纳】1.两条平行线被第三条直线所截,内错角相等.即:两直线平行,内错角相等.
2.两条平行线被第三条直线所截,同旁内角互补.即:两直线平行,同旁内角互补.
例1
如图,已知AB∥CD,∠1=50°,求∠2的度数.
例2
如图,AB∥CD,EF与AB,CD分别交于点G,H,∠CHG的平分线HM交AB于点M.若∠EGB=50°,求∠GMH的度数.
【针对训练】
1.如图,直线a∥b,∠1=70°,那么∠2的度数是(
)
A.50°
B.60°
C.70°
D.80°
第1题图
第2题图
第3题图
2.如图,直线l1,l2被直线l3所截,l1∥l2,与∠1相等的角是( )
A.∠2
B.∠3
C.∠4
D.∠5
3.如图,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为
.
例3
如图,三角形ABC的顶点都在方格纸的格点上,将三角形ABC向下平移3格,再向右平移4格.请在图中画出平移后的三角形A′B′C′.
探究点2:平行线的性质与判定的综合
例4
如图,∠1=∠2,∠3=30°,求∠4的度数.
例5
如图,AB∥CD,∠B=120°,∠D=145°,求∠BED的度数.
二、课堂小结
当堂检测
1.如图,直线a、b被直线c所截,a∥b,∠2=48°,则∠1的度数为( )
A.48°
B.58°
C.132°
D.122°
第1题图
第2题图
2.如图,已知a∥b,得到∠1+∠2=180°的依据( )
A.同旁内角互补,两直线平行
B.两直线平行,同旁内角互补
C.同位角互补,两直线平行
D.两直线平行,同位角互补
3.如图,已知直线a,b,c,d,且c⊥a,c⊥b,直线b,c,d交于一点.若∠1=48°,则∠2等于
°.
第3题图
第4题图
第5题图
4.如图,AB∥CD,CE∥GF.若∠1=60°,则∠2=
.
5.如图,直线l1∥l2,将一块含30°角的直角三角板按如图所示放置,若∠1=26°,则∠2=
°.
6.如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
(2)从∠1=110°可以知道∠3是多少度?为什么?
(3)从∠1=110°可以知道∠4是多少度?为什么?
7.如图,一条公路两次拐弯后,和原来的方向相同,第一次拐弯的角(∠B)是142°,第二次拐弯的角(∠C)是多少度?
8.填空,完成下列说理过程.
如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,试说明∠A+∠B+∠C=180°.
解:∵DE∥AC(已知),
∴∠1=∠
(
),
∠4=∠
(
).
∵AB∥EF(已知),
∴∠3=∠
(
),
∠2=∠
(
).
∴∠2=∠A(等量代换).
∵∠1+∠2+∠3=180°,∴∠A+∠B+∠C=180°(等量代换).
第
1
页
共
5
页
参考答案
自主学习
一、知识链接
解:有3种,(1)同位角相等,两直线平行;(2)内错角相等,两直线平行;(3)同旁内角互补,两直线平行.
二、新知预习
1.两直线平行,同位角相等
2.两直线平行,内错角相等
3.两直线平行,同旁内角互补
练习:(1)=
两直线平行,同位角相等
(2)=
两直线平行,内错角相等
(3)180
两直线平行,同旁内角互补
合作探究
一、要点探究
探究点1:平行线的性质
猜想
:相等
例1
解:因为AB∥CD,所以∠1=∠3=50°.因为∠2+∠3=180°,所以∠2=130°.
例2
解:∵AB∥CD,∴∠EHD=∠EGB=50°.∴∠CHG=180°﹣∠EHD=180°﹣50°=130°.
∵HM平分∠CHG,∴∠CHM=∠GHM=∠CHG=65°.∵AB∥CD,∴∠GMH=∠CHM=65°.
【针对训练】1.C
2.C
3.120°
例3
解:如图,三角形A′B′C′即为所求.
探究点2:
例4
解:∵∠1=∠2,∴a∥b.∴∠5=∠3=30°.∴∠4=180°﹣∠5=150°.
例5
解:过点E作EF∥AB,则EF∥CD,如图所示.∵AB∥EF,∴∠BEF=180°﹣∠B=60°.
∵CD∥EF,∴∠DEF=180°﹣∠D=35°.∴∠BED=∠BEF+∠DEF=95°.
当堂检测
1.C
2.B
3.42
4.60°
5.34
6.解:(1)∵AB∥CD,∴∠2=∠1=110°(两直线平行,内错角相等).
(2)∵AB∥CD,∴∠1=∠3=110°(两直线平行,同位角相等).
(3)∵AB∥CD,∴∠4+∠1=180°(两直线平行,同旁内角互补).∴∠4=70°.
7.解:如图,∵一条公路两次拐弯后,和原来的方向相同,∴AB∥CD.
∵∠B=142°,∴∠C=∠B=142°.
答:第二次拐弯的角(∠C)是142°.
8.C
两直线平行,同位角相等
2
两直线平行,内错角相等
B
两直线平行,同位角相等
4
两直线平行,内错角相等
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
