2020-2021学年北京课改新版八年级上册数学《第12章 三角形》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年北京课改新版八年级上册数学《第12章 三角形》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 242.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 21:44:32 | ||
图片预览



文档简介
2020-2021学年北京课改新版八年级上册数学《第12章
三角形》单元测试卷
一.选择题
1.图中三角形的个数是( )
A.3个
B.4个
C.5个
D.6个
2.已知△ABC的一个外角为50°,则△ABC一定是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.锐角三角形或钝角三角形
3.一天,爸爸带小明到建筑工地玩,看见一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于130°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是( )
A.50°
B.65°
C.90°
D.130°
4.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
5.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.两点确定一条直线
B.两点之间线段最短
C.三角形的稳定性
D.垂线段最短
6.如图,张叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是( )
A.三角形的稳定性
B.两点之间线段最短
C.垂线段最短
D.对顶角相等
7.以下列各组长度的线段为边,能构成三角形的是( )
A.4cm,8cm,12cm
B.5cm,6cm,14cm
C.10cm,10cm,8cm
D.3cm,9cm,5cm
8.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A.三边高的交点
B.三条角平分线的交点
C.三边垂直平分线的交点
D.三边中线的交点
9.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=∠CGE.
其中正确的结论的个数是( )
A.1
B.2
C.3
D.4
10.下列说法:①直线外一点到该直线的垂线段,是这个点到该直线的距离;②同旁内角互补;③过一点有且只有一条直线与已知直线平行;④三角形三条高至少有一条在三角形的内部;⑤垂直于同一条直线的两条直线平行;⑥三角形的角平分线是线段.其中说法正确的有( )
A.2个
B.3个
C.4个
D.5个
二.填空题
11.如图中的三角形的个数是
个.
12.电工师傅在安好电线杆后,为了防止电线杆倾倒,常常按图所示引两条拉线,这样做的数学道理是
.
13.如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=
.
14.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是
三角形.
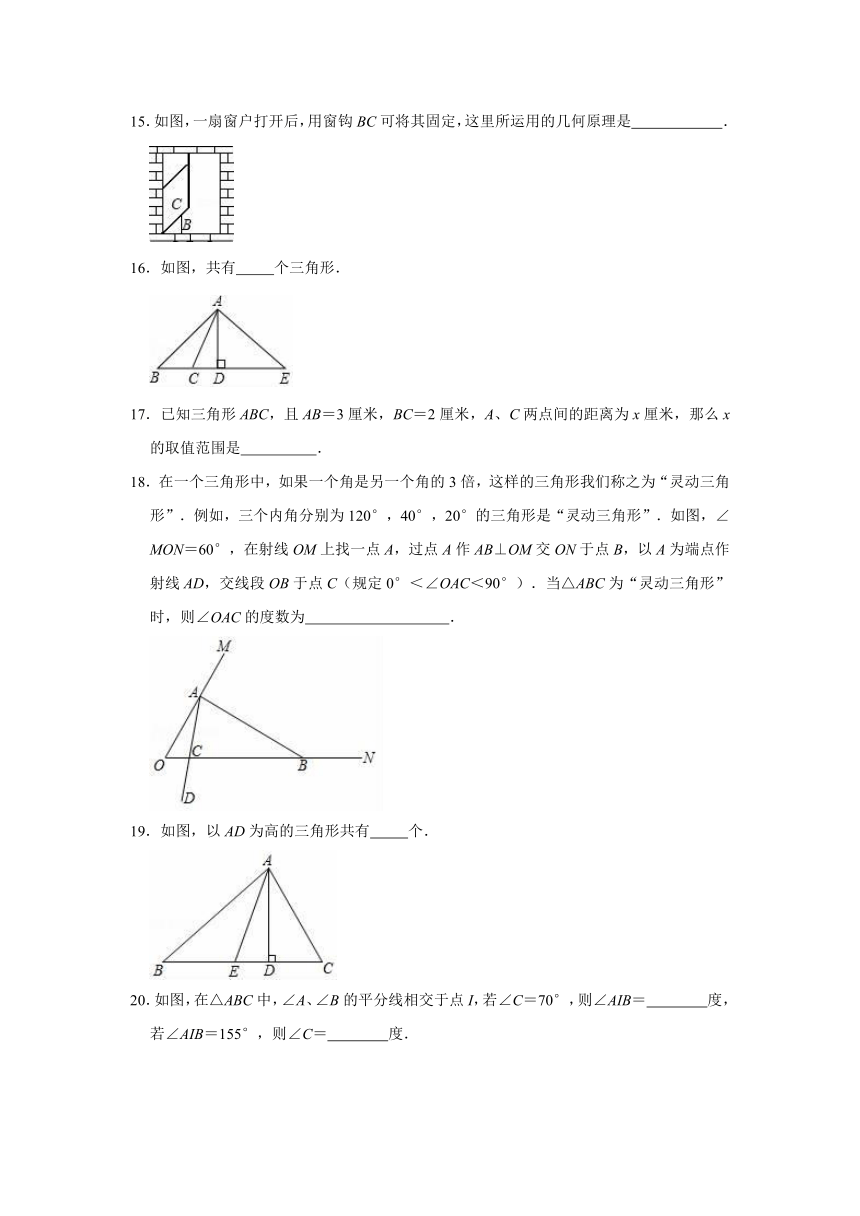
15.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是
.
16.如图,共有
个三角形.
17.已知三角形ABC,且AB=3厘米,BC=2厘米,A、C两点间的距离为x厘米,那么x的取值范围是
.
18.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).当△ABC为“灵动三角形”时,则∠OAC的度数为
.
19.如图,以AD为高的三角形共有
个.
20.如图,在△ABC中,∠A、∠B的平分线相交于点I,若∠C=70°,则∠AIB=
度,若∠AIB=155°,则∠C=
度.
三.解答题
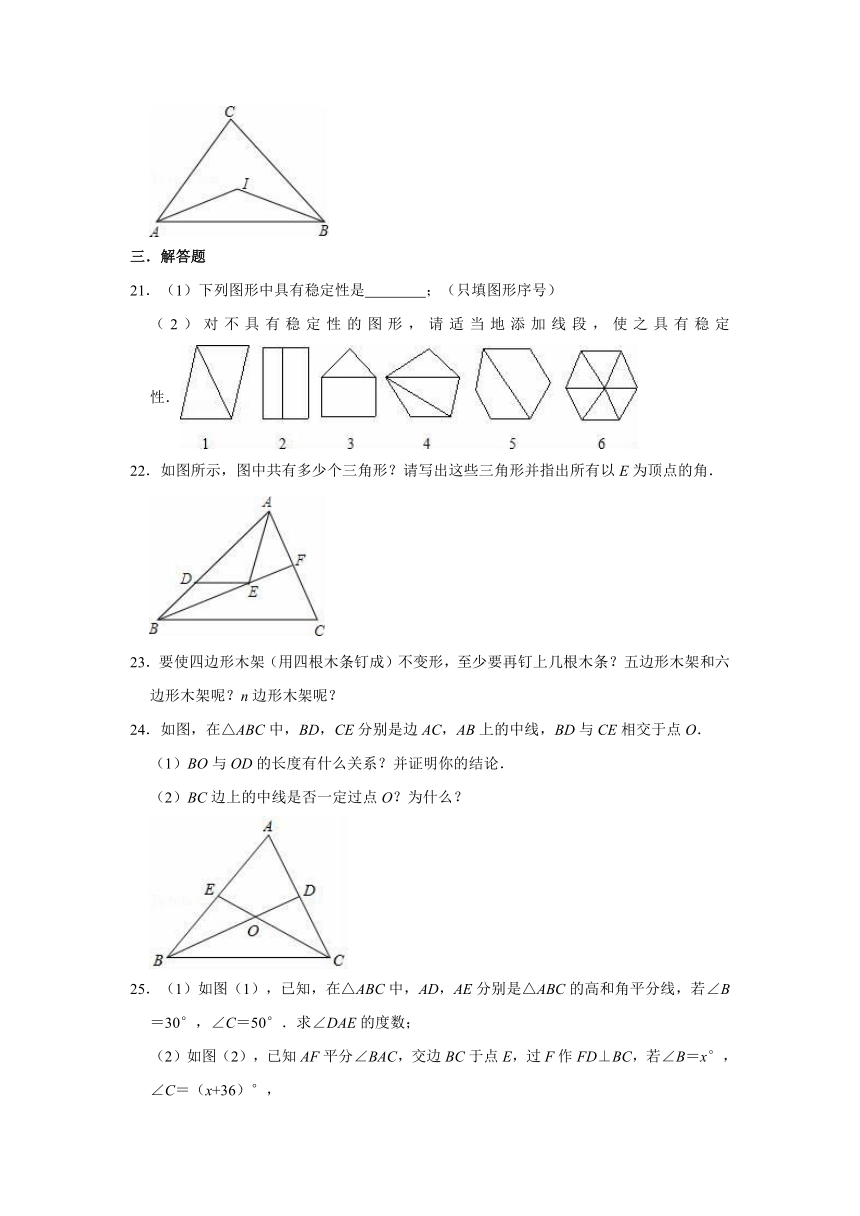
21.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
22.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
23.要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?
24.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O.
(1)BO与OD的长度有什么关系?并证明你的结论.
(2)BC边上的中线是否一定过点O?为什么?
25.(1)如图(1),已知,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),已知AF平分∠BAC,交边BC于点E,过F作FD⊥BC,若∠B=x°,∠C=(x+36)°,
①∠CAE=
(含x的代数式表示)
②求∠F的度数.
26.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有
个三角形.
27.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
①用含m的式子表示第三条边长;
②第一条边长能否为10米?为什么?
③若第一条边长最短,求m的取值范围.
参考答案与试题解析
一.选择题
1.解:BD,BE,BC,DE,DC,EC六条线段分别和A组成6个三角形.故选:D.
2.解:一个外角为50°,所以与它相邻的内角的度数为130°,所以三角形为钝角三角形.
故选:B.
3.解:根据题意,∠3﹣∠2=180°﹣∠1,
且∠1=130°,
即得∠3﹣∠2=50°.
故选:A.
4.解:三角形根据边分类,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
5.解:根据三角形的稳定性可固定窗户.
故选:C.
6.解:张叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是三角形的稳定性,
故选:A.
7.解:A、4+8=12,不能组成三角形,故此选项不合题意;
B、6+5<14,不能组成三角形,故此选项不符合题意;
C、10+8>10,能组成三角形,故此选项符合题意;
D、5+3=8<9,不能组成三角形,故此选项不合题意;
故选:C.
8.解:∵支撑点应是三角形的重心,
∴三角形的重心是三角形三边中线的交点,
故选:D.
9.解:∵EG∥BC,
∴∠CEG=∠ACB,
∵CD平分∠ACB,
∴∠ACB=2∠DCB,
∴∠CEG=2∠DCB,故①正确;
∵∠A=90°,
∴∠ACD+∠ADC=90°,
∵EG∥BC,且CG⊥EG于G,
∴∠CGE=∠GCB=90°,
∴∠GCD+∠BCD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC=∠GCD,故②正确;
无法证明CA平分∠BCG,故③错误;
∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+(∠ABC+∠ACB)=135°,
∴∠DFE=360°﹣135°﹣90°=135°,
∴∠DFB=45°=∠CGE,故④正确;
所以其中正确的结论为①②④共3个,
故选:C.
10.解:①直线外一点到该直线的垂线段的长度,是这个点到该直线的距离;故原命题错误;
②两直线平行,同旁内角互补;故原命题错误;
③过直线外一点有且只有一条直线与已知直线平行;故原命题错误;
④三角形三条高至少有一条在三角形的内部;故原命题正确;
⑤在同一平面内,垂直于同一条直线的两条直线平行;故原命题错误;
⑥三角形的角平分线是线段.故原命题正确;
其中说法正确的有2个,
故选:A.
二.填空题
11.解:5+4=9(个)
故答案为:9.
12.解:结合图形,为了防止电线杆倾倒,常常按图所示引两条拉线,两条拉线与地面就构成了三角形,所以这样做根据的数学道理是三角形的稳定性.
故答案是:三角形的稳定性.
13.解:∵点F是△ABC的重心,
∴EF=BF=×6=3,
∵AB=BC,BE是中线,
∴AE=AC=×8=4,BE⊥AC,
在Rt△AEF中,由勾股定理得,AF===5,
∴DF=AF=.
故答案为:.
14.解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
15.解:一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是三角形的稳定性.
故应填:三角形的稳定性.
16.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
17.解:∵△ABC中,AB=3厘米,BC=2厘米,A、C两点间的距离为x厘米,
∴3﹣2<x<3+2,
即:1<x<5,
故答案为:1<x<5.
18.解:设∠OAC=x则∠BAC=90°﹣x,∠ACB=60°+x,∠ABC=30°
∵△ABC为“灵动三角形”,
Ⅰ、当∠ABC=3∠BAC时,
∴30°=3(90°﹣x),
∴x=80°;
Ⅱ、当∠ABC=3∠ACB时,
∴30°=3(60°+x)∴x=﹣50°
(舍去)
∴此种情况不存在;
Ⅲ、当∠BCA=3∠BAC时,
∴60°+x=3(90°﹣x),
∴x=52.5°,
Ⅳ、当∠BCA=3∠ABC时,
∴60°+x=90°,
∴x=30°;
Ⅴ、当∠BAC=3∠ABC时,
∴90°﹣x=90°,
∴x=0°(舍去);
Ⅵ、当∠BAC=3∠ACB时,
∴90°﹣x=3(60°+x),
∴x=﹣22.5°(舍去),
∴此种情况不存在,
∴综上所述:∠OAC=80°或52.5°或30°.
故答案为:80°或52.5°或30°.
19.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6
20.解:连接CI并延长交AB于P.
∵AI平分∠CAP,
∴∠1=∠2.
∵BI平分∠CBP,
∴∠3=∠4,
∴∠1+∠3=(∠CAB+∠CBA)=×(180°﹣70°)=55°,
∴∠7+∠8=∠1+∠3+∠5+∠6=55°+70°=125°.
∵∠AIB=155°,
∴∠2+∠4=180°﹣155°=25°,
又∵∠CAP、∠CBP的平分线,相交于点I,
∴∠CAP+∠CBP=2×25°=50°,
∴∠ACB=180°﹣50°=130°.
三.解答题
21.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
22.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
23.解:四边形木架,至少要再钉上1根木条,使四边形变成两个三角形;
五边形木架,至少要再钉上2根木条,使五边形变成3个三角形;
六边形木架,至少要再钉上3根木条,使六边形变成4个三角形;
n边形木架,至少要再钉上(n﹣3)根木条,使多边形变成(n﹣2)个三角形.
24.解:(1)BO=2OD,理由如下:
连接DE,
∵BD、CE是边AC、AB上的中线,
∴DE∥BC,DE=BC.
∴△ODE∽△OBC,
∴=,
即BO=2OD.
(2)BC边上的中线一定过点O,
理由是:作BC边上的中线AF,交BD于M,
连接DF,
∵BD、AF是边AC、BC上的中线,
.∴DF∥BA,DF=BA.
∴△MDF∽△MBA
∴===,
即BD=3DM,
BO=BD,
∴O和M重合,
即BC边上的中线一定过点O.
25.解:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°﹣∠B﹣∠C=100°,
∵AE是∠BAC的平分线,
∴∠CAE=∠CAB=50°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=40°,
∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°;
(2)①∵∠B=x°,∠C=(x+36)°,AF平分∠BAC,
∴∠EAC=∠BAF,
∴∠CAE=
[180°﹣x°﹣(x+36)°]=72°﹣x°,
②∠AEC=∠BAE+∠B=72°,
∵FD⊥BC,
∴∠F=18°.
26.解:(1)
连接个数
1
2
3
4
5
6
出现三角形个数
3
6
10
15
21
28
(2)8个点;
(3)1+2+3+…+(n+1)
=
[1+2+3+…+(n+1)+1+2+3+…+(n+1)]
=(n+1)(n+2).
故答案为(n+1)(n+2).
27.解:(1)∵第二条边长为(3m﹣2)米,
∴第三条边长为50﹣m﹣(3m﹣2)=(52﹣4m)米;
(2)当m=10时,三边长分别为10,28,12,
由于10+12<28,所以不能构成三角形,即第一条边长不能为10米;
(3)由题意,得,
解得<m<9.
三角形》单元测试卷
一.选择题
1.图中三角形的个数是( )
A.3个
B.4个
C.5个
D.6个
2.已知△ABC的一个外角为50°,则△ABC一定是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.锐角三角形或钝角三角形
3.一天,爸爸带小明到建筑工地玩,看见一个如图所示的人字架,爸爸说:“小明,我考考你,这个人字架的夹角∠1等于130°,你知道∠3比∠2大多少吗?”小明马上得到了正确的答案,他的答案是( )
A.50°
B.65°
C.90°
D.130°
4.三角形按边分类可以用集合来表示,如图所示,图中小椭圆圈里的A表示( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.等边三角形
5.如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
A.两点确定一条直线
B.两点之间线段最短
C.三角形的稳定性
D.垂线段最短
6.如图,张叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是( )
A.三角形的稳定性
B.两点之间线段最短
C.垂线段最短
D.对顶角相等
7.以下列各组长度的线段为边,能构成三角形的是( )
A.4cm,8cm,12cm
B.5cm,6cm,14cm
C.10cm,10cm,8cm
D.3cm,9cm,5cm
8.如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A.三边高的交点
B.三条角平分线的交点
C.三边垂直平分线的交点
D.三边中线的交点
9.如图,△ABC的角平分线CD、BE相交于F,∠A=90°,EG∥BC,且CG⊥EG于G,下列结论:
①∠CEG=2∠DCB;②∠ADC=∠GCD;③CA平分∠BCG;④∠DFB=∠CGE.
其中正确的结论的个数是( )
A.1
B.2
C.3
D.4
10.下列说法:①直线外一点到该直线的垂线段,是这个点到该直线的距离;②同旁内角互补;③过一点有且只有一条直线与已知直线平行;④三角形三条高至少有一条在三角形的内部;⑤垂直于同一条直线的两条直线平行;⑥三角形的角平分线是线段.其中说法正确的有( )
A.2个
B.3个
C.4个
D.5个
二.填空题
11.如图中的三角形的个数是
个.
12.电工师傅在安好电线杆后,为了防止电线杆倾倒,常常按图所示引两条拉线,这样做的数学道理是
.
13.如图,△ABC中,AB=BC,AC=8,点F是△ABC的重心(即点F是△ABC的两条中线AD、BE的交点),BF=6,则DF=
.
14.一个三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,则这个三角形的形状是
三角形.
15.如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是
.
16.如图,共有
个三角形.
17.已知三角形ABC,且AB=3厘米,BC=2厘米,A、C两点间的距离为x厘米,那么x的取值范围是
.
18.在一个三角形中,如果一个角是另一个角的3倍,这样的三角形我们称之为“灵动三角形”.例如,三个内角分别为120°,40°,20°的三角形是“灵动三角形”.如图,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(规定0°<∠OAC<90°).当△ABC为“灵动三角形”时,则∠OAC的度数为
.
19.如图,以AD为高的三角形共有
个.
20.如图,在△ABC中,∠A、∠B的平分线相交于点I,若∠C=70°,则∠AIB=
度,若∠AIB=155°,则∠C=
度.
三.解答题
21.(1)下列图形中具有稳定性是
;(只填图形序号)
(2)对不具有稳定性的图形,请适当地添加线段,使之具有稳定性.
22.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
23.要使四边形木架(用四根木条钉成)不变形,至少要再钉上几根木条?五边形木架和六边形木架呢?n边形木架呢?
24.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O.
(1)BO与OD的长度有什么关系?并证明你的结论.
(2)BC边上的中线是否一定过点O?为什么?
25.(1)如图(1),已知,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.求∠DAE的度数;
(2)如图(2),已知AF平分∠BAC,交边BC于点E,过F作FD⊥BC,若∠B=x°,∠C=(x+36)°,
①∠CAE=
(含x的代数式表示)
②求∠F的度数.
26.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有
个三角形.
27.小刚准备用一段长50米的篱笆围成一个三角形形状的场地,用于饲养鸡,已知第一条边长为m米,由于条件限制第二条边长只能比第一条边长的3倍少2米.
①用含m的式子表示第三条边长;
②第一条边长能否为10米?为什么?
③若第一条边长最短,求m的取值范围.
参考答案与试题解析
一.选择题
1.解:BD,BE,BC,DE,DC,EC六条线段分别和A组成6个三角形.故选:D.
2.解:一个外角为50°,所以与它相邻的内角的度数为130°,所以三角形为钝角三角形.
故选:B.
3.解:根据题意,∠3﹣∠2=180°﹣∠1,
且∠1=130°,
即得∠3﹣∠2=50°.
故选:A.
4.解:三角形根据边分类,
∴图中小椭圆圈里的A表示等边三角形.
故选:D.
5.解:根据三角形的稳定性可固定窗户.
故选:C.
6.解:张叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是三角形的稳定性,
故选:A.
7.解:A、4+8=12,不能组成三角形,故此选项不合题意;
B、6+5<14,不能组成三角形,故此选项不符合题意;
C、10+8>10,能组成三角形,故此选项符合题意;
D、5+3=8<9,不能组成三角形,故此选项不合题意;
故选:C.
8.解:∵支撑点应是三角形的重心,
∴三角形的重心是三角形三边中线的交点,
故选:D.
9.解:∵EG∥BC,
∴∠CEG=∠ACB,
∵CD平分∠ACB,
∴∠ACB=2∠DCB,
∴∠CEG=2∠DCB,故①正确;
∵∠A=90°,
∴∠ACD+∠ADC=90°,
∵EG∥BC,且CG⊥EG于G,
∴∠CGE=∠GCB=90°,
∴∠GCD+∠BCD=90°,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ADC=∠GCD,故②正确;
无法证明CA平分∠BCG,故③错误;
∵∠EBC+∠ACB=∠AEB,∠DCB+∠ABC=∠ADC,
∴∠AEB+∠ADC=90°+(∠ABC+∠ACB)=135°,
∴∠DFE=360°﹣135°﹣90°=135°,
∴∠DFB=45°=∠CGE,故④正确;
所以其中正确的结论为①②④共3个,
故选:C.
10.解:①直线外一点到该直线的垂线段的长度,是这个点到该直线的距离;故原命题错误;
②两直线平行,同旁内角互补;故原命题错误;
③过直线外一点有且只有一条直线与已知直线平行;故原命题错误;
④三角形三条高至少有一条在三角形的内部;故原命题正确;
⑤在同一平面内,垂直于同一条直线的两条直线平行;故原命题错误;
⑥三角形的角平分线是线段.故原命题正确;
其中说法正确的有2个,
故选:A.
二.填空题
11.解:5+4=9(个)
故答案为:9.
12.解:结合图形,为了防止电线杆倾倒,常常按图所示引两条拉线,两条拉线与地面就构成了三角形,所以这样做根据的数学道理是三角形的稳定性.
故答案是:三角形的稳定性.
13.解:∵点F是△ABC的重心,
∴EF=BF=×6=3,
∵AB=BC,BE是中线,
∴AE=AC=×8=4,BE⊥AC,
在Rt△AEF中,由勾股定理得,AF===5,
∴DF=AF=.
故答案为:.
14.解:∵三角形两边上的高线交于一点,这个点正好是三角形的一个顶点,
∴这个三角形一定是直角三角形.
故答案为:直角.
15.解:一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是三角形的稳定性.
故应填:三角形的稳定性.
16.解:图中有:△ABC,△ABD,△ABE,△ACD,△ACE,△ADE,共6个.
故答案为:6
17.解:∵△ABC中,AB=3厘米,BC=2厘米,A、C两点间的距离为x厘米,
∴3﹣2<x<3+2,
即:1<x<5,
故答案为:1<x<5.
18.解:设∠OAC=x则∠BAC=90°﹣x,∠ACB=60°+x,∠ABC=30°
∵△ABC为“灵动三角形”,
Ⅰ、当∠ABC=3∠BAC时,
∴30°=3(90°﹣x),
∴x=80°;
Ⅱ、当∠ABC=3∠ACB时,
∴30°=3(60°+x)∴x=﹣50°
(舍去)
∴此种情况不存在;
Ⅲ、当∠BCA=3∠BAC时,
∴60°+x=3(90°﹣x),
∴x=52.5°,
Ⅳ、当∠BCA=3∠ABC时,
∴60°+x=90°,
∴x=30°;
Ⅴ、当∠BAC=3∠ABC时,
∴90°﹣x=90°,
∴x=0°(舍去);
Ⅵ、当∠BAC=3∠ACB时,
∴90°﹣x=3(60°+x),
∴x=﹣22.5°(舍去),
∴此种情况不存在,
∴综上所述:∠OAC=80°或52.5°或30°.
故答案为:80°或52.5°或30°.
19.解:∵AD⊥BC于D,
而图中有一边在直线CB上,且以A为顶点的三角形有6个,
∴以AD为高的三角形有6个.
故答案为:6
20.解:连接CI并延长交AB于P.
∵AI平分∠CAP,
∴∠1=∠2.
∵BI平分∠CBP,
∴∠3=∠4,
∴∠1+∠3=(∠CAB+∠CBA)=×(180°﹣70°)=55°,
∴∠7+∠8=∠1+∠3+∠5+∠6=55°+70°=125°.
∵∠AIB=155°,
∴∠2+∠4=180°﹣155°=25°,
又∵∠CAP、∠CBP的平分线,相交于点I,
∴∠CAP+∠CBP=2×25°=50°,
∴∠ACB=180°﹣50°=130°.
三.解答题
21.解:(1)具有稳定性的是①④⑥三个.
(2)如图所示:
22.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
23.解:四边形木架,至少要再钉上1根木条,使四边形变成两个三角形;
五边形木架,至少要再钉上2根木条,使五边形变成3个三角形;
六边形木架,至少要再钉上3根木条,使六边形变成4个三角形;
n边形木架,至少要再钉上(n﹣3)根木条,使多边形变成(n﹣2)个三角形.
24.解:(1)BO=2OD,理由如下:
连接DE,
∵BD、CE是边AC、AB上的中线,
∴DE∥BC,DE=BC.
∴△ODE∽△OBC,
∴=,
即BO=2OD.
(2)BC边上的中线一定过点O,
理由是:作BC边上的中线AF,交BD于M,
连接DF,
∵BD、AF是边AC、BC上的中线,
.∴DF∥BA,DF=BA.
∴△MDF∽△MBA
∴===,
即BD=3DM,
BO=BD,
∴O和M重合,
即BC边上的中线一定过点O.
25.解:(1)∵∠B=30°,∠C=50°,
∴∠CAB=180°﹣∠B﹣∠C=100°,
∵AE是∠BAC的平分线,
∴∠CAE=∠CAB=50°,
∵AD是△ABC的高,
∴∠ADC=90°,
∴∠CAD=90°﹣∠C=40°,
∴∠DAE=∠CAE﹣∠CAD=50°﹣40°=10°;
(2)①∵∠B=x°,∠C=(x+36)°,AF平分∠BAC,
∴∠EAC=∠BAF,
∴∠CAE=
[180°﹣x°﹣(x+36)°]=72°﹣x°,
②∠AEC=∠BAE+∠B=72°,
∵FD⊥BC,
∴∠F=18°.
26.解:(1)
连接个数
1
2
3
4
5
6
出现三角形个数
3
6
10
15
21
28
(2)8个点;
(3)1+2+3+…+(n+1)
=
[1+2+3+…+(n+1)+1+2+3+…+(n+1)]
=(n+1)(n+2).
故答案为(n+1)(n+2).
27.解:(1)∵第二条边长为(3m﹣2)米,
∴第三条边长为50﹣m﹣(3m﹣2)=(52﹣4m)米;
(2)当m=10时,三边长分别为10,28,12,
由于10+12<28,所以不能构成三角形,即第一条边长不能为10米;
(3)由题意,得,
解得<m<9.
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
