2020-2021学年北京课改新版七年级上册数学《第3章 简单的几何图形》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年北京课改新版七年级上册数学《第3章 简单的几何图形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 21:48:12 | ||
图片预览



文档简介
2020-2021学年北京课改新版七年级上册数学《第3章
简单的几何图形》单元测试卷
一.选择题
1.下列几何体,都是由平面围成的是( )
A.圆柱
B.三棱柱
C.圆锥
D.球
2.一个直棱柱有12个顶点,那么它的面的个数是( )
A.10个
B.9个
C.8个
D.7个
3.一个画家有14个边长为1m的正方体,他在地面上把它们摆成如下图的形状,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )
A.19m2
B.21m2
C.33m2
D.34m2
4.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
5.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
A.圆锥,正方体,三棱锥,圆柱
B.圆锥,正方体,四棱锥,圆柱
C.圆锥,正方体,四棱柱,圆柱
D.正方体,圆锥,圆柱,三棱柱
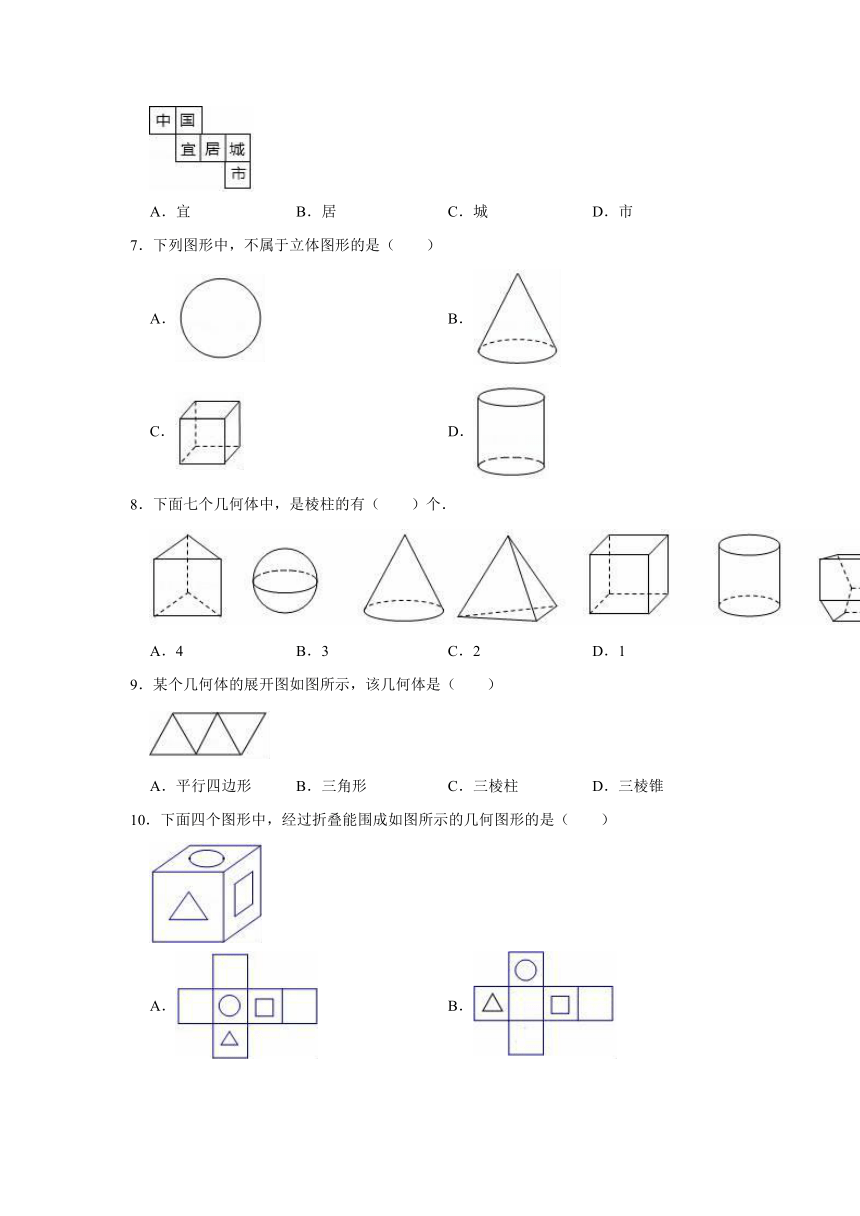
6.如图,正方体的平面展开图,每个面上都标有一个汉字,与“中”字相对的面上的字为( )
A.宜
B.居
C.城
D.市
7.下列图形中,不属于立体图形的是( )
A.
B.
C.
D.
8.下面七个几何体中,是棱柱的有( )个.
A.4
B.3
C.2
D.1
9.某个几何体的展开图如图所示,该几何体是( )
A.平行四边形
B.三角形
C.三棱柱
D.三棱锥
10.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
二.填空题
11.圆柱的表面展开图是
(用语言描述).
12.圆柱的侧面展开图是一个
,圆锥的侧面展开图是一个
,棱柱的侧面展开图是一个
.
13.一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为
.
14.如图所示,阴影部分的面积是大长方形面积的,是小长方形面积的,则大长方形空白的面积是小长方形空白的面积的
.
15.如图,在长方体ABCD﹣EFGH中,与平面BCGF平行的面是
.
16.把四个棱长为1cm的正方形按图示堆放于地面,则其表面积为
cm2.
17.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由
个面围成的,其中正方形有
个,长方形有
个.
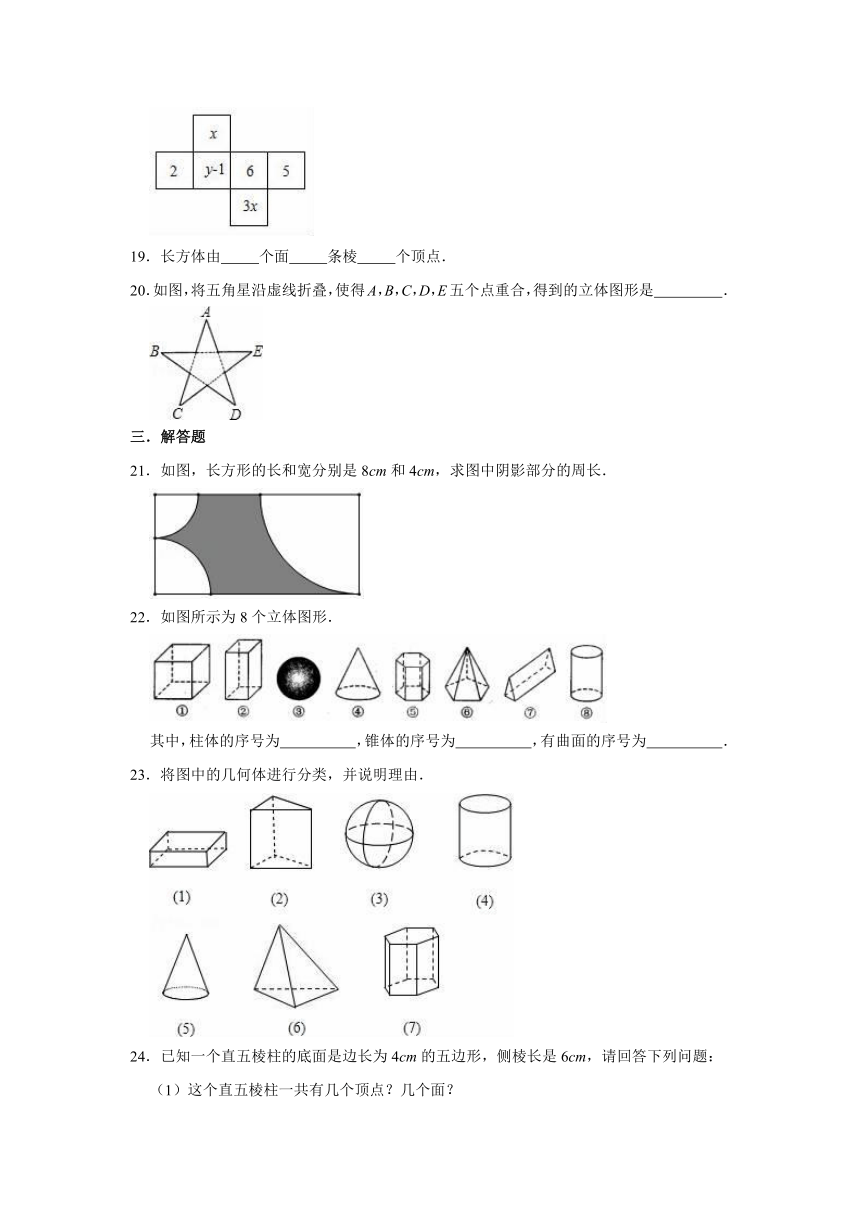
18.如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和都相等,则x﹣y=
.
19.长方体由
个面
条棱
个顶点.
20.如图,将五角星沿虚线折叠,使得A,B,C,D,E五个点重合,得到的立体图形是
.
三.解答题
21.如图,长方形的长和宽分别是8cm和4cm,求图中阴影部分的周长.
22.如图所示为8个立体图形.
其中,柱体的序号为
,锥体的序号为
,有曲面的序号为
.
23.将图中的几何体进行分类,并说明理由.
24.已知一个直五棱柱的底面是边长为4cm的五边形,侧棱长是6cm,请回答下列问题:
(1)这个直五棱柱一共有几个顶点?几个面?
(2)这个直五棱柱的侧面积是多少?
25.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
26.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
27.下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.
图号
顶点数x
棱数y
面数z
(a)
8
12
6
(b)
(c)
(d)
(e)
(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表;
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
参考答案与试题解析
一.选择题
1.解:圆柱的侧面是曲面,圆锥的侧面也是曲面,球是有曲面围成的,只有三棱柱是由5个平面围成的,
故选:B.
2.解:直棱柱有12个顶点,一定是六棱柱,
所以它有6个侧面和2个底面共8个面.
故选:C.
3.解:根据分析其表面积=4×(1+2+3)+9=33m2,即涂上颜色的为33m2.
故选:C.
4.解:A、球、圆锥是立体图形,错误;
B、棱锥、棱柱是立体图形,错误;
C、角、三角形、正方形、圆是平面图形,正确;
D、长方体是立体图形,错误;
故选:C.
5.解:根据几何体的平面展开图,则从左到右,其对应的几何体名称分别为:正方体,圆锥,圆柱,三棱柱.
故选:D.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“中”与“居”是相对面,
“国”与“市”是相对面,
“宜”与“城”是相对面.
故选:B.
7.解:圆是平面图形,不是立体图形,圆锥体、圆柱体、正方体都是立体图形,
故选:A.
8.解:如图,根据棱柱的特征可得,
①是三棱柱,②是球,③圆锥,④三棱锥,⑤正方体,⑥圆柱体,⑦六棱柱,
因此棱柱有:①⑤⑦,
故选:B.
9.解:观察图形可知,这个几何体是三棱锥.
故选:D.
10.解:由正方体图,得
三角形面、正方形面、圆面是邻面,故A符合题意,
故选:A.
二.填空题
11.解:圆柱的展开图是一个长方形和两个圆.
12.解:圆柱的侧面展开图是一个矩形,圆锥的侧面展开图是一个扇形,棱柱的侧面展开图是一个矩形.
13.解:根据等量关系列方程得:3×4×5=4πh,
故答案为:3×4×5=4πh.
14.解:设阴影部分的面积是a,
则大长方形面积是a=6a,小长方形面积是a=4a,
∴大长方形空白的面积是小长方形空白的面积的=,
故答案为:.
15.解:与平面BCGF平行的面是ADHE,
故答案为:ADHE.
16.解:从上面和下面看到的面积为2×3×(1×1),从正面和后面看面积为2×3×(1×1),从两个侧后面看面积为2×3×(1×1),故这个几何体的表面积为18cm2.
故答案为18cm2.
17.解:由图形可知,几何体的正面有2个长方形,和2个侧面,2个长方形的上面,1个正方形的底面,1个正方形的后面,总共有8个面;其中正方形有2个,长方形有4个.
故答案为:8,2,4.
18.解:根据正方体表面展开图的“相间、Z端是对面”可得,
“x”与“3x”的面是相对的,
“2”与“6”的面是相对的,
“y﹣1”与“5”的面是相对的,
又因为相对两面的数字之和都相等,
所以x+3x=2+6=y﹣1+5,
解得x=2,y=4,
所以x﹣y=2﹣4=﹣2,
故答案为:﹣2.
19.解:长方体属于四棱柱,四棱柱有6个面,12条棱,8个顶点.故答案为6,12,8.
20.解:底面是五边形,侧面是三角形,实际上是正五棱锥的展开图,所以是正五棱锥.
故答案为正五棱锥.
三.解答题
21.解:大弧长为:=2π(cm),
小弧长的和为:
2=π(cm),
周长为:2π+2π+2+6=(4π+8)cm,
答:图中阴影部分的周长为(4π+8)cm.
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:分类首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.
(1)长方体是由平面组成的,属于柱体.
(2)三棱柱是由平面组成的,属于柱体.
(3)球体是由曲面组成的,属于球体.
(4)圆柱是由平面和曲面组成的,属于柱体.
(5)圆锥是由曲面与平面组成的,属于锥体.
(6)四棱锥是由平面组成的,属于锥体.
(7)六棱柱是由平面组成的,属于柱体.
若按组成几何体的面的平或曲来划分:(1)(2)(6)(7)是一类,组成它的各面全是平面;(3)(4)(5)是一类,组成它的面至少有一个是曲面,
若按柱、锥、球来划分:(1)(2)(4)(7)是一类,即柱体;(5)(6)是一类,即锥体;(3)是球体.
24.解:(1)这个直五棱柱一共有10个顶点,7个面;
(2)4×6×5=120(cm2).
答:这个直五棱柱的侧面积是120cm2.
25.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
26.解:如图所示:
27.解:(1)见表:
图号
顶点数x
棱数y
面数z
(a)
8
12
6
(b)
6
9
5
(c)
8
12
6
(d)
8
13
7
(e)
10
15
7
(2)规律:x+z﹣2=y.
简单的几何图形》单元测试卷
一.选择题
1.下列几何体,都是由平面围成的是( )
A.圆柱
B.三棱柱
C.圆锥
D.球
2.一个直棱柱有12个顶点,那么它的面的个数是( )
A.10个
B.9个
C.8个
D.7个
3.一个画家有14个边长为1m的正方体,他在地面上把它们摆成如下图的形状,然后他把露出的表面都涂上颜色,那么被涂上颜色的总面积为( )
A.19m2
B.21m2
C.33m2
D.34m2
4.下列各组图形中都是平面图形的是( )
A.三角形、圆、球、圆锥
B.点、线段、棱锥、棱柱
C.角、三角形、正方形、圆
D.点、角、线段、长方体
5.如图所示为几何体的平面展开图,则从左到右,其对应的几何体名称分别为( )
A.圆锥,正方体,三棱锥,圆柱
B.圆锥,正方体,四棱锥,圆柱
C.圆锥,正方体,四棱柱,圆柱
D.正方体,圆锥,圆柱,三棱柱
6.如图,正方体的平面展开图,每个面上都标有一个汉字,与“中”字相对的面上的字为( )
A.宜
B.居
C.城
D.市
7.下列图形中,不属于立体图形的是( )
A.
B.
C.
D.
8.下面七个几何体中,是棱柱的有( )个.
A.4
B.3
C.2
D.1
9.某个几何体的展开图如图所示,该几何体是( )
A.平行四边形
B.三角形
C.三棱柱
D.三棱锥
10.下面四个图形中,经过折叠能围成如图所示的几何图形的是( )
A.
B.
C.
D.
二.填空题
11.圆柱的表面展开图是
(用语言描述).
12.圆柱的侧面展开图是一个
,圆锥的侧面展开图是一个
,棱柱的侧面展开图是一个
.
13.一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为
.
14.如图所示,阴影部分的面积是大长方形面积的,是小长方形面积的,则大长方形空白的面积是小长方形空白的面积的
.
15.如图,在长方体ABCD﹣EFGH中,与平面BCGF平行的面是
.
16.把四个棱长为1cm的正方形按图示堆放于地面,则其表面积为
cm2.
17.如图所示的几何体是由一个正方体截去后而形成的,这个几何体是由
个面围成的,其中正方形有
个,长方形有
个.
18.如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和都相等,则x﹣y=
.
19.长方体由
个面
条棱
个顶点.
20.如图,将五角星沿虚线折叠,使得A,B,C,D,E五个点重合,得到的立体图形是
.
三.解答题
21.如图,长方形的长和宽分别是8cm和4cm,求图中阴影部分的周长.
22.如图所示为8个立体图形.
其中,柱体的序号为
,锥体的序号为
,有曲面的序号为
.
23.将图中的几何体进行分类,并说明理由.
24.已知一个直五棱柱的底面是边长为4cm的五边形,侧棱长是6cm,请回答下列问题:
(1)这个直五棱柱一共有几个顶点?几个面?
(2)这个直五棱柱的侧面积是多少?
25.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
26.如图所示,在无阴影的方格中选出两个画出阴影,使它们与图中四个有阴影的正方形一起可以构成一正方体的表面展开图.(填出两种答案)
27.下列图形中,图(a)是正方体木块,把它切去一块,得到如图(b)(c)(d)(e)的木块.
图号
顶点数x
棱数y
面数z
(a)
8
12
6
(b)
(c)
(d)
(e)
(1)我们知道,图(a)的正方体木块有8个顶点、12条棱、6个面,请你将图(b)、(c)、(d)、(e)中木块的顶点数、棱数、面数填入下表;
(2)上表,各种木块的顶点数、棱数、面数之间的数量关系可以归纳出一定的规律,请你试写出顶点数x、棱数y、面数z之间的数量关系式.
参考答案与试题解析
一.选择题
1.解:圆柱的侧面是曲面,圆锥的侧面也是曲面,球是有曲面围成的,只有三棱柱是由5个平面围成的,
故选:B.
2.解:直棱柱有12个顶点,一定是六棱柱,
所以它有6个侧面和2个底面共8个面.
故选:C.
3.解:根据分析其表面积=4×(1+2+3)+9=33m2,即涂上颜色的为33m2.
故选:C.
4.解:A、球、圆锥是立体图形,错误;
B、棱锥、棱柱是立体图形,错误;
C、角、三角形、正方形、圆是平面图形,正确;
D、长方体是立体图形,错误;
故选:C.
5.解:根据几何体的平面展开图,则从左到右,其对应的几何体名称分别为:正方体,圆锥,圆柱,三棱柱.
故选:D.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“中”与“居”是相对面,
“国”与“市”是相对面,
“宜”与“城”是相对面.
故选:B.
7.解:圆是平面图形,不是立体图形,圆锥体、圆柱体、正方体都是立体图形,
故选:A.
8.解:如图,根据棱柱的特征可得,
①是三棱柱,②是球,③圆锥,④三棱锥,⑤正方体,⑥圆柱体,⑦六棱柱,
因此棱柱有:①⑤⑦,
故选:B.
9.解:观察图形可知,这个几何体是三棱锥.
故选:D.
10.解:由正方体图,得
三角形面、正方形面、圆面是邻面,故A符合题意,
故选:A.
二.填空题
11.解:圆柱的展开图是一个长方形和两个圆.
12.解:圆柱的侧面展开图是一个矩形,圆锥的侧面展开图是一个扇形,棱柱的侧面展开图是一个矩形.
13.解:根据等量关系列方程得:3×4×5=4πh,
故答案为:3×4×5=4πh.
14.解:设阴影部分的面积是a,
则大长方形面积是a=6a,小长方形面积是a=4a,
∴大长方形空白的面积是小长方形空白的面积的=,
故答案为:.
15.解:与平面BCGF平行的面是ADHE,
故答案为:ADHE.
16.解:从上面和下面看到的面积为2×3×(1×1),从正面和后面看面积为2×3×(1×1),从两个侧后面看面积为2×3×(1×1),故这个几何体的表面积为18cm2.
故答案为18cm2.
17.解:由图形可知,几何体的正面有2个长方形,和2个侧面,2个长方形的上面,1个正方形的底面,1个正方形的后面,总共有8个面;其中正方形有2个,长方形有4个.
故答案为:8,2,4.
18.解:根据正方体表面展开图的“相间、Z端是对面”可得,
“x”与“3x”的面是相对的,
“2”与“6”的面是相对的,
“y﹣1”与“5”的面是相对的,
又因为相对两面的数字之和都相等,
所以x+3x=2+6=y﹣1+5,
解得x=2,y=4,
所以x﹣y=2﹣4=﹣2,
故答案为:﹣2.
19.解:长方体属于四棱柱,四棱柱有6个面,12条棱,8个顶点.故答案为6,12,8.
20.解:底面是五边形,侧面是三角形,实际上是正五棱锥的展开图,所以是正五棱锥.
故答案为正五棱锥.
三.解答题
21.解:大弧长为:=2π(cm),
小弧长的和为:
2=π(cm),
周长为:2π+2π+2+6=(4π+8)cm,
答:图中阴影部分的周长为(4π+8)cm.
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:分类首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.
(1)长方体是由平面组成的,属于柱体.
(2)三棱柱是由平面组成的,属于柱体.
(3)球体是由曲面组成的,属于球体.
(4)圆柱是由平面和曲面组成的,属于柱体.
(5)圆锥是由曲面与平面组成的,属于锥体.
(6)四棱锥是由平面组成的,属于锥体.
(7)六棱柱是由平面组成的,属于柱体.
若按组成几何体的面的平或曲来划分:(1)(2)(6)(7)是一类,组成它的各面全是平面;(3)(4)(5)是一类,组成它的面至少有一个是曲面,
若按柱、锥、球来划分:(1)(2)(4)(7)是一类,即柱体;(5)(6)是一类,即锥体;(3)是球体.
24.解:(1)这个直五棱柱一共有10个顶点,7个面;
(2)4×6×5=120(cm2).
答:这个直五棱柱的侧面积是120cm2.
25.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
26.解:如图所示:
27.解:(1)见表:
图号
顶点数x
棱数y
面数z
(a)
8
12
6
(b)
6
9
5
(c)
8
12
6
(d)
8
13
7
(e)
10
15
7
(2)规律:x+z﹣2=y.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
