2020-2021学年鲁教五四新版八年级上册数学《第4章 图形的平移与旋转》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教五四新版八年级上册数学《第4章 图形的平移与旋转》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 280.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 21:49:24 | ||
图片预览


文档简介
2020-2021学年鲁教五四新版八年级上册数学《第4章
图形的平移与旋转》单元测试卷
一.选择题
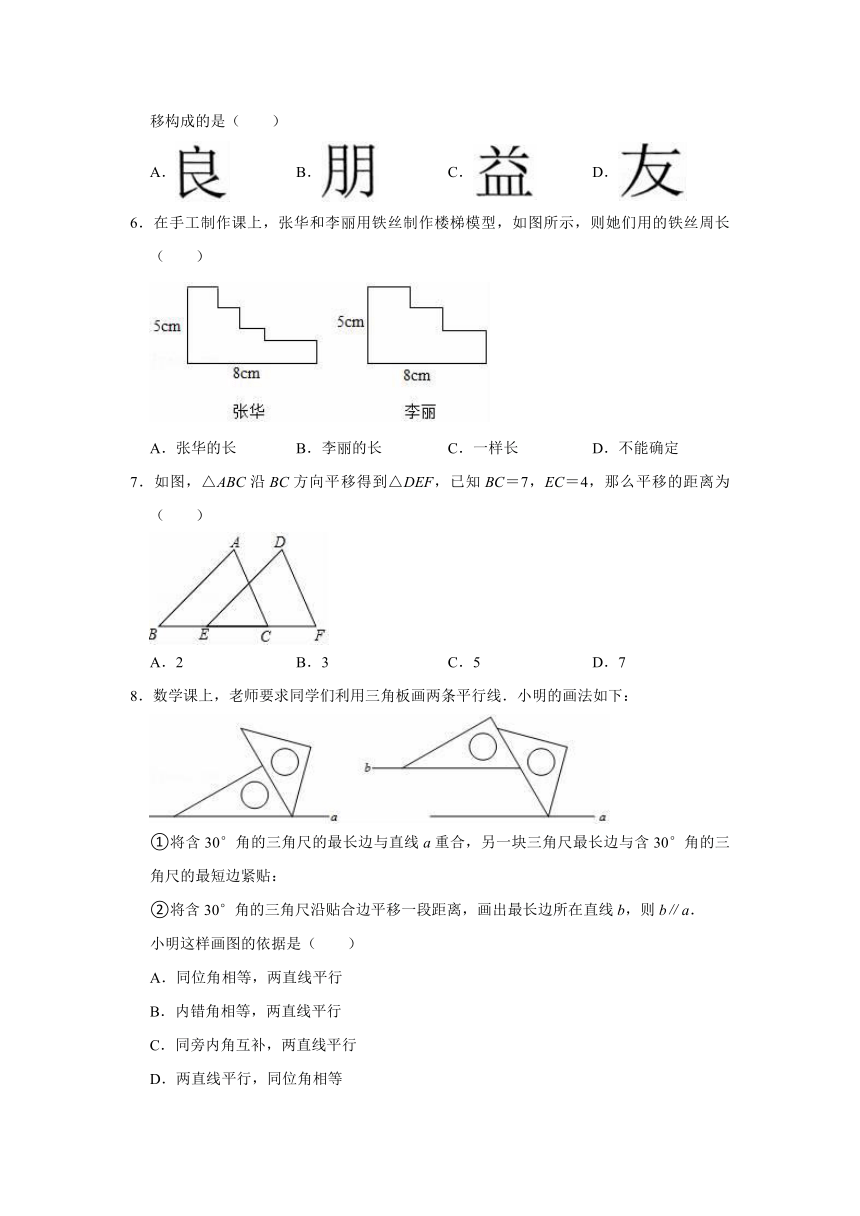
1.下列图形中,不能通过其中一个四边形平移得到的是( )
A.
B.
C.
D.
2.下列现象属于旋转的是( )
A.摩托车在急刹车是向前滑动
B.拧开自来水龙头
C.雪橇在雪地里滑动
D.空中下落的物体
3.如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( )
A.
B.
C.
D.
4.五角星可以看成由一个四边形旋转若干次而生成的,则每次旋转的度数可以是( )
A.36°
B.60°
C.72°
D.90°
5.现实世界中,平移现象无处不在,中国的方块字中有些也具有平移性,下列汉字是由平移构成的是( )
A.
B.
C.
D.
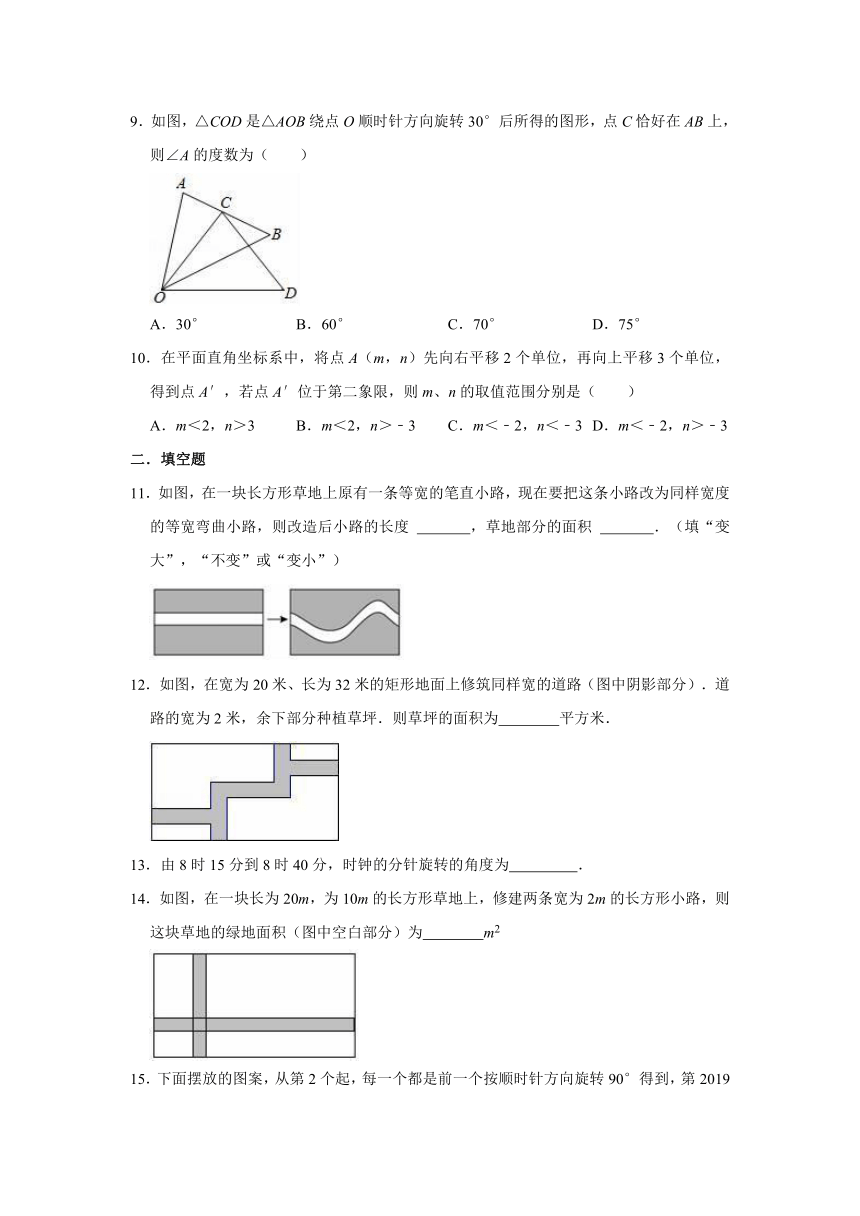
6.在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝周长( )
A.张华的长
B.李丽的长
C.一样长
D.不能确定
7.如图,△ABC沿BC方向平移得到△DEF,已知BC=7,EC=4,那么平移的距离为( )
A.2
B.3
C.5
D.7
8.数学课上,老师要求同学们利用三角板画两条平行线.小明的画法如下:
①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴:
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b∥a.
小明这样画图的依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
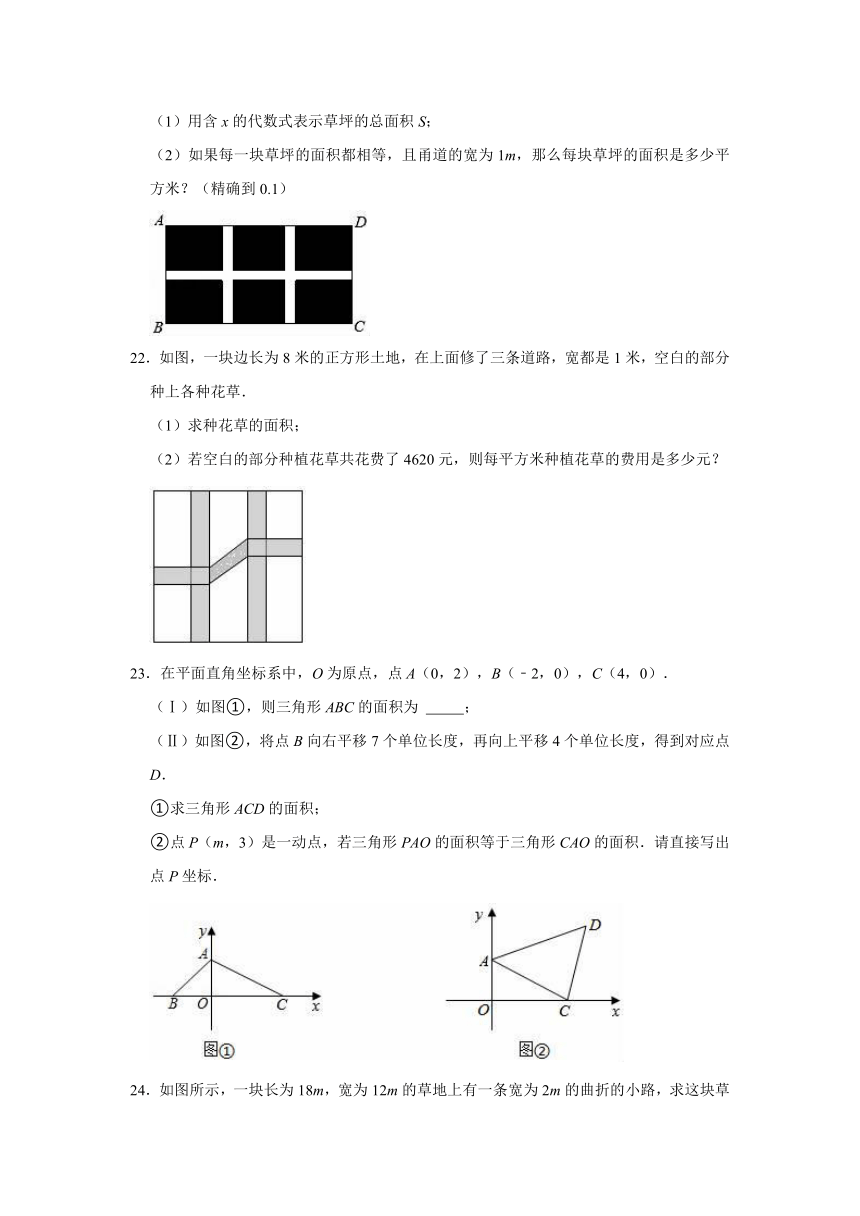
9.如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,则∠A的度数为( )
A.30°
B.60°
C.70°
D.75°
10.在平面直角坐标系中,将点A(m,n)先向右平移2个单位,再向上平移3个单位,得到点A′,若点A′位于第二象限,则m、n的取值范围分别是( )
A.m<2,n>3
B.m<2,n>﹣3
C.m<﹣2,n<﹣3
D.m<﹣2,n>﹣3
二.填空题
11.如图,在一块长方形草地上原有一条等宽的笔直小路,现在要把这条小路改为同样宽度的等宽弯曲小路,则改造后小路的长度
,草地部分的面积
.(填“变大”,“不变”或“变小”)
12.如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分).道路的宽为2米,余下部分种植草坪.则草坪的面积为
平方米.
13.由8时15分到8时40分,时钟的分针旋转的角度为
.
14.如图,在一块长为20m,为10m的长方形草地上,修建两条宽为2m的长方形小路,则这块草地的绿地面积(图中空白部分)为
m2
15.下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转90°得到,第2019个图案与第1个至第4个中的第
个箭头方向相同(填序号).
16.如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是
cm.
17.点(2,﹣1)向左平移3个单位长度得到的点在第
象限.
18.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移4cm得到△DEF.
已知AB=8cm,DH=3cm,则下列说法:
①CH∥DF;②∠DHA=∠F;③HE=5cm;④图中阴影部分面积为26cm2.
其中一定正确的是
.(把你认为正确结论的序号都填上)
19.将如图所示的图案绕其中心旋转n°时与原图案完全重合,那么n的最小值是
度.
20.已知,在Rt△ABC
中,∠C=90°,AC=9,BC=12,点D、E分别在边AC、BC上,且CD:CE=3:4.将△CDE绕点D顺时针旋转,当点C落在线段DE上的点F处时,BF恰好是∠ABC的平分线,此时线段CD的长是
.
三.解答题
21.小区规划一个长70m、宽30m的长方形草坪上修建三条同样宽的甬道,使其中两条与AB平行,另一条与BC平行,场地其余部分种草,甬道的宽度为xm.
(1)用含x的代数式表示草坪的总面积S;
(2)如果每一块草坪的面积都相等,且甬道的宽为1m,那么每块草坪的面积是多少平方米?(精确到0.1)
22.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)求种花草的面积;
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
23.在平面直角坐标系中,O为原点,点A(0,2),B(﹣2,0),C(4,0).
(Ⅰ)如图①,则三角形ABC的面积为
;
(Ⅱ)如图②,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形ACD的面积;
②点P(m,3)是一动点,若三角形PAO的面积等于三角形CAO的面积.请直接写出点P坐标.
24.如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,求这块草地的绿地面积.
25.如图所示,小方格边长为1单位,
(1)请写出△ABC各点的坐标:A
;B
;C
.
(2)求出S△ABC.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,在图中画出△A′B′C′.
26.(1)计算:
+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是
;在前16个图案中有
个;第2008个图案是
.
27.如图,已知AB∥CD,点E在直线AB,CD之间.
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿CD平移至FG.
①如图2,若∠AEC=90°,HF平分∠DFG,求∠AHF的度数;
②如图3,若HF平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
参考答案与试题解析
一.选择题
1.解:A、能通过其中一个四边形平移得到,故本选项不符合题意;
B、能通过其中一个四边形平移得到,故本选项不符合题意;
C、能通过其中一个四边形平移得到,故本选项不符合题意;
D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,故本选项符合题意.
故选:D.
2.解:A、C、D是平移,没有发生旋转,
B、拧开自来水龙头是旋转.
故选:B.
3.解:A、360°;
B、360°÷6=60°;
C、360°÷6=60°;
D、360°÷6=60°.
A的旋转角度与其它三个不同.
故选:A.
4.解:根据旋转的性质可知,每次旋转的度数可以是360°÷5=72°或72°的倍数.故选C.
5.解:根据题意,由两或三个完全相同的部分组成的汉字即可,
∴“朋”可以通过平移得到.
故选:B.
6.解:因为经过平移两个图形可变为两个长和宽都相等长方形,所以她们用的铁丝周长一样长.
故选:C.
7.解:由题意平移的距离为BE=BC﹣EC=7﹣4=3,
故选:B.
8.解:利用平移的性质得到∠1=∠2=60°,
所以a∥b.
故选:A.
9.解:∵△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,
∴AO=CO,∠AOC=30°,
∴∠A=∠ACO==75°,
故选:D.
10.解:将点A(m,n)先向右平移2个单位,再向上平移3个单位,得到点A′(m+2,n+3),
∵点A′位于第二象限,
∴,
解得:m<﹣2,n>﹣3,
故选:D.
二.填空题
11.解:改造后小路的长度变大,将第二个图的曲路两旁的部分通过平移整合为一个长方形,它的面积与第一个图形中两块草坪上下平移两块草坪得到的长方形的面积相等.
故答案为:变大;不变.
12.解:草坪的面积为:(32﹣2)×(20﹣2)=540(平方米).
故答案为:540.
13.解;由分针60分钟旋转360°,得
分针1分钟旋转360°÷60=6°,
分针旋转了40﹣15=25分钟,
8时15分到8时40分,时钟的分针旋转的角度为6°×25=150°,
故答案为:150°.
14.解:由图象可得,这块草地的绿地面积为:(20﹣2)×(10﹣2)=144(m2).
故答案为:144.
15.解:2019÷4=504…3,
故第2019个图案中的指针指向与第3个图案相同,
故答案为:3
16.解:根据题意,得A的对应点为A′,B的对应点为B′,C的对应点为C′,
所以BC=B′C′,BB′=CC′,
∴四边形AB′C′C的周长=CA+AB+BB′+B′C′+C′C=△ABC的周长+2BB′=20+4=24cm.
故答案为:24.
17.解:原来点的横坐标是2,纵坐标是﹣1,向左平移3个单位长度得到新点的横坐标是2﹣3=﹣1,纵坐标不变.
坐标为(﹣1,﹣1),点在第三象限.
故答案填:三.
18.解:∵Rt△ABC沿BC方向平移4cm得到Rt△DEF,
∴DE=AB=8cm,DE∥AB,AC∥DF,△ABC≌△DEF,BE=CF=4cm,
∴CH∥DF,所以①正确;
HE=DE﹣DH=8cm﹣3cm=5cm,所以③正确;
∵HE∥AB,
∴=,即=,解得CE=,
∴∠EHC>∠ECH,
∵HC∥DF,
∴∠F=∠ECH,
而∠EHC=∠DHA,
∴∠DHA>∠F,所以②错误;
∵S阴影部分=S△DEF﹣S△EHC=S△ABC﹣S△EHC=S梯形ABEH=×(5+8)×4=26(cm2),所以④正确.
故答案为①③④.
19.解:从六边形的中心及各顶点的图案来看,图案绕其中心最少旋转120°时能与原图案完全重合.
20.解:如图所示,设CD=3x,则CE=4x,BE=12﹣4x,
∵=,∠DCE=∠ACB=90°,
∴△ACB∽△DCE,
∴∠DEC=∠ABC,
∴AB∥DE,
∴∠ABF=∠BFE,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠EBF=∠EFB,
∴EF=BE=12﹣4x,
由旋转可得DF=CD=3x,
∵Rt△DCE中,CD2+CE2=DE2,
∴(3x)2+(4x)2=(3x+12﹣4x)2,
解得x1=2,x2=﹣3(舍去),
∴CD=2×3=6,
故答案为:6.
三.解答题
21.解:(1)S=70×30﹣(70x+2×30x﹣2x2)=2x2﹣130x+2100;
(2)当x=1时,S=2×12﹣130×1+2100=1972m2
所以每一块草坪的面积为1972÷6≈328.7m2
答:每一块草坪的面积约是328.7m2.
22.解:(1)(8﹣2)×(8﹣1)
=6×7
=42
(平方米)
答:种花草的面积为42平方米.
(2)4620÷42=110(元)
答:每平方米种植花草的费用是110元.
23.解:(Ⅰ)∵A(0,2),B(﹣2,0),C(4,0),
∴OA=2,OB=2,OC=4,
∴S△ABC=?BC?AO=×6×2=6.
故答案为6.
(Ⅱ)①如图②中由题意D(5,4),连接OD.
S△ACD=S△AOD+S△COD﹣S△AOC
=×2×5+×4×4﹣×2×4=9.
②由题意:×2×|m|=×2×4,
解得m=±4,
∴P(﹣4,3)或(4,3).
24.解:绿地的面积为:(18﹣2)×(12﹣2)=160(m2),
答:这块草地的绿地面积是160m2.
25.解:(1)观察图像可知:A(2,﹣1);
B(4,3);
C(1,2),
故答案为:(2,﹣1);(4,3);(1,2).
(2)S△ABC=××=5.
(3)如图,△A′B′C′即为所求作.
26.解:(1)原式==2;
(2)根据分析,知应分别为,5,.
27.解:(1)如图1,过点E作直线EN∥AB,
∵AB∥CD,
∴EN∥CD,
∴∠BAE=∠AEN,∠DCE=∠CEN,
∴∠AEC=∠AEN+∠CEN=∠BAH+∠ECD;
(2)∵AH平分∠BAE,
∴∠BAH=∠EAH,
①∵HF平分∠DFG,设∠GFH=∠DFH=x,
又CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠ECD,∠AEC=90°,
∴∠BAH=∠EAH=45°﹣x,
如图2,过点H作l∥AB,
易证∠AHF=∠BAH+∠DFH=45°﹣x+x=45°;
②设∠GFD=2x,∠BAH=∠EAH=y,
∵HF平分∠CFG,
∴∠GFH=∠CFH=90°﹣x,
由(1)知∠AEC=∠BAE+∠ECD=2x+2y,
如图3,过点H作l∥AB,
易证∠AHF﹣y+∠CFH=180°,
即∠AHF﹣y+90°﹣x=180°,∠AHF=90°+(x+y),
∴∠AHF=90°+∠AEC.(或2∠AHF﹣∠AEC=180°.)
图形的平移与旋转》单元测试卷
一.选择题
1.下列图形中,不能通过其中一个四边形平移得到的是( )
A.
B.
C.
D.
2.下列现象属于旋转的是( )
A.摩托车在急刹车是向前滑动
B.拧开自来水龙头
C.雪橇在雪地里滑动
D.空中下落的物体
3.如图,有四个图案,它们绕中心旋转一定的角度后,都能和原来的图案相互重合,其中有一个图案与其余三个图案旋转的角度不同,它是( )
A.
B.
C.
D.
4.五角星可以看成由一个四边形旋转若干次而生成的,则每次旋转的度数可以是( )
A.36°
B.60°
C.72°
D.90°
5.现实世界中,平移现象无处不在,中国的方块字中有些也具有平移性,下列汉字是由平移构成的是( )
A.
B.
C.
D.
6.在手工制作课上,张华和李丽用铁丝制作楼梯模型,如图所示,则她们用的铁丝周长( )
A.张华的长
B.李丽的长
C.一样长
D.不能确定
7.如图,△ABC沿BC方向平移得到△DEF,已知BC=7,EC=4,那么平移的距离为( )
A.2
B.3
C.5
D.7
8.数学课上,老师要求同学们利用三角板画两条平行线.小明的画法如下:
①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴:
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b∥a.
小明这样画图的依据是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
9.如图,△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,点C恰好在AB上,则∠A的度数为( )
A.30°
B.60°
C.70°
D.75°
10.在平面直角坐标系中,将点A(m,n)先向右平移2个单位,再向上平移3个单位,得到点A′,若点A′位于第二象限,则m、n的取值范围分别是( )
A.m<2,n>3
B.m<2,n>﹣3
C.m<﹣2,n<﹣3
D.m<﹣2,n>﹣3
二.填空题
11.如图,在一块长方形草地上原有一条等宽的笔直小路,现在要把这条小路改为同样宽度的等宽弯曲小路,则改造后小路的长度
,草地部分的面积
.(填“变大”,“不变”或“变小”)
12.如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分).道路的宽为2米,余下部分种植草坪.则草坪的面积为
平方米.
13.由8时15分到8时40分,时钟的分针旋转的角度为
.
14.如图,在一块长为20m,为10m的长方形草地上,修建两条宽为2m的长方形小路,则这块草地的绿地面积(图中空白部分)为
m2
15.下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转90°得到,第2019个图案与第1个至第4个中的第
个箭头方向相同(填序号).
16.如图,已知△ABC的周长为20cm,现将△ABC沿AB方向平移2cm至△A′B′C′的位置,连接CC′,则四边形AB′C′C的周长是
cm.
17.点(2,﹣1)向左平移3个单位长度得到的点在第
象限.
18.如图所示是重叠的两个直角三角形.将其中一个直角三角形沿BC方向平移4cm得到△DEF.
已知AB=8cm,DH=3cm,则下列说法:
①CH∥DF;②∠DHA=∠F;③HE=5cm;④图中阴影部分面积为26cm2.
其中一定正确的是
.(把你认为正确结论的序号都填上)
19.将如图所示的图案绕其中心旋转n°时与原图案完全重合,那么n的最小值是
度.
20.已知,在Rt△ABC
中,∠C=90°,AC=9,BC=12,点D、E分别在边AC、BC上,且CD:CE=3:4.将△CDE绕点D顺时针旋转,当点C落在线段DE上的点F处时,BF恰好是∠ABC的平分线,此时线段CD的长是
.
三.解答题
21.小区规划一个长70m、宽30m的长方形草坪上修建三条同样宽的甬道,使其中两条与AB平行,另一条与BC平行,场地其余部分种草,甬道的宽度为xm.
(1)用含x的代数式表示草坪的总面积S;
(2)如果每一块草坪的面积都相等,且甬道的宽为1m,那么每块草坪的面积是多少平方米?(精确到0.1)
22.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
(1)求种花草的面积;
(2)若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
23.在平面直角坐标系中,O为原点,点A(0,2),B(﹣2,0),C(4,0).
(Ⅰ)如图①,则三角形ABC的面积为
;
(Ⅱ)如图②,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.
①求三角形ACD的面积;
②点P(m,3)是一动点,若三角形PAO的面积等于三角形CAO的面积.请直接写出点P坐标.
24.如图所示,一块长为18m,宽为12m的草地上有一条宽为2m的曲折的小路,求这块草地的绿地面积.
25.如图所示,小方格边长为1单位,
(1)请写出△ABC各点的坐标:A
;B
;C
.
(2)求出S△ABC.
(3)若把△ABC向上平移2个单位,再向右平移2个单位得到△A′B′C′,在图中画出△A′B′C′.
26.(1)计算:
+﹣2﹣1;
(2)一串有趣的图案按一定规律排列.请仔细观察,按此规律画出的第10个图案是
;在前16个图案中有
个;第2008个图案是
.
27.如图,已知AB∥CD,点E在直线AB,CD之间.
(1)求证:∠AEC=∠BAE+∠ECD;
(2)若AH平分∠BAE,将线段CE沿CD平移至FG.
①如图2,若∠AEC=90°,HF平分∠DFG,求∠AHF的度数;
②如图3,若HF平分∠CFG,试判断∠AHF与∠AEC的数量关系并说明理由.
参考答案与试题解析
一.选择题
1.解:A、能通过其中一个四边形平移得到,故本选项不符合题意;
B、能通过其中一个四边形平移得到,故本选项不符合题意;
C、能通过其中一个四边形平移得到,故本选项不符合题意;
D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,故本选项符合题意.
故选:D.
2.解:A、C、D是平移,没有发生旋转,
B、拧开自来水龙头是旋转.
故选:B.
3.解:A、360°;
B、360°÷6=60°;
C、360°÷6=60°;
D、360°÷6=60°.
A的旋转角度与其它三个不同.
故选:A.
4.解:根据旋转的性质可知,每次旋转的度数可以是360°÷5=72°或72°的倍数.故选C.
5.解:根据题意,由两或三个完全相同的部分组成的汉字即可,
∴“朋”可以通过平移得到.
故选:B.
6.解:因为经过平移两个图形可变为两个长和宽都相等长方形,所以她们用的铁丝周长一样长.
故选:C.
7.解:由题意平移的距离为BE=BC﹣EC=7﹣4=3,
故选:B.
8.解:利用平移的性质得到∠1=∠2=60°,
所以a∥b.
故选:A.
9.解:∵△COD是△AOB绕点O顺时针方向旋转30°后所得的图形,
∴AO=CO,∠AOC=30°,
∴∠A=∠ACO==75°,
故选:D.
10.解:将点A(m,n)先向右平移2个单位,再向上平移3个单位,得到点A′(m+2,n+3),
∵点A′位于第二象限,
∴,
解得:m<﹣2,n>﹣3,
故选:D.
二.填空题
11.解:改造后小路的长度变大,将第二个图的曲路两旁的部分通过平移整合为一个长方形,它的面积与第一个图形中两块草坪上下平移两块草坪得到的长方形的面积相等.
故答案为:变大;不变.
12.解:草坪的面积为:(32﹣2)×(20﹣2)=540(平方米).
故答案为:540.
13.解;由分针60分钟旋转360°,得
分针1分钟旋转360°÷60=6°,
分针旋转了40﹣15=25分钟,
8时15分到8时40分,时钟的分针旋转的角度为6°×25=150°,
故答案为:150°.
14.解:由图象可得,这块草地的绿地面积为:(20﹣2)×(10﹣2)=144(m2).
故答案为:144.
15.解:2019÷4=504…3,
故第2019个图案中的指针指向与第3个图案相同,
故答案为:3
16.解:根据题意,得A的对应点为A′,B的对应点为B′,C的对应点为C′,
所以BC=B′C′,BB′=CC′,
∴四边形AB′C′C的周长=CA+AB+BB′+B′C′+C′C=△ABC的周长+2BB′=20+4=24cm.
故答案为:24.
17.解:原来点的横坐标是2,纵坐标是﹣1,向左平移3个单位长度得到新点的横坐标是2﹣3=﹣1,纵坐标不变.
坐标为(﹣1,﹣1),点在第三象限.
故答案填:三.
18.解:∵Rt△ABC沿BC方向平移4cm得到Rt△DEF,
∴DE=AB=8cm,DE∥AB,AC∥DF,△ABC≌△DEF,BE=CF=4cm,
∴CH∥DF,所以①正确;
HE=DE﹣DH=8cm﹣3cm=5cm,所以③正确;
∵HE∥AB,
∴=,即=,解得CE=,
∴∠EHC>∠ECH,
∵HC∥DF,
∴∠F=∠ECH,
而∠EHC=∠DHA,
∴∠DHA>∠F,所以②错误;
∵S阴影部分=S△DEF﹣S△EHC=S△ABC﹣S△EHC=S梯形ABEH=×(5+8)×4=26(cm2),所以④正确.
故答案为①③④.
19.解:从六边形的中心及各顶点的图案来看,图案绕其中心最少旋转120°时能与原图案完全重合.
20.解:如图所示,设CD=3x,则CE=4x,BE=12﹣4x,
∵=,∠DCE=∠ACB=90°,
∴△ACB∽△DCE,
∴∠DEC=∠ABC,
∴AB∥DE,
∴∠ABF=∠BFE,
又∵BF平分∠ABC,
∴∠ABF=∠CBF,
∴∠EBF=∠EFB,
∴EF=BE=12﹣4x,
由旋转可得DF=CD=3x,
∵Rt△DCE中,CD2+CE2=DE2,
∴(3x)2+(4x)2=(3x+12﹣4x)2,
解得x1=2,x2=﹣3(舍去),
∴CD=2×3=6,
故答案为:6.
三.解答题
21.解:(1)S=70×30﹣(70x+2×30x﹣2x2)=2x2﹣130x+2100;
(2)当x=1时,S=2×12﹣130×1+2100=1972m2
所以每一块草坪的面积为1972÷6≈328.7m2
答:每一块草坪的面积约是328.7m2.
22.解:(1)(8﹣2)×(8﹣1)
=6×7
=42
(平方米)
答:种花草的面积为42平方米.
(2)4620÷42=110(元)
答:每平方米种植花草的费用是110元.
23.解:(Ⅰ)∵A(0,2),B(﹣2,0),C(4,0),
∴OA=2,OB=2,OC=4,
∴S△ABC=?BC?AO=×6×2=6.
故答案为6.
(Ⅱ)①如图②中由题意D(5,4),连接OD.
S△ACD=S△AOD+S△COD﹣S△AOC
=×2×5+×4×4﹣×2×4=9.
②由题意:×2×|m|=×2×4,
解得m=±4,
∴P(﹣4,3)或(4,3).
24.解:绿地的面积为:(18﹣2)×(12﹣2)=160(m2),
答:这块草地的绿地面积是160m2.
25.解:(1)观察图像可知:A(2,﹣1);
B(4,3);
C(1,2),
故答案为:(2,﹣1);(4,3);(1,2).
(2)S△ABC=××=5.
(3)如图,△A′B′C′即为所求作.
26.解:(1)原式==2;
(2)根据分析,知应分别为,5,.
27.解:(1)如图1,过点E作直线EN∥AB,
∵AB∥CD,
∴EN∥CD,
∴∠BAE=∠AEN,∠DCE=∠CEN,
∴∠AEC=∠AEN+∠CEN=∠BAH+∠ECD;
(2)∵AH平分∠BAE,
∴∠BAH=∠EAH,
①∵HF平分∠DFG,设∠GFH=∠DFH=x,
又CE∥FG,
∴∠ECD=∠GFD=2x,
又∠AEC=∠BAE+∠ECD,∠AEC=90°,
∴∠BAH=∠EAH=45°﹣x,
如图2,过点H作l∥AB,
易证∠AHF=∠BAH+∠DFH=45°﹣x+x=45°;
②设∠GFD=2x,∠BAH=∠EAH=y,
∵HF平分∠CFG,
∴∠GFH=∠CFH=90°﹣x,
由(1)知∠AEC=∠BAE+∠ECD=2x+2y,
如图3,过点H作l∥AB,
易证∠AHF﹣y+∠CFH=180°,
即∠AHF﹣y+90°﹣x=180°,∠AHF=90°+(x+y),
∴∠AHF=90°+∠AEC.(或2∠AHF﹣∠AEC=180°.)
