2020-2021学年鲁教五四新版九年级上册数学《第4章 投影与视图》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教五四新版九年级上册数学《第4章 投影与视图》单元测试卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 282.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 21:52:27 | ||
图片预览

文档简介
2020-2021学年鲁教五四新版九年级上册数学《第4章
投影与视图》单元测试卷
一.选择题
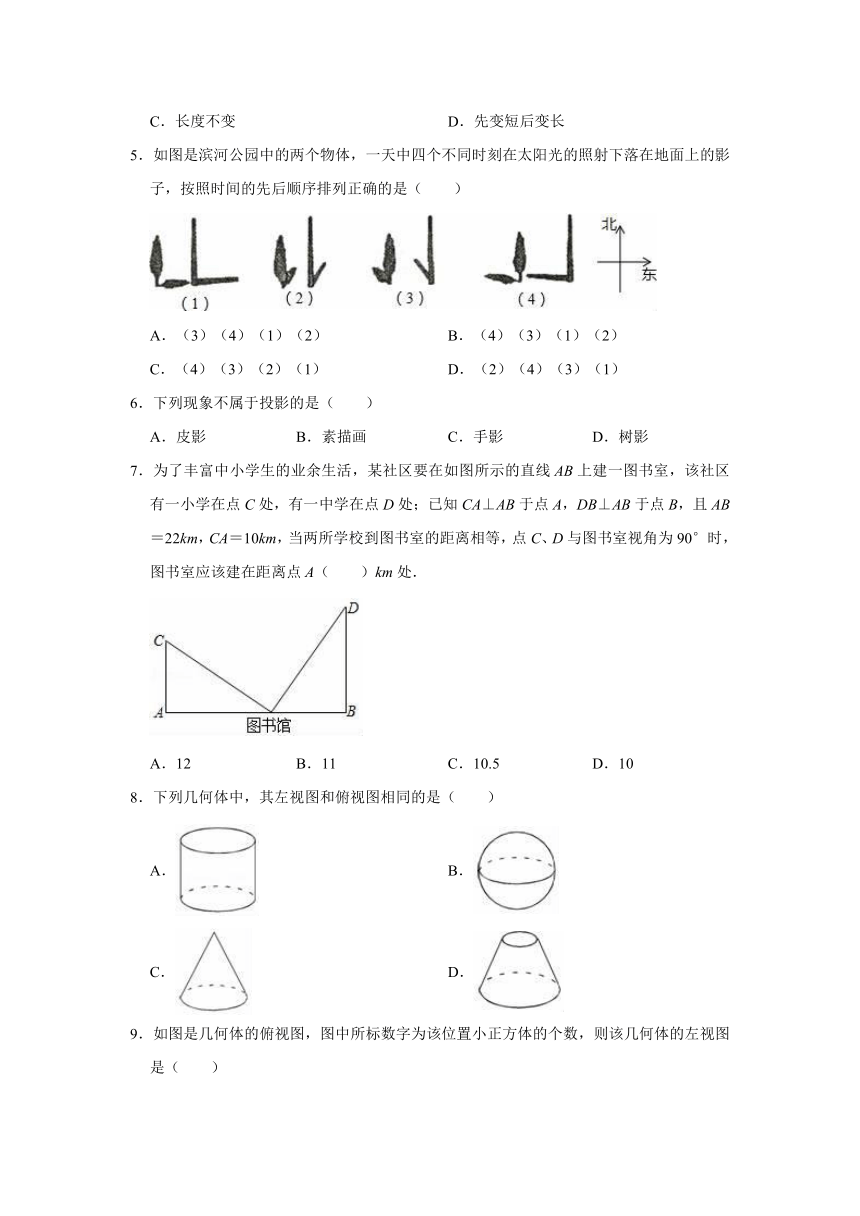
1.如图,下列水平放置的几何体中,左视图不是矩形的是( )
A.
B.
C.
D.
2.如图物体的左视图是( )
A.
B.
C.
D.
3.如图所示的几何体从上面看到的形状图是( )
A.
B.
C.
D.
4.如图,小明夜晚从路灯下A处走到B处这一过程中,他在路上的影子( )
A.逐渐变长
B.逐渐变短
C.长度不变
D.先变短后变长
5.如图是滨河公园中的两个物体,一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序排列正确的是( )
A.(3)(4)(1)(2)
B.(4)(3)(1)(2)
C.(4)(3)(2)(1)
D.(2)(4)(3)(1)
6.下列现象不属于投影的是( )
A.皮影
B.素描画
C.手影
D.树影
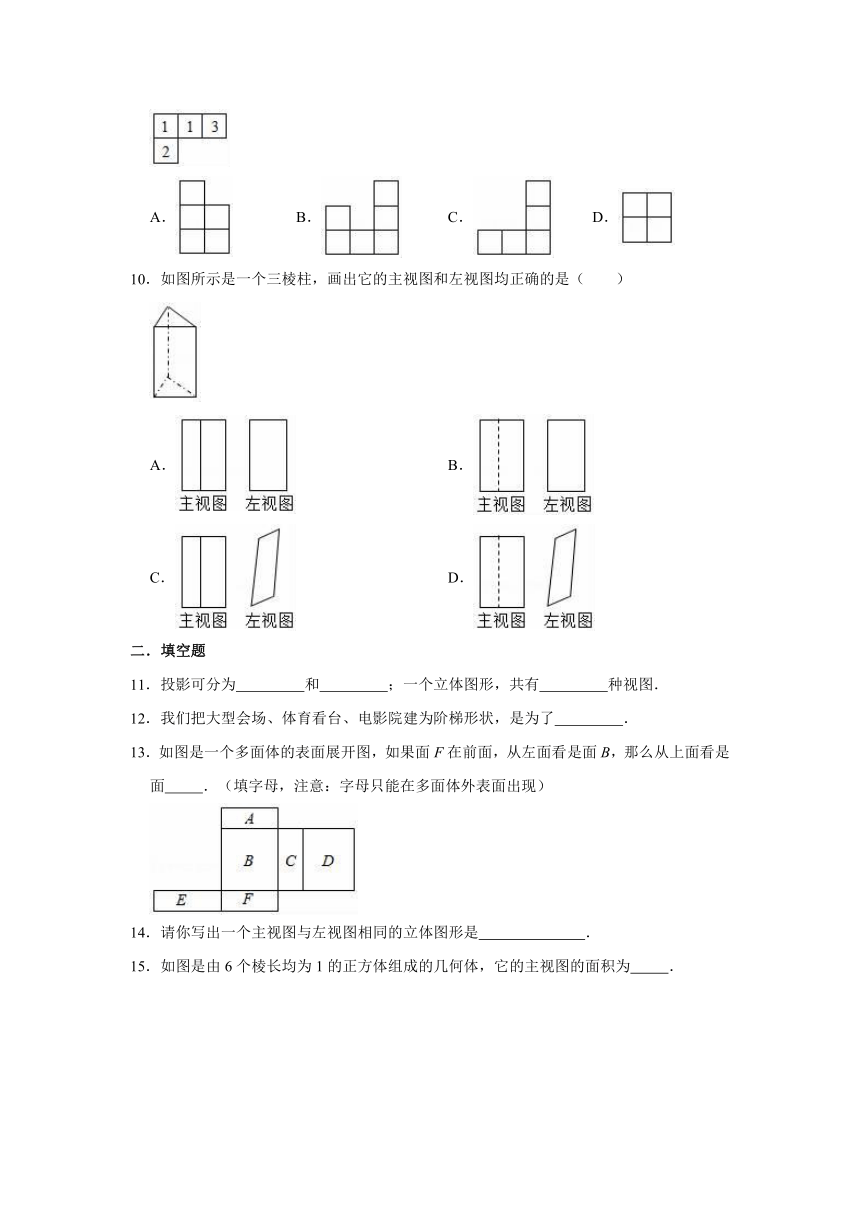
7.为了丰富中小学生的业余生活,某社区要在如图所示的直线AB上建一图书室,该社区有一小学在点C处,有一中学在点D处;已知CA⊥AB于点A,DB⊥AB于点B,且AB=22km,CA=10km,当两所学校到图书室的距离相等,点C、D与图书室视角为90°时,图书室应该建在距离点A( )km处.
A.12
B.11
C.10.5
D.10
8.下列几何体中,其左视图和俯视图相同的是( )
A.
B.
C.
D.
9.如图是几何体的俯视图,图中所标数字为该位置小正方体的个数,则该几何体的左视图是( )
A.
B.
C.
D.
10.如图所示是一个三棱柱,画出它的主视图和左视图均正确的是( )
A.
B.
C.
D.
二.填空题
11.投影可分为
和
;一个立体图形,共有
种视图.
12.我们把大型会场、体育看台、电影院建为阶梯形状,是为了
.
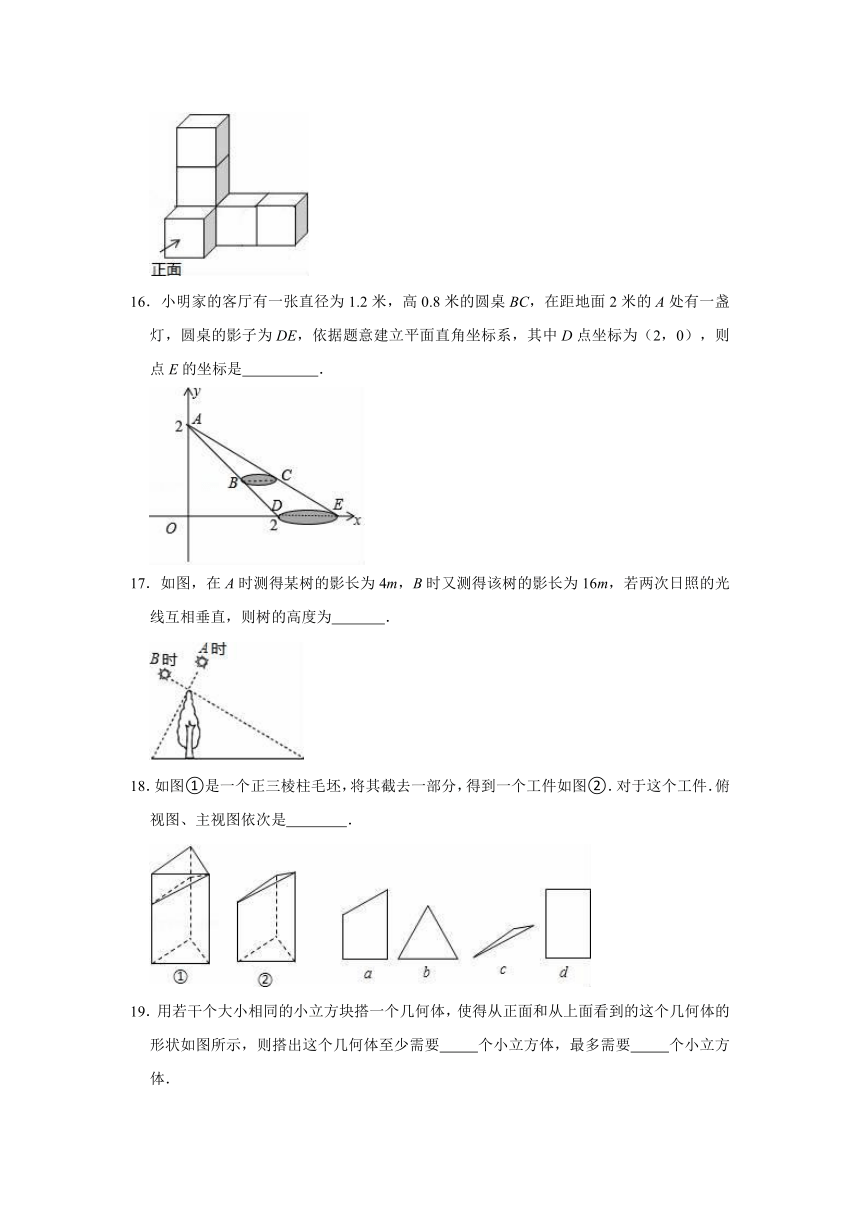
13.如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面
.(填字母,注意:字母只能在多面体外表面出现)
14.请你写出一个主视图与左视图相同的立体图形是
.
15.如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为
.
16.小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是
.
17.如图,在A时测得某树的影长为4m,B时又测得该树的影长为16m,若两次日照的光线互相垂直,则树的高度为
.
18.如图①是一个正三棱柱毛坯,将其截去一部分,得到一个工件如图②.对于这个工件.俯视图、主视图依次是
.
19.用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示,则搭出这个几何体至少需要
个小立方体,最多需要
个小立方体.
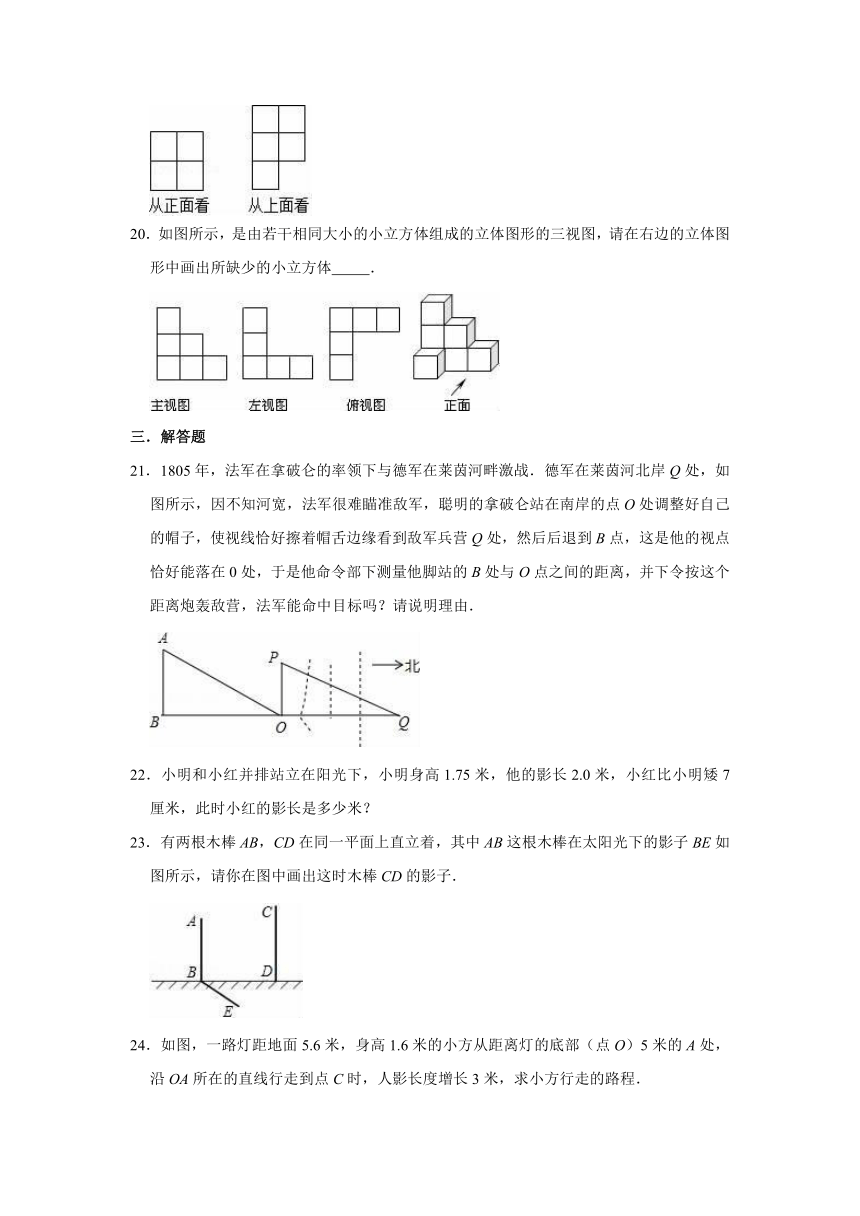
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体
.
三.解答题
21.1805年,法军在拿破仑的率领下与德军在莱茵河畔激战.德军在莱茵河北岸Q处,如图所示,因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸的点O处调整好自己的帽子,使视线恰好擦着帽舌边缘看到敌军兵营Q处,然后后退到B点,这是他的视点恰好能落在0处,于是他命令部下测量他脚站的B处与O点之间的距离,并下令按这个距离炮轰敌营,法军能命中目标吗?请说明理由.
22.小明和小红并排站立在阳光下,小明身高1.75米,他的影长2.0米,小红比小明矮7厘米,此时小红的影长是多少米?
23.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
24.如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
25.如图是由8个相同的小立方体组成的几何体,请在下列方框内画出它的三视图.
26.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V=
cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm
1
2
3
4
5
V/cm3
160
216
80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
参考答案与试题解析
一.选择题
1.解:A、圆柱的左视图是矩形,故本选项错误;
B、圆锥的左视图是等腰三角形,故本选项正确;
C、三棱柱的左视图是矩形,故本选项错误;
D、长方体的左视图是矩形,故本选项错误.
故选:B.
2.解:从左边看,是一列两个小正方形.
故选:D.
3.解:从上面看共有两层,底层右边是1个小正方形,上层有2个小正方形.
故选:D.
4.解:当他远离路灯走向B处时,光线与地面的夹角越来越小,小明在地面上留下的影子越来越长,
所以他在走过一盏路灯的过程中,其影子的长度逐渐变长,
故选:A.
5.解:按照时间的先后顺序排列正确的是(4)、(3)、(2)、(1).
故选:C.
6.解:根据平行投影的概念可知,素描画不是光线照射形成的.
故选:B.
7.解:设图书馆为点E,由题意得,EC=ED,EC⊥ED,
∵∠AEC+∠DEB=180°﹣90°,∠DEB+∠D=90°,
∴∠AEC=∠D,∠A=∠B=90°,
在Rt△AEC和Rt△BDE中,
,
∴△AEC≌△BDE(AAS),
∴AC=BE=10,
∴AE=AB﹣BE=22﹣10=12,
故选:A.
8.解:A、圆柱的左视图和俯视图分别为长方形,圆,故A选项不符合题意;
B、球的左视图和俯视图都是圆,故B选项符合题意;
C、圆锥的左视图和俯视图分别为等腰三角形,圆及圆心,故C选项不符合题意;
D、圆台的左视图和俯视图分别为梯形,圆环,故D选项不符合题意.
故选:B.
9.解:该几何体的左视图如图所示:.
故选:A.
10.解:如图所示的一个三棱柱,它的主视图和左视图是.
故选:B.
二.填空题
11.解:投影可分为平行投影和中心投影;一个立体图形,共有三种视图,
故答案为:平行投影,中心投影,三.
12.解:把大型会场、体育看台、电影院建为阶梯形状,是为了使后面的观众有更大的视野,从而减小盲区.
13.解:由题意可知,该图形是一个长方体的表面展开图,A面对应F面,B面对应D面,C面对应E面,
∵面F在前面,
∴面A在后面,
∵面B在左面,
∴面D在右面,
∴E在下面,C在上面.
故答案为:C.
14.解:球体的主视图与左视图都为圆.
故答案为:圆球(答案不唯一).
15.解:主视图如图所示,
∵由6个棱长均为1的正方体组成的几何体,
∴主视图的面积为5×12=5,
故答案为5.
16.解:∵BC∥DE,
∴△ABC∽△ADE,
∴,
∵BC=1.2,
∴DE=2,
∴E(4,0).
故答案为:(4,0).
17.解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED?FD,
代入数据可得DC2=64,
DC=8;
故答案为:8m.
18.解:从上面看可得到一个等边三角形,从正面看可得到一个直角梯形,所以俯视图、主视图依次是b、a.
故答案为:b、a.
19.解:∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体;最多有5个正方体,
∴该组合几何体最少有5+2=7个正方体,最多有5+5=10个正方体.
故答案为:7,10.
20.解:
三.解答题
21.解:根据题意知AB=PO,∠A=∠P,
又∵AB⊥BO,PO⊥BQ,
∴∠ABO=∠POQ=90°,
在△ABO和△POQ中,
,
∴△ABO≌△POQ(ASA),
∴BO=OQ,
故按这个距离炮轰敌营,法军能命中目标.
22.解:设小红的影长是x米,
根据题意得=,
解得x=1.92.
答:小红的影长是1.92米.
23.解:
24.解:∵AE⊥OD,GO⊥OD,
∴EA∥GO,
∴△AEB∽△OGB,
∴=,
∴=,
解得AB=2(m);
∵OA所在的直线行走到点C时,人影长度增长3米,
∴DC=5(m),
同理可得△DFC∽△DGO,
∴=,
即=,
解得AC=7.5(m).
答:小方行走的路程AC为7.5m.
25.解:
26.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x)?(12﹣2x)?x,
故答案为:(18﹣2x)?(12﹣2x)?x,
(2)把x=2代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=14×8×2=224,
把x=4代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
投影与视图》单元测试卷
一.选择题
1.如图,下列水平放置的几何体中,左视图不是矩形的是( )
A.
B.
C.
D.
2.如图物体的左视图是( )
A.
B.
C.
D.
3.如图所示的几何体从上面看到的形状图是( )
A.
B.
C.
D.
4.如图,小明夜晚从路灯下A处走到B处这一过程中,他在路上的影子( )
A.逐渐变长
B.逐渐变短
C.长度不变
D.先变短后变长
5.如图是滨河公园中的两个物体,一天中四个不同时刻在太阳光的照射下落在地面上的影子,按照时间的先后顺序排列正确的是( )
A.(3)(4)(1)(2)
B.(4)(3)(1)(2)
C.(4)(3)(2)(1)
D.(2)(4)(3)(1)
6.下列现象不属于投影的是( )
A.皮影
B.素描画
C.手影
D.树影
7.为了丰富中小学生的业余生活,某社区要在如图所示的直线AB上建一图书室,该社区有一小学在点C处,有一中学在点D处;已知CA⊥AB于点A,DB⊥AB于点B,且AB=22km,CA=10km,当两所学校到图书室的距离相等,点C、D与图书室视角为90°时,图书室应该建在距离点A( )km处.
A.12
B.11
C.10.5
D.10
8.下列几何体中,其左视图和俯视图相同的是( )
A.
B.
C.
D.
9.如图是几何体的俯视图,图中所标数字为该位置小正方体的个数,则该几何体的左视图是( )
A.
B.
C.
D.
10.如图所示是一个三棱柱,画出它的主视图和左视图均正确的是( )
A.
B.
C.
D.
二.填空题
11.投影可分为
和
;一个立体图形,共有
种视图.
12.我们把大型会场、体育看台、电影院建为阶梯形状,是为了
.
13.如图是一个多面体的表面展开图,如果面F在前面,从左面看是面B,那么从上面看是面
.(填字母,注意:字母只能在多面体外表面出现)
14.请你写出一个主视图与左视图相同的立体图形是
.
15.如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为
.
16.小明家的客厅有一张直径为1.2米,高0.8米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中D点坐标为(2,0),则点E的坐标是
.
17.如图,在A时测得某树的影长为4m,B时又测得该树的影长为16m,若两次日照的光线互相垂直,则树的高度为
.
18.如图①是一个正三棱柱毛坯,将其截去一部分,得到一个工件如图②.对于这个工件.俯视图、主视图依次是
.
19.用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示,则搭出这个几何体至少需要
个小立方体,最多需要
个小立方体.
20.如图所示,是由若干相同大小的小立方体组成的立体图形的三视图,请在右边的立体图形中画出所缺少的小立方体
.
三.解答题
21.1805年,法军在拿破仑的率领下与德军在莱茵河畔激战.德军在莱茵河北岸Q处,如图所示,因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸的点O处调整好自己的帽子,使视线恰好擦着帽舌边缘看到敌军兵营Q处,然后后退到B点,这是他的视点恰好能落在0处,于是他命令部下测量他脚站的B处与O点之间的距离,并下令按这个距离炮轰敌营,法军能命中目标吗?请说明理由.
22.小明和小红并排站立在阳光下,小明身高1.75米,他的影长2.0米,小红比小明矮7厘米,此时小红的影长是多少米?
23.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
24.如图,一路灯距地面5.6米,身高1.6米的小方从距离灯的底部(点O)5米的A处,沿OA所在的直线行走到点C时,人影长度增长3米,求小方行走的路程.
25.如图是由8个相同的小立方体组成的几何体,请在下列方框内画出它的三视图.
26.如图①是一张长为18cm,宽为12cm的长方形硬纸板.把它的四个角都剪去一个边长为xcm的小正方形,然后把它折成一个无盖的长方体盒子(如图②),请回答下列问题:
(1)折成的无盖长方体盒子的容积V=
cm3;(用含x的代数式表示即可,不需化简)
(2)请完成下表,并根据表格回答,当x取什么正整数时,长方体盒子的容积最大?
x/cm
1
2
3
4
5
V/cm3
160
216
80
(3)从正面看折成的长方体盒子,它的形状可能是正方形吗?如果是正方形,求出x的值;如果不是正方形,请说明理由.
参考答案与试题解析
一.选择题
1.解:A、圆柱的左视图是矩形,故本选项错误;
B、圆锥的左视图是等腰三角形,故本选项正确;
C、三棱柱的左视图是矩形,故本选项错误;
D、长方体的左视图是矩形,故本选项错误.
故选:B.
2.解:从左边看,是一列两个小正方形.
故选:D.
3.解:从上面看共有两层,底层右边是1个小正方形,上层有2个小正方形.
故选:D.
4.解:当他远离路灯走向B处时,光线与地面的夹角越来越小,小明在地面上留下的影子越来越长,
所以他在走过一盏路灯的过程中,其影子的长度逐渐变长,
故选:A.
5.解:按照时间的先后顺序排列正确的是(4)、(3)、(2)、(1).
故选:C.
6.解:根据平行投影的概念可知,素描画不是光线照射形成的.
故选:B.
7.解:设图书馆为点E,由题意得,EC=ED,EC⊥ED,
∵∠AEC+∠DEB=180°﹣90°,∠DEB+∠D=90°,
∴∠AEC=∠D,∠A=∠B=90°,
在Rt△AEC和Rt△BDE中,
,
∴△AEC≌△BDE(AAS),
∴AC=BE=10,
∴AE=AB﹣BE=22﹣10=12,
故选:A.
8.解:A、圆柱的左视图和俯视图分别为长方形,圆,故A选项不符合题意;
B、球的左视图和俯视图都是圆,故B选项符合题意;
C、圆锥的左视图和俯视图分别为等腰三角形,圆及圆心,故C选项不符合题意;
D、圆台的左视图和俯视图分别为梯形,圆环,故D选项不符合题意.
故选:B.
9.解:该几何体的左视图如图所示:.
故选:A.
10.解:如图所示的一个三棱柱,它的主视图和左视图是.
故选:B.
二.填空题
11.解:投影可分为平行投影和中心投影;一个立体图形,共有三种视图,
故答案为:平行投影,中心投影,三.
12.解:把大型会场、体育看台、电影院建为阶梯形状,是为了使后面的观众有更大的视野,从而减小盲区.
13.解:由题意可知,该图形是一个长方体的表面展开图,A面对应F面,B面对应D面,C面对应E面,
∵面F在前面,
∴面A在后面,
∵面B在左面,
∴面D在右面,
∴E在下面,C在上面.
故答案为:C.
14.解:球体的主视图与左视图都为圆.
故答案为:圆球(答案不唯一).
15.解:主视图如图所示,
∵由6个棱长均为1的正方体组成的几何体,
∴主视图的面积为5×12=5,
故答案为5.
16.解:∵BC∥DE,
∴△ABC∽△ADE,
∴,
∵BC=1.2,
∴DE=2,
∴E(4,0).
故答案为:(4,0).
17.解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED?FD,
代入数据可得DC2=64,
DC=8;
故答案为:8m.
18.解:从上面看可得到一个等边三角形,从正面看可得到一个直角梯形,所以俯视图、主视图依次是b、a.
故答案为:b、a.
19.解:∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体;最多有5个正方体,
∴该组合几何体最少有5+2=7个正方体,最多有5+5=10个正方体.
故答案为:7,10.
20.解:
三.解答题
21.解:根据题意知AB=PO,∠A=∠P,
又∵AB⊥BO,PO⊥BQ,
∴∠ABO=∠POQ=90°,
在△ABO和△POQ中,
,
∴△ABO≌△POQ(ASA),
∴BO=OQ,
故按这个距离炮轰敌营,法军能命中目标.
22.解:设小红的影长是x米,
根据题意得=,
解得x=1.92.
答:小红的影长是1.92米.
23.解:
24.解:∵AE⊥OD,GO⊥OD,
∴EA∥GO,
∴△AEB∽△OGB,
∴=,
∴=,
解得AB=2(m);
∵OA所在的直线行走到点C时,人影长度增长3米,
∴DC=5(m),
同理可得△DFC∽△DGO,
∴=,
即=,
解得AC=7.5(m).
答:小方行走的路程AC为7.5m.
25.解:
26.解:(1)由题意得,长方体盒子的长(18﹣2x)、宽(12﹣2x)、高x,因此体积为:(18﹣2x)?(12﹣2x)?x,
故答案为:(18﹣2x)?(12﹣2x)?x,
(2)把x=2代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=14×8×2=224,
把x=4代入(18﹣2x)?(12﹣2x)?x得,(18﹣2x)?(12﹣2x)?x=10×4×4=160,
故答案为:224,160;
(3)它的形状不可能是正方形,
当18﹣2x=x时,即x=6,而当x=6时,图①的长边变为0,因此折不成长方体,故从正面看是正方形是不可能的.
