2020-2021学年沪科新版八年级上册数学《第13章 三角形中的边角关系、命题与证明》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年沪科新版八年级上册数学《第13章 三角形中的边角关系、命题与证明》单元测试卷(word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览



文档简介
2020-2021学年沪科新版八年级上册数学《第13章
三角形中的边角关系、命题与证明》单元测试卷
一.选择题
1.图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
2.如图所示,其中三角形的个数是( )
A.2个
B.3个
C.4个
D.5个
3.下列命题是真命题的是( )
A.如果a2=b2,那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.平面内,垂直于同一条直线的两条直线平行
4.如图,BD是△ABC的中线,点E、F分别为BD、CE的中点,若△AEF的面积为3.则△ABC的面积是( )
A.9
B.10
C.11
D.12
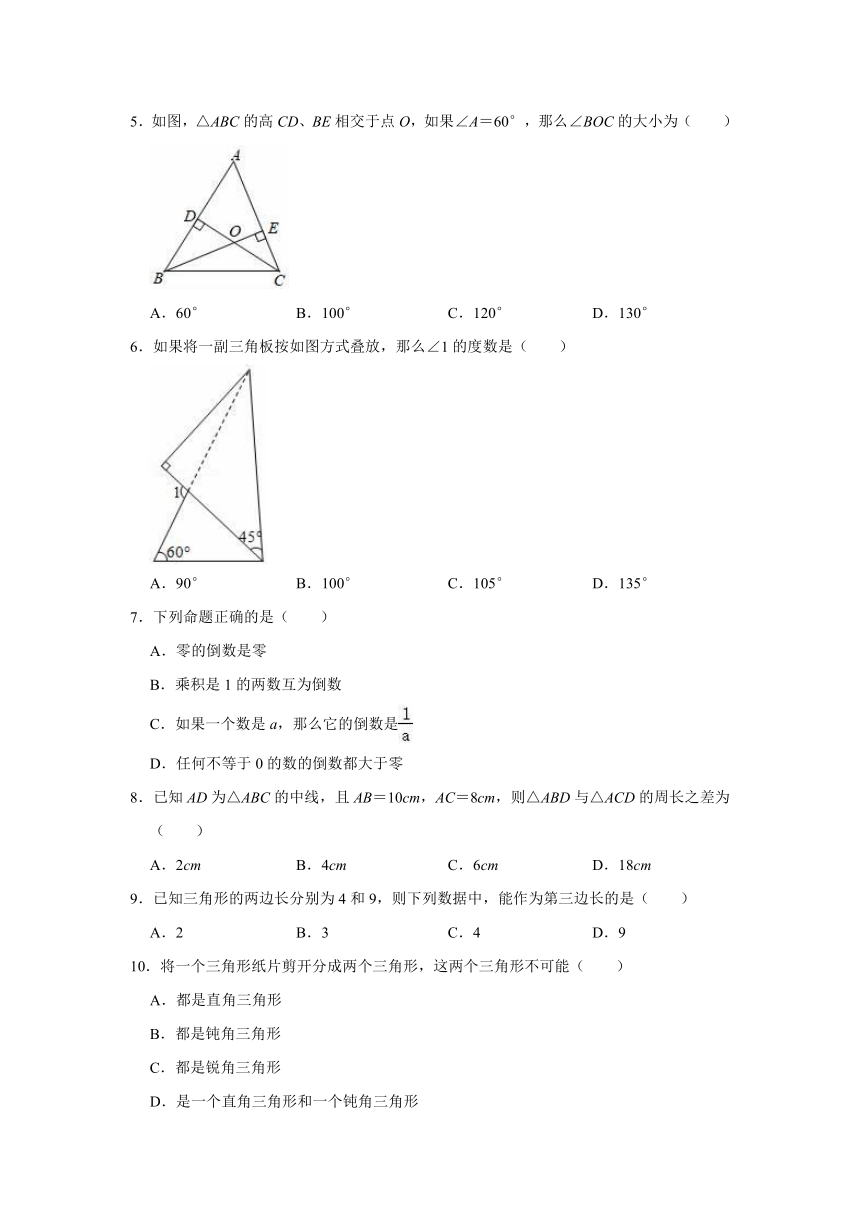
5.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60°
B.100°
C.120°
D.130°
6.如果将一副三角板按如图方式叠放,那么∠1的度数是( )
A.90°
B.100°
C.105°
D.135°
7.下列命题正确的是( )
A.零的倒数是零
B.乘积是1的两数互为倒数
C.如果一个数是a,那么它的倒数是
D.任何不等于0的数的倒数都大于零
8.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm
B.4cm
C.6cm
D.18cm
9.已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2
B.3
C.4
D.9
10.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
二.填空题
11.一副三角尺如图摆放,D是BC延长线上一点,E是AC上一点,∠B=∠EDF=90°,∠A=30°,∠F=45°,若EF∥BC,则∠CED等于
度.
12.如图△ABC中,AB=21,AC=20,AD为中线,则△ABD与△ACD的周长之差=
.
13.若三角形三条边长分别是1、a、3(其中a为整数),则a=
.
14.三角形周长为12,且三边a,b,c有如下关系,c=b﹣1,b=a﹣1,则a=
,b=
,c=
.
15.如图,直角ABC的周长为2008,在其内部有五个小直角三角形,则这五个小直角三角形的周长为
.
16.如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2;使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,….按此规律,要使得到的三角形的面积超过2021,最少经过
次操作.
17.命题“等角的补角相等”写成“如果…,那么…”
.
18.如图,点D在AB上,点E在AC上,BE、CD相交于点O,∠A=40°,∠C=30°,∠BOD=100°.则∠B=
°.
19.“锐角与钝角是互为补角”是
命题.(填写“真”或“假”)
20.图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)
(1)图2有
个三角形;图3中有
个三角形
(2)按上面方法继续下去,第20个图有
个三角形;第n个图中有
个三角形.(用n的代数式表示结论)
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.在平面直角坐标系中,O为坐标原点,点A的坐标(a,3),点B坐标为(b,6),若a,b的方程组满足
(1)当m=﹣3时,点A的坐标为
;点B的坐标为
.
(2)当这个方程组的解a,b满足,求m的取值范围;
(3)若AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,则四边形ACDB的面积为
.
23.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
24.如图,武汉有三个车站A、B、C成三角形,一辆公共汽车从B站前往到C站.
(1)当汽车运动到点D点时,刚好BD=CD,连接线段AD,AD这条线段是什么线段?这样的线段在△ABC中有几条呢?此时有面积相等的三角形吗?
(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段呢?在△ABC中,这样的线段又有几条呢?
(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?这样的线段在△ABC中有几条?
25.已知a、b、c是三角形的三边长,
①化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|;
②若a+b=11,b+c=9,a+c=10,求这个三角形的各边.
26.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,求∠CHD的度数.
27.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有
个三角形.
参考答案与试题解析
一.选择题
1.解:从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角.
故选:D.
2.解:△ABE,△DEC,△BEC,△ABC,△DBC共5个.故选D.
3.解:A、如果a2=b2,那么a=±b,故错误,是假命题;
B、两直线平行,同位角才相等,故错误,是假命题;
C、相等的两个角不一定是对顶角,故错误,是假命题;
D、平面内,垂直于同一条直线的两条直线平行,正确,是真命题,
故选:D.
4.解:∵F是CE的中点,△AEF的面积为3,
∴S△ACE=2S△AEF=6,
∵E是BD的中点,
∴S△ADE=S△ABE,S△CDE=S△BCE,
∴S△ACE=S△ADE+S△CDE=S△ABE+S△BCE=S△ABC,
∴△ABC的面积=12.
故选:D.
5.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
6.解:如图所示:由题意可得,∠2=90°﹣45°=45°,
则∠1=∠2+60°=45°+60°=105°.
故选:C.
7.解:A、零没有倒数,本选项说法错误;
B、乘积是1的两数互为倒数,本选项说法正确;
C、如果a=0,则a没有倒数,本选项说法错误;
D、﹣2的倒数是﹣,﹣<0,则任何不等于0的数的倒数都大于零说法错误;
故选:B.
8.解:∵AD为中线,
∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC,
∵AB=10,AC=8,
∴△ABD与△ACD的周长之差=10﹣8=2(cm).
故选:A.
9.解:设这个三角形的第三边为x.
根据三角形的三边关系定理,得:9﹣4<x<9+4,
解得5<x<13.
故选:D.
10.解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:C.
二.填空题
11.解:∵∠B=90°,∠A=30°,
∴∠ACB=60°.
∵∠EDF=90°,∠F=45°,
∴∠DEF=45°.
∵EF∥BC,
∴∠CEF=∠ACB=60°,
∴∠CED=∠CEF﹣∠DEF=60°﹣45°=15°.
故答案为:15.
12.解:∵AD为△ABC的中线,
∴BD=CD,
∴△ABD的周长﹣△ACD的周长=(AB+BD+AD)﹣(AC+CD+AD)=AB﹣AC=1,
故答案为:1.
13.解:∵三角形的两边长分别为1和3,
∴第三边长a的取值范围是:3﹣1<a<3+1,
即:2<a<4,
∴a的值为3,
故答案为:3.
14.解:∵c=b﹣1,b=a﹣1,
∴c=a﹣1﹣1=a﹣2,
又∵a+b+c=12,
则a+a﹣1+a﹣2=12,
解得:a=5,
则b=a﹣1=4,c=a﹣2=3,
故答案为:5,4,3.
15.解:∵五个小直角三角形与大三角形相似,
∴对应边的比相等,
∵五个小三角形的斜边长的和等于大三角形的斜边长,
∴五个小三角形的周长的和等于大三角形的周长为2008.
16.解:连接A1C,
∵AB=A1B,
∴△ABC与△A1BC的面积相等,
∵△ABC面积为1,
∴S△A1BC=1.
∵BB1=2BC,
∴S△A1B1B=2S△A1BC=2,
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可证△A2B2C2的面积=7×△A1B1C1的面积=49,
第三次操作后的面积为7×49=343,
第四次操作后的面积为7×343=2401.
故按此规律,要使得到的三角形的面积超过2021,最少经过4次操作.
故答案为:4.
17.解:命题“等角的补角相等”写成“如果…,那么…”是:如果两个角相等,那么它们的补角相等,
故答案为:如果两个角相等,那么它们的补角相等.
18.解:∵∠A=40°,∠C=30°,
∴∠BDO=∠A+∠C=70°;
∵∠BOD=100°,
∴∠B=180°﹣∠BDO﹣∠BOD=10°.
故答案为:10.
19.解:30°的锐角和100°的钝角的和为130°,不是互为补角,
所以“锐角与钝角是互为补角”是假命题.
故答案为:假.
20.解:(1)图2有4个三角形;图3中有7个三角形;
(2)按上面方法继续下去,可以得到(4)比(3)增加了4个三角形,
依此类推,第20个图有3×20﹣2=58个三角形;第n个图中有(3n﹣2)个三角形.
故答案为:(1)4;7;(2)58;(3n﹣2)
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:(1)将原方程组整理可得,
解得:,
当m=﹣3时,a=﹣4、b=﹣2,
∴点A坐标为(﹣4,3)、点B坐标为(﹣2,6),
故答案为:(﹣4,3)、(﹣2,6);
(2)将代入不等式组,得:
解得:2≤m≤5;
(3)由(1)知A(m﹣1,3)、B(m+1,6),
∴CD=m+1﹣(m﹣1)=2,AC=3、BD=6,
则四边形ACDB的面积为×CD×(AC+BD)=×2×9=9,
故答案为:9.
23.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
24.解:(1)AD是△ABC中BC边上的中线,三角形中有三条中线.此时△ABD与△ADC的面积相等.
(2)AE是△ABC中∠BAC的角平分线,三角形上角平分线有三条.
(3)AF是△ABC中BC边上的高线,高线有时在三角形外部,三角形中有三条高线.
25.解:(1)∵a、b、c是三角形的三边长,
∴a﹣b﹣c<0,b﹣c﹣a<0,c﹣a﹣b<0,
∴|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|=﹣a+b+c﹣b+c+a﹣c+a+b=a+b+c;
(2)∵a+b=11①,b+c=9②,a+c=10③,
∴由①﹣②,得
a﹣c=2,④
由③+④,得2a=12,
∴a=6,
∴b=11﹣6=5,
∴c=10﹣6=4.
26.解:延长CH交AB于F,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,
∵∠ACB=60°,∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
27.解:(1)
连接个数
1
2
3
4
5
6
出现三角形个数
3
6
10
15
21
28
(2)8个点;
(3)1+2+3+…+(n+1)
=
[1+2+3+…+(n+1)+1+2+3+…+(n+1)]
=(n+1)(n+2).
故答案为(n+1)(n+2).
三角形中的边角关系、命题与证明》单元测试卷
一.选择题
1.图中的三角形被木板遮住了一部分,这个三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.以上都有可能
2.如图所示,其中三角形的个数是( )
A.2个
B.3个
C.4个
D.5个
3.下列命题是真命题的是( )
A.如果a2=b2,那么a=b
B.如果两个角是同位角,那么这两个角相等
C.相等的两个角是对顶角
D.平面内,垂直于同一条直线的两条直线平行
4.如图,BD是△ABC的中线,点E、F分别为BD、CE的中点,若△AEF的面积为3.则△ABC的面积是( )
A.9
B.10
C.11
D.12
5.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60°
B.100°
C.120°
D.130°
6.如果将一副三角板按如图方式叠放,那么∠1的度数是( )
A.90°
B.100°
C.105°
D.135°
7.下列命题正确的是( )
A.零的倒数是零
B.乘积是1的两数互为倒数
C.如果一个数是a,那么它的倒数是
D.任何不等于0的数的倒数都大于零
8.已知AD为△ABC的中线,且AB=10cm,AC=8cm,则△ABD与△ACD的周长之差为( )
A.2cm
B.4cm
C.6cm
D.18cm
9.已知三角形的两边长分别为4和9,则下列数据中,能作为第三边长的是( )
A.2
B.3
C.4
D.9
10.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形
B.都是钝角三角形
C.都是锐角三角形
D.是一个直角三角形和一个钝角三角形
二.填空题
11.一副三角尺如图摆放,D是BC延长线上一点,E是AC上一点,∠B=∠EDF=90°,∠A=30°,∠F=45°,若EF∥BC,则∠CED等于
度.
12.如图△ABC中,AB=21,AC=20,AD为中线,则△ABD与△ACD的周长之差=
.
13.若三角形三条边长分别是1、a、3(其中a为整数),则a=
.
14.三角形周长为12,且三边a,b,c有如下关系,c=b﹣1,b=a﹣1,则a=
,b=
,c=
.
15.如图,直角ABC的周长为2008,在其内部有五个小直角三角形,则这五个小直角三角形的周长为
.
16.如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2;使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,….按此规律,要使得到的三角形的面积超过2021,最少经过
次操作.
17.命题“等角的补角相等”写成“如果…,那么…”
.
18.如图,点D在AB上,点E在AC上,BE、CD相交于点O,∠A=40°,∠C=30°,∠BOD=100°.则∠B=
°.
19.“锐角与钝角是互为补角”是
命题.(填写“真”或“假”)
20.图1是一个三角形,分别连接这个三角形三边的中点得到图2;再分别连接图2中间小三角形的中点,得到图3.(若三角形中含有其它三角形则不记入)
(1)图2有
个三角形;图3中有
个三角形
(2)按上面方法继续下去,第20个图有
个三角形;第n个图中有
个三角形.(用n的代数式表示结论)
三.解答题
21.如图,已知==,△ABC的周长是14cm,求BC的长.
22.在平面直角坐标系中,O为坐标原点,点A的坐标(a,3),点B坐标为(b,6),若a,b的方程组满足
(1)当m=﹣3时,点A的坐标为
;点B的坐标为
.
(2)当这个方程组的解a,b满足,求m的取值范围;
(3)若AC⊥x轴,垂足为C,BD⊥x轴,垂足为D,则四边形ACDB的面积为
.
23.如图所示,图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.
24.如图,武汉有三个车站A、B、C成三角形,一辆公共汽车从B站前往到C站.
(1)当汽车运动到点D点时,刚好BD=CD,连接线段AD,AD这条线段是什么线段?这样的线段在△ABC中有几条呢?此时有面积相等的三角形吗?
(2)汽车继续向前运动,当运动到点E时,发现∠BAE=∠CAE,那么AE这条线段是什么线段呢?在△ABC中,这样的线段又有几条呢?
(3)汽车继续向前运动,当运动到点F时,发现∠AFB=∠AFC=90°,则AF是什么线段?这样的线段在△ABC中有几条?
25.已知a、b、c是三角形的三边长,
①化简:|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|;
②若a+b=11,b+c=9,a+c=10,求这个三角形的各边.
26.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,求∠CHD的度数.
27.如图,△ABC中,A1,A2,A3,…,An为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…
(1)完成下表:
连接个数
出现三角形个数
(2)若出现了45个三角形,则共连接了多少个点?
(3)若一直连接到An,则图中共有
个三角形.
参考答案与试题解析
一.选择题
1.解:从图中,只能看到一个角是锐角,其它的两个角中,可以都是锐角或有一个钝角或有一个直角.
故选:D.
2.解:△ABE,△DEC,△BEC,△ABC,△DBC共5个.故选D.
3.解:A、如果a2=b2,那么a=±b,故错误,是假命题;
B、两直线平行,同位角才相等,故错误,是假命题;
C、相等的两个角不一定是对顶角,故错误,是假命题;
D、平面内,垂直于同一条直线的两条直线平行,正确,是真命题,
故选:D.
4.解:∵F是CE的中点,△AEF的面积为3,
∴S△ACE=2S△AEF=6,
∵E是BD的中点,
∴S△ADE=S△ABE,S△CDE=S△BCE,
∴S△ACE=S△ADE+S△CDE=S△ABE+S△BCE=S△ABC,
∴△ABC的面积=12.
故选:D.
5.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
6.解:如图所示:由题意可得,∠2=90°﹣45°=45°,
则∠1=∠2+60°=45°+60°=105°.
故选:C.
7.解:A、零没有倒数,本选项说法错误;
B、乘积是1的两数互为倒数,本选项说法正确;
C、如果a=0,则a没有倒数,本选项说法错误;
D、﹣2的倒数是﹣,﹣<0,则任何不等于0的数的倒数都大于零说法错误;
故选:B.
8.解:∵AD为中线,
∴BD=CD,
∴△ABD与△ACD的周长之差=(AB+AD+BD)﹣(AC+AD+CD)=AB﹣AC,
∵AB=10,AC=8,
∴△ABD与△ACD的周长之差=10﹣8=2(cm).
故选:A.
9.解:设这个三角形的第三边为x.
根据三角形的三边关系定理,得:9﹣4<x<9+4,
解得5<x<13.
故选:D.
10.解:如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角是邻补角,不可能都是锐角,故这两个三角形不可能都是锐角三角形.
综上所述,将一个三角形剪成两三角形,这两个三角形不可能都是锐角三角形.
故选:C.
二.填空题
11.解:∵∠B=90°,∠A=30°,
∴∠ACB=60°.
∵∠EDF=90°,∠F=45°,
∴∠DEF=45°.
∵EF∥BC,
∴∠CEF=∠ACB=60°,
∴∠CED=∠CEF﹣∠DEF=60°﹣45°=15°.
故答案为:15.
12.解:∵AD为△ABC的中线,
∴BD=CD,
∴△ABD的周长﹣△ACD的周长=(AB+BD+AD)﹣(AC+CD+AD)=AB﹣AC=1,
故答案为:1.
13.解:∵三角形的两边长分别为1和3,
∴第三边长a的取值范围是:3﹣1<a<3+1,
即:2<a<4,
∴a的值为3,
故答案为:3.
14.解:∵c=b﹣1,b=a﹣1,
∴c=a﹣1﹣1=a﹣2,
又∵a+b+c=12,
则a+a﹣1+a﹣2=12,
解得:a=5,
则b=a﹣1=4,c=a﹣2=3,
故答案为:5,4,3.
15.解:∵五个小直角三角形与大三角形相似,
∴对应边的比相等,
∵五个小三角形的斜边长的和等于大三角形的斜边长,
∴五个小三角形的周长的和等于大三角形的周长为2008.
16.解:连接A1C,
∵AB=A1B,
∴△ABC与△A1BC的面积相等,
∵△ABC面积为1,
∴S△A1BC=1.
∵BB1=2BC,
∴S△A1B1B=2S△A1BC=2,
同理可得,S△C1B1C=2,S△AA1C=2,
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7;
同理可证△A2B2C2的面积=7×△A1B1C1的面积=49,
第三次操作后的面积为7×49=343,
第四次操作后的面积为7×343=2401.
故按此规律,要使得到的三角形的面积超过2021,最少经过4次操作.
故答案为:4.
17.解:命题“等角的补角相等”写成“如果…,那么…”是:如果两个角相等,那么它们的补角相等,
故答案为:如果两个角相等,那么它们的补角相等.
18.解:∵∠A=40°,∠C=30°,
∴∠BDO=∠A+∠C=70°;
∵∠BOD=100°,
∴∠B=180°﹣∠BDO﹣∠BOD=10°.
故答案为:10.
19.解:30°的锐角和100°的钝角的和为130°,不是互为补角,
所以“锐角与钝角是互为补角”是假命题.
故答案为:假.
20.解:(1)图2有4个三角形;图3中有7个三角形;
(2)按上面方法继续下去,可以得到(4)比(3)增加了4个三角形,
依此类推,第20个图有3×20﹣2=58个三角形;第n个图中有(3n﹣2)个三角形.
故答案为:(1)4;7;(2)58;(3n﹣2)
三.解答题
21.解:∵==,
设AB为5x,BD为2x,AC为5y,CD为2y,
∵△ABC的周长是14cm,
∴5x+2x+5y+2y=14,
解得:x+y=2,
所以BC=2(x+y)=4.
22.解:(1)将原方程组整理可得,
解得:,
当m=﹣3时,a=﹣4、b=﹣2,
∴点A坐标为(﹣4,3)、点B坐标为(﹣2,6),
故答案为:(﹣4,3)、(﹣2,6);
(2)将代入不等式组,得:
解得:2≤m≤5;
(3)由(1)知A(m﹣1,3)、B(m+1,6),
∴CD=m+1﹣(m﹣1)=2,AC=3、BD=6,
则四边形ACDB的面积为×CD×(AC+BD)=×2×9=9,
故答案为:9.
23.解:图中共有7个,△AEF,△ADE,△DEB,△ABF,△BCF,△ABC,△ABE,以E为顶点的角是∠AEF,∠AED,∠DEB,∠DEF,∠AEB,∠BEF.
24.解:(1)AD是△ABC中BC边上的中线,三角形中有三条中线.此时△ABD与△ADC的面积相等.
(2)AE是△ABC中∠BAC的角平分线,三角形上角平分线有三条.
(3)AF是△ABC中BC边上的高线,高线有时在三角形外部,三角形中有三条高线.
25.解:(1)∵a、b、c是三角形的三边长,
∴a﹣b﹣c<0,b﹣c﹣a<0,c﹣a﹣b<0,
∴|a﹣b﹣c|+|b﹣c﹣a|+|c﹣a﹣b|=﹣a+b+c﹣b+c+a﹣c+a+b=a+b+c;
(2)∵a+b=11①,b+c=9②,a+c=10③,
∴由①﹣②,得
a﹣c=2,④
由③+④,得2a=12,
∴a=6,
∴b=11﹣6=5,
∴c=10﹣6=4.
26.解:延长CH交AB于F,
在△ABC中,三边的高交于一点,所以CF⊥AB,
∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,
∵∠ACB=60°,∴∠BCF=45°
在△CDH中,三内角之和为180°,
∴∠CHD=45°,
27.解:(1)
连接个数
1
2
3
4
5
6
出现三角形个数
3
6
10
15
21
28
(2)8个点;
(3)1+2+3+…+(n+1)
=
[1+2+3+…+(n+1)+1+2+3+…+(n+1)]
=(n+1)(n+2).
故答案为(n+1)(n+2).
