2020-2021学年沪科新版九年级上册数学《第22章 相似形》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年沪科新版九年级上册数学《第22章 相似形》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 377.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 21:56:22 | ||
图片预览




文档简介
2020-2021学年沪科新版九年级上册数学《第22章
相似形》单元测试卷
一.选择题
1.若=,则等于( )
A.
B.
C.
D.
2.已知=,则的值为( )
A.
B.
C.
D.
3.下列四组线段中,不构成比例线段的一组是( )
A.1cm,2cm,3cm,6cm
B.2cm,3cm,4cm,6cm
C.1cm,
cm,
cm,
cm
D.1cm,2cm,3cm,4cm
4.下列各组图形一定相似的是( )
A.两个矩形
B.两个等边三角形
C.各有一角是80°的两个等腰三角形
D.任意两个菱形
5.已知,那么下列等式中,不成立的是( )
A.
B.
C.(y≠﹣4a)
D.4x=3y
6.如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F,则图中与△ABD相似的是( )
A.△ABC
B.△ABF
C.△BFD
D.△AEF
7.如图,在△ABC中,D为AB上一点,若AC2=AD?AB,则( )
A.△ADC∽△CBD
B.△BDC∽△BCA
C.△ADC∽△ACB
D.无法判断
8.若△ABC∽△ADE,AB=9,AC=6,AD=3,则EC的长是( )
A.2
B.3
C.4
D.5
9.如图,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形以此类推,第2020个黄金三角形的周长( )
A.k2018
B.k2019
C.
D.k2019(2+k)
10.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( )
A.2
B.
C.3
D.
二.填空题
11.如果x:y=1:2,那么=
.
12.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=1,则AD=
.
13.已知△ABC的三边分别是5,6,7,则与它相似△A′B′C′的最短边为10,则△A′B′C′的周长是
.
14.若x:y=5:2,则(x+y):y的值是
.
15.已知线段AB,点P是线段AB的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形的面积为S2,则S1
S2(填<、≤、=、>或≥).
16.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为
cm.
17.如图,∠B=∠D,请你添加一个条件,使得△ABC∽△ADE,这个条件可以是
.
18.如果=,那么=
.
19.在1:40000的地图上,村犀路的距离是7厘米,则实际距离是
千米.
20.如图,在△ABC中,P为AB上的一点,补充条件,能使△APC∽△ACB,这个条件可以是
.(写出一个即可)
三.解答题
21.已知==,且2x+3y﹣z=18,求x,y,z的值.
22.已知,求m的值.
23.已知,求的值.
24.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
25.已知==2,求和的值.
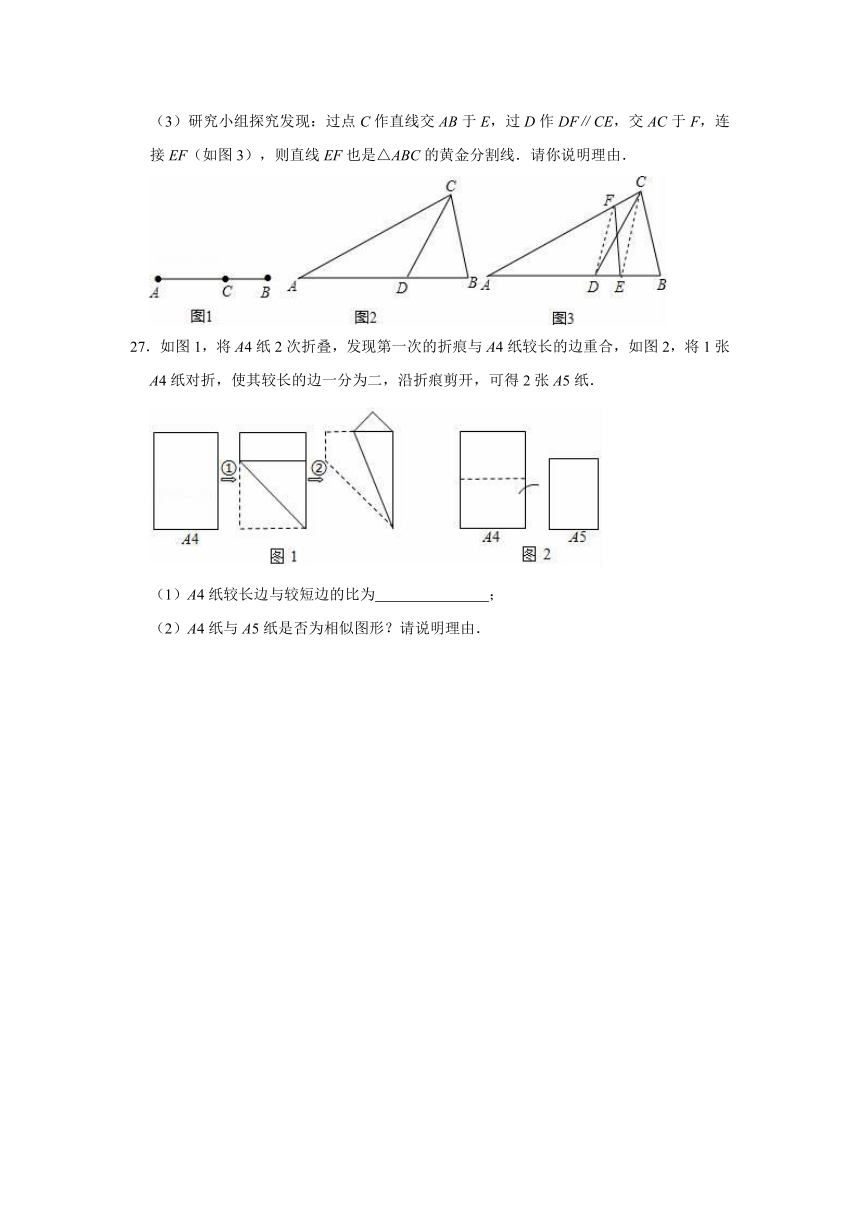
26.阅读理解:
如图1,点C将线段AB分成两部分,若=,则点C为线段AB的黄金分割点.
某研究学习小组,由黄金分割点联想到“黄金分割线”,而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果=,那么称直线l为该图形的黄金分割线.
问题解决:
如图2,在△ABC中,若点D是AB的黄金分割点.
(1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组探究发现:过点C作直线交AB于E,过D作DF∥CE,交AC于F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.
27.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为
;
(2)A4纸与A5纸是否为相似图形?请说明理由.
参考答案与试题解析
一.选择题
1.解:∵=,
∴a=b,
则==.
故选:A.
2.解:由=,得==.
故选:D.
3.解:A、1:2=3:6,即1cm,2cm,3cm,6cm成比例;
B、2:3=4:6,即2cm,3cm,4cm,6cm成比例;
C、1:=:,即1cm,
cm,
cm,
cm成比例;
D、四条线段中,任意两条的比都不相等,因而不成比例.
故选:D.
4.解:两个矩形对应边的比不一定相等,故不一定相似;
两个等边三角形相似对应边的比相等,对应角相等,一定相似;
各有一角是80°的两个等腰三角形对应角不一定相等,故不一定相似;
任意两个菱形对应角不一定相等,故不一定相似;
故选:B.
5.解:A、∵,
∴=,此选项正确,不合题意;
B、∵,
∴=﹣,此选项错误,符合题意;
C、∵,
∴=,此选项正确,不合题意;
D、∵,
∴4x=3y,此选项正确,不合题意;
故选:B.
6.解:在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,
∴△ABE∽△ACB,
∴∠AEB=∠ABC,
∵AD平分∠BAC,
∴∠BAD=∠EAF,
∴△ABD∽△AEF.
故选:D.
7.解:∵AC2=AD?AB,
∴,
∵∠A=∠A,且∠A为AD、AC和AB、AC的夹角,
∴△ADC∽△ACB.
故选:C.
8.解:设EC=x,
∵AC=6,
∴AE=6﹣x,
∵△ABC∽△ADE,
∴,
∴,
解得:x=4,
故选:C.
9.解:∵AB=AC=1,
∴△ABC的周长为2+k;
△BCD的周长为k+k+k2=k(2+k);
△CDE的周长为k2+k2+k3=k2(2+k);
依此类推,
第n个黄金三角形的周长为kn﹣1(2+k),
∴第2020个黄金三角形的周长为k2019(2+k).
故选:D.
10.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
二.填空题
11.解:
+1=+1,即=.
故答案为:.
12.解:∵△ABC的两条中线AD,BE交于点G,
∴BD=CD,AE=CE,
∵EF∥CD,
∴==1,即AF=FD,
∴EF为△ADC的中位线,
∴EF=CD,
∴EF=BD,
∵EF∥BD,
∴==,
∴DG=2FG=2,
∴FD=2+1=3,
∴AD=2FG=6.
故答案为6.
13.解:∵△ABC∽△A′B′C′,△ABC的三边分别是5,6,7,△A′B′C′的最短边为10,
∴相似比是:=,
∴△A′B′C′的另外两条边是6×2=12,7×2=14,
∴△A′B′C′的周长是:10+12+14=36,
故答案为:36.
14.解:由合比性质,得
==,
故答案为:.
15.解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB?AB,
则S1:S2=AP2:(PB?AB)=1,即S1=S2.
故答案为:=.
16.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
17.解:∵∠B=∠D,
∴添加∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或=,可证△ABC∽△ADE.
故答案为:∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或=.
18.解:∵=,则x=y,
∴===.
故答案为:.
19.解:因为实际距离=图上距离÷比例尺,
则:7÷=280000(厘米)=2800(米)=2.8千米;
答:这两地之间的实际距离是2.8千米.
故答案为:2.8.
20.解:∵∠PAC=∠CAB,
∴当∠ACP=∠B时,△ACP∽△APC,
故答案为:∠ACP=∠B(答案不唯一)
三.解答题
21.解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
22.解:由可知:
x+y=mz,y+z=mx,z+x=my.
这几式相加可得:2(x+y+z)=m(x+y+z),
当x+y+z≠0时,有m=2,
当x+y+z=0时,有x+y=﹣z,y+z=﹣x,x+z=﹣y,m=﹣1.
故m=2或﹣1.
23.解:设===k,
所以,a=3k,b=4k,c=5k,
则==.
24.解:∵a∥b∥c,
∴,
即,
解得:EF=.
25.解:因为==2,
可得:a=2b,c=2d,
所以=,=.
26.解:(1)直线CD是△ABC的黄金分割线.理由如下:
∵点D是AB的黄金分割点,
∴=,
∵=,=,
∴=,
∴直线CD是△ABC的黄金分割线;
(2)∵三角形的中线把AB分成相等的两条线段,即AD=BD,
∴=,==1,
∴三角形的中线不是该三角形的黄金分割线;
(3)∵DF∥CE,
∴S△FDE=S△FDC,S△DEC=S△FEC,
∴S△AEF=S△ADC,S四边形BEFC=S△BDC,
∵=,
∴=,
∴直线EF是△ABC的黄金分割线.
27.解:(1)如图1,
由折叠过程可以看到:第一次折叠,A与D重合,四边形ABDC为正方形,折痕BC为对角线,由勾股定理可得BC=AB;第二次折叠,第一次的折痕与A4纸较长的边重合,即BC与较长边重合.所以,较长边=AB.
∴A4纸较长边与较短边的比为:.
故答案为:.
(2)A4纸与A5纸是相似图形.理由:
∵A4纸较长边与较短边的比为:,
∴设A4纸较短边的长为a,则较长边为a.
∵由图2可知:A5纸的长边与A4纸的短边重合,短边等于A4纸的长边的一半,
∴A5纸的长边为a,短边为.
∴A5纸的长边与短边的比为:=.
∴A4纸较长边与较短边的比=A5纸的长边与短边的比.
又∵A4纸与A5纸的四个角均为直角,
∴A4纸与A5纸相似.
相似形》单元测试卷
一.选择题
1.若=,则等于( )
A.
B.
C.
D.
2.已知=,则的值为( )
A.
B.
C.
D.
3.下列四组线段中,不构成比例线段的一组是( )
A.1cm,2cm,3cm,6cm
B.2cm,3cm,4cm,6cm
C.1cm,
cm,
cm,
cm
D.1cm,2cm,3cm,4cm
4.下列各组图形一定相似的是( )
A.两个矩形
B.两个等边三角形
C.各有一角是80°的两个等腰三角形
D.任意两个菱形
5.已知,那么下列等式中,不成立的是( )
A.
B.
C.(y≠﹣4a)
D.4x=3y
6.如图,在△ABC中,D,E两点分别在BC,AC上,且AD平分∠BAC,若∠ABE=∠C,BE与AD相交于点F,则图中与△ABD相似的是( )
A.△ABC
B.△ABF
C.△BFD
D.△AEF
7.如图,在△ABC中,D为AB上一点,若AC2=AD?AB,则( )
A.△ADC∽△CBD
B.△BDC∽△BCA
C.△ADC∽△ACB
D.无法判断
8.若△ABC∽△ADE,AB=9,AC=6,AD=3,则EC的长是( )
A.2
B.3
C.4
D.5
9.如图,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形称为黄金三角形,已知腰AB=1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形以此类推,第2020个黄金三角形的周长( )
A.k2018
B.k2019
C.
D.k2019(2+k)
10.如图,点E是矩形ABCD的边CD上一点,作AF⊥BE于F,连接DF,若AB=6,DF=BC,则CE的长度为( )
A.2
B.
C.3
D.
二.填空题
11.如果x:y=1:2,那么=
.
12.如图,△ABC的两条中线AD,BE交于点G,EF∥BC交AD于点F.若FG=1,则AD=
.
13.已知△ABC的三边分别是5,6,7,则与它相似△A′B′C′的最短边为10,则△A′B′C′的周长是
.
14.若x:y=5:2,则(x+y):y的值是
.
15.已知线段AB,点P是线段AB的黄金分割点,AP>BP,设以AP为边的正方形的面积为S1,以PB、AB为边的矩形的面积为S2,则S1
S2(填<、≤、=、>或≥).
16.某课外活动小组的同学在研究某种植物标本(如图所示)时,测得叶片①最大宽度是8cm,最大长度是16cm;叶片②最大宽度是7cm,最大长度是14cm;叶片③最大宽度约为6.5cm,请你用所学数学知识估算叶片③的完整叶片的最大长度,结果约为
cm.
17.如图,∠B=∠D,请你添加一个条件,使得△ABC∽△ADE,这个条件可以是
.
18.如果=,那么=
.
19.在1:40000的地图上,村犀路的距离是7厘米,则实际距离是
千米.
20.如图,在△ABC中,P为AB上的一点,补充条件,能使△APC∽△ACB,这个条件可以是
.(写出一个即可)
三.解答题
21.已知==,且2x+3y﹣z=18,求x,y,z的值.
22.已知,求m的值.
23.已知,求的值.
24.如图,a∥b∥c,直线m,n与直线a,b,c分别相交于点A,B,C和点D,E,F.若AB=3,BC=5,DE=4,求EF的长.
25.已知==2,求和的值.
26.阅读理解:
如图1,点C将线段AB分成两部分,若=,则点C为线段AB的黄金分割点.
某研究学习小组,由黄金分割点联想到“黄金分割线”,而给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1、S2,如果=,那么称直线l为该图形的黄金分割线.
问题解决:
如图2,在△ABC中,若点D是AB的黄金分割点.
(1)研究小组猜想:直线CD是△ABC的黄金分割线,你认为对吗?为什么?
(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?
(3)研究小组探究发现:过点C作直线交AB于E,过D作DF∥CE,交AC于F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.
27.如图1,将A4纸2次折叠,发现第一次的折痕与A4纸较长的边重合,如图2,将1张A4纸对折,使其较长的边一分为二,沿折痕剪开,可得2张A5纸.
(1)A4纸较长边与较短边的比为
;
(2)A4纸与A5纸是否为相似图形?请说明理由.
参考答案与试题解析
一.选择题
1.解:∵=,
∴a=b,
则==.
故选:A.
2.解:由=,得==.
故选:D.
3.解:A、1:2=3:6,即1cm,2cm,3cm,6cm成比例;
B、2:3=4:6,即2cm,3cm,4cm,6cm成比例;
C、1:=:,即1cm,
cm,
cm,
cm成比例;
D、四条线段中,任意两条的比都不相等,因而不成比例.
故选:D.
4.解:两个矩形对应边的比不一定相等,故不一定相似;
两个等边三角形相似对应边的比相等,对应角相等,一定相似;
各有一角是80°的两个等腰三角形对应角不一定相等,故不一定相似;
任意两个菱形对应角不一定相等,故不一定相似;
故选:B.
5.解:A、∵,
∴=,此选项正确,不合题意;
B、∵,
∴=﹣,此选项错误,符合题意;
C、∵,
∴=,此选项正确,不合题意;
D、∵,
∴4x=3y,此选项正确,不合题意;
故选:B.
6.解:在△ABE与△ACB中,∠ABE=∠C,∠BAE=∠CAB,
∴△ABE∽△ACB,
∴∠AEB=∠ABC,
∵AD平分∠BAC,
∴∠BAD=∠EAF,
∴△ABD∽△AEF.
故选:D.
7.解:∵AC2=AD?AB,
∴,
∵∠A=∠A,且∠A为AD、AC和AB、AC的夹角,
∴△ADC∽△ACB.
故选:C.
8.解:设EC=x,
∵AC=6,
∴AE=6﹣x,
∵△ABC∽△ADE,
∴,
∴,
解得:x=4,
故选:C.
9.解:∵AB=AC=1,
∴△ABC的周长为2+k;
△BCD的周长为k+k+k2=k(2+k);
△CDE的周长为k2+k2+k3=k2(2+k);
依此类推,
第n个黄金三角形的周长为kn﹣1(2+k),
∴第2020个黄金三角形的周长为k2019(2+k).
故选:D.
10.解:过D作DH⊥AF于点H,延长DH与AB相交于点G,
∵四边形ABCD为矩形,
∴AD=BC,
∵DF=BC,
∴DA=DF,
∴AH=FH,
∵AF⊥BE,
∴DG∥BE,
∴AG=BG=,
∵矩形ABCD中,AB=DC=6,AB∥DC,
∴四边形BEDG为平行四边形,
∴DE=BG=3,
∴CE=CD﹣DE=6﹣3=3.
故选:C.
二.填空题
11.解:
+1=+1,即=.
故答案为:.
12.解:∵△ABC的两条中线AD,BE交于点G,
∴BD=CD,AE=CE,
∵EF∥CD,
∴==1,即AF=FD,
∴EF为△ADC的中位线,
∴EF=CD,
∴EF=BD,
∵EF∥BD,
∴==,
∴DG=2FG=2,
∴FD=2+1=3,
∴AD=2FG=6.
故答案为6.
13.解:∵△ABC∽△A′B′C′,△ABC的三边分别是5,6,7,△A′B′C′的最短边为10,
∴相似比是:=,
∴△A′B′C′的另外两条边是6×2=12,7×2=14,
∴△A′B′C′的周长是:10+12+14=36,
故答案为:36.
14.解:由合比性质,得
==,
故答案为:.
15.解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB?AB,
则S1:S2=AP2:(PB?AB)=1,即S1=S2.
故答案为:=.
16.解:根据叶片①②的最大长度和宽度,可得出这种植物的叶片的最大宽度:最大长度=1:2.由此可得出完整的叶片③的最大长度应是6.5×2=13cm.
故答案为:13.
17.解:∵∠B=∠D,
∴添加∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或=,可证△ABC∽△ADE.
故答案为:∠C=∠E或∠BAC=∠DAE或∠BAD=∠CAE或=.
18.解:∵=,则x=y,
∴===.
故答案为:.
19.解:因为实际距离=图上距离÷比例尺,
则:7÷=280000(厘米)=2800(米)=2.8千米;
答:这两地之间的实际距离是2.8千米.
故答案为:2.8.
20.解:∵∠PAC=∠CAB,
∴当∠ACP=∠B时,△ACP∽△APC,
故答案为:∠ACP=∠B(答案不唯一)
三.解答题
21.解:由==,得
y=,z=2x.
将y=,z=2x代入2x+3y﹣z=1中,得
2x+﹣2x=18.
解得x=4,y==6,z=2x=8.
22.解:由可知:
x+y=mz,y+z=mx,z+x=my.
这几式相加可得:2(x+y+z)=m(x+y+z),
当x+y+z≠0时,有m=2,
当x+y+z=0时,有x+y=﹣z,y+z=﹣x,x+z=﹣y,m=﹣1.
故m=2或﹣1.
23.解:设===k,
所以,a=3k,b=4k,c=5k,
则==.
24.解:∵a∥b∥c,
∴,
即,
解得:EF=.
25.解:因为==2,
可得:a=2b,c=2d,
所以=,=.
26.解:(1)直线CD是△ABC的黄金分割线.理由如下:
∵点D是AB的黄金分割点,
∴=,
∵=,=,
∴=,
∴直线CD是△ABC的黄金分割线;
(2)∵三角形的中线把AB分成相等的两条线段,即AD=BD,
∴=,==1,
∴三角形的中线不是该三角形的黄金分割线;
(3)∵DF∥CE,
∴S△FDE=S△FDC,S△DEC=S△FEC,
∴S△AEF=S△ADC,S四边形BEFC=S△BDC,
∵=,
∴=,
∴直线EF是△ABC的黄金分割线.
27.解:(1)如图1,
由折叠过程可以看到:第一次折叠,A与D重合,四边形ABDC为正方形,折痕BC为对角线,由勾股定理可得BC=AB;第二次折叠,第一次的折痕与A4纸较长的边重合,即BC与较长边重合.所以,较长边=AB.
∴A4纸较长边与较短边的比为:.
故答案为:.
(2)A4纸与A5纸是相似图形.理由:
∵A4纸较长边与较短边的比为:,
∴设A4纸较短边的长为a,则较长边为a.
∵由图2可知:A5纸的长边与A4纸的短边重合,短边等于A4纸的长边的一半,
∴A5纸的长边为a,短边为.
∴A5纸的长边与短边的比为:=.
∴A4纸较长边与较短边的比=A5纸的长边与短边的比.
又∵A4纸与A5纸的四个角均为直角,
∴A4纸与A5纸相似.
