2020-2021学年沪科新版七年级上册数学《第4章 直线与角》单元测试卷(word版含解析)
文档属性
| 名称 | 2020-2021学年沪科新版七年级上册数学《第4章 直线与角》单元测试卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-10 00:00:00 | ||
图片预览

文档简介
2020-2021学年沪科新版七年级上册数学《第4章
直线与角》单元测试卷
一.选择题
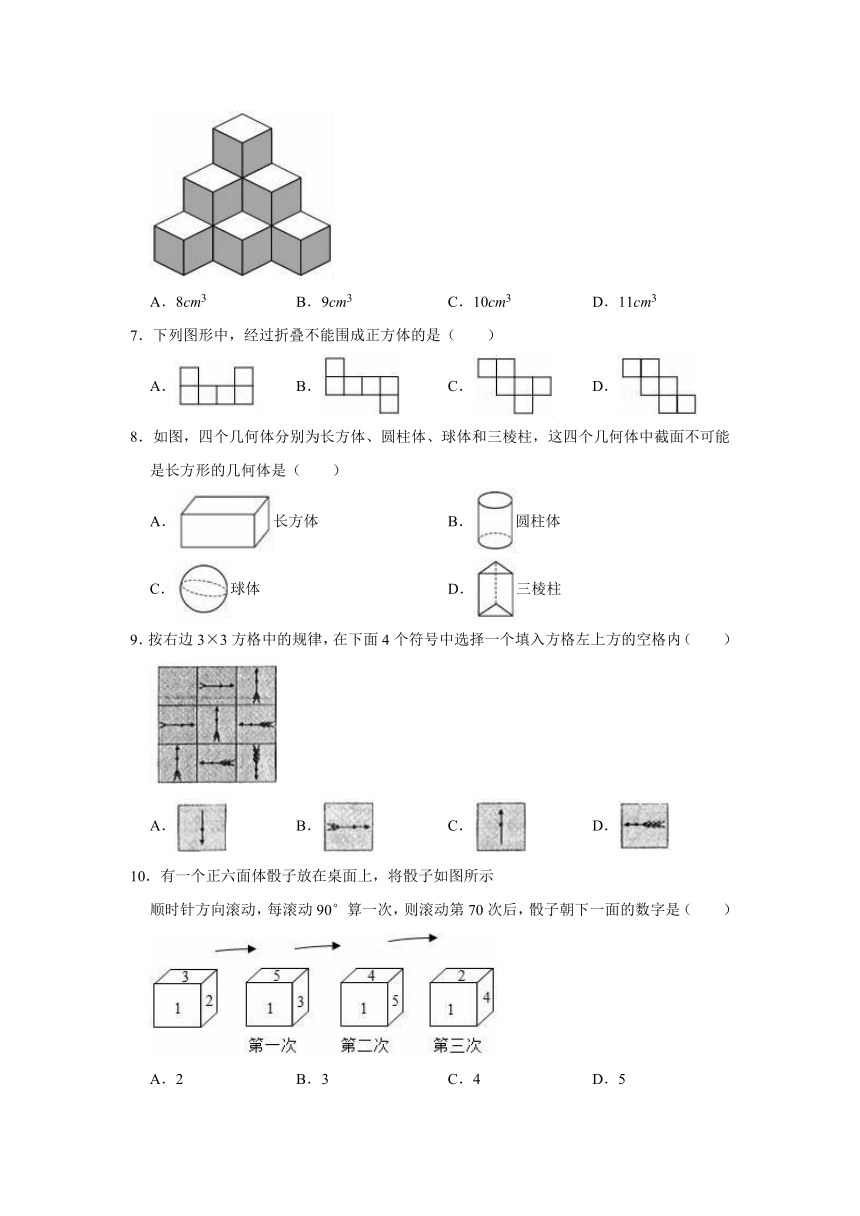
1.将下列图形绕着直线旋转一周正好得到如图所示的图形的是( )
A.
B.
C.
D.
2.求做一个圆柱形通风管要用多少铁皮,是求圆柱的( )
A.侧面积
B.底面积
C.表面积
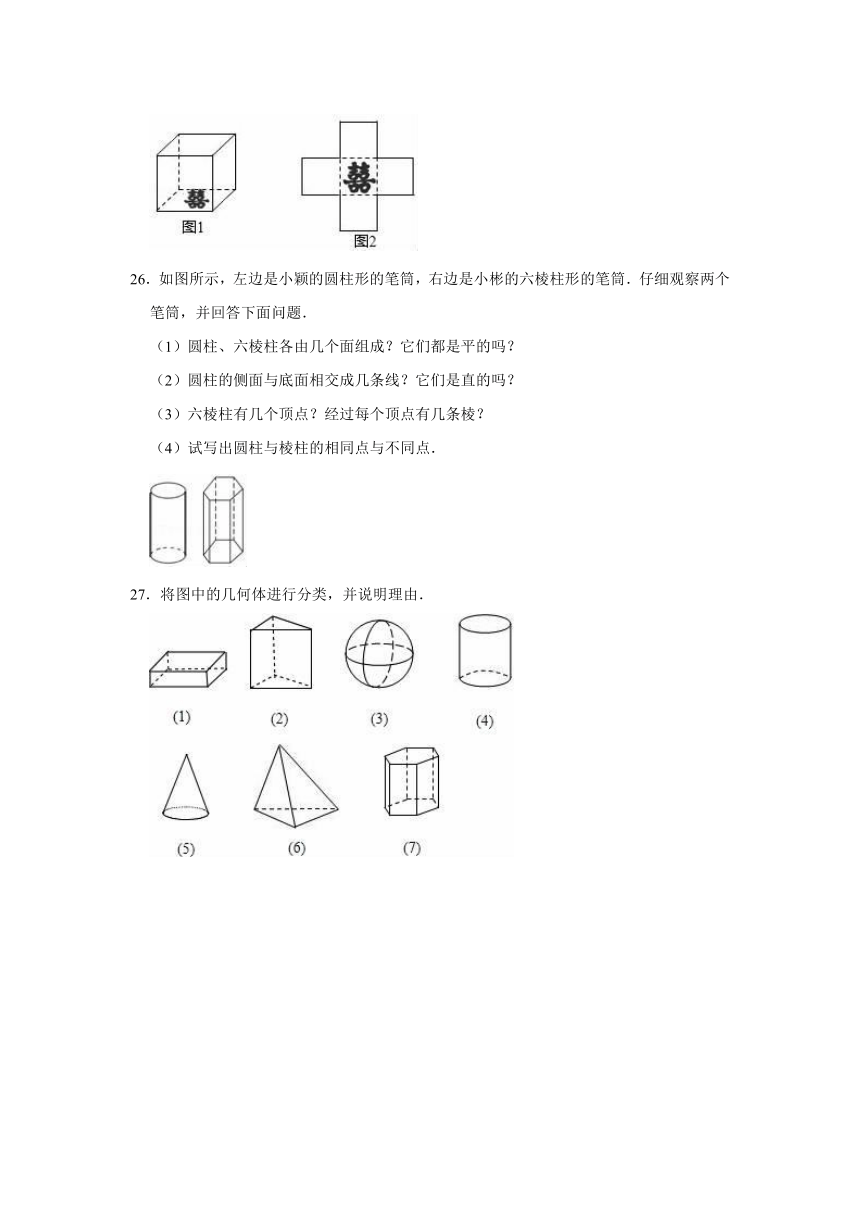
D.体积
3.下列图形可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
4.若一个棱柱有7个面,则它是( )
A.七棱柱
B.六棱柱
C.五棱柱
D.四棱柱
5.圆柱体的面数是( )
A.1
B.2
C.3
D.4
6.在墙角用若干个边长为1cm的小正方体摆成如图所示的几何体,则此几何体的体积为( )
A.8cm3
B.9cm3
C.10cm3
D.11cm3
7.下列图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
8.如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中截面不可能是长方形的几何体是( )
A.长方体
B.圆柱体
C.球体
D.三棱柱
9.按右边3×3方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )
A.
B.
C.
D.
10.有一个正六面体骰子放在桌面上,将骰子如图所示
顺时针方向滚动,每滚动90°算一次,则滚动第70次后,骰子朝下一面的数字是( )
A.2
B.3
C.4
D.5
二.填空题
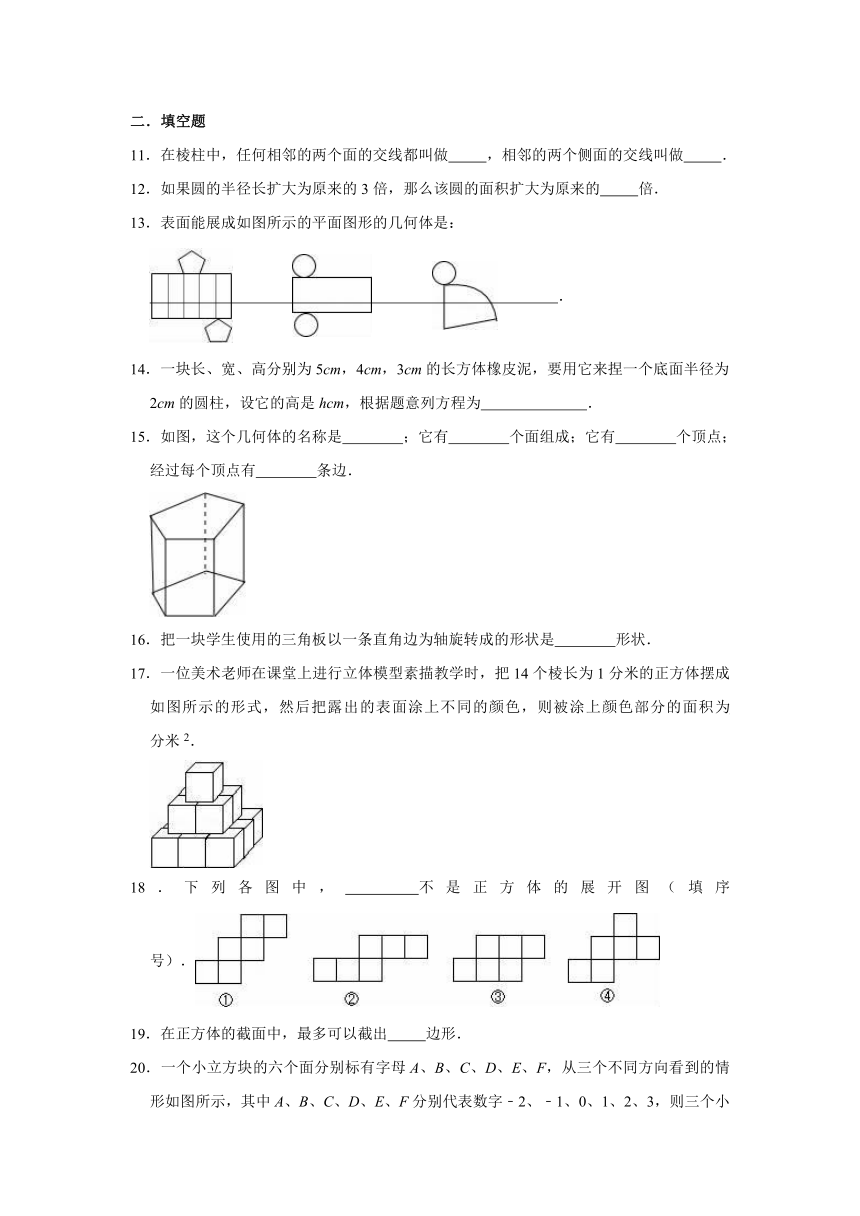
11.在棱柱中,任何相邻的两个面的交线都叫做
,相邻的两个侧面的交线叫做
.
12.如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的
倍.
13.表面能展成如图所示的平面图形的几何体是:
.
14.一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为
.
15.如图,这个几何体的名称是
;它有
个面组成;它有
个顶点;经过每个顶点有
条边.
16.把一块学生使用的三角板以一条直角边为轴旋转成的形状是
形状.
17.一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆成如图所示的形式,然后把露出的表面涂上不同的颜色,则被涂上颜色部分的面积为
分米2.
18.下列各图中,
不是正方体的展开图(填序号).
19.在正方体的截面中,最多可以截出
边形.
20.一个小立方块的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示,其中A、B、C、D、E、F分别代表数字﹣2、﹣1、0、1、2、3,则三个小立方块的下底面所标字母代表的数字的和为
.
三.解答题
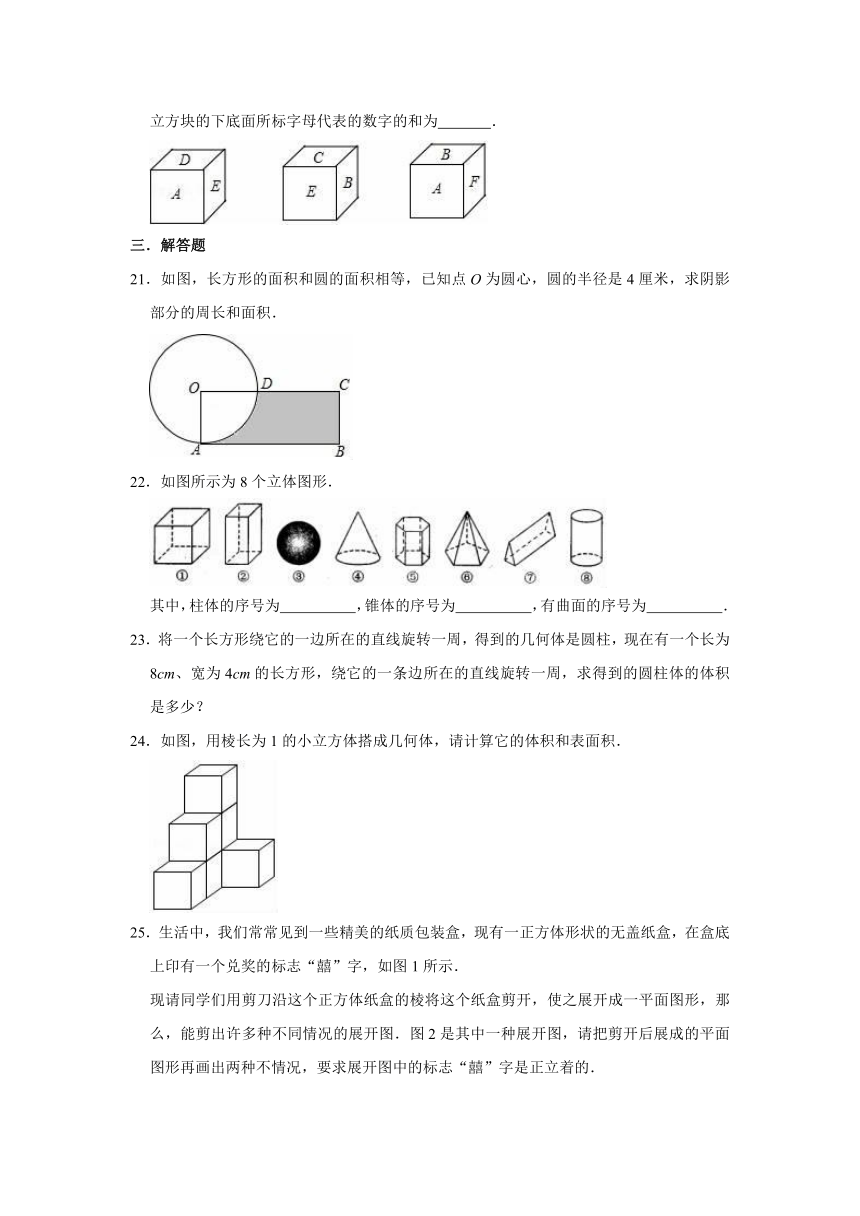
21.如图,长方形的面积和圆的面积相等,已知点O为圆心,圆的半径是4厘米,求阴影部分的周长和面积.
22.如图所示为8个立体图形.
其中,柱体的序号为
,锥体的序号为
,有曲面的序号为
.
23.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为8cm、宽为4cm的长方形,绕它的一条边所在的直线旋转一周,求得到的圆柱体的体积是多少?
24.如图,用棱长为1的小立方体搭成几何体,请计算它的体积和表面积.
25.生活中,我们常常见到一些精美的纸质包装盒,现有一正方体形状的无盖纸盒,在盒底上印有一个兑奖的标志“囍”字,如图1所示.
现请同学们用剪刀沿这个正方体纸盒的棱将这个纸盒剪开,使之展开成一平面图形,那么,能剪出许多种不同情况的展开图.图2是其中一种展开图,请把剪开后展成的平面图形再画出两种不情况,要求展开图中的标志“囍”字是正立着的.
26.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
27.将图中的几何体进行分类,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据选项中图形的特点,
A、可以通过旋转得到两个圆柱;故本选项正确;
B、可以通过旋转得到一个圆柱,一个圆筒;故本选项错误;
C、可以通过旋转得到一个圆柱,两个圆筒;故本选项错误;
D、可以通过旋转得到三个圆柱;故本选项错误.
故选:A.
2.解:做一个圆柱形的通风管需要的铁皮一定是面积,圆柱的表面积包括两个底面积和一个侧面积,题目当中要做的通风管无底无盖所以求的是侧面积.
故选:A.
3.解:A、不能作为一个正方体的展开图,故本选项错误;
B、不能作为一个正方体的展开图,故本选项错误;
C、能作为一个正方体的展开图,故本选项正确;
D、不能作为一个正方体的展开图,故本选项错误;
故选:C.
4.解:∵棱柱有七个面,
∴它有五个侧面,
∴它是五棱柱,
故选:C.
5.解:圆柱体是由两个圆形的底面,和一个弯曲的侧面围成的,
因此圆柱体是由三个面围成的,
故选:C.
6.解:图形中,小立方体的个数为1+3+6=10(块),
这个几何体的体积为1×1×1×10=10(cm3),
故选:C.
7.解:A、有两个面重叠,不能折成正方体;
选项B、C、D经过折叠均能围成正方体.
故选:A.
8.解:圆柱体、长方体、三棱柱的截面都可能出现长方形,只有球体的截面只与圆有关.
故选:C.
9.解:从下面的两排图形看出,应该是箭在依次作逆时针方向旋转,且每次逆时针方向旋转90度.
故选:A.
10.解:观察图形知道第一次点数五和点二数相对,第二次点数四和点数三相对,第三次点数二和点数五相对,第四次点数三和点数四相对,第五次点数五和点二数相对,且四次一循环,
∵70÷4=17…2,
∴滚动第70次后与第二次相同,
∴朝下的数字是4的对面3,
故选:B.
二.填空题
11.解:在棱柱中,任何相邻的两个面的交线都叫做棱,相邻的两个侧面的交线叫做侧棱.
故填:棱,侧棱.
12.解:设圆的半径为r,则它的面积为πr2,
如果圆的半径长扩大为原来的3倍,则半径为3r,则它的面积为π(3r)2=9πr2,
∴如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的9倍.
故答案为:9
13.解:经实际操作图形分别为:五棱柱,圆柱,圆锥.
14.解:根据等量关系列方程得:3×4×5=4πh,
故答案为:3×4×5=4πh.
15.解:这个几何体的名称是五棱柱;它有7个面组成;它有10个顶点;经过每个顶点有3条边.故答案为五棱柱、7、10、3.
16.解:把一块学生使用的三角板以一条直角边为轴旋转成的形状是圆锥体形状.
17.解:根据分析其表面积=4×(1+2+3)+9=33dm2,即涂上颜色的为33dm2.
故答案为33.
18.解:只要有“田”字格的展开图都不是正方体的表面展开图,所以③不是正方体的展开图.
故答案为:③.
19.解:用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此最多可以截出六边形.
故答案为:六.
20.解:由图形可知:A与B、D、E、F是邻面,故A和C为对面;
则B与A、C、E、F是邻面,故B和D为对面;
故E和F为对面;
则三个小立方块的下底面所标字母代表的数字的和为﹣1﹣2+1=﹣2.
故答案为:﹣2.
三.解答题
21.解:圆的面积:
3.14×42
=3.14×16
=50.24(平方厘米),
长方形的长:50.24÷4=12.56(厘米),
长方形的周长:(12.56+4)×2
=16.56×2
=33.12(厘米),
则阴影部分的周长:
33.12﹣4×2+3.14×4×2×=33.12﹣8+25.12×=25.12+6.28=31.4(厘米);
阴影部分的面积:
3.14×42×(1)
=3.14×16×=50.24×=37.68(平方厘米);
答:阴影部分的周长是31.4厘米,面积为37.68平方厘米.
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:①绕长所在的直线旋转一周得到圆柱体积为:π×42×8=128π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×82×4=256π(cm3).
答:得到的圆柱体的体积是分别是128πcm3或256πcm3.
24.解:小立方体的棱长是1,所以每个小立方体的体积是1,
有7个小立方体,所以这个几何体的体积是7;
从正面看,有4个面,从后面看有4个面,
从上面看,有4个面,从下面看,有4个面,
从左面看,有6个面,从右面看,有6个面,
所以几何体的表面积为(4+4+6)×2=28.
25.解:共能剪出8种不同情况的展开图,作图如下:
26.解:(1)圆柱有3个面,六棱柱有8个面,圆柱有两个平面,有一个曲面,棱柱的8个面都是平面;
(2)圆柱的侧面与底面相交形成1条线,是一条曲线;
(3)该棱柱共有12个顶点,经过每个顶点有3条棱;
(4)棱柱与圆柱的相同点是:都是柱体;
不同点是:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
27.解:分类首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.
(1)长方体是由平面组成的,属于柱体.
(2)三棱柱是由平面组成的,属于柱体.
(3)球体是由曲面组成的,属于球体.
(4)圆柱是由平面和曲面组成的,属于柱体.
(5)圆锥是由曲面与平面组成的,属于锥体.
(6)四棱锥是由平面组成的,属于锥体.
(7)六棱柱是由平面组成的,属于柱体.
若按组成几何体的面的平或曲来划分:(1)(2)(6)(7)是一类,组成它的各面全是平面;(3)(4)(5)是一类,组成它的面至少有一个是曲面,
若按柱、锥、球来划分:(1)(2)(4)(7)是一类,即柱体;(5)(6)是一类,即锥体;(3)是球体.
直线与角》单元测试卷
一.选择题
1.将下列图形绕着直线旋转一周正好得到如图所示的图形的是( )
A.
B.
C.
D.
2.求做一个圆柱形通风管要用多少铁皮,是求圆柱的( )
A.侧面积
B.底面积
C.表面积
D.体积
3.下列图形可以作为一个正方体的展开图的是( )
A.
B.
C.
D.
4.若一个棱柱有7个面,则它是( )
A.七棱柱
B.六棱柱
C.五棱柱
D.四棱柱
5.圆柱体的面数是( )
A.1
B.2
C.3
D.4
6.在墙角用若干个边长为1cm的小正方体摆成如图所示的几何体,则此几何体的体积为( )
A.8cm3
B.9cm3
C.10cm3
D.11cm3
7.下列图形中,经过折叠不能围成正方体的是( )
A.
B.
C.
D.
8.如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中截面不可能是长方形的几何体是( )
A.长方体
B.圆柱体
C.球体
D.三棱柱
9.按右边3×3方格中的规律,在下面4个符号中选择一个填入方格左上方的空格内( )
A.
B.
C.
D.
10.有一个正六面体骰子放在桌面上,将骰子如图所示
顺时针方向滚动,每滚动90°算一次,则滚动第70次后,骰子朝下一面的数字是( )
A.2
B.3
C.4
D.5
二.填空题
11.在棱柱中,任何相邻的两个面的交线都叫做
,相邻的两个侧面的交线叫做
.
12.如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的
倍.
13.表面能展成如图所示的平面图形的几何体是:
.
14.一块长、宽、高分别为5cm,4cm,3cm的长方体橡皮泥,要用它来捏一个底面半径为2cm的圆柱,设它的高是hcm,根据题意列方程为
.
15.如图,这个几何体的名称是
;它有
个面组成;它有
个顶点;经过每个顶点有
条边.
16.把一块学生使用的三角板以一条直角边为轴旋转成的形状是
形状.
17.一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体摆成如图所示的形式,然后把露出的表面涂上不同的颜色,则被涂上颜色部分的面积为
分米2.
18.下列各图中,
不是正方体的展开图(填序号).
19.在正方体的截面中,最多可以截出
边形.
20.一个小立方块的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示,其中A、B、C、D、E、F分别代表数字﹣2、﹣1、0、1、2、3,则三个小立方块的下底面所标字母代表的数字的和为
.
三.解答题
21.如图,长方形的面积和圆的面积相等,已知点O为圆心,圆的半径是4厘米,求阴影部分的周长和面积.
22.如图所示为8个立体图形.
其中,柱体的序号为
,锥体的序号为
,有曲面的序号为
.
23.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为8cm、宽为4cm的长方形,绕它的一条边所在的直线旋转一周,求得到的圆柱体的体积是多少?
24.如图,用棱长为1的小立方体搭成几何体,请计算它的体积和表面积.
25.生活中,我们常常见到一些精美的纸质包装盒,现有一正方体形状的无盖纸盒,在盒底上印有一个兑奖的标志“囍”字,如图1所示.
现请同学们用剪刀沿这个正方体纸盒的棱将这个纸盒剪开,使之展开成一平面图形,那么,能剪出许多种不同情况的展开图.图2是其中一种展开图,请把剪开后展成的平面图形再画出两种不情况,要求展开图中的标志“囍”字是正立着的.
26.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
27.将图中的几何体进行分类,并说明理由.
参考答案与试题解析
一.选择题
1.解:根据选项中图形的特点,
A、可以通过旋转得到两个圆柱;故本选项正确;
B、可以通过旋转得到一个圆柱,一个圆筒;故本选项错误;
C、可以通过旋转得到一个圆柱,两个圆筒;故本选项错误;
D、可以通过旋转得到三个圆柱;故本选项错误.
故选:A.
2.解:做一个圆柱形的通风管需要的铁皮一定是面积,圆柱的表面积包括两个底面积和一个侧面积,题目当中要做的通风管无底无盖所以求的是侧面积.
故选:A.
3.解:A、不能作为一个正方体的展开图,故本选项错误;
B、不能作为一个正方体的展开图,故本选项错误;
C、能作为一个正方体的展开图,故本选项正确;
D、不能作为一个正方体的展开图,故本选项错误;
故选:C.
4.解:∵棱柱有七个面,
∴它有五个侧面,
∴它是五棱柱,
故选:C.
5.解:圆柱体是由两个圆形的底面,和一个弯曲的侧面围成的,
因此圆柱体是由三个面围成的,
故选:C.
6.解:图形中,小立方体的个数为1+3+6=10(块),
这个几何体的体积为1×1×1×10=10(cm3),
故选:C.
7.解:A、有两个面重叠,不能折成正方体;
选项B、C、D经过折叠均能围成正方体.
故选:A.
8.解:圆柱体、长方体、三棱柱的截面都可能出现长方形,只有球体的截面只与圆有关.
故选:C.
9.解:从下面的两排图形看出,应该是箭在依次作逆时针方向旋转,且每次逆时针方向旋转90度.
故选:A.
10.解:观察图形知道第一次点数五和点二数相对,第二次点数四和点数三相对,第三次点数二和点数五相对,第四次点数三和点数四相对,第五次点数五和点二数相对,且四次一循环,
∵70÷4=17…2,
∴滚动第70次后与第二次相同,
∴朝下的数字是4的对面3,
故选:B.
二.填空题
11.解:在棱柱中,任何相邻的两个面的交线都叫做棱,相邻的两个侧面的交线叫做侧棱.
故填:棱,侧棱.
12.解:设圆的半径为r,则它的面积为πr2,
如果圆的半径长扩大为原来的3倍,则半径为3r,则它的面积为π(3r)2=9πr2,
∴如果圆的半径长扩大为原来的3倍,那么该圆的面积扩大为原来的9倍.
故答案为:9
13.解:经实际操作图形分别为:五棱柱,圆柱,圆锥.
14.解:根据等量关系列方程得:3×4×5=4πh,
故答案为:3×4×5=4πh.
15.解:这个几何体的名称是五棱柱;它有7个面组成;它有10个顶点;经过每个顶点有3条边.故答案为五棱柱、7、10、3.
16.解:把一块学生使用的三角板以一条直角边为轴旋转成的形状是圆锥体形状.
17.解:根据分析其表面积=4×(1+2+3)+9=33dm2,即涂上颜色的为33dm2.
故答案为33.
18.解:只要有“田”字格的展开图都不是正方体的表面展开图,所以③不是正方体的展开图.
故答案为:③.
19.解:用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此最多可以截出六边形.
故答案为:六.
20.解:由图形可知:A与B、D、E、F是邻面,故A和C为对面;
则B与A、C、E、F是邻面,故B和D为对面;
故E和F为对面;
则三个小立方块的下底面所标字母代表的数字的和为﹣1﹣2+1=﹣2.
故答案为:﹣2.
三.解答题
21.解:圆的面积:
3.14×42
=3.14×16
=50.24(平方厘米),
长方形的长:50.24÷4=12.56(厘米),
长方形的周长:(12.56+4)×2
=16.56×2
=33.12(厘米),
则阴影部分的周长:
33.12﹣4×2+3.14×4×2×=33.12﹣8+25.12×=25.12+6.28=31.4(厘米);
阴影部分的面积:
3.14×42×(1)
=3.14×16×=50.24×=37.68(平方厘米);
答:阴影部分的周长是31.4厘米,面积为37.68平方厘米.
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:①绕长所在的直线旋转一周得到圆柱体积为:π×42×8=128π(cm3);
②绕宽所在的直线旋转一周得到圆柱体积为:π×82×4=256π(cm3).
答:得到的圆柱体的体积是分别是128πcm3或256πcm3.
24.解:小立方体的棱长是1,所以每个小立方体的体积是1,
有7个小立方体,所以这个几何体的体积是7;
从正面看,有4个面,从后面看有4个面,
从上面看,有4个面,从下面看,有4个面,
从左面看,有6个面,从右面看,有6个面,
所以几何体的表面积为(4+4+6)×2=28.
25.解:共能剪出8种不同情况的展开图,作图如下:
26.解:(1)圆柱有3个面,六棱柱有8个面,圆柱有两个平面,有一个曲面,棱柱的8个面都是平面;
(2)圆柱的侧面与底面相交形成1条线,是一条曲线;
(3)该棱柱共有12个顶点,经过每个顶点有3条棱;
(4)棱柱与圆柱的相同点是:都是柱体;
不同点是:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
27.解:分类首先要确定标准,可以按组成几何体的面的平或曲来划分,也可以按柱、锥、球来划分.
(1)长方体是由平面组成的,属于柱体.
(2)三棱柱是由平面组成的,属于柱体.
(3)球体是由曲面组成的,属于球体.
(4)圆柱是由平面和曲面组成的,属于柱体.
(5)圆锥是由曲面与平面组成的,属于锥体.
(6)四棱锥是由平面组成的,属于锥体.
(7)六棱柱是由平面组成的,属于柱体.
若按组成几何体的面的平或曲来划分:(1)(2)(6)(7)是一类,组成它的各面全是平面;(3)(4)(5)是一类,组成它的面至少有一个是曲面,
若按柱、锥、球来划分:(1)(2)(4)(7)是一类,即柱体;(5)(6)是一类,即锥体;(3)是球体.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
