人教版八年级上册12.2三角形全等的判定练习题(word版含答案)
文档属性
| 名称 | 人教版八年级上册12.2三角形全等的判定练习题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 185.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 20:24:02 | ||
图片预览



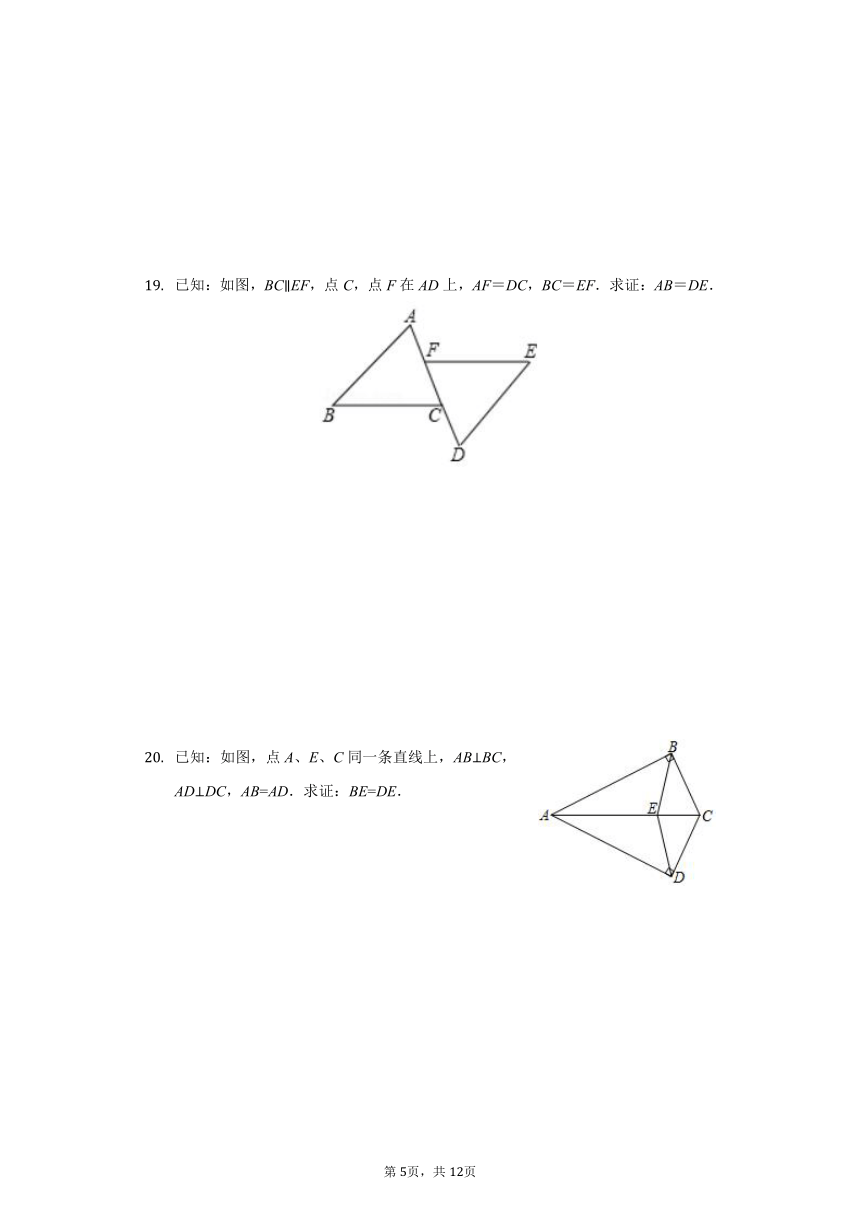
文档简介
12.2三角形全等的判定练习题(含答案)
一、选择题
如图,AC与BD相交于点P,AP=DP,则需要“SAS”证明△APB≌△DPC,还需添加的条件是( )
A.
B.
C.
D.
如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是( )
A.
SAS
B.
AAS
C.
SSS
D.
ASA
如图,AD
//
BC,AB
//
DC,则全等三角形共有()
???????
A.
2对
B.
3对
C.
4对
D.
5对
用直尺和圆规作一个角等于已知角的示意图如图,则说明∠A'O'B'=∠AOB,两个三角形全等的依据是( )
A.
SAS
B.
ASA
C.
SSS
D.
不能确定
如图,用“HL”判定Rt△ABC和Rt△DEF全等的条件可以是?
(???
)
A.
ACDF,BCEF
B.
AD,ABDE
C.
ACDF,ABDE
D.
BE,BCEF
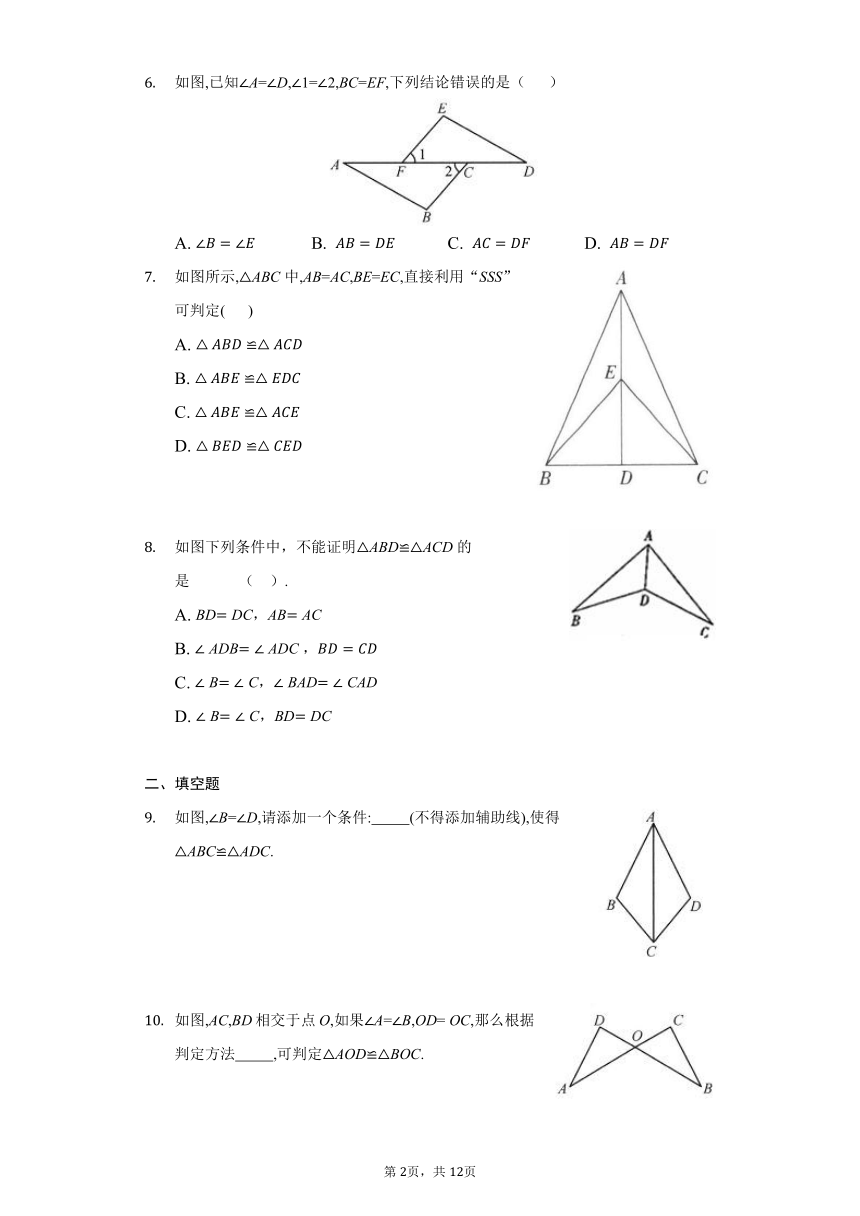
如图,已知A=D,1=2,BC=EF,下列结论错误的是(?
?
)???????
A.
B.
C.
D.
如图所示,ABC中,AB=AC,BE=EC,直接利用“SSS”可判定(?
?
)
A.
B.
C.
D.
如图下列条件中,不能证明△ABD≌△ACD的是?????????????(????).
A.
BD
DC,AB
AC
B.
ADB
ADC?,
C.
B
C,
BAD
CAD?
D.
B
C,BD
DC
二、填空题
如图,B=D,请添加一个条件:??????????(不得添加辅助线),使得ABCADC.
如图,AC,BD相交于点O,如果A=B,OD=
OC,那么根据判定方法??????????,可判定AODBOC.
如图,AB=ED,AC=CE,点C是BD的中点,若A=,则E=??????????.
如图,已知AE=BE,DE是AB的垂线,F为DE上一点,BF=11cm,CF=3cm,则AC=______.
如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连接BC并延长BC到点E,使CE=CB,连接DE,那么量出______
的长就等于AB的长.这是因为可根据______
方法判定△ABC≌△DEC.
两个锐角分别相等的直角三角形??????????全等.(填“一定”“不一定”或“一定不”)
如图,点D在线段BC上,DEAB于点E,DFBC交AC于点F,BD=CF,BE=CD.若AFD=,则EDF的度数为??????????.
在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于______.
三、解答题
如图,BA=BE,∠A=∠E,∠ABE=∠CBD,ED交BC于点F,且∠FBD=∠D.求证:AC∥BD.
证明:∵∠ABE=∠CBD(已知),
∴∠ABE+∠EBC=∠CBD+∠EBC(______),
即∠ABC=∠EBD,
在△ABC和△EBD中,,
∴△ABC≌△EBD(______),
∴∠C=∠D(______).
∵∠FBD=∠D,
∴∠C=______(______),
∴AC∥BD(______).
如图,D是△ABC的边AC上一点,点E在AC的延长线上,ED=AC,过点E作EF∥AB,并截取EF=AB,连接DF.求证:△EFD≌△ABC.
已知:如图,BC∥EF,点C,点F在AD上,AF=DC,BC=EF.求证:AB=DE.
已知:如图,点A、E、C同一条直线上,AB⊥BC,AD⊥DC,AB=AD.求证:BE=DE.
如图,在ABC中,AB=AC,BAC=,分别过点B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图,过点A的直线与斜边BC不相交时,
求证:ABECAF;EF=BE+CF.
?????????????
(2)如图,其他条件不变,过点A的直线与斜边BC相交时,若BE=10,CF=3,试求EF的长.
CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE__CF;(填“>”,“<”或“=”);EF,BE,AF三条线段的数量关系是:__________________.
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件___________,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并证明.
参考答案
1.B
2.A
3.C
4.C
5.C
6.D
7.C
8.D
9.(答案不唯一)BAC=DAC
10.AAS
11.???????
12.14cm
13.DE?
SAS
14.不一定
15.
16.20°
17.等式的性质?
ASA?
全等三角形对应角相等?
∠
FBD?
等量代换?
内错角相等,两直线平行
18.证明:∵EF∥AB,
∴∠E=∠A,
在△EFD和△ABC中,
,
∴△EFD≌△ABC(SAS).
19.证明:∵BC∥EF,
∴∠ACB=∠DFE,
∵AF=DC,
∴AC=DF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SAS),
∴AB=DE.
20.证明:∵AB⊥BC,AD⊥DC,
∴在Rt△ABC与Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAE=∠DAE,
在△ABE与△ADE中
,
∴△ABE≌△ADE(SAS),
∴BE=DE.
21.(1)证明:BEEF,CFEF,
AEB=CFA=.
EAB+EBA=.
BAC=,EAB+FAC=.
EBA=FAC.
在ABE和CAF中,
ABECAF(AAS).
由知ABECAF,
AE=CF,BE=AF.
EF=AF+AE=BE+CF.
(2)解:BEAF,CFAF,
AEB=CFA=.
EAB+EBA=.
BAC=,
EAB+FAC=.
EBA=FAC.
在ABE和CAF中,
ABECAF(AAS).
AE=CF,BE=AF.
EF=AF-AE=BE-CF=10-3=7.
22.(1)
①=,EF=|BE-AF|;
②∠α+∠ACB=180°.
?证明:如图2中,
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF-CE=BE-AF,
当E在F的右侧时,同理可证EF=AF-BE,
∴EF=|BE-AF|;
?(2)结论:EF=BE+AF.
理由:如图3中,
∵∠BEC=∠CFA=∠a,∠a=∠BCA,
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,
∴∠EBC+∠BCE=∠BCE+∠ACF,
∴∠EBC=∠ACF,
在△BEC和△CFA中,
,
∴△BEC≌△CFA(AAS),
∴AF=CE,BE=CF,
∵EF=CE+CF,
∴EF=BE+AF.
第2页,共2页
第1页,共1页
一、选择题
如图,AC与BD相交于点P,AP=DP,则需要“SAS”证明△APB≌△DPC,还需添加的条件是( )
A.
B.
C.
D.
如图,已知AB=DC,∠ABC=∠DCB,能直接判断△ABC≌△DCB的方法是( )
A.
SAS
B.
AAS
C.
SSS
D.
ASA
如图,AD
//
BC,AB
//
DC,则全等三角形共有()
???????
A.
2对
B.
3对
C.
4对
D.
5对
用直尺和圆规作一个角等于已知角的示意图如图,则说明∠A'O'B'=∠AOB,两个三角形全等的依据是( )
A.
SAS
B.
ASA
C.
SSS
D.
不能确定
如图,用“HL”判定Rt△ABC和Rt△DEF全等的条件可以是?
(???
)
A.
ACDF,BCEF
B.
AD,ABDE
C.
ACDF,ABDE
D.
BE,BCEF
如图,已知A=D,1=2,BC=EF,下列结论错误的是(?
?
)???????
A.
B.
C.
D.
如图所示,ABC中,AB=AC,BE=EC,直接利用“SSS”可判定(?
?
)
A.
B.
C.
D.
如图下列条件中,不能证明△ABD≌△ACD的是?????????????(????).
A.
BD
DC,AB
AC
B.
ADB
ADC?,
C.
B
C,
BAD
CAD?
D.
B
C,BD
DC
二、填空题
如图,B=D,请添加一个条件:??????????(不得添加辅助线),使得ABCADC.
如图,AC,BD相交于点O,如果A=B,OD=
OC,那么根据判定方法??????????,可判定AODBOC.
如图,AB=ED,AC=CE,点C是BD的中点,若A=,则E=??????????.
如图,已知AE=BE,DE是AB的垂线,F为DE上一点,BF=11cm,CF=3cm,则AC=______.
如图,有一池塘,要测池塘两端A,B两点的距离,可先在平地上取一个可以直接到达A,B两点的C,连接AC并延长AC到点D,使CD=CA,连接BC并延长BC到点E,使CE=CB,连接DE,那么量出______
的长就等于AB的长.这是因为可根据______
方法判定△ABC≌△DEC.
两个锐角分别相等的直角三角形??????????全等.(填“一定”“不一定”或“一定不”)
如图,点D在线段BC上,DEAB于点E,DFBC交AC于点F,BD=CF,BE=CD.若AFD=,则EDF的度数为??????????.
在△ABC中,已知∠CAB=60°,D、E分别是边AB、AC上的点,且∠AED=60°,ED+DB=CE,∠CDB=2∠CDE,则∠DCB等于______.
三、解答题
如图,BA=BE,∠A=∠E,∠ABE=∠CBD,ED交BC于点F,且∠FBD=∠D.求证:AC∥BD.
证明:∵∠ABE=∠CBD(已知),
∴∠ABE+∠EBC=∠CBD+∠EBC(______),
即∠ABC=∠EBD,
在△ABC和△EBD中,,
∴△ABC≌△EBD(______),
∴∠C=∠D(______).
∵∠FBD=∠D,
∴∠C=______(______),
∴AC∥BD(______).
如图,D是△ABC的边AC上一点,点E在AC的延长线上,ED=AC,过点E作EF∥AB,并截取EF=AB,连接DF.求证:△EFD≌△ABC.
已知:如图,BC∥EF,点C,点F在AD上,AF=DC,BC=EF.求证:AB=DE.
已知:如图,点A、E、C同一条直线上,AB⊥BC,AD⊥DC,AB=AD.求证:BE=DE.
如图,在ABC中,AB=AC,BAC=,分别过点B,C向过点A的直线作垂线,垂足分别为点E,F.
(1)如图,过点A的直线与斜边BC不相交时,
求证:ABECAF;EF=BE+CF.
?????????????
(2)如图,其他条件不变,过点A的直线与斜边BC相交时,若BE=10,CF=3,试求EF的长.
CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE__CF;(填“>”,“<”或“=”);EF,BE,AF三条线段的数量关系是:__________________.
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件___________,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想并证明.
参考答案
1.B
2.A
3.C
4.C
5.C
6.D
7.C
8.D
9.(答案不唯一)BAC=DAC
10.AAS
11.???????
12.14cm
13.DE?
SAS
14.不一定
15.
16.20°
17.等式的性质?
ASA?
全等三角形对应角相等?
∠
FBD?
等量代换?
内错角相等,两直线平行
18.证明:∵EF∥AB,
∴∠E=∠A,
在△EFD和△ABC中,
,
∴△EFD≌△ABC(SAS).
19.证明:∵BC∥EF,
∴∠ACB=∠DFE,
∵AF=DC,
∴AC=DF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SAS),
∴AB=DE.
20.证明:∵AB⊥BC,AD⊥DC,
∴在Rt△ABC与Rt△ADC中
,
∴Rt△ABC≌Rt△ADC(HL),
∴∠BAE=∠DAE,
在△ABE与△ADE中
,
∴△ABE≌△ADE(SAS),
∴BE=DE.
21.(1)证明:BEEF,CFEF,
AEB=CFA=.
EAB+EBA=.
BAC=,EAB+FAC=.
EBA=FAC.
在ABE和CAF中,
ABECAF(AAS).
由知ABECAF,
AE=CF,BE=AF.
EF=AF+AE=BE+CF.
(2)解:BEAF,CFAF,
AEB=CFA=.
EAB+EBA=.
BAC=,
EAB+FAC=.
EBA=FAC.
在ABE和CAF中,
ABECAF(AAS).
AE=CF,BE=AF.
EF=AF-AE=BE-CF=10-3=7.
22.(1)
①=,EF=|BE-AF|;
②∠α+∠ACB=180°.
?证明:如图2中,
∵∠BEC=∠CFA=∠a,∠α+∠ACB=180°,
∴∠CBE=∠ACF,
在△BCE和△CAF中,
,
∴△BCE≌△CAF(AAS),
∴BE=CF,CE=AF,
∴EF=CF-CE=BE-AF,
当E在F的右侧时,同理可证EF=AF-BE,
∴EF=|BE-AF|;
?(2)结论:EF=BE+AF.
理由:如图3中,
∵∠BEC=∠CFA=∠a,∠a=∠BCA,
又∵∠EBC+∠BCE+∠BEC=180°,∠BCE+∠ACF+∠ACB=180°,
∴∠EBC+∠BCE=∠BCE+∠ACF,
∴∠EBC=∠ACF,
在△BEC和△CFA中,
,
∴△BEC≌△CFA(AAS),
∴AF=CE,BE=CF,
∵EF=CE+CF,
∴EF=BE+AF.
第2页,共2页
第1页,共1页
