北京市101中学2011-2012学年七年级下学期期中考试数学试题
文档属性
| 名称 | 北京市101中学2011-2012学年七年级下学期期中考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 294.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-27 00:00:00 | ||
图片预览


文档简介
一、选择题:本大题共10小题,每题3分,共30分。(下列每小题中有四个备选答案,其中只有一个是符合题意的)
1. 以下各组数分别是三条线段的长度,其中可以构成三角形的是( )
A. 1,3,4 B. 1, 2,3 C. 6,6,10 D. 1,4,6
2. 点的坐标为(3,-4),则点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 如图,直线经过点,∥,,下列结论成立的是( )
A. B.
C. D.
4. 二元一次方程有无数多个解,下列四组值中不是该方程的解的是( )
A. B. C. D.
5. 如图,直线∥,,,则等于( )
A. 55° B. 60° C. 65° D. 70°
6. 如图,将正方形的一角折叠,折痕为,比大48°,设与∠BAD的度数分别为x和y,那么所适合的一个方程组是( )
A. B.
C. D.
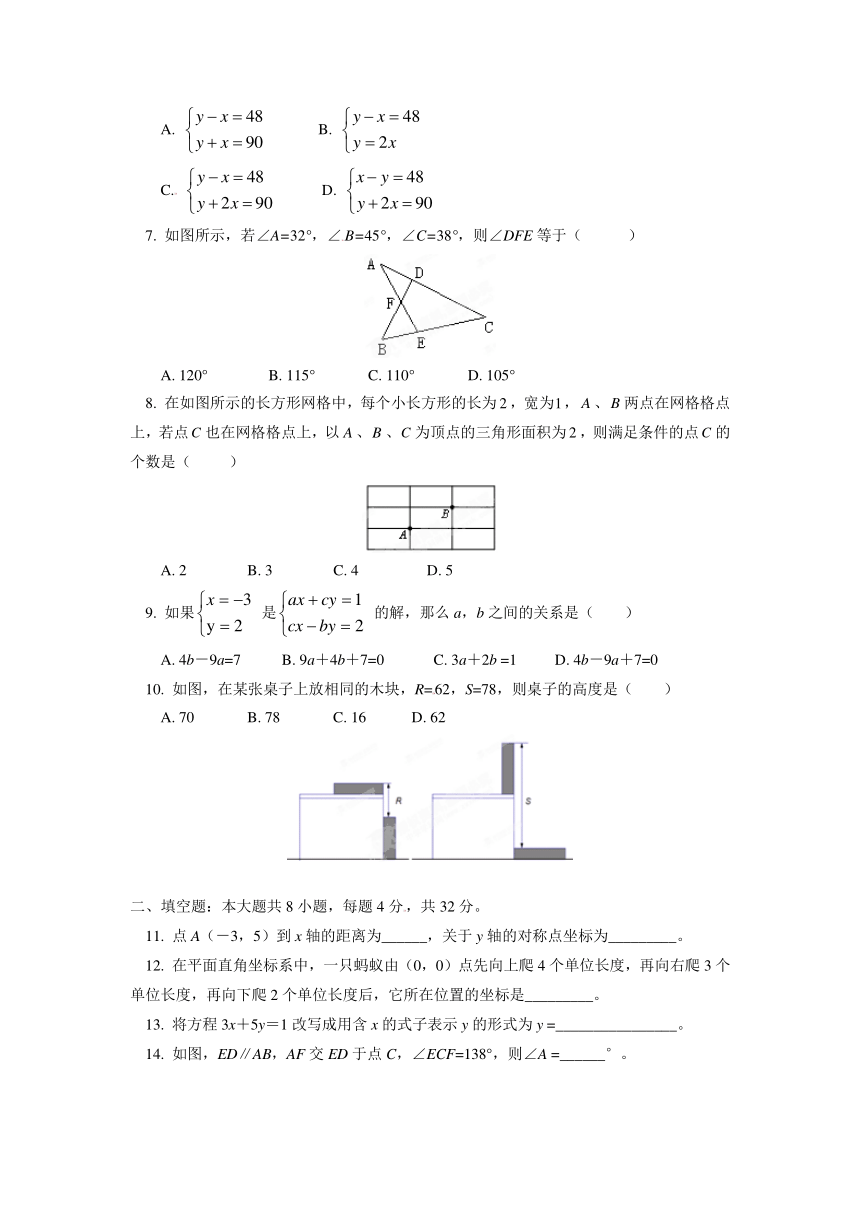
7. 如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A. 120° B. 115° C. 110° D. 105°
8. 在如图所示的长方形网格中,每个小长方形的长为,宽为,、两点在网格格点上,若点也在网格格点上,以、、为顶点的三角形面积为,则满足条件的点的个数是( )
A. 2 B. 3 C. 4 D. 5
9. 如果 是 的解,那么a,b之间的关系是( )
A. 4b-9a=7 B. 9a+4b+7=0 C. 3a+2b =1 D. 4b-9a+7=0
10. 如图,在某张桌子上放相同的木块,R=62,S=78,则桌子的高度是( )
A. 70 B. 78 C. 16 D. 62
二、填空题:本大题共8小题,每题4分,共32分。
11. 点A(-3,5)到x轴的距离为______,关于y轴的对称点坐标为_________。
12. 在平面直角坐标系中,一只蚂蚁由(0,0)点先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是_________。
13. 将方程3x+5y=1改写成用含x的式子表示y的形式为y =________________。
14. 如图,ED∥AB,AF交ED于点C,∠ECF=138°,则∠A =______°。
15. 已知等腰三角形的两条边长分别为4和7,则它的周长为 。
16. 如图,在长32米,宽20米的矩形草坪上建有两条等宽的弯曲小路,把草坪分成了4部分,若每条小路的宽度为2米,则草坪的面积为 平方米。
17. 给出下列程序,且已知当输入的x值为1时,输出值为1;输入的x值为-1时,输出值为-3,则当输入的x值为时,输出值为 。
18. 将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数。如数5对应的坐标为(-1,1),则数 对应的坐标是(-2,3),数2012对应的坐标是__________。
三、解答题:本大题共8小题,共58分。
19. (7分)如图所示,在△ABC中,
(1)画出BC边上的高AD和中线AE;
(2)若∠ACB=130°,求∠CAD的度数。
解:
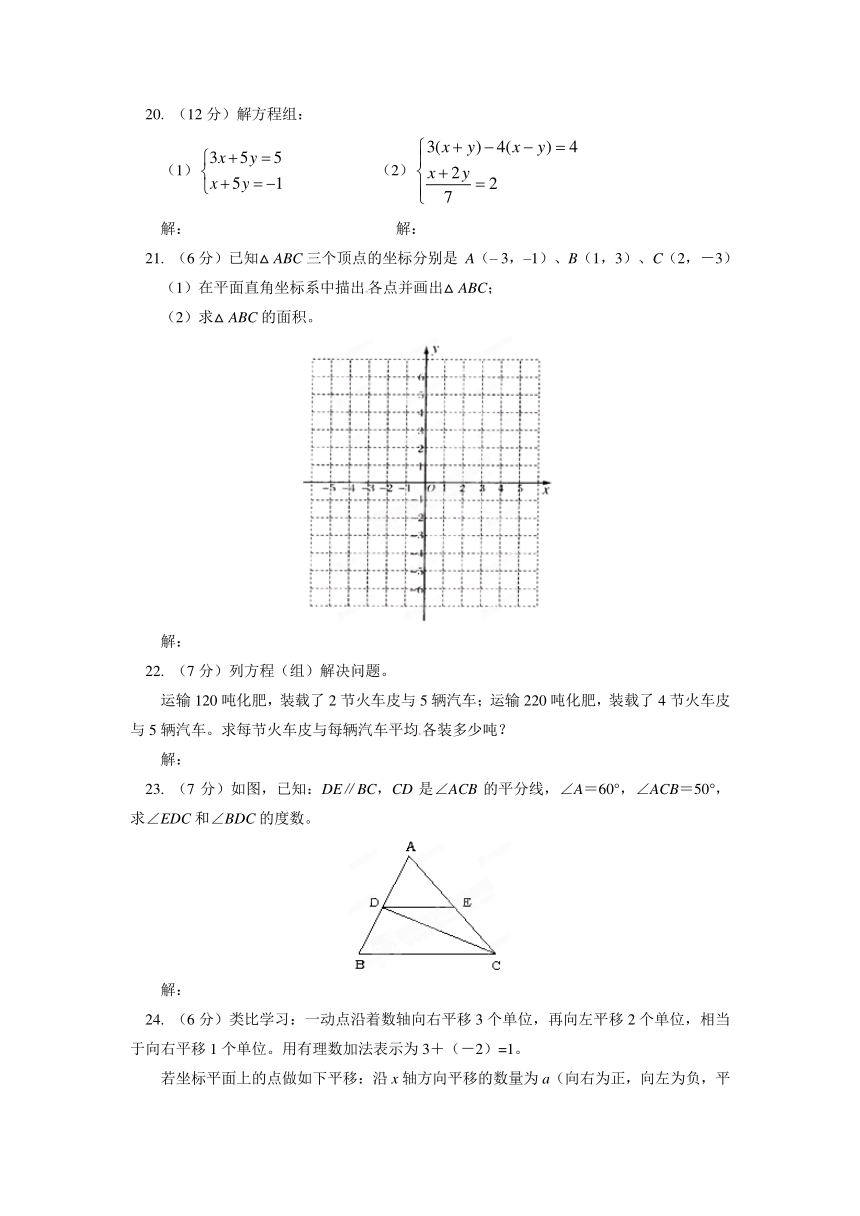
20. (12分)解方程组:
(1) (2)
解: 解:
21. (6分)已知△ABC三个顶点的坐标分别是 A(– 3,–1)、B(1,3)、C(2,-3)
(1)在平面直角坐标系中描出各点并画出△ABC;
(2)求△ABC的面积。
解:
22. (7分)列方程(组)解决问题。
运输120吨化肥,装载了2节火车皮与5辆汽车;运输220吨化肥,装载了4节火车皮与5辆汽车。求每节火车皮与每辆汽车平均各装多少吨?
解:
23. (7分)如图,已知:DE∥BC,CD是∠ACB的平分线,∠A=60°,∠ACB=50°,求∠EDC和∠BDC的度数。
解:
24. (6分)类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位。用有理数加法表示为3+(-2)=1。
若坐标平面上的点做如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为。
解决问题:
(1)计算:{3,1}+{1,-2};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照 “平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC。
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程。
解:(1){3,1}+{1,-2}= ;
(2)答: ;
(3)加法算式: 。
25. (6分)如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,
求∠DAC的度数。
解:
26. (7分)点P是△ABD中AD边上一点,
(1)如图1,当P为AD中点时,则有S△ABP= S△ABD;
(2)如图2,在四边形ABCD中,P是AD边上任意一点,△PBC的面积为,△ABC的面积为,△DBC的面积为。
①当AP=AD时,如图3,试探究、、之间的关系?写出求解过程;
②一般地,当AP=AD(n表示正整数)时,试探究、、之间的关系?写出求解过程。
解:
【试题答案】
一、选择题:本大题共10小题,每题3分,共30分。
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B C C B C B A
二、填空题:本大题共10小题,共30分。
三、解答题:本大题共8小题,共58分。
19. (1)略
(2)40°
21. (1)略
(2)△ABC的面积为14。
22. 解:设每节火车皮装x吨化肥,每辆汽车装y吨化肥
由题意得
解得
25.
26. (1)S△ABP=S△ABD;
(2)①当AP=AD时(如图②):
∵AP=AD,△ABP和△ABD的高相等,
∴S△ABP=S△ABD。
=S△DBC+S△ABC。
②S△PBC=S△DBC+S△ABC;
∵AP=AD,△ABP和△ABD的高相等,
∴S△ABP=S△ABD。
又∵PD=AD-AP=AD,△CDP和△CDA的高相等,
∴S△CDP=S△CDA
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-S△ABD-S△CDA
=S四边形ABCD-(S四边形ABCD-S△DBC)-(S四边形ABCD-S△ABC)
=S△DBC+S△ABC。
∴S△PBC=S△DBC+S△ABC
x
1. 以下各组数分别是三条线段的长度,其中可以构成三角形的是( )
A. 1,3,4 B. 1, 2,3 C. 6,6,10 D. 1,4,6
2. 点的坐标为(3,-4),则点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 如图,直线经过点,∥,,下列结论成立的是( )
A. B.
C. D.
4. 二元一次方程有无数多个解,下列四组值中不是该方程的解的是( )
A. B. C. D.
5. 如图,直线∥,,,则等于( )
A. 55° B. 60° C. 65° D. 70°
6. 如图,将正方形的一角折叠,折痕为,比大48°,设与∠BAD的度数分别为x和y,那么所适合的一个方程组是( )
A. B.
C. D.
7. 如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A. 120° B. 115° C. 110° D. 105°
8. 在如图所示的长方形网格中,每个小长方形的长为,宽为,、两点在网格格点上,若点也在网格格点上,以、、为顶点的三角形面积为,则满足条件的点的个数是( )
A. 2 B. 3 C. 4 D. 5
9. 如果 是 的解,那么a,b之间的关系是( )
A. 4b-9a=7 B. 9a+4b+7=0 C. 3a+2b =1 D. 4b-9a+7=0
10. 如图,在某张桌子上放相同的木块,R=62,S=78,则桌子的高度是( )
A. 70 B. 78 C. 16 D. 62
二、填空题:本大题共8小题,每题4分,共32分。
11. 点A(-3,5)到x轴的距离为______,关于y轴的对称点坐标为_________。
12. 在平面直角坐标系中,一只蚂蚁由(0,0)点先向上爬4个单位长度,再向右爬3个单位长度,再向下爬2个单位长度后,它所在位置的坐标是_________。
13. 将方程3x+5y=1改写成用含x的式子表示y的形式为y =________________。
14. 如图,ED∥AB,AF交ED于点C,∠ECF=138°,则∠A =______°。
15. 已知等腰三角形的两条边长分别为4和7,则它的周长为 。
16. 如图,在长32米,宽20米的矩形草坪上建有两条等宽的弯曲小路,把草坪分成了4部分,若每条小路的宽度为2米,则草坪的面积为 平方米。
17. 给出下列程序,且已知当输入的x值为1时,输出值为1;输入的x值为-1时,输出值为-3,则当输入的x值为时,输出值为 。
18. 将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数。如数5对应的坐标为(-1,1),则数 对应的坐标是(-2,3),数2012对应的坐标是__________。
三、解答题:本大题共8小题,共58分。
19. (7分)如图所示,在△ABC中,
(1)画出BC边上的高AD和中线AE;
(2)若∠ACB=130°,求∠CAD的度数。
解:
20. (12分)解方程组:
(1) (2)
解: 解:
21. (6分)已知△ABC三个顶点的坐标分别是 A(– 3,–1)、B(1,3)、C(2,-3)
(1)在平面直角坐标系中描出各点并画出△ABC;
(2)求△ABC的面积。
解:
22. (7分)列方程(组)解决问题。
运输120吨化肥,装载了2节火车皮与5辆汽车;运输220吨化肥,装载了4节火车皮与5辆汽车。求每节火车皮与每辆汽车平均各装多少吨?
解:
23. (7分)如图,已知:DE∥BC,CD是∠ACB的平分线,∠A=60°,∠ACB=50°,求∠EDC和∠BDC的度数。
解:
24. (6分)类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位。用有理数加法表示为3+(-2)=1。
若坐标平面上的点做如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为。
解决问题:
(1)计算:{3,1}+{1,-2};
(2)动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量”
{1,2}平移到B;若先把动点P按照 “平移量”{1,2}平移到C,再按照“平移量”
{3,1}平移,最后的位置还是点B吗 在图1中画出四边形OABC。
(3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O. 请用“平移量”加法算式表示它的航行过程。
解:(1){3,1}+{1,-2}= ;
(2)答: ;
(3)加法算式: 。
25. (6分)如图所示,在△ABC中,D是BC边上一点,∠1=∠2,∠3=∠4,∠BAC=63°,
求∠DAC的度数。
解:
26. (7分)点P是△ABD中AD边上一点,
(1)如图1,当P为AD中点时,则有S△ABP= S△ABD;
(2)如图2,在四边形ABCD中,P是AD边上任意一点,△PBC的面积为,△ABC的面积为,△DBC的面积为。
①当AP=AD时,如图3,试探究、、之间的关系?写出求解过程;
②一般地,当AP=AD(n表示正整数)时,试探究、、之间的关系?写出求解过程。
解:
【试题答案】
一、选择题:本大题共10小题,每题3分,共30分。
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B B C C B C B A
二、填空题:本大题共10小题,共30分。
三、解答题:本大题共8小题,共58分。
19. (1)略
(2)40°
21. (1)略
(2)△ABC的面积为14。
22. 解:设每节火车皮装x吨化肥,每辆汽车装y吨化肥
由题意得
解得
25.
26. (1)S△ABP=S△ABD;
(2)①当AP=AD时(如图②):
∵AP=AD,△ABP和△ABD的高相等,
∴S△ABP=S△ABD。
=S△DBC+S△ABC。
②S△PBC=S△DBC+S△ABC;
∵AP=AD,△ABP和△ABD的高相等,
∴S△ABP=S△ABD。
又∵PD=AD-AP=AD,△CDP和△CDA的高相等,
∴S△CDP=S△CDA
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD-S△ABD-S△CDA
=S四边形ABCD-(S四边形ABCD-S△DBC)-(S四边形ABCD-S△ABC)
=S△DBC+S△ABC。
∴S△PBC=S△DBC+S△ABC
x
同课章节目录
