九年级数学圆心角与圆周角的关系
文档属性
| 名称 | 九年级数学圆心角与圆周角的关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 87.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-27 00:00:00 | ||
图片预览



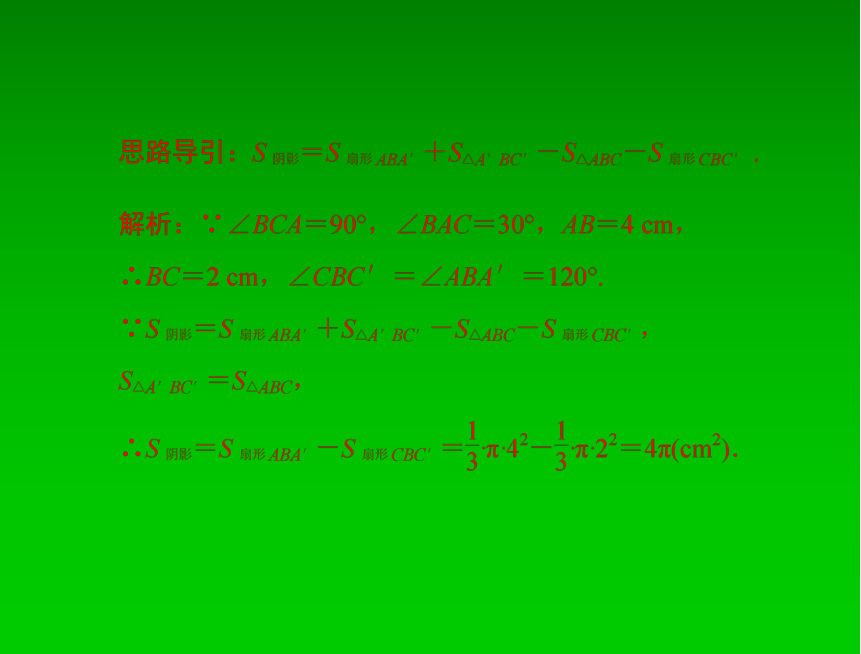
文档简介
(共14张PPT)
章末热点考向专题
专题一
圆心角与圆周角的关系
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于
该弧所对的圆心角的一半,相等的圆周角所对的弧相等.半圆
(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
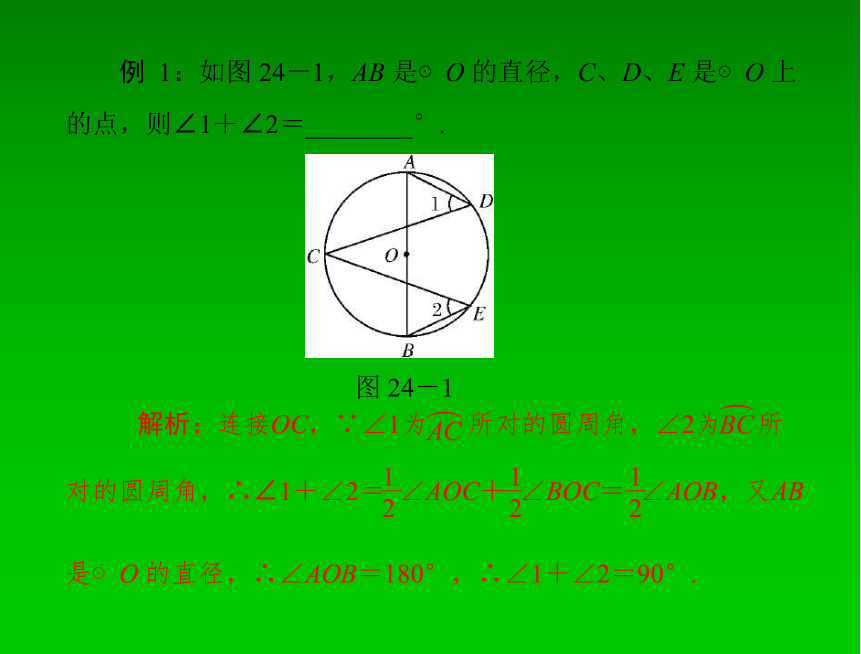
例 1:如图 24-1,AB 是⊙O 的直径,C、D、E 是⊙O 上
的点,则∠1+∠2=________°.
图 24-1
解析:连接OC,∵∠1为 所对的圆周角,∠2为 所
对的圆周角,∴∠1+∠2= ∠AOC+ ∠BOC= ∠AOB,又AB
1 1 1
2 2 2
是⊙O 的直径,∴∠AOB=180°,∴∠1+∠2=90°.
专题二
圆与圆的位置关系
圆与圆的位置关系中,时常要注意两圆相切包括外切和内
切两种情况.
例2:已知△ABC 的三边分别是 a、b、c,两圆的半径 r1
=a,r2=b,圆心距 d=c,则这两个圆的位置关系是__________.
解析:∵△ABC 的三边分别是a、b、c,∴a+b>c,即r1
+r2>d,∴两圆相交.
专题三
求与圆有关的阴影部分的面积
求圆中不规则阴影图形的面积,通常用割补法,将其面积
用规则图形(如扇形、三角形、矩形等)的面积的和或差表示.
例 3:如图 24-2,将△ABC 绕点 B 逆时针旋转到A′BC′
使 A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,
AB=4 cm,则图中阴影部分面积为__________cm2.
图 24-2
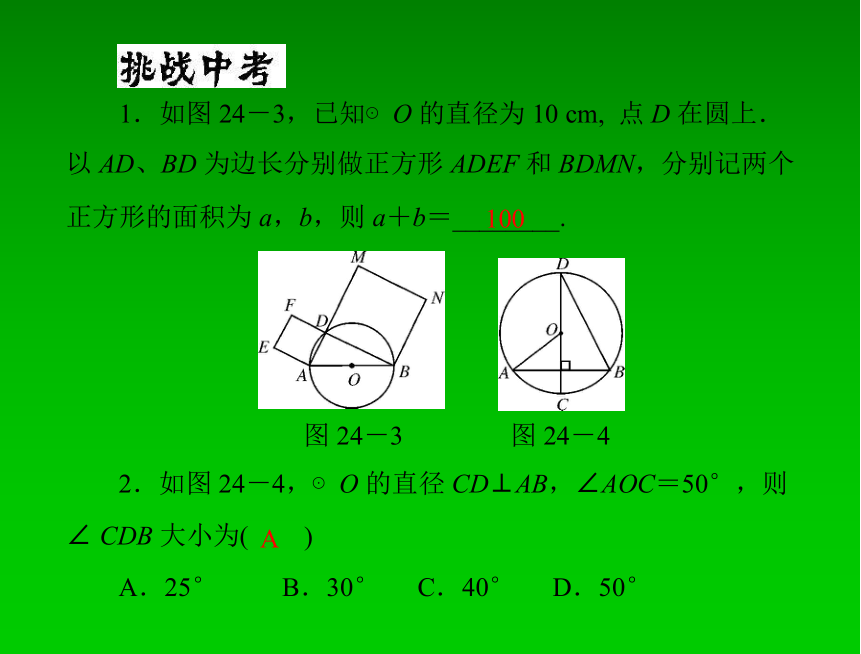
1.如图 24-3,已知⊙O 的直径为 10 cm, 点 D 在圆上.
以 AD、BD 为边长分别做正方形 ADEF 和 BDMN,分别记两个
正方形的面积为 a,b,则 a+b=________.
100
图 24-3
图 24-4
2.如图 24-4,⊙O 的直径 CD⊥AB,∠AOC=50°,则
∠ CDB 大小为(
)
A
A.25°
B.30°
C.40°
D.50°
3.若⊙O1 与⊙O2 至多有一个交点,且 O1O2=5,⊙O1 的
半径 r1=2,则⊙O2 的半径 r2 的取值范围是(
)
D
A.3≤r≤7
C.07
B.3D.04.如图 24-5,⊙O1、⊙O2 的直径分别为 2 cm 和 4 cm,
现将⊙O1 向⊙O2 平移,当 O1O2=__________cm 时,⊙O1与⊙
O2 相切.
1 或 3
图 24-5
5.(2010 年广东湛江)已知两圆的半径分别为 3 cm 和 4 cm,
两个圆的圆心距为 8 cm,则两圆的位置关系是(
)
C
A.内切
B.相交
C.外离
D.外切
6.(2010 年广东珠海)如图 24-6, PA 、PB 是⊙O 的切线,
)
C
切点分别是 A、B,如果∠P=60°,那么∠AOB 等于(
图 24-6
A.60°
B.90°
C.120°
D.150°
7.(2010 年广东深圳)如图 24-7,点 P(3a,a)是反比例函
则反比例函数的解析式为(
D
)
图 24-7
A.y=
3
x
B.y=
5
x
C.y=
10
x
D.y=
12
x
8.(2010 年广东)如图 24-8,PA 与⊙O 相切于点 A,弦 AB
⊥OP,垂足为 C,OP 与⊙O 相交于 D 点,已知 OA=2,OP=4.
(1)求∠POA 的度数;
(2)计算弦 AB 的长.
图 24-8
解:(1)60°
(2)AB=
9.(1)如图 24-9(1),已知△ABC 是边长为 2 的等边三角形,
以 BC 为直径的⊙O 交 AB、AC 于 D、E.求证:△ADE 是等边三
角形;
(2)在(1)的条件下,若一个圆锥的侧面展开图是扇形 ODE,
求这个圆锥的全面积;
(3)如图 24-9(2),若∠A=60°,AB≠AC,则(1)的结论是否
成立?如果成立,请给出证明;如果不成立,请说明理由.
图 24-9
(1)证明:易知∠ADE+∠BDE=180°,
又由圆周角的知识知道∠C+∠BDE=180°,故∠ADE=∠C.
又∵△ABC 是等边三角形,∴∠ADE=∠C=60°.
∴△ADE 是等边三角形.
(2)解:易知∠B=60°,
又∵DO=BO,∴△BDO 是等边三角形,∴∠DOB=60°.
同理,∠EOC=60°.即∠DOE=60°.
∵等边△ABC 边长为 2,∴DO=OE=1.
(3)解:不成立.理由:由(1)知道,若△ADE 是等边三角形,
则∠ADE=∠C=60°.又∠A=60°,故△ABC 是等边三角形,即
AB=AC,与题设矛盾.
章末热点考向专题
专题一
圆心角与圆周角的关系
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于
该弧所对的圆心角的一半,相等的圆周角所对的弧相等.半圆
(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
例 1:如图 24-1,AB 是⊙O 的直径,C、D、E 是⊙O 上
的点,则∠1+∠2=________°.
图 24-1
解析:连接OC,∵∠1为 所对的圆周角,∠2为 所
对的圆周角,∴∠1+∠2= ∠AOC+ ∠BOC= ∠AOB,又AB
1 1 1
2 2 2
是⊙O 的直径,∴∠AOB=180°,∴∠1+∠2=90°.
专题二
圆与圆的位置关系
圆与圆的位置关系中,时常要注意两圆相切包括外切和内
切两种情况.
例2:已知△ABC 的三边分别是 a、b、c,两圆的半径 r1
=a,r2=b,圆心距 d=c,则这两个圆的位置关系是__________.
解析:∵△ABC 的三边分别是a、b、c,∴a+b>c,即r1
+r2>d,∴两圆相交.
专题三
求与圆有关的阴影部分的面积
求圆中不规则阴影图形的面积,通常用割补法,将其面积
用规则图形(如扇形、三角形、矩形等)的面积的和或差表示.
例 3:如图 24-2,将△ABC 绕点 B 逆时针旋转到A′BC′
使 A、B、C′在同一直线上,若∠BCA=90°,∠BAC=30°,
AB=4 cm,则图中阴影部分面积为__________cm2.
图 24-2
1.如图 24-3,已知⊙O 的直径为 10 cm, 点 D 在圆上.
以 AD、BD 为边长分别做正方形 ADEF 和 BDMN,分别记两个
正方形的面积为 a,b,则 a+b=________.
100
图 24-3
图 24-4
2.如图 24-4,⊙O 的直径 CD⊥AB,∠AOC=50°,则
∠ CDB 大小为(
)
A
A.25°
B.30°
C.40°
D.50°
3.若⊙O1 与⊙O2 至多有一个交点,且 O1O2=5,⊙O1 的
半径 r1=2,则⊙O2 的半径 r2 的取值范围是(
)
D
A.3≤r≤7
C.0
B.3
现将⊙O1 向⊙O2 平移,当 O1O2=__________cm 时,⊙O1与⊙
O2 相切.
1 或 3
图 24-5
5.(2010 年广东湛江)已知两圆的半径分别为 3 cm 和 4 cm,
两个圆的圆心距为 8 cm,则两圆的位置关系是(
)
C
A.内切
B.相交
C.外离
D.外切
6.(2010 年广东珠海)如图 24-6, PA 、PB 是⊙O 的切线,
)
C
切点分别是 A、B,如果∠P=60°,那么∠AOB 等于(
图 24-6
A.60°
B.90°
C.120°
D.150°
7.(2010 年广东深圳)如图 24-7,点 P(3a,a)是反比例函
则反比例函数的解析式为(
D
)
图 24-7
A.y=
3
x
B.y=
5
x
C.y=
10
x
D.y=
12
x
8.(2010 年广东)如图 24-8,PA 与⊙O 相切于点 A,弦 AB
⊥OP,垂足为 C,OP 与⊙O 相交于 D 点,已知 OA=2,OP=4.
(1)求∠POA 的度数;
(2)计算弦 AB 的长.
图 24-8
解:(1)60°
(2)AB=
9.(1)如图 24-9(1),已知△ABC 是边长为 2 的等边三角形,
以 BC 为直径的⊙O 交 AB、AC 于 D、E.求证:△ADE 是等边三
角形;
(2)在(1)的条件下,若一个圆锥的侧面展开图是扇形 ODE,
求这个圆锥的全面积;
(3)如图 24-9(2),若∠A=60°,AB≠AC,则(1)的结论是否
成立?如果成立,请给出证明;如果不成立,请说明理由.
图 24-9
(1)证明:易知∠ADE+∠BDE=180°,
又由圆周角的知识知道∠C+∠BDE=180°,故∠ADE=∠C.
又∵△ABC 是等边三角形,∴∠ADE=∠C=60°.
∴△ADE 是等边三角形.
(2)解:易知∠B=60°,
又∵DO=BO,∴△BDO 是等边三角形,∴∠DOB=60°.
同理,∠EOC=60°.即∠DOE=60°.
∵等边△ABC 边长为 2,∴DO=OE=1.
(3)解:不成立.理由:由(1)知道,若△ADE 是等边三角形,
则∠ADE=∠C=60°.又∠A=60°,故△ABC 是等边三角形,即
AB=AC,与题设矛盾.
同课章节目录
