冀教版数学九年级上册28.5弧长和扇形面积 课件(共17张PPT)
文档属性
| 名称 | 冀教版数学九年级上册28.5弧长和扇形面积 课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 816.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 20:41:44 | ||
图片预览





文档简介
(共17张PPT)
28.5
弧长和扇形面积
第二十八章
圆
导入新课
讲授新课
当堂练习
课堂小结
1.理解并掌握扇形的弧长的计算公式并会进行计算.
2.理解并掌握扇形的面积的计算公式并会进行计算.
(重点)
3.能够根据圆锥侧面展开图进行相关计算.(难点)
学习目标
问题1
已知⊙O半径为R,⊙O的周长C是多少?
导入新课
回顾与思考
C=2πR
问题2
已知⊙O半径为R,⊙O的面积S是多少?
S=πR2
讲授新课
扇形的弧长
一
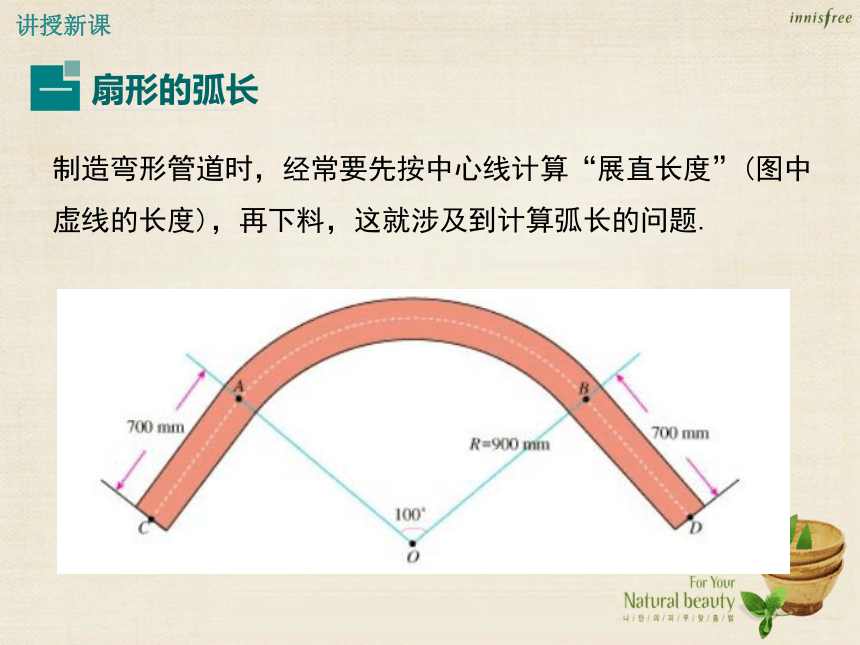
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料,这就涉及到计算弧长的问题.
已知⊙O半径为R,求n°圆心角所对弧长.
(1)半径为R的圆,周长是多少?
C=2πR
(2)1°圆心角所对弧长是多少?
(3)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
(4)n°圆心角所对弧长是多少?
l
A
B
O
n°
)
.
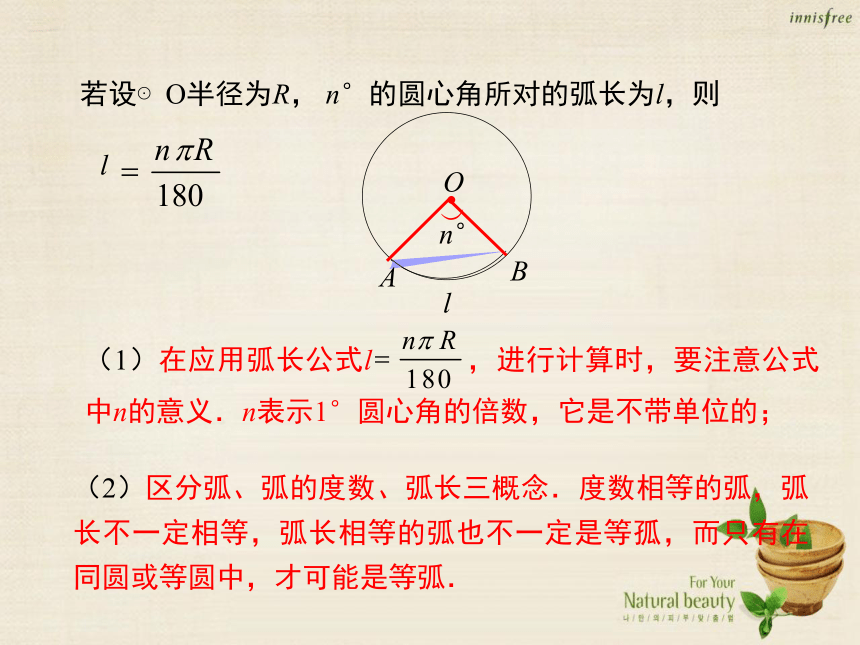
若设⊙O半径为R,
n°的圆心角所对的弧长为l,则
l
(1)在应用弧长公式l
,进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
l
A
B
O
n°
)
.
扇形的面积
二
已知⊙O半径为R,如何求圆心角n°的扇形的面积?
研究问题的步骤:
(1)半径为R的圆,面积是多少?
S=πR2
(2)圆心角为1°的扇形的面积是多少?
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少?
扇形面积公式:
若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,
则S扇形=
.
注意:
(1)在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆).
问题:扇形的面积公式与弧长公式有联系吗?
想一想:扇形的面积公式与什么公式类似?
如果扇形的半径为R的圆中,圆心角为no
,那么扇形面积的计算公式为:
扇形面积的弧长与扇形面积:
合作探究
圆锥侧面展开图的相关计算
三
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点和底面圆上任一点的线段叫做圆锥的母线.
连接顶点与底面圆的圆心O的线段叫做圆锥的高.
思考圆锥的母线和圆锥的高有哪些性质?
h
l
r
由勾股定理得:
如果用r表示圆锥底面的半径,
h表示圆锥的高线长,l表示圆锥的母线长,那么r,h,l之间有怎样的数量关系呢?
r2
+
h
2
=
l
2
A
B
O
C
圆锥的侧面展开图是扇形
A
B
O
C
其侧面展开图扇形的半径=母线的长l
l
S
A
O
B
r
侧面展开图扇形的弧长=底面周长
请推导出圆锥的侧面积公式.
S
侧
=πrl
(r表示圆锥底面的半径,
l
表示圆锥的母线长
)
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
l
r
当堂练习
1.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
答:管道的展直长度为2970mm.
2.圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求这个烟囱帽的面积(
取3.14,结果保留2个有效数字).
解:∵l=80,h=38.7
∴r=
∴S侧=πrl≈3.14×70×80≈1.8×104(cm2)
答:烟囱帽的面积约为1.8×104cm2.
l
h
r
课堂小结
1.n°的圆心角所对的弧长
.
2.圆心角为n°的扇形面积S扇=
(l为扇形的弧长).
3.其侧面展开图扇形的半径=母线的长l
侧面展开图扇形的弧长=底面周长
圆锥的侧面展开图是扇形
S
侧
=πrl
(r表示圆锥底面的半径,
l
表示圆锥的母线长
)
28.5
弧长和扇形面积
第二十八章
圆
导入新课
讲授新课
当堂练习
课堂小结
1.理解并掌握扇形的弧长的计算公式并会进行计算.
2.理解并掌握扇形的面积的计算公式并会进行计算.
(重点)
3.能够根据圆锥侧面展开图进行相关计算.(难点)
学习目标
问题1
已知⊙O半径为R,⊙O的周长C是多少?
导入新课
回顾与思考
C=2πR
问题2
已知⊙O半径为R,⊙O的面积S是多少?
S=πR2
讲授新课
扇形的弧长
一
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线的长度),再下料,这就涉及到计算弧长的问题.
已知⊙O半径为R,求n°圆心角所对弧长.
(1)半径为R的圆,周长是多少?
C=2πR
(2)1°圆心角所对弧长是多少?
(3)n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍?
n倍
(4)n°圆心角所对弧长是多少?
l
A
B
O
n°
)
.
若设⊙O半径为R,
n°的圆心角所对的弧长为l,则
l
(1)在应用弧长公式l
,进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
l
A
B
O
n°
)
.
扇形的面积
二
已知⊙O半径为R,如何求圆心角n°的扇形的面积?
研究问题的步骤:
(1)半径为R的圆,面积是多少?
S=πR2
(2)圆心角为1°的扇形的面积是多少?
(3)圆心角为n°的扇形的面积是圆心角为1°的扇形的面积的多少倍?
n倍
(4)圆心角为n°的扇形的面积是多少?
扇形面积公式:
若设⊙O半径为R,圆心角为n°的扇形的面积S扇形,
则S扇形=
.
注意:
(1)在应用扇形的面积公式S扇形=
进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆).
问题:扇形的面积公式与弧长公式有联系吗?
想一想:扇形的面积公式与什么公式类似?
如果扇形的半径为R的圆中,圆心角为no
,那么扇形面积的计算公式为:
扇形面积的弧长与扇形面积:
合作探究
圆锥侧面展开图的相关计算
三
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点和底面圆上任一点的线段叫做圆锥的母线.
连接顶点与底面圆的圆心O的线段叫做圆锥的高.
思考圆锥的母线和圆锥的高有哪些性质?
h
l
r
由勾股定理得:
如果用r表示圆锥底面的半径,
h表示圆锥的高线长,l表示圆锥的母线长,那么r,h,l之间有怎样的数量关系呢?
r2
+
h
2
=
l
2
A
B
O
C
圆锥的侧面展开图是扇形
A
B
O
C
其侧面展开图扇形的半径=母线的长l
l
S
A
O
B
r
侧面展开图扇形的弧长=底面周长
请推导出圆锥的侧面积公式.
S
侧
=πrl
(r表示圆锥底面的半径,
l
表示圆锥的母线长
)
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
l
r
当堂练习
1.制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB的长
因此所要求的展直长度
答:管道的展直长度为2970mm.
2.圆锥形烟囱帽(如图)的母线长为80cm,高为38.7cm,求这个烟囱帽的面积(
取3.14,结果保留2个有效数字).
解:∵l=80,h=38.7
∴r=
∴S侧=πrl≈3.14×70×80≈1.8×104(cm2)
答:烟囱帽的面积约为1.8×104cm2.
l
h
r
课堂小结
1.n°的圆心角所对的弧长
.
2.圆心角为n°的扇形面积S扇=
(l为扇形的弧长).
3.其侧面展开图扇形的半径=母线的长l
侧面展开图扇形的弧长=底面周长
圆锥的侧面展开图是扇形
S
侧
=πrl
(r表示圆锥底面的半径,
l
表示圆锥的母线长
)
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
