第28章 圆 小结与复习课件 冀教版数学九年级上册(共19张ppt)
文档属性
| 名称 | 第28章 圆 小结与复习课件 冀教版数学九年级上册(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 00:00:00 | ||
图片预览


文档简介
(共19张PPT)
第二十八章
圆
知识网络
知识归纳
当堂练习
课堂小结
小结与复习
知识网络
圆的基本性质
圆
圆的对称性
弧、弦、圆心角之间的关系
同弧所对的圆周角与圆心角的关系
垂径定理及其推论
三点确定圆
有关圆的计算
垂直于弦的直径平分这条非直径的弦,
并且平分这条弦所对的两条弧
弧、弦、圆周角的对应关系
同一平面内不在同一直线上的三点
弧长
扇形的面积
圆锥的侧面积和全面积
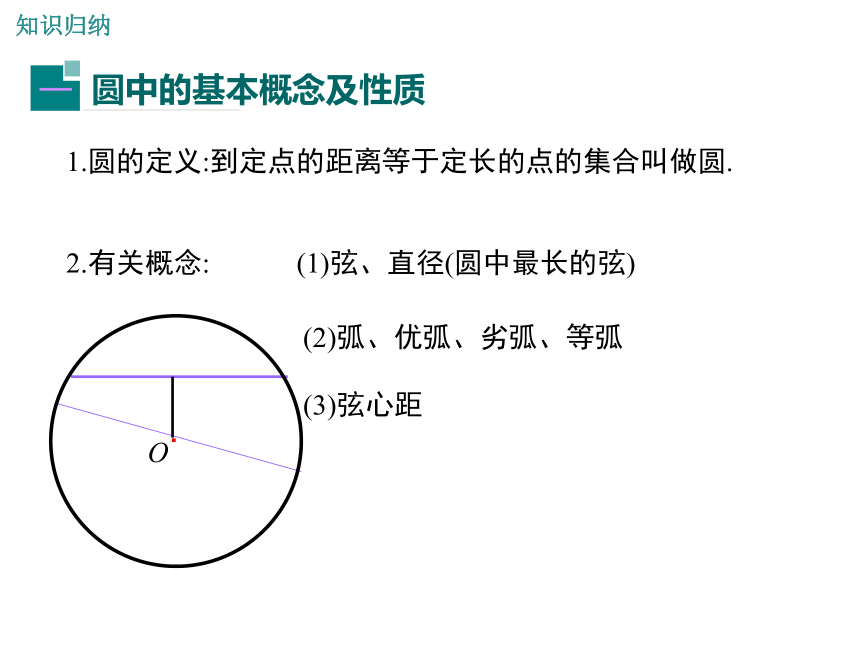
圆中的基本概念及性质
一
1.圆的定义:到定点的距离等于定长的点的集合叫做圆.
2.有关概念:
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距
.
O
知识归纳
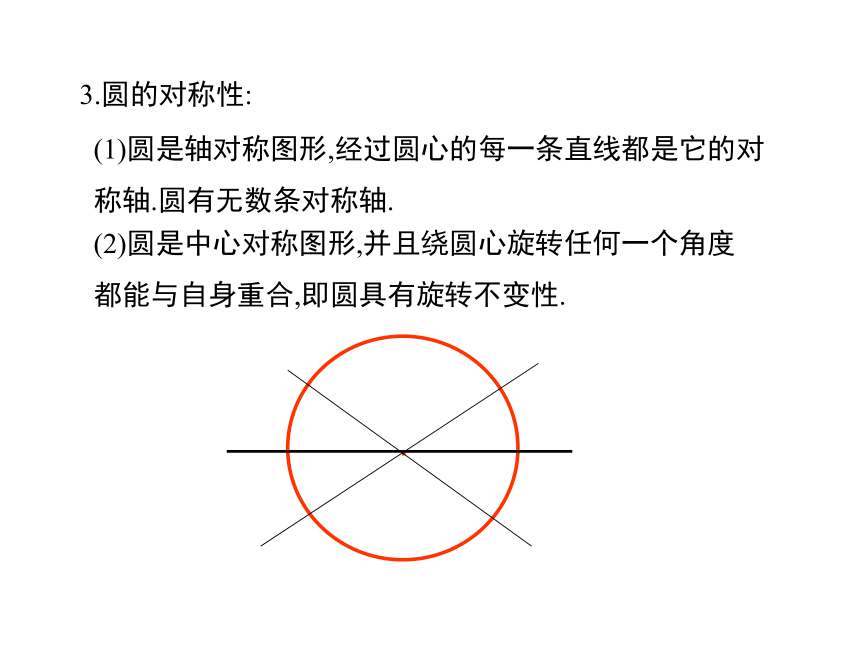
3.圆的对称性:
(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
(2)圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.
.
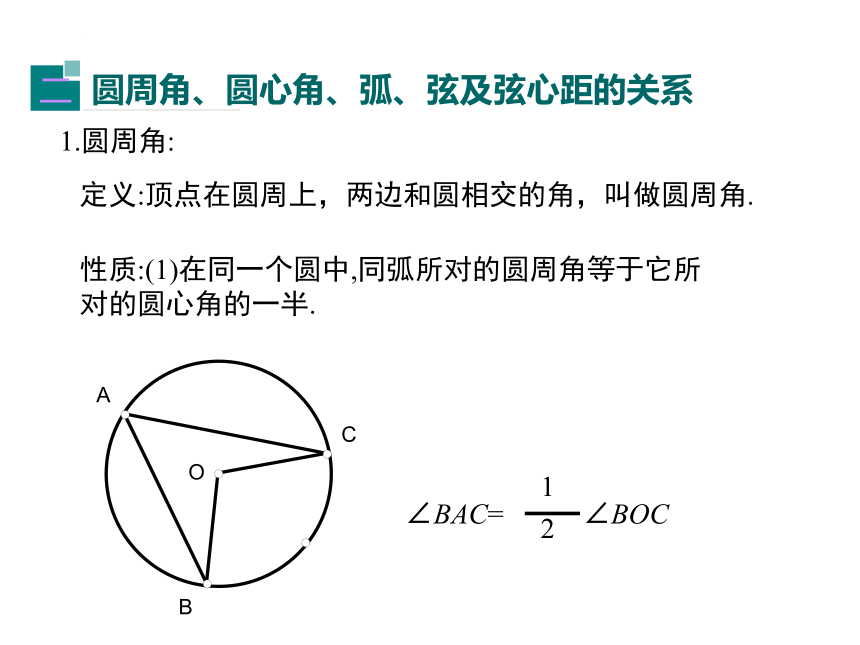
圆周角、圆心角、弧、弦及弦心距的关系
二
1.圆周角:
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
性质:(1)在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.
∠BAC=
∠BOC
1
2
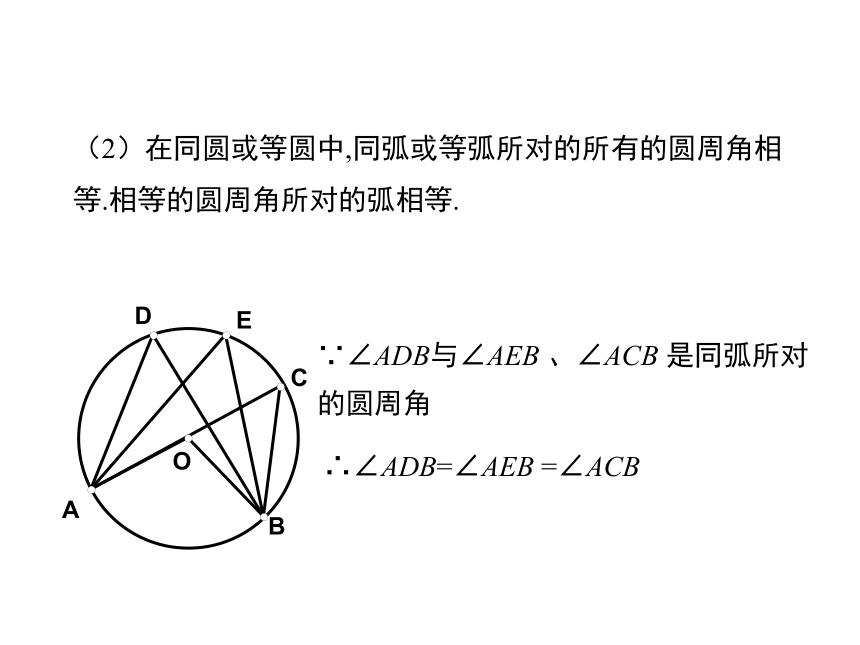
(2)在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.
∵∠ADB与∠AEB
、∠ACB
是同弧所对的圆周角
∴∠ADB=∠AEB
=∠ACB
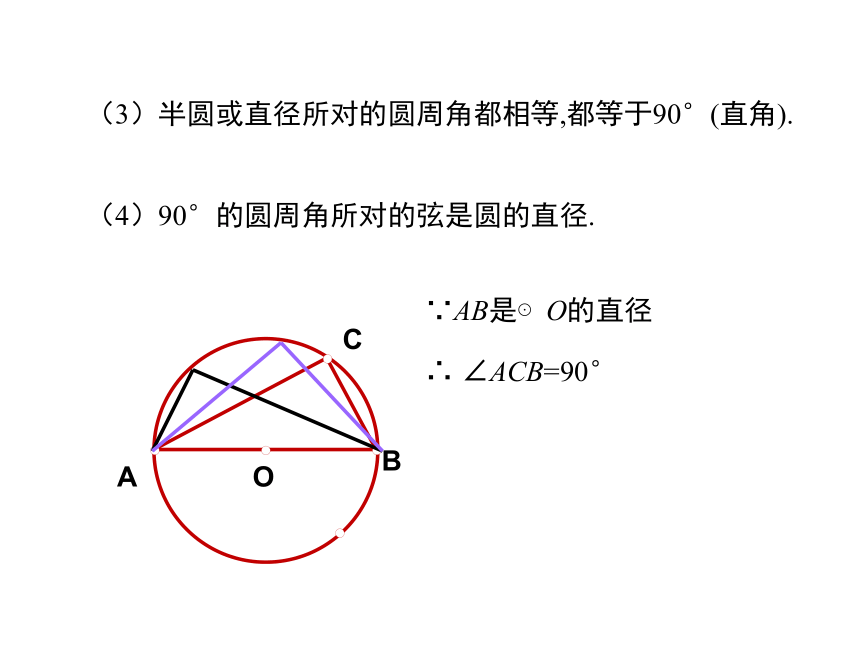
(3)半圆或直径所对的圆周角都相等,都等于90°(直角).
(4)90°的圆周角所对的弦是圆的直径.
∵AB是⊙O的直径
∴
∠ACB=90°
在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,有
一组量相等,那么它们所对应的其余各
组量都分别相等.
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④
OD=O′D′
可推出
①∠AOB=∠A′O′B′
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
C
●O
B
A
C
D
E
●O
A
B
C
90°的圆周角所对的弦是
____
.
定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
推论:直径所对的圆周角是____
.
直角
直径
垂径定理及推论
三
●O
A
B
C
D
M└
③AM=BM,
重视:模型“垂径定理直角三角形”
若
①
CD是直径
②
CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理
垂直于弦的直径平分弦,并且平分弦所的两条弧.
垂径定理的逆定理
②CD⊥AB,
由
①
CD是直径
③
AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●O
C
D
●
M
A
B
┗
平分弦(不是直径)的直径垂直于弦,并且平
分弦所对的两条弧.
合作探究
弧长和扇形面积的计算
四
(1)弧长公式:
(2)扇形面积公式:
A
B
O
C
圆锥的侧面展开图是扇形
A
B
O
C
其侧面展开图扇形的半径=母线的长l
l
S
A
O
B
r
侧面展开图扇形的弧长=底面周长
1.如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm,CD=3
cm,则圆O的半径为(
)
A.
cm
B.5
cm
C.4
cm
D.
cm
2.在☉O中,已知半径长为3,弦AB长为4,那么圆心O到AB的距离为 .
当堂练习
A
3.如图,⊙A、
⊙B、
⊙C、
⊙D两两不相交,且半径都是2cm,则图中阴影部分的面积是
.
A
B
C
D
4.如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
解:连接OC.
●
O
C
D
E
F
┗
设这段弯路的半径为Rm,则OF=(R-90)m.
根据勾股定理,得
解得R=545.
∴这段弯路的半径约为545m.
5.(1)在半径为10的圆的铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积?
(2)若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径?
(3)能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
A
B
C
①
②
③
O
解:(1)连接BC,则BC=20,
∵∠BAC=90°,AB=AC,
∴AB=AC=
∴S扇形=
(2)圆锥侧面展开图的弧长为:
(3)延长AO交⊙O于点F,交扇形于点E,EF=
最大半径为
∴不能.
A
B
C
①
②
③
O
课堂小结
圆的基本性质
圆
圆的对称性
弧、弦圆心角之间的关系
同弧上的圆周角与圆心角的关系
垂径定理及其推论
三点确定圆
有关圆的计算
垂直于弦的直径平分这条弦,并且平分这
条弦所对的两条弧
弧、弦、圆周角的对应关系
同一平面内不在同一直线上的
弧长
扇形的面积
圆锥的侧面积和全面积
第二十八章
圆
知识网络
知识归纳
当堂练习
课堂小结
小结与复习
知识网络
圆的基本性质
圆
圆的对称性
弧、弦、圆心角之间的关系
同弧所对的圆周角与圆心角的关系
垂径定理及其推论
三点确定圆
有关圆的计算
垂直于弦的直径平分这条非直径的弦,
并且平分这条弦所对的两条弧
弧、弦、圆周角的对应关系
同一平面内不在同一直线上的三点
弧长
扇形的面积
圆锥的侧面积和全面积
圆中的基本概念及性质
一
1.圆的定义:到定点的距离等于定长的点的集合叫做圆.
2.有关概念:
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距
.
O
知识归纳
3.圆的对称性:
(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
(2)圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.
.
圆周角、圆心角、弧、弦及弦心距的关系
二
1.圆周角:
定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.
性质:(1)在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.
∠BAC=
∠BOC
1
2
(2)在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.
∵∠ADB与∠AEB
、∠ACB
是同弧所对的圆周角
∴∠ADB=∠AEB
=∠ACB
(3)半圆或直径所对的圆周角都相等,都等于90°(直角).
(4)90°的圆周角所对的弦是圆的直径.
∵AB是⊙O的直径
∴
∠ACB=90°
在同圆或等圆中,如果①两个圆心角,
②两条弧,③两条弦,④两条弦心距中,有
一组量相等,那么它们所对应的其余各
组量都分别相等.
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④
OD=O′D′
可推出
①∠AOB=∠A′O′B′
●O
A
B
┓
D
A′
B′
D′
┏
●O
A
B
C
●O
B
A
C
D
E
●O
A
B
C
90°的圆周角所对的弦是
____
.
定理:
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
推论:直径所对的圆周角是____
.
直角
直径
垂径定理及推论
三
●O
A
B
C
D
M└
③AM=BM,
重视:模型“垂径定理直角三角形”
若
①
CD是直径
②
CD⊥AB
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
垂径定理
垂直于弦的直径平分弦,并且平分弦所的两条弧.
垂径定理的逆定理
②CD⊥AB,
由
①
CD是直径
③
AM=BM
可推得
⌒
⌒
④AC=BC,
⌒
⌒
⑤AD=BD.
●O
C
D
●
M
A
B
┗
平分弦(不是直径)的直径垂直于弦,并且平
分弦所对的两条弧.
合作探究
弧长和扇形面积的计算
四
(1)弧长公式:
(2)扇形面积公式:
A
B
O
C
圆锥的侧面展开图是扇形
A
B
O
C
其侧面展开图扇形的半径=母线的长l
l
S
A
O
B
r
侧面展开图扇形的弧长=底面周长
1.如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8cm,CD=3
cm,则圆O的半径为(
)
A.
cm
B.5
cm
C.4
cm
D.
cm
2.在☉O中,已知半径长为3,弦AB长为4,那么圆心O到AB的距离为 .
当堂练习
A
3.如图,⊙A、
⊙B、
⊙C、
⊙D两两不相交,且半径都是2cm,则图中阴影部分的面积是
.
A
B
C
D
4.如图,一条公路的转弯处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD,垂足为F,EF=90m.求这段弯路的半径.
解:连接OC.
●
O
C
D
E
F
┗
设这段弯路的半径为Rm,则OF=(R-90)m.
根据勾股定理,得
解得R=545.
∴这段弯路的半径约为545m.
5.(1)在半径为10的圆的铁片中,要裁剪出一个直角扇形,求能裁剪出的最大的直角扇形的面积?
(2)若用这个最大的直角扇形恰好围成一个圆锥,求这个圆锥的底面圆的半径?
(3)能否从最大的余料③中剪出一个圆做该圆锥的底面?请说明理由.
A
B
C
①
②
③
O
解:(1)连接BC,则BC=20,
∵∠BAC=90°,AB=AC,
∴AB=AC=
∴S扇形=
(2)圆锥侧面展开图的弧长为:
(3)延长AO交⊙O于点F,交扇形于点E,EF=
最大半径为
∴不能.
A
B
C
①
②
③
O
课堂小结
圆的基本性质
圆
圆的对称性
弧、弦圆心角之间的关系
同弧上的圆周角与圆心角的关系
垂径定理及其推论
三点确定圆
有关圆的计算
垂直于弦的直径平分这条弦,并且平分这
条弦所对的两条弧
弧、弦、圆周角的对应关系
同一平面内不在同一直线上的
弧长
扇形的面积
圆锥的侧面积和全面积
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
