冀教版数学九年级上册26.1锐角三角函数(2)课件(共19张PPT)
文档属性
| 名称 | 冀教版数学九年级上册26.1锐角三角函数(2)课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 405.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 08:16:55 | ||
图片预览



文档简介
(共19张PPT)
第二十六章
解直角三角形
26.1
锐角三角函数(2)
学习目标:
1、经历正弦、余弦概念的形成过程,理解三角
函数的定义,并能根据正弦、余弦的概念进
行计算.
2、经历探索30°,45°,60°角的正弦、余弦
值的过程,能够进行有关推理,并能进行含
有30°,45°,60°角的三角函数值的计算.
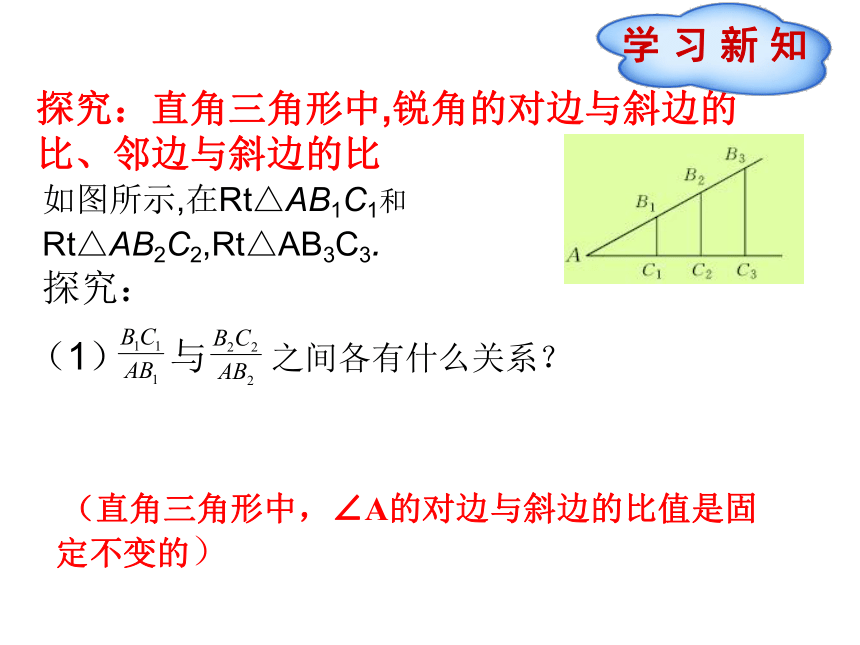
探究:直角三角形中,锐角的对边与斜边的比、邻边与斜边的比
如图所示,在Rt△AB1C1和
Rt△AB2C2,Rt△AB3C3.
探究:
(1)
与
之间各有什么关系?
学
习
新
知
(直角三角形中,∠A的对边与斜边的比值是固定不变的)
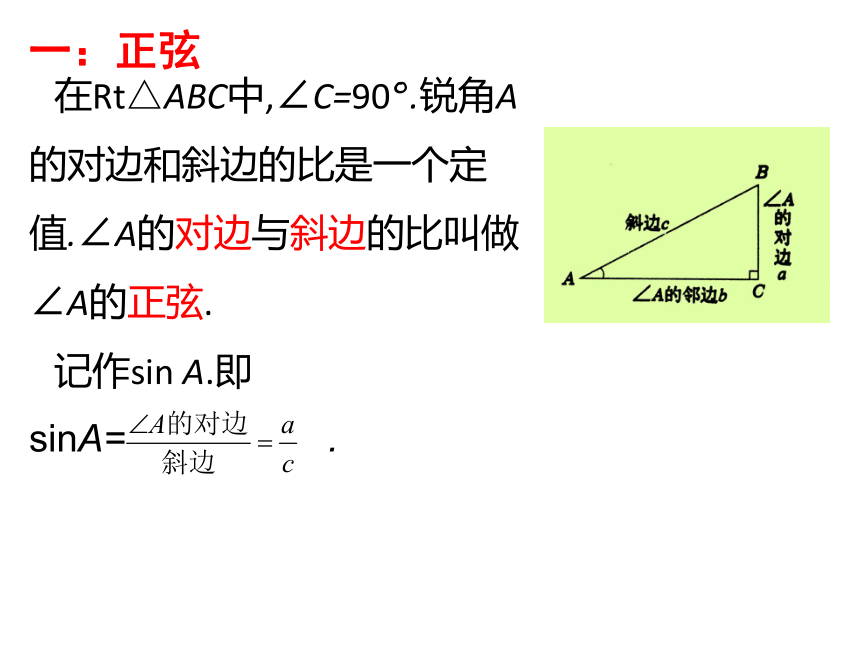
在Rt△ABC中,∠C=90°.锐角A的对边和斜边的比是一个定值.∠A的对边与斜边的比叫做∠A的正弦.
记作sin
A.即sinA=
.
一:正弦
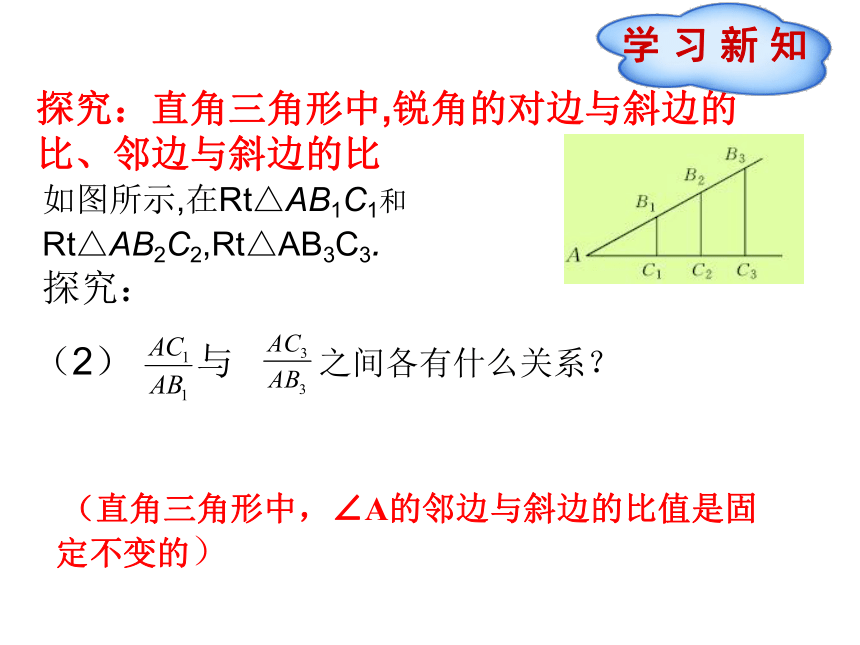
探究:直角三角形中,锐角的对边与斜边的比、邻边与斜边的比
如图所示,在Rt△AB1C1和
Rt△AB2C2,Rt△AB3C3.
探究:
(直角三角形中,∠A的邻边与斜边的比值是固定不变的)
学
习
新
知
(2)
与
之间各有什么关系?
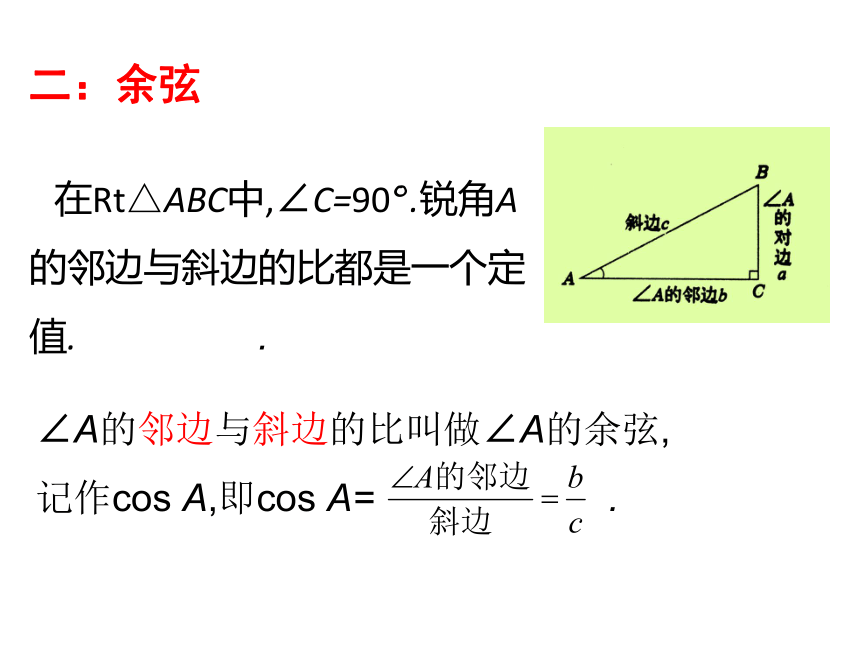
在Rt△ABC中,∠C=90°.锐角A的邻边与斜边的比都是一个定值.
.
二:余弦
∠A的邻边与斜边的比叫做∠A的余弦,记作cos
A,即cos
A=
.
观察两个不同大小的三角板,当角是30°、45°、60°时,它们的对边与斜边、邻边与斜边的比值有什么规律?分别求出这些角的正弦和余弦.
问题思考
三:特殊角的三角函数值
α
30°
45°
60°
sin
α
cos
α
tan
α
1
【思考】 观察表格中特殊角的三角函数值,你能发现什么结论?
(3)0A<1,0A<1.
结论
(1)正弦、正切值随着角度的增大而增大,余弦值随着角度的增大而减小.
(2)sin
30°=cos
60°,
sin
60°=cos
30°,
sin
45°=cos
45°,
由此可知sin
α=cos
(90°-α),
cos
α=sin
(90°-α).
【归纳:】
我们把锐角α正弦、余弦和正切统称为α的三角函数.
为方便起见,今后将(sin
α)2,(cos
α)2,(tan
α)2分别记作sin2
α
cos2
α,tan2
α.
求下列各式的值:
(1)2sin
30°+3tan
30°-tan
45°;
(2)(sin
45°)2+tan
60°sin
60°.
解:(1)2sin
30°+3tan
30°-tan
45°
=
.
(2)(sin
45°)2+tan
60°sin
60°
=
.
[巩固提高]
2、如图所示,在Rt△ABC中,∠C=90°,AC=5,BC=12.求sin
A,cos
A,
tan
A的值.
解:∵
.
∴
,
,
.
3.当用三个字母表示角时,角的符号“∠”不能省略,如sin∠ABC.
[知识拓展]
1.正弦和余弦都是一个比值,没有单位.
2.正弦值和余弦值只与角的大小有关,与三角形的大小无关.
谈收获
1.三角形在正方形方格纸巾中的位置如图所示,则sin
α的值是
( )
C
检测反馈
2.在Rt△ABC中,∠C=90°,AB=13,
AC=12,则下列各式正确的是( )
A.sinA=
D.以上都不对
B.cos
A=
C.tan
A=
B
3.在Rt△ABC中,∠C=90°,sin
A=
,
AB=20,则BC= .?
解析:∵AB=20,sinA=
,
∴sinA=
,∴BC=
×20=12.故填12.
12
4.在△ABC中,sinA=
,cosB=
,则△ABC的形状为
三角形.
解析:∵sin
A=
,cos
B=
,
∴∠A=30°,∠B=45°,又∠A+∠B+∠C=180°,∴∠C=105°,∴△ABC为钝角三角形.故填钝角.
钝角
5.在△ABC中,∠C=90°,cos
A=
,AB=12,求△ABC的面积.
解:∵cos
A=
=
,AB=12,∴AC=4
.
由勾股定理可得BC=
∴S△ABC=
AC·BC=
×4
×4
=24
.
6.计算:
(1)
;
(2)tan230°-sin
60°·cos
30°.
第二十六章
解直角三角形
26.1
锐角三角函数(2)
学习目标:
1、经历正弦、余弦概念的形成过程,理解三角
函数的定义,并能根据正弦、余弦的概念进
行计算.
2、经历探索30°,45°,60°角的正弦、余弦
值的过程,能够进行有关推理,并能进行含
有30°,45°,60°角的三角函数值的计算.
探究:直角三角形中,锐角的对边与斜边的比、邻边与斜边的比
如图所示,在Rt△AB1C1和
Rt△AB2C2,Rt△AB3C3.
探究:
(1)
与
之间各有什么关系?
学
习
新
知
(直角三角形中,∠A的对边与斜边的比值是固定不变的)
在Rt△ABC中,∠C=90°.锐角A的对边和斜边的比是一个定值.∠A的对边与斜边的比叫做∠A的正弦.
记作sin
A.即sinA=
.
一:正弦
探究:直角三角形中,锐角的对边与斜边的比、邻边与斜边的比
如图所示,在Rt△AB1C1和
Rt△AB2C2,Rt△AB3C3.
探究:
(直角三角形中,∠A的邻边与斜边的比值是固定不变的)
学
习
新
知
(2)
与
之间各有什么关系?
在Rt△ABC中,∠C=90°.锐角A的邻边与斜边的比都是一个定值.
.
二:余弦
∠A的邻边与斜边的比叫做∠A的余弦,记作cos
A,即cos
A=
.
观察两个不同大小的三角板,当角是30°、45°、60°时,它们的对边与斜边、邻边与斜边的比值有什么规律?分别求出这些角的正弦和余弦.
问题思考
三:特殊角的三角函数值
α
30°
45°
60°
sin
α
cos
α
tan
α
1
【思考】 观察表格中特殊角的三角函数值,你能发现什么结论?
(3)0
结论
(1)正弦、正切值随着角度的增大而增大,余弦值随着角度的增大而减小.
(2)sin
30°=cos
60°,
sin
60°=cos
30°,
sin
45°=cos
45°,
由此可知sin
α=cos
(90°-α),
cos
α=sin
(90°-α).
【归纳:】
我们把锐角α正弦、余弦和正切统称为α的三角函数.
为方便起见,今后将(sin
α)2,(cos
α)2,(tan
α)2分别记作sin2
α
cos2
α,tan2
α.
求下列各式的值:
(1)2sin
30°+3tan
30°-tan
45°;
(2)(sin
45°)2+tan
60°sin
60°.
解:(1)2sin
30°+3tan
30°-tan
45°
=
.
(2)(sin
45°)2+tan
60°sin
60°
=
.
[巩固提高]
2、如图所示,在Rt△ABC中,∠C=90°,AC=5,BC=12.求sin
A,cos
A,
tan
A的值.
解:∵
.
∴
,
,
.
3.当用三个字母表示角时,角的符号“∠”不能省略,如sin∠ABC.
[知识拓展]
1.正弦和余弦都是一个比值,没有单位.
2.正弦值和余弦值只与角的大小有关,与三角形的大小无关.
谈收获
1.三角形在正方形方格纸巾中的位置如图所示,则sin
α的值是
( )
C
检测反馈
2.在Rt△ABC中,∠C=90°,AB=13,
AC=12,则下列各式正确的是( )
A.sinA=
D.以上都不对
B.cos
A=
C.tan
A=
B
3.在Rt△ABC中,∠C=90°,sin
A=
,
AB=20,则BC= .?
解析:∵AB=20,sinA=
,
∴sinA=
,∴BC=
×20=12.故填12.
12
4.在△ABC中,sinA=
,cosB=
,则△ABC的形状为
三角形.
解析:∵sin
A=
,cos
B=
,
∴∠A=30°,∠B=45°,又∠A+∠B+∠C=180°,∴∠C=105°,∴△ABC为钝角三角形.故填钝角.
钝角
5.在△ABC中,∠C=90°,cos
A=
,AB=12,求△ABC的面积.
解:∵cos
A=
=
,AB=12,∴AC=4
.
由勾股定理可得BC=
∴S△ABC=
AC·BC=
×4
×4
=24
.
6.计算:
(1)
;
(2)tan230°-sin
60°·cos
30°.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
