冀教版数学九年级上册26.3解直角三角形 课件(共19张PPT)
文档属性
| 名称 | 冀教版数学九年级上册26.3解直角三角形 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 08:18:41 | ||
图片预览




文档简介
(共19张PPT)
九年级数学(上册)第二十六章
§26.3
解直角三角形
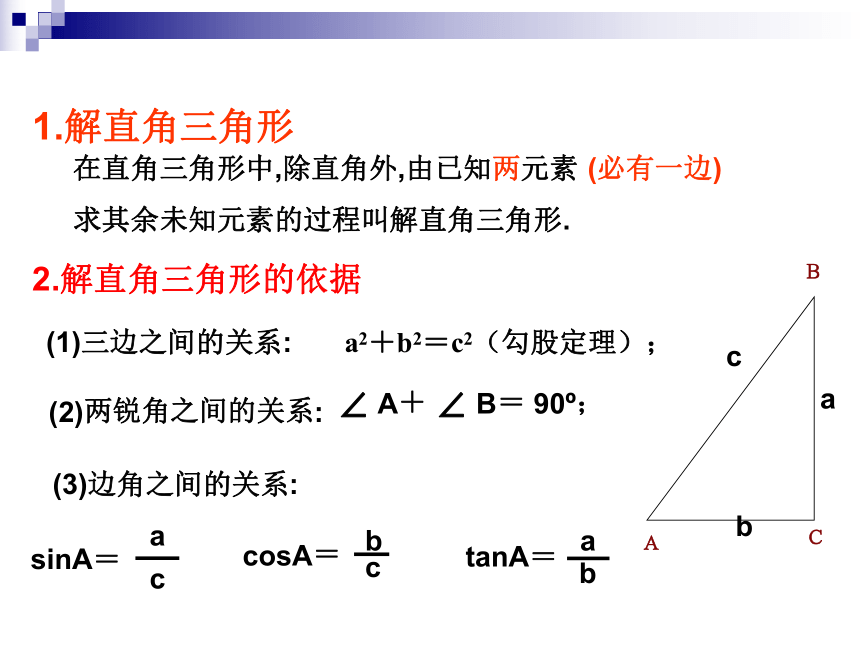
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠
A+
∠
B=
90?;
(3)边角之间的关系:
A
C
B
a
b
c
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
3.互余两角之间的三角函数关系:
两锐角
则∠A
、
∠
B的三角函数有如下关系:
sinA=cosB,
cosA=sinB,
tanA
tanB=1.
4.同角之间的三角函数关系:
sin2α+cos2α=1.
α
α
α
其中的α表示锐角
复习
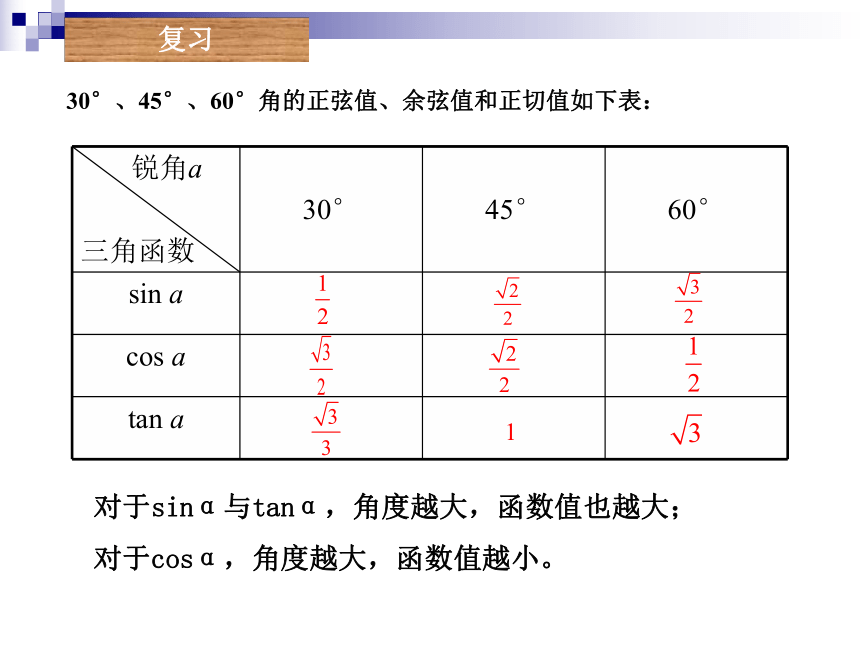
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小。
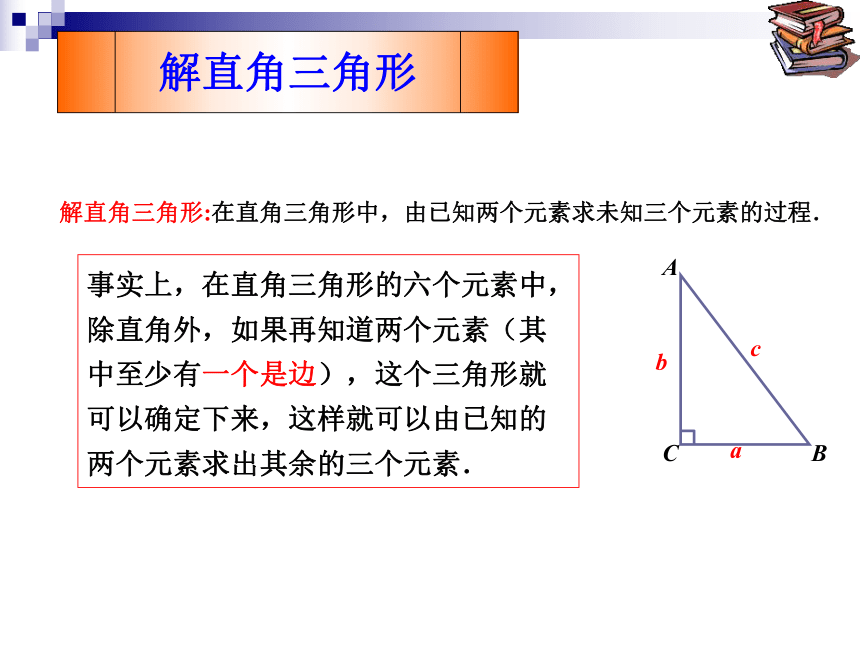
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知两个元素求未知三个元素的过程.
解直角三角形
例1
如图,在Rt△ABC中,∠C=90°,
解这个直角三角形
解:
A
B
C
在Rt△ABC中:
例2
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
解:在Rt△ABC中,∠A=90°-∠B=90°-35°=55°
A
B
C
a
b
c
20
35°
你还有其他方法求出c吗?
tan35?≈0.7002
sin35
?≈0.5735
例3
如图,在Rt△ABC中,∠C=90°,AC=6,
∠BAC的平分线
,解这个直角三角形。
D
A
B
C
6
解:
∵AD平分∠BAC
在Rt△ADC中
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a
=
30
,
b
=
20
;
练习
解:根据勾股定理
A
B
C
b=20
a=30
c
(tan55?≈1.4
tan56?
≈1.5)
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(2)
∠B=60°,c
=
14.
A
B
C
b
a
c=14
解:
解决有关比萨斜塔倾斜的问题.
设塔顶中心点为B,塔身中心线BA与垂直中心线CA的夹角为
,过B点向垂直中心线引垂线
于点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
所以∠A≈5°28′
Sin5°28′≈0.0954
A
B
C
A
B
C
--------本章引例
解直角
三角形
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
1.
在Rt△ABC中∠C=90°,当
锐角A>45°时,sinA的值(
)
(A)0<sinA<
(B)
<sinA<1
(C)
0<sinA<
(D)
<sinA<1
B
综合练习
(一)填空选择题:
2.当∠A为锐角,且cosA=
,那么(
)
(A)0°<∠A<
30
°
(B)
30°<∠A≤45°
(C)45°<∠A≤
60
°
(D)
60°<∠A<
90
°
D
3.在△ABC中∠C=90°
∠B=2∠A
,
则cosA=______
5.已A是锐角且tanA=3,则
4.
若tan(β+20°)=
(β为锐角),
则β=________
40°
1.在Rt△ABC中,已知∠C
=
90°
,
a=12,
c
=24
.
解这个直角三角形
2.在Rt△ABC
中,∠C
=
90
°.
(l)已知c
=
15
,∠
B
=
60°
,求a
;
(2)已知∠A=30
°
,a=24
,求b
,
c
.
3
12
=
b
,
∠A=30
°,
∠
B
=
60°
.
(1)a=7.5
(2)b=24
c=48
3.
如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
A
B
C
30°
地面
太阳光线
60°
30
AB的长
D
5.如图2,在离铁塔BE
120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE=
_________
(根号保留).
图1
图2
4.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为
m,则下面结论中正确的是(
)
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°
C
九年级数学(上册)第二十六章
§26.3
解直角三角形
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠
A+
∠
B=
90?;
(3)边角之间的关系:
A
C
B
a
b
c
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
3.互余两角之间的三角函数关系:
两锐角
则∠A
、
∠
B的三角函数有如下关系:
sinA=cosB,
cosA=sinB,
tanA
tanB=1.
4.同角之间的三角函数关系:
sin2α+cos2α=1.
α
α
α
其中的α表示锐角
复习
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
对于sinα与tanα,角度越大,函数值也越大;
对于cosα,角度越大,函数值越小。
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
A
B
a
b
c
C
解直角三角形:在直角三角形中,由已知两个元素求未知三个元素的过程.
解直角三角形
例1
如图,在Rt△ABC中,∠C=90°,
解这个直角三角形
解:
A
B
C
在Rt△ABC中:
例2
如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
解:在Rt△ABC中,∠A=90°-∠B=90°-35°=55°
A
B
C
a
b
c
20
35°
你还有其他方法求出c吗?
tan35?≈0.7002
sin35
?≈0.5735
例3
如图,在Rt△ABC中,∠C=90°,AC=6,
∠BAC的平分线
,解这个直角三角形。
D
A
B
C
6
解:
∵AD平分∠BAC
在Rt△ADC中
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(1)a
=
30
,
b
=
20
;
练习
解:根据勾股定理
A
B
C
b=20
a=30
c
(tan55?≈1.4
tan56?
≈1.5)
在Rt△ABC中,∠C=90°,根据下列条件解直角三角形;
(2)
∠B=60°,c
=
14.
A
B
C
b
a
c=14
解:
解决有关比萨斜塔倾斜的问题.
设塔顶中心点为B,塔身中心线BA与垂直中心线CA的夹角为
,过B点向垂直中心线引垂线
于点C(如图),在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m
所以∠A≈5°28′
Sin5°28′≈0.0954
A
B
C
A
B
C
--------本章引例
解直角
三角形
∠A+
∠
B=90°
a2+b2=c2
三角函数
关系式
计算器
由锐角求三角函数值
由三角函数值求锐角
归纳小结
解直角三角形:
由已知元素求未知元素的过程
直角三角形中,
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
1.
在Rt△ABC中∠C=90°,当
锐角A>45°时,sinA的值(
)
(A)0<sinA<
(B)
<sinA<1
(C)
0<sinA<
(D)
<sinA<1
B
综合练习
(一)填空选择题:
2.当∠A为锐角,且cosA=
,那么(
)
(A)0°<∠A<
30
°
(B)
30°<∠A≤45°
(C)45°<∠A≤
60
°
(D)
60°<∠A<
90
°
D
3.在△ABC中∠C=90°
∠B=2∠A
,
则cosA=______
5.已A是锐角且tanA=3,则
4.
若tan(β+20°)=
(β为锐角),
则β=________
40°
1.在Rt△ABC中,已知∠C
=
90°
,
a=12,
c
=24
.
解这个直角三角形
2.在Rt△ABC
中,∠C
=
90
°.
(l)已知c
=
15
,∠
B
=
60°
,求a
;
(2)已知∠A=30
°
,a=24
,求b
,
c
.
3
12
=
b
,
∠A=30
°,
∠
B
=
60°
.
(1)a=7.5
(2)b=24
c=48
3.
如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
A
B
C
30°
地面
太阳光线
60°
30
AB的长
D
5.如图2,在离铁塔BE
120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE=
_________
(根号保留).
图1
图2
4.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为
m,则下面结论中正确的是(
)
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°
C
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
