3 倒数(课件) 数学六年级上册-西师大版(共32张PPT)
文档属性
| 名称 | 3 倒数(课件) 数学六年级上册-西师大版(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 07:32:43 | ||
图片预览








文档简介
(共32张PPT)
倒数的认识
吞
吴
杏
呆
土
干
一、找规律:
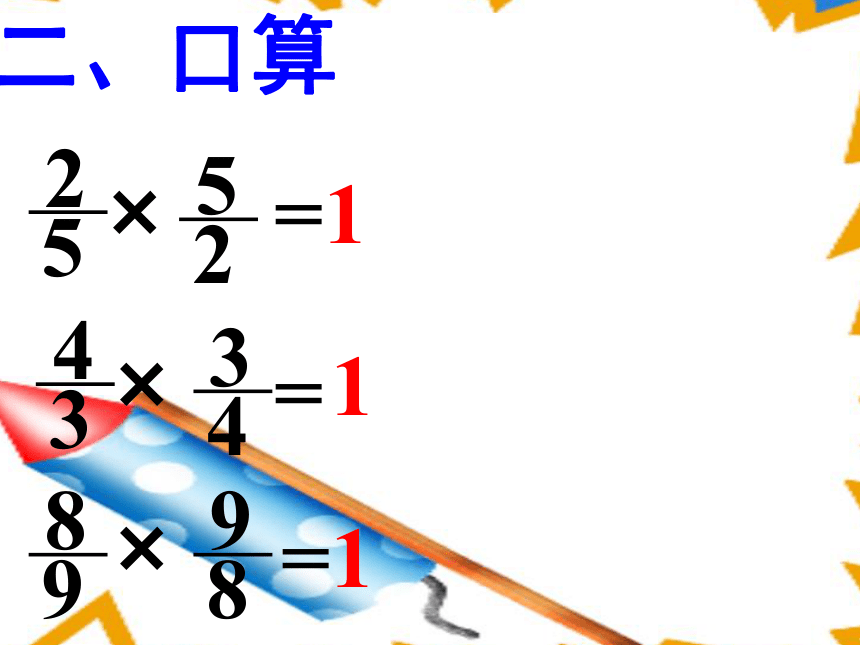
二、口算
5
2
2
5
×
9
8
8
9
4
3
=
1
=
×
=
×
1
1
3
4
观察算式和结果,你有什么发现?
同桌讨论:
1、分子、分母交换了位置;
2、乘积都为1;
3、都是两个数相乘。
1.什么叫倒数?
是1的
叫做
倒数。
乘积
两个数
互为
乘积
两个数
互为
乘积是1的两个数互为倒数。例如,
和
的乘积是1,我们就说
和
互为倒数,也可以说成
的倒数是
,
的倒数是
,还可以说
是
的倒
数,
是
的倒数。
和是1的两个数互为倒数。(
)
差是1的两个数互为倒数。(
)
商是1的两个数互为倒数。(
)
得数是1的两个数互为倒数。(
)
乘积是1的几个数互为倒数。(
)
乘积是1的两个数是倒数。(
)
×
×
×
×
×
×
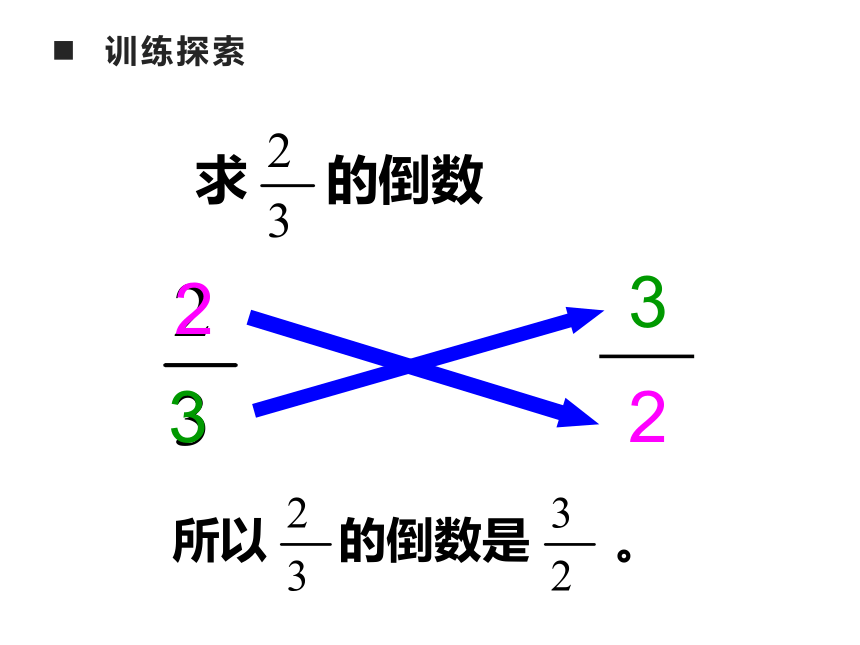
训练探索
所以
的倒数是
。
求
的倒数
3
2
3
2
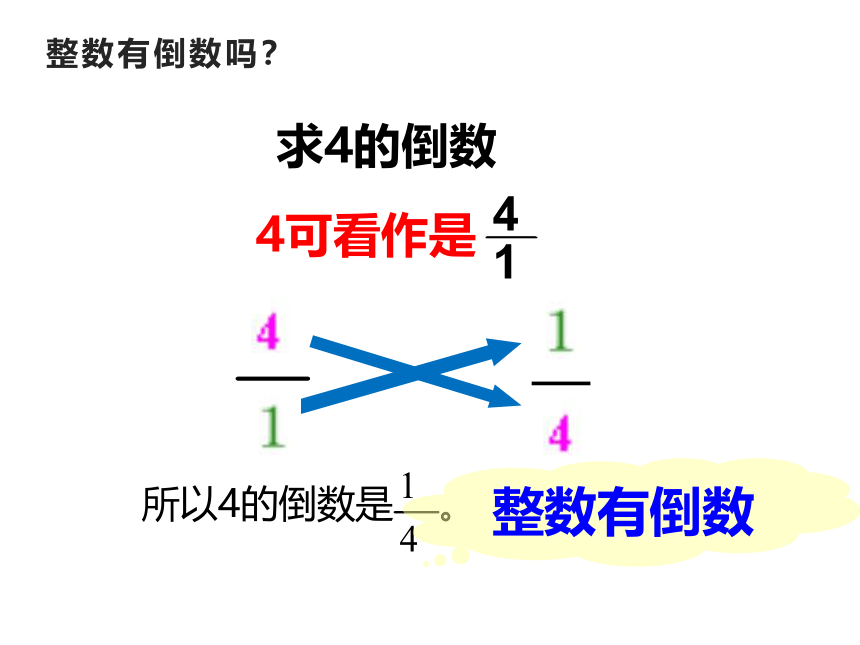
整数有倒数吗?
求4的倒数
所以4的倒数是
。
4可看作是
4
1
整数有倒数
若用字母a表示任意一个自然数,那么它的倒数该怎样表示?有没有什么特殊的规定?
a的倒数为1/a(a不为0)。
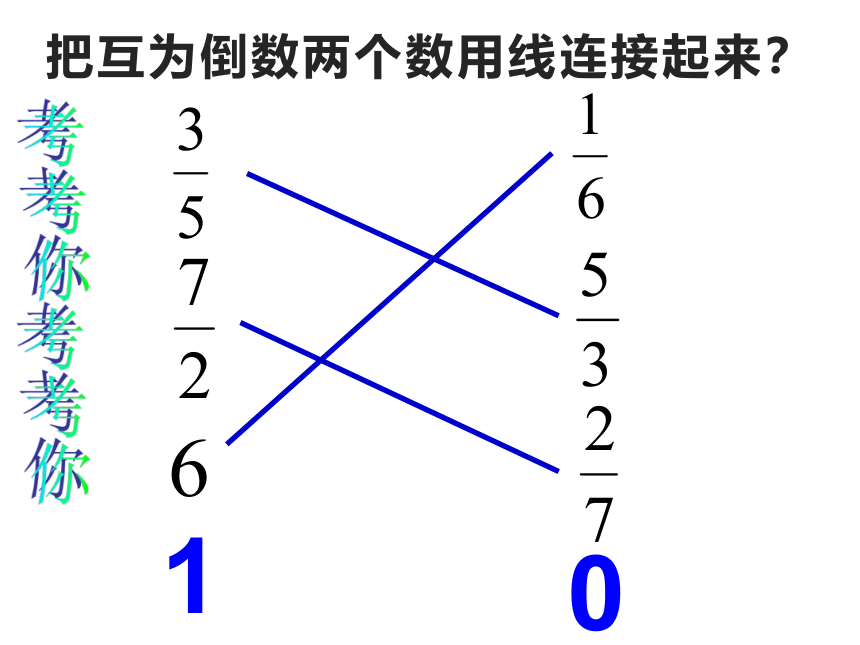
把互为倒数两个数用线连接起来?
1
0
⑴
1的倒数是(
)。
⑵
0有没有倒数,为什么?
①
0
作分母无意义。
②
0
×(
任何数
)
≠1
讨论:
0
没有倒数,因为:
提问:怎样求一个数的倒数?
求一个数
的倒数,只要把这个
数的分子、分母调换位置。
(0除外)
拓展延伸:
怎样求小数的倒数?
0.75
先化成分数
再调换分子、分母的位置
__
4
3
0.75的倒数是
__
3
4
_
3
4
拓展延伸:
怎样求带分数的倒数?
先化成假分数
再调换分子、分母的位置
__
2
8
3
的倒数是
__
2
8
3
__
8
19
__
8
19
__
19
8
我来考考你
1
的倒数是(
)
2
的倒数是(
)
0.3的倒数是(
)
0.5的倒数是(
)
2
求一个数(
)的倒数,可以把
。
0除外
这个数的分子、分母调换位置
1.
填空:
(1)乘积是(
)的两个数互为倒数。
(2)(
)的倒数是它本身,(
)没有倒数。
(3)A和B互为倒数,则A·B=(
)。
(4)0.7的倒数是(
)。
1
1
0
1
判断对错
1.
0的倒数是0。
2.
是倒数。
3.
小数没有倒数。
4.
和
互为倒数。
5.
的倒数是
。
2
5
2
1
2
3
2
7
7
2
5
7
(
)
(
)
(
)
(
)
(
)
2.判断。
(1)
是倒数。(
)
(2)一个数的倒数一定比原来小。(
)
(3)所有的数都有倒数。(
)
(4)a是整数,所以a的倒数是
。(
)
(5)一位同学写
的倒数时这样书写:
=
。
(6)因为0.2×5=1,所以0.2和5互为倒数。
(
)
⑴
的倒数是(
)
。
(2)
的倒数是(
)
。
⑶
的倒数是(
)
。
(4)
的倒数是(
)
。
(5)
1
的倒数是(
)
。
1、说出下列各数的倒数。
(6)
的倒数是(
)
。
4
×(
)=
×(
)=0.25
×(
)=
×
2
4
3、
先找出每组数中各数的倒数,再看看能发现什么
?
我的发现
⑴
真分数的倒数一定大于
1
。
我的发现
4
3
5
2
9
7
先找出每组数中各数的倒数,再看看能发现什么
?
大于
1
的假分数的倒数一定小于
1
。
⑵
我的发现
2
7
5
9
6
13
先找出每组数中各数的倒数,再看看能发现什么
?
⑶
分子是1的分数的倒数一定是整数
。
我的发现
2
10
12
先找出每组数中各数的倒数,再看看能发现什么
?
⑴
真分数的倒数一定大于
1
。
大于
1
的假分数的倒数一定小于
1
。
整数(0除外)的倒数的分子一定是
1
。
⑵
⑷
⑶
分子是1的分数的倒数一定是整数
。
我的发现
先找出每组数中各数的倒数,再看看能发现什么
?
训练发展
1.
乘积是1
的
两个数
叫做
互为
倒数。
乘积是1
两个数
互为
2.
求一个数
的倒数,只要把这个数的分子、分母调换位置。
(0除外)
4.
求整数的倒数,先把整数看成分母是1的分数,再分子、分母调换位置。
3.
0没有倒数,1的倒数是它本身1。
5.
求小数的倒数,先把小数化成分数,再分子、分母调换位置。
训练发展
7.
真分数的倒数一定大于1;
大于1的假分数的倒数一定小于1;
分子是1的分数,它的倒数一定是整数;
不为0的整数,它的倒数的分子一定是1。
6.
求带分数的倒数,先把带分数化成假分数,再分子、分母调换位置。
1、
的倒数的
是多少?
2、最大的两位数与最小的两位数的和的倒数是多少?
总结:今天我们学习了什么知识?你有什么收获?还有什么问题吗?
倒数的认识
吞
吴
杏
呆
土
干
一、找规律:
二、口算
5
2
2
5
×
9
8
8
9
4
3
=
1
=
×
=
×
1
1
3
4
观察算式和结果,你有什么发现?
同桌讨论:
1、分子、分母交换了位置;
2、乘积都为1;
3、都是两个数相乘。
1.什么叫倒数?
是1的
叫做
倒数。
乘积
两个数
互为
乘积
两个数
互为
乘积是1的两个数互为倒数。例如,
和
的乘积是1,我们就说
和
互为倒数,也可以说成
的倒数是
,
的倒数是
,还可以说
是
的倒
数,
是
的倒数。
和是1的两个数互为倒数。(
)
差是1的两个数互为倒数。(
)
商是1的两个数互为倒数。(
)
得数是1的两个数互为倒数。(
)
乘积是1的几个数互为倒数。(
)
乘积是1的两个数是倒数。(
)
×
×
×
×
×
×
训练探索
所以
的倒数是
。
求
的倒数
3
2
3
2
整数有倒数吗?
求4的倒数
所以4的倒数是
。
4可看作是
4
1
整数有倒数
若用字母a表示任意一个自然数,那么它的倒数该怎样表示?有没有什么特殊的规定?
a的倒数为1/a(a不为0)。
把互为倒数两个数用线连接起来?
1
0
⑴
1的倒数是(
)。
⑵
0有没有倒数,为什么?
①
0
作分母无意义。
②
0
×(
任何数
)
≠1
讨论:
0
没有倒数,因为:
提问:怎样求一个数的倒数?
求一个数
的倒数,只要把这个
数的分子、分母调换位置。
(0除外)
拓展延伸:
怎样求小数的倒数?
0.75
先化成分数
再调换分子、分母的位置
__
4
3
0.75的倒数是
__
3
4
_
3
4
拓展延伸:
怎样求带分数的倒数?
先化成假分数
再调换分子、分母的位置
__
2
8
3
的倒数是
__
2
8
3
__
8
19
__
8
19
__
19
8
我来考考你
1
的倒数是(
)
2
的倒数是(
)
0.3的倒数是(
)
0.5的倒数是(
)
2
求一个数(
)的倒数,可以把
。
0除外
这个数的分子、分母调换位置
1.
填空:
(1)乘积是(
)的两个数互为倒数。
(2)(
)的倒数是它本身,(
)没有倒数。
(3)A和B互为倒数,则A·B=(
)。
(4)0.7的倒数是(
)。
1
1
0
1
判断对错
1.
0的倒数是0。
2.
是倒数。
3.
小数没有倒数。
4.
和
互为倒数。
5.
的倒数是
。
2
5
2
1
2
3
2
7
7
2
5
7
(
)
(
)
(
)
(
)
(
)
2.判断。
(1)
是倒数。(
)
(2)一个数的倒数一定比原来小。(
)
(3)所有的数都有倒数。(
)
(4)a是整数,所以a的倒数是
。(
)
(5)一位同学写
的倒数时这样书写:
=
。
(6)因为0.2×5=1,所以0.2和5互为倒数。
(
)
⑴
的倒数是(
)
。
(2)
的倒数是(
)
。
⑶
的倒数是(
)
。
(4)
的倒数是(
)
。
(5)
1
的倒数是(
)
。
1、说出下列各数的倒数。
(6)
的倒数是(
)
。
4
×(
)=
×(
)=0.25
×(
)=
×
2
4
3、
先找出每组数中各数的倒数,再看看能发现什么
?
我的发现
⑴
真分数的倒数一定大于
1
。
我的发现
4
3
5
2
9
7
先找出每组数中各数的倒数,再看看能发现什么
?
大于
1
的假分数的倒数一定小于
1
。
⑵
我的发现
2
7
5
9
6
13
先找出每组数中各数的倒数,再看看能发现什么
?
⑶
分子是1的分数的倒数一定是整数
。
我的发现
2
10
12
先找出每组数中各数的倒数,再看看能发现什么
?
⑴
真分数的倒数一定大于
1
。
大于
1
的假分数的倒数一定小于
1
。
整数(0除外)的倒数的分子一定是
1
。
⑵
⑷
⑶
分子是1的分数的倒数一定是整数
。
我的发现
先找出每组数中各数的倒数,再看看能发现什么
?
训练发展
1.
乘积是1
的
两个数
叫做
互为
倒数。
乘积是1
两个数
互为
2.
求一个数
的倒数,只要把这个数的分子、分母调换位置。
(0除外)
4.
求整数的倒数,先把整数看成分母是1的分数,再分子、分母调换位置。
3.
0没有倒数,1的倒数是它本身1。
5.
求小数的倒数,先把小数化成分数,再分子、分母调换位置。
训练发展
7.
真分数的倒数一定大于1;
大于1的假分数的倒数一定小于1;
分子是1的分数,它的倒数一定是整数;
不为0的整数,它的倒数的分子一定是1。
6.
求带分数的倒数,先把带分数化成假分数,再分子、分母调换位置。
1、
的倒数的
是多少?
2、最大的两位数与最小的两位数的和的倒数是多少?
总结:今天我们学习了什么知识?你有什么收获?还有什么问题吗?
