七年级数学有理数总复习(实用)
文档属性
| 名称 | 七年级数学有理数总复习(实用) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-06-28 09:15:45 | ||
图片预览










文档简介
(共62张PPT)
重温这些知识,你会觉得亲切!
祝你周末愉快!
1.负数 2.有理数 3.数轴
4.互为相反数
5.互为倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法、近似数与有效数字
一、有理数的基本概念
二、有理数的运算
加、减、乘、除、乘方运算
一、有理数的基本概念
1.负数:
在正数前面加“—”的数;
0既不是正数,也不是负数。
判断:
1)a一定是正数;
2)-a一定是负数;
3)-(-a)一定大于0;
4)0表示没有。
×
×
×
×
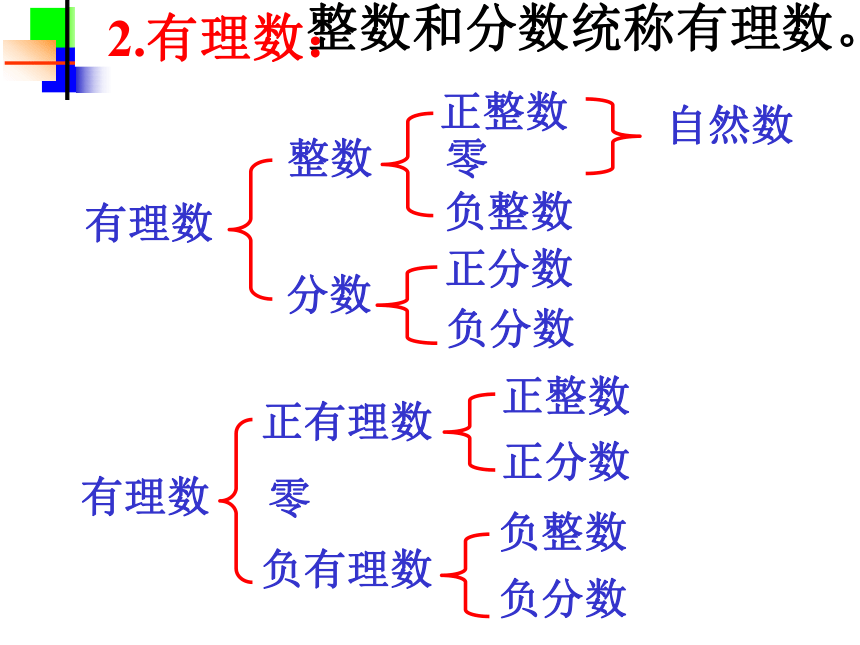
2.有理数:
整数和分数统称有理数。
有理数
整数
分数
正整数
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
自然数
零
非负整数集有
12,0,︱-8︱
[基础练习]
1☆把下列各数填在相应额大括号内:
1,-0.1,-789,25,0,-20,-3.14,-590,6/7
·正整数集{ …}; ·正有理数集{ …};
·负有理数集{ …};·负整数集{ …};
·自然数集{ …}; ·正分数集{ …}
·负分数集{ …}
2☆ 某种食用油的价格随着市场经济的变化涨落,规定上涨记为正,则-5.8元的意义是 ;如果这种油的原价是76元,那么现在的卖价是 。
3.数 轴
规定了原点、正方向和单位长度的直线.
1)在数轴上表示的两个数,
右边的数总比左边的数大;
2)正数都大于0,负数都小于0;
正数大于一切负数;
-3 –2 –1 0 1 2 3 4
3)所有有理数都可以用数轴上
的点表示。
[练习]
★ ①比-3大的负整数是_______; ②已知m是整数且-4-2,-1
-3,-2,-1,0,1,2
-1
1
0
+3
-3
2
★ ★选择题:
(1)在数轴上,原点及原点左边所表示的数( )
A整数 B负数 C非负数 D非正数
(2)下列语句中正确的是( ) A数轴上的点只能表示整数
B数轴上的点只能表示分数
C数轴上的点只能表示有理数
D所有有理数都可以用数轴上的点表示出来
(3)在数轴上点A表示-4,如果把原点O向负方向移
动1个单位,那么在新数轴上点A表示的数是( )
A.-5, B.-4 C.-3 D.-2
D
D
C
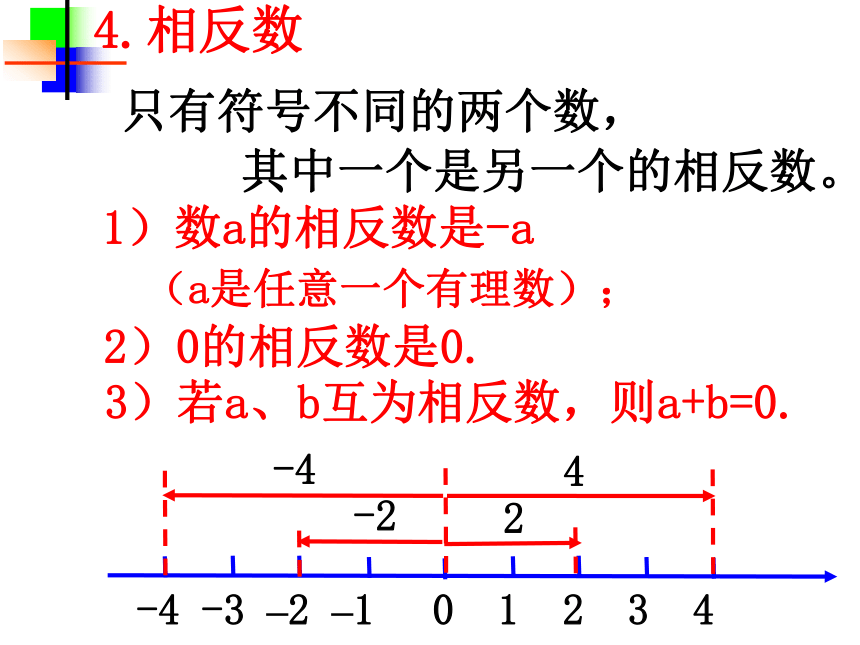
4.相反数
只有符号不同的两个数,
其中一个是另一个的相反数。
1)数a的相反数是-a
2)0的相反数是0.
-4 -3 –2 –1 0 1 2 3 4
-2
2
-4
4
3)若a、b互为相反数,则a+b=0.
(a是任意一个有理数);
[基础练习]
1☆-5的相反数是 ;-(-8)的相反数是 ;
- [+(-6)]=________;0的相反数是 ; a的相反数是 ; 的相反数的倒数是______________ ;
2☆若a和b是互为相反数,则a+b=( )
A. –2a B .2b C. 0 D. 任意有理数
3★(1)如果a=-13,那么-a=______;
(2)如果-a=-5.4,那么a=______;
(3)如果-x=-6,那么x=______;
(4)-x=9,那么x=______.
4★★已知a、b都是有理数,且|a|=a,|b|=-b,则ab是( )
A.负数; B.正数; C.负数或零; D.非负数
5
-8
6
0
-a
8
C
13
5.4
6
-9
C
5、用-a表示的数一定是( )
A .负数 B. 正数
C .正数或负数 D.正数或负数或0
6、一个数的相反数是最小的正整数,那么这个数是( )
A .–1 B. 1 C .±1 D. 0
7、①互为相反的两个数在数轴上位于原点两旁( )
②在一个数前面添上“-”号,它就成了一个负数( )
③ 只要符号不同,这两个数就是相反数( )
D
A
×
×
×
5.倒 数
乘积是1的两个数互为倒数.
1)a的倒数是 (a≠0);
3)若a与b互为倒数,则ab=1.
2)0没有倒数 ;
下列各数,哪两个数互为倒数?
8, ,-1,+(-8),1,
4)倒数是它本身的是______.
6.绝对值
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
1)数a的绝对值记作︱a︱;
若a>0,则︱a︱= ;
2) 若a<0,则︱a︱= ;
若a =0,则︱a︱= ;
-3 –2 –1 0 1 2 3 4
2
3
4
a
-a
0
3) 对任何有理数a,总有︱a︱≥0.
[基础练习]
1☆—2的绝对值表示它离开原点的距离是 个单位,记作 .
2☆ |-8|= ; -|-5|= ; 绝对值等于4的数是__________。
3☆绝对值等于其相反数的数一定是( ) A.负数 B.正数
C.负数或零 D.正数或零
4★ ,则x=______; , 则 x=_______;
2
︱-2︱
8
-5
±4
C
±7
±7
5★★如果 ,则
.
6★★绝对值不大于11的整数有( )
A.11个 B.12个
C.22个 D.23个
a-3
3-a
D
例:在数轴上表示绝对值不小于2而又不大于5.1的所有整数;并求出绝对值小于4的所有整数的和与积
-5
4
3
2
5
-2
-3
-4
绝对值小于4的所有整数的和:
绝对值小于4的所有整数的积:
(-3)+(-2)+(-1)+1+2+3+0= 0
0
(-3)×(-2)×(-1)×0 × 1×2×3= 0
1)绝对值小于2的整数有________。
2)绝对值等于它本身的数有___________。
3)绝对值不大于3的负整数有__________。
4)数a和b的绝对值分别为2和5,且在数轴上
表示a的点在表示b的点左侧,则b的值为 .
0,±1
零和正数
-1,-2,-3
5
练习2
1、若(x-1)2+|y+4|=0,则3x+5y=______
∵X-1=0,y+4=0, ∴x=1 ,y=-4
∴3x+5y=3×1+5×(-4)=3-20=-17
2、若|a-3|+ |3a-4b|=0,则-2a+8b=____
3、| 7 |=( ),|- 7 |=( )
绝对值是7的数是( )
4、若|3- |+|4- |=_______
±7
7
7
1
12
5、已知|x|=3,|y|=2,且x∵|x|=3,|y|=2
∴x=±3,y=±2
∵ x∴x不能为3
∴x=-3,y=2 或 x=-3,y=-2
∴x+y=-3+2=-1 或 x+y=-3-2=-5
-1或-5
6、计算
先去掉绝对值符号,再进行计算!
答案:9/10
7.有理数大小的比较
1)可通过数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数;
2)两个负数,绝对值大的反而小。
即:若a<0,b<0,且︱a︱>︱b︱,
则a < b.
8.科学记数法、近似数与有效数字
1. 把一个大于10的数记成a×10n
的形式,其中a是整数数位只有一位
的数,这种记数法叫做科学记数法 .
2. 一个近似数,从左边第一个不是0
的数字起到,到精确到的数位止,所
有的数字,都叫做这个数的有效数字。
一只苍蝇的腹内细菌多达2800万个,
你能用科学记数法表示吗
2800万个=2.8×103(万个)
或 2800万个=28 000 000个=2.8×107个
1.03×106有几位整数
3.0×10n(n是正整数)有几位整数?
(n+1位整数)
(1 030 000)
(有7位整数)
例:下列由四舍五入得到的近似数,各精确到哪一位,各有几位有效数字?
(1)43.8(2)0.03086(3)2.4万
(4)6×104 (5)6.0×104
解:
(1)43.8精确到十分位.有3个有效数字:4,3,8;
(2)0.03086精确到十万分位,有四个有效数字:3,0,8,6;
(3)2.4万精确到千位,有2个有效数字:2,4;
(4) 6×104 精确到万位,有1个有效数字:6 ;
(5) 6.0×104 精确到千位,有2个有效数字:6 ,0;
[基础练习]
1☆用科学记数数表示:
①1305000000= ;
②-1020= .
2★4万的原数是 .
3★. 近似数3.5万精确到 位,
有 个有效数字.
4★近似数0.4062精确到 ,
有 个有效数字.
1.305×109
-1.02×103
40000
千
2
万分位
4
有理数的五种运算
1.运算法则
2.运算顺序
3.运 算 律
1.运算法则
1)有理数加法法则
2)有理数减法法则
3)有理数乘法法则
4)有理数除法法则
5)有理数的乘方
1)有理数加法法则
① 同号两数相加,取相同的符号,并把绝对值相加;
② 异号两数相加,取绝对值较大
的加数的符号,并用较大的绝对值
减去较小的绝对值;互为相反数
的两数相加得0;
③ 一个数同0相加,仍得这个数。
有理数加法法则应用举例:
①同号相加:
②异号相加
③与0相加
若a、b互为相反数,则a+b=
a是任一个有理数,则a+0=
0
a
(-5)+(-3)=-8
(+5)+(+3)=8
5+(-3)= 2
-5+(+3)= -2
2)有理数减法法则
减去一个数,等于加上这个数的相反数.
即 a-b=a+(-b)
例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。
解:①2-(-7)=2+7=9
(或︱-7-2︱=︱-9︱=9)
②-1-(-3)=-1+3=2
3)有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0.
① 几个不等于0的数相乘,积的符号
由负因数的个数决定,当负因数有奇
数个时,积为负;当负因数有偶数个
时,积为正.
② 几个数相乘,有一个因数为0,
积就为0.
①同号相乘
②异号相乘
③数与0相乘
a为任何有理数,则 a×0=
0
有理数乘法法则应用举例:
2×3=6
(-2)×3 = -6
(-2)×(-3)=6
2×(-3)= -6
④连乘
(-2)×(-3)×(-4) =-24
(-2)×3×(-4) =24
4)有理数除法法则
①除以一个数等于乘上这个数的倒数;
即
a÷b=a× (b≠0)
② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都
得0.
5)有理数的乘方
①求n个相同因数的积的运算,叫做乘方。
②正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数.
幂
指数
底数
即a·a·a· ··· ·a=
n 个
练习
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,
指数是 ,读作 ;
7
的7次方
底
指
12的10次方
12的10次幂
9、计算: 42+(-27)+27+58
解: 原式=〔(-27)+27〕+(58 +42)
小试牛刀
=0+100
=100
10、计算:
解: 原式=
=8+6-4 =10
小试牛刀
11、计算:
(1)-32= (2)(-3)2= (3)-33= (4)(-3)3=
-9
小试牛刀
9
-27
-27
11、计算:
(5)-(-3)2= (6)- (-2)3=
-9
(7) (8)
-(- 8)=8
小试牛刀
12、计算:
-14+(-2)2-23-(-2)3
解:原式=-1+4-8-(-8)
小试牛刀
= -1+4-8+8
= 3
13、计算:
- 32÷(- 3)2+3×(- 6)
解:原式=-9 ÷9+(-18)
小试牛刀
= -1+(-18)
= -19
1、计算:-1.2+3-4-0.8= 。
2、某运动员在东西走向的公路上练习跑步,跑步情况记录如下:(向东为正,单位:米)
1000,-1200,1100,-800,1400
该运动员共跑的路程为( )
A.1500米 B.5500米 C.4500米 D.3700米
丰收园
-3
B
丰收园
3、五个有理数的积为负数,则五个数中负数的个数是( )
A.1 B.3 C.5 D.1或3或5
4、一个数的立方等于它本身,这个数是( )
A.0 B.1
C.-1,1 D.-1,1,0
D
D
5、一杯饮料,第一次喝了一半,第二次喝了剩下的一半,…如此喝下去,第五次喝后剩下的饮料是原来的几分之几?
丰收园
丰收园
6、五袋白糖以每袋50千克为标准,超过的记为正,不足的记为负,称量记录如下:
+4.5,-4,+2.3,-3.5,+2.5
(1)这五袋白糖共超过多少千克?
(2)总重量是多少千克?
解:(1)+4.5-4+2.3-3.5+2.5=1.8
(2)50×5+1.8=251.8
丰收园
7、在下列说法中,正确的个数是( )
⑴任何一个有理数都可以用数轴上的一个点来表示
⑵数轴上的每一个点都表示一个有理数
⑶任何有理数的绝对值都不可能是负数
⑷每个有理数都有相反数
A、4 B、3 C、2 D、1
B
丰收园
8、下列说法正确的是( )
A、正数与负数统称为有理数
B、带负号的数是负数
C、正数一定大于0
D、最大的负数是-1
C
丰收园
9、在数轴上,原点两旁与原点等距离的两点所表示的数的关系是( )
A、相等 B、互为相反数
C、互为倒数 D、不能确定
10、如果一个数的相反数比它本身大,
那么这个数为( )
A、正数 B、负数
C、非负数 D、不等于零的有理数
B
B
丰收园
11、在有理数中,倒数等于本身的数有( )
A、1个 B、2个 C、3个 D、无数个
B
下面的解题过程是否正确?如果有错误请加以订正。
改正:
3.有理数的运算律
1)加法交换律
a+b=b+a
2)加法结合律
(a+b)+c=a+(b+c)
3)乘法交换律
ab=ba
4)乘法结合律
(ab)c=a(bc)
5)分 配 律
a(b+c)=ab+ac
解 题 技 能
加法四结合
1.凑整结合法 2.同号结合法
3.两个相反数结合法
4.同分母或易通分的分数结合法
A、5.6+(-0.9)+4.4+(-8.1)+(-1)
C、(+7)-(-15)+(-12)-(+7)
D、1-4+7-10+13-16+19-22
解 题 技 能
乘法三结合
1、积为整数结合
2、两个倒数结合
3、能约分的结合
分配律
分配律反着用
73、
分配律计算技巧
真假分配律
专题训练1 充分利用概念
互为相反数的两个数的和为0,互为倒数的积为1.绝对值是正数的有两个,且它们互为相反数
例:已知a、b互为相反数,c,d互为倒数,m是绝对值最小的数,求代数式
非负数性质的应用
数形结合的思想方法
已知︱a︱>︱b︱,且a<0,b>0,试比较a,b,-a,-b的大小
分类讨论的思想
比较1+a与1-a的大小。
练习
1、已知有理数a、b、c在数轴上的位置如图,化简|a|-|a+b|+|c-a|+|b+c||
b
a
0
c
拆项、合并法在计算中的应用
1、若a>0,b<0,且|a|<|b|,则a+b___0
特殊值法
2、若x<0,y>0,且|x|<|y|,则x+y__0
重温这些知识,你会觉得亲切!
祝你周末愉快!
1.负数 2.有理数 3.数轴
4.互为相反数
5.互为倒数
6.有理数的绝对值
7.有理数大小的比较
8.科学记数法、近似数与有效数字
一、有理数的基本概念
二、有理数的运算
加、减、乘、除、乘方运算
一、有理数的基本概念
1.负数:
在正数前面加“—”的数;
0既不是正数,也不是负数。
判断:
1)a一定是正数;
2)-a一定是负数;
3)-(-a)一定大于0;
4)0表示没有。
×
×
×
×
2.有理数:
整数和分数统称有理数。
有理数
整数
分数
正整数
负整数
正分数
负分数
有理数
正有理数
零
负有理数
正整数
正分数
负整数
负分数
自然数
零
非负整数集有
12,0,︱-8︱
[基础练习]
1☆把下列各数填在相应额大括号内:
1,-0.1,-789,25,0,-20,-3.14,-590,6/7
·正整数集{ …}; ·正有理数集{ …};
·负有理数集{ …};·负整数集{ …};
·自然数集{ …}; ·正分数集{ …}
·负分数集{ …}
2☆ 某种食用油的价格随着市场经济的变化涨落,规定上涨记为正,则-5.8元的意义是 ;如果这种油的原价是76元,那么现在的卖价是 。
3.数 轴
规定了原点、正方向和单位长度的直线.
1)在数轴上表示的两个数,
右边的数总比左边的数大;
2)正数都大于0,负数都小于0;
正数大于一切负数;
-3 –2 –1 0 1 2 3 4
3)所有有理数都可以用数轴上
的点表示。
[练习]
★ ①比-3大的负整数是_______; ②已知m是整数且-4
-3,-2,-1,0,1,2
-1
1
0
+3
-3
2
★ ★选择题:
(1)在数轴上,原点及原点左边所表示的数( )
A整数 B负数 C非负数 D非正数
(2)下列语句中正确的是( ) A数轴上的点只能表示整数
B数轴上的点只能表示分数
C数轴上的点只能表示有理数
D所有有理数都可以用数轴上的点表示出来
(3)在数轴上点A表示-4,如果把原点O向负方向移
动1个单位,那么在新数轴上点A表示的数是( )
A.-5, B.-4 C.-3 D.-2
D
D
C
4.相反数
只有符号不同的两个数,
其中一个是另一个的相反数。
1)数a的相反数是-a
2)0的相反数是0.
-4 -3 –2 –1 0 1 2 3 4
-2
2
-4
4
3)若a、b互为相反数,则a+b=0.
(a是任意一个有理数);
[基础练习]
1☆-5的相反数是 ;-(-8)的相反数是 ;
- [+(-6)]=________;0的相反数是 ; a的相反数是 ; 的相反数的倒数是______________ ;
2☆若a和b是互为相反数,则a+b=( )
A. –2a B .2b C. 0 D. 任意有理数
3★(1)如果a=-13,那么-a=______;
(2)如果-a=-5.4,那么a=______;
(3)如果-x=-6,那么x=______;
(4)-x=9,那么x=______.
4★★已知a、b都是有理数,且|a|=a,|b|=-b,则ab是( )
A.负数; B.正数; C.负数或零; D.非负数
5
-8
6
0
-a
8
C
13
5.4
6
-9
C
5、用-a表示的数一定是( )
A .负数 B. 正数
C .正数或负数 D.正数或负数或0
6、一个数的相反数是最小的正整数,那么这个数是( )
A .–1 B. 1 C .±1 D. 0
7、①互为相反的两个数在数轴上位于原点两旁( )
②在一个数前面添上“-”号,它就成了一个负数( )
③ 只要符号不同,这两个数就是相反数( )
D
A
×
×
×
5.倒 数
乘积是1的两个数互为倒数.
1)a的倒数是 (a≠0);
3)若a与b互为倒数,则ab=1.
2)0没有倒数 ;
下列各数,哪两个数互为倒数?
8, ,-1,+(-8),1,
4)倒数是它本身的是______.
6.绝对值
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
1)数a的绝对值记作︱a︱;
若a>0,则︱a︱= ;
2) 若a<0,则︱a︱= ;
若a =0,则︱a︱= ;
-3 –2 –1 0 1 2 3 4
2
3
4
a
-a
0
3) 对任何有理数a,总有︱a︱≥0.
[基础练习]
1☆—2的绝对值表示它离开原点的距离是 个单位,记作 .
2☆ |-8|= ; -|-5|= ; 绝对值等于4的数是__________。
3☆绝对值等于其相反数的数一定是( ) A.负数 B.正数
C.负数或零 D.正数或零
4★ ,则x=______; , 则 x=_______;
2
︱-2︱
8
-5
±4
C
±7
±7
5★★如果 ,则
.
6★★绝对值不大于11的整数有( )
A.11个 B.12个
C.22个 D.23个
a-3
3-a
D
例:在数轴上表示绝对值不小于2而又不大于5.1的所有整数;并求出绝对值小于4的所有整数的和与积
-5
4
3
2
5
-2
-3
-4
绝对值小于4的所有整数的和:
绝对值小于4的所有整数的积:
(-3)+(-2)+(-1)+1+2+3+0= 0
0
(-3)×(-2)×(-1)×0 × 1×2×3= 0
1)绝对值小于2的整数有________。
2)绝对值等于它本身的数有___________。
3)绝对值不大于3的负整数有__________。
4)数a和b的绝对值分别为2和5,且在数轴上
表示a的点在表示b的点左侧,则b的值为 .
0,±1
零和正数
-1,-2,-3
5
练习2
1、若(x-1)2+|y+4|=0,则3x+5y=______
∵X-1=0,y+4=0, ∴x=1 ,y=-4
∴3x+5y=3×1+5×(-4)=3-20=-17
2、若|a-3|+ |3a-4b|=0,则-2a+8b=____
3、| 7 |=( ),|- 7 |=( )
绝对值是7的数是( )
4、若|3- |+|4- |=_______
±7
7
7
1
12
5、已知|x|=3,|y|=2,且x
∴x=±3,y=±2
∵ x
∴x=-3,y=2 或 x=-3,y=-2
∴x+y=-3+2=-1 或 x+y=-3-2=-5
-1或-5
6、计算
先去掉绝对值符号,再进行计算!
答案:9/10
7.有理数大小的比较
1)可通过数轴比较:
在数轴上的两个数,右边的数
总比左边的数大;
正数都大于0,负数都小于0;
正数大于一切负数;
2)两个负数,绝对值大的反而小。
即:若a<0,b<0,且︱a︱>︱b︱,
则a < b.
8.科学记数法、近似数与有效数字
1. 把一个大于10的数记成a×10n
的形式,其中a是整数数位只有一位
的数,这种记数法叫做科学记数法 .
2. 一个近似数,从左边第一个不是0
的数字起到,到精确到的数位止,所
有的数字,都叫做这个数的有效数字。
一只苍蝇的腹内细菌多达2800万个,
你能用科学记数法表示吗
2800万个=2.8×103(万个)
或 2800万个=28 000 000个=2.8×107个
1.03×106有几位整数
3.0×10n(n是正整数)有几位整数?
(n+1位整数)
(1 030 000)
(有7位整数)
例:下列由四舍五入得到的近似数,各精确到哪一位,各有几位有效数字?
(1)43.8(2)0.03086(3)2.4万
(4)6×104 (5)6.0×104
解:
(1)43.8精确到十分位.有3个有效数字:4,3,8;
(2)0.03086精确到十万分位,有四个有效数字:3,0,8,6;
(3)2.4万精确到千位,有2个有效数字:2,4;
(4) 6×104 精确到万位,有1个有效数字:6 ;
(5) 6.0×104 精确到千位,有2个有效数字:6 ,0;
[基础练习]
1☆用科学记数数表示:
①1305000000= ;
②-1020= .
2★4万的原数是 .
3★. 近似数3.5万精确到 位,
有 个有效数字.
4★近似数0.4062精确到 ,
有 个有效数字.
1.305×109
-1.02×103
40000
千
2
万分位
4
有理数的五种运算
1.运算法则
2.运算顺序
3.运 算 律
1.运算法则
1)有理数加法法则
2)有理数减法法则
3)有理数乘法法则
4)有理数除法法则
5)有理数的乘方
1)有理数加法法则
① 同号两数相加,取相同的符号,并把绝对值相加;
② 异号两数相加,取绝对值较大
的加数的符号,并用较大的绝对值
减去较小的绝对值;互为相反数
的两数相加得0;
③ 一个数同0相加,仍得这个数。
有理数加法法则应用举例:
①同号相加:
②异号相加
③与0相加
若a、b互为相反数,则a+b=
a是任一个有理数,则a+0=
0
a
(-5)+(-3)=-8
(+5)+(+3)=8
5+(-3)= 2
-5+(+3)= -2
2)有理数减法法则
减去一个数,等于加上这个数的相反数.
即 a-b=a+(-b)
例:分别求出数轴上两点间的距离:
①表示2的点与表示-7的点;
②表示-3的点与表示-1的点。
解:①2-(-7)=2+7=9
(或︱-7-2︱=︱-9︱=9)
②-1-(-3)=-1+3=2
3)有理数的乘法法则
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0.
① 几个不等于0的数相乘,积的符号
由负因数的个数决定,当负因数有奇
数个时,积为负;当负因数有偶数个
时,积为正.
② 几个数相乘,有一个因数为0,
积就为0.
①同号相乘
②异号相乘
③数与0相乘
a为任何有理数,则 a×0=
0
有理数乘法法则应用举例:
2×3=6
(-2)×3 = -6
(-2)×(-3)=6
2×(-3)= -6
④连乘
(-2)×(-3)×(-4) =-24
(-2)×3×(-4) =24
4)有理数除法法则
①除以一个数等于乘上这个数的倒数;
即
a÷b=a× (b≠0)
② 两数相除,同号得正,异号得负,
并把绝对值相除;
0除以任何一个不等于0的数,都
得0.
5)有理数的乘方
①求n个相同因数的积的运算,叫做乘方。
②正数的任何次幂都是正数;
负数的奇次幂是负数,
负数的偶次幂是正数.
幂
指数
底数
即a·a·a· ··· ·a=
n 个
练习
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,
指数是 ,读作 ;
7
的7次方
底
指
12的10次方
12的10次幂
9、计算: 42+(-27)+27+58
解: 原式=〔(-27)+27〕+(58 +42)
小试牛刀
=0+100
=100
10、计算:
解: 原式=
=8+6-4 =10
小试牛刀
11、计算:
(1)-32= (2)(-3)2= (3)-33= (4)(-3)3=
-9
小试牛刀
9
-27
-27
11、计算:
(5)-(-3)2= (6)- (-2)3=
-9
(7) (8)
-(- 8)=8
小试牛刀
12、计算:
-14+(-2)2-23-(-2)3
解:原式=-1+4-8-(-8)
小试牛刀
= -1+4-8+8
= 3
13、计算:
- 32÷(- 3)2+3×(- 6)
解:原式=-9 ÷9+(-18)
小试牛刀
= -1+(-18)
= -19
1、计算:-1.2+3-4-0.8= 。
2、某运动员在东西走向的公路上练习跑步,跑步情况记录如下:(向东为正,单位:米)
1000,-1200,1100,-800,1400
该运动员共跑的路程为( )
A.1500米 B.5500米 C.4500米 D.3700米
丰收园
-3
B
丰收园
3、五个有理数的积为负数,则五个数中负数的个数是( )
A.1 B.3 C.5 D.1或3或5
4、一个数的立方等于它本身,这个数是( )
A.0 B.1
C.-1,1 D.-1,1,0
D
D
5、一杯饮料,第一次喝了一半,第二次喝了剩下的一半,…如此喝下去,第五次喝后剩下的饮料是原来的几分之几?
丰收园
丰收园
6、五袋白糖以每袋50千克为标准,超过的记为正,不足的记为负,称量记录如下:
+4.5,-4,+2.3,-3.5,+2.5
(1)这五袋白糖共超过多少千克?
(2)总重量是多少千克?
解:(1)+4.5-4+2.3-3.5+2.5=1.8
(2)50×5+1.8=251.8
丰收园
7、在下列说法中,正确的个数是( )
⑴任何一个有理数都可以用数轴上的一个点来表示
⑵数轴上的每一个点都表示一个有理数
⑶任何有理数的绝对值都不可能是负数
⑷每个有理数都有相反数
A、4 B、3 C、2 D、1
B
丰收园
8、下列说法正确的是( )
A、正数与负数统称为有理数
B、带负号的数是负数
C、正数一定大于0
D、最大的负数是-1
C
丰收园
9、在数轴上,原点两旁与原点等距离的两点所表示的数的关系是( )
A、相等 B、互为相反数
C、互为倒数 D、不能确定
10、如果一个数的相反数比它本身大,
那么这个数为( )
A、正数 B、负数
C、非负数 D、不等于零的有理数
B
B
丰收园
11、在有理数中,倒数等于本身的数有( )
A、1个 B、2个 C、3个 D、无数个
B
下面的解题过程是否正确?如果有错误请加以订正。
改正:
3.有理数的运算律
1)加法交换律
a+b=b+a
2)加法结合律
(a+b)+c=a+(b+c)
3)乘法交换律
ab=ba
4)乘法结合律
(ab)c=a(bc)
5)分 配 律
a(b+c)=ab+ac
解 题 技 能
加法四结合
1.凑整结合法 2.同号结合法
3.两个相反数结合法
4.同分母或易通分的分数结合法
A、5.6+(-0.9)+4.4+(-8.1)+(-1)
C、(+7)-(-15)+(-12)-(+7)
D、1-4+7-10+13-16+19-22
解 题 技 能
乘法三结合
1、积为整数结合
2、两个倒数结合
3、能约分的结合
分配律
分配律反着用
73、
分配律计算技巧
真假分配律
专题训练1 充分利用概念
互为相反数的两个数的和为0,互为倒数的积为1.绝对值是正数的有两个,且它们互为相反数
例:已知a、b互为相反数,c,d互为倒数,m是绝对值最小的数,求代数式
非负数性质的应用
数形结合的思想方法
已知︱a︱>︱b︱,且a<0,b>0,试比较a,b,-a,-b的大小
分类讨论的思想
比较1+a与1-a的大小。
练习
1、已知有理数a、b、c在数轴上的位置如图,化简|a|-|a+b|+|c-a|+|b+c||
b
a
0
c
拆项、合并法在计算中的应用
1、若a>0,b<0,且|a|<|b|,则a+b___0
特殊值法
2、若x<0,y>0,且|x|<|y|,则x+y__0
