第三章 二次函数单元测试题(含答案)
图片预览




文档简介
中小学教育资源及组卷应用平台
《第三章
二次函数》单元测试题
(时间:60分钟
满分:100分)
一、选择题(每小题3分,共24分)
1.函数的自变量的取值范围是(
)
A.x≥-1
B.x≥-1且x≠0
C.x>0
D.x>-1且x≠0
2.给出下列函数:①y=-3x+2;②y=,③y=2x2;④y=3x,上述函数中符合条件“当x>1时,函数值y随自变量x增大而增大”的是(
)
A.①③
B.③④
C.②④
D.②③
3.抛物线y=2(x+3)2+4的顶点坐标是(
)
A.(3,4)
B.(-3,4)
C.(3,-4)
D.(2,4)
4.在平面直角坐标系中,抛物线y=(x+5)(x-3)经变换后得到抛物线y=(x+3)(x-5),则这个变换可以是(
)
A.向左平移2个单位
B.向右平移2个单位
C.向左平移8个单位
D.向右平移8个单位
5.若函数y=ax2+bx+c(a≠0)的图象如图所示,则函数y=ax+b和y=在同一平面直角坐标系中的图象大致是(
)
6.竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0.表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5
m的高处以20
m/s的速度竖直向上抛出,小球达到的离地面的最大高度为(
)
A.23.5
m
B.22.5
m
C.21.5
m
D.20.5
m
7.如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A(-1,0),B(3,0)两点,与y轴的正半轴交于点C,顶点为D,则下列结论:①2a+b=0;②2c<3b;③当△ABC是等腰三角形时,a的值有2个;④当△BCD是直角三角形时,a=.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
8.边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是(
)
二、填空题(每小题4分,共24分)
9.下列y关于x的函数:①y=;②y=-3x2+5;③y=(x-2)2-x2;④y=x3-3x;⑤;⑥y=(k2+1)x2-5.其中是二次函数的有____________.(只填序号)
10.二次函数y=ax2+bx+c的部分对应值如下表:
x
-3
-2
-1
0
1
2
3
4
5
y
12
5
0
-3
-4
-3
0
5
12
利用二次函数的图象可知,当函数值y>0时,x的取值范围是____________.
11.如图所示,在平面直角坐标系xOy中,已知抛物线y=ax2+bx(a>0)的顶点为C,与x轴的正半轴交于点A,它的对称轴与抛物线y=ax2(a>0)交于点B.若四边形ABOC是正方形,则b的值是__________.
12.若抛物线y=-2(x-h)2+k(h,k为常数)与直线y=3交于A,B两点,A在B的左侧,AB=4,则k的值为__________.
13.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t-t2,在飞机着陆滑行中,最后2s滑行的距离是_________m.
14.如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A,B,顶点为C,对称轴为直线x=1,给出下列结论:①abc<0;②若点C的坐标为(1,2),则△ABC的面积可以等于2;③M(x1,y1),N(x2,y2)是抛物线上两点(x1<x2),若x1+x2>2,则y1<y2;④若抛物线经过点(3,-1),则方程ax2+bx+c+1=0的两根为-1,3.其中正确结论的序号为_____________.
三、解答题(共52分)
15.(6分)如图所示,二次函数y=ax2+bx+c的图象过点A(-1,0),B(3,0)和点C(4,5).
(1)求该二次函数的表达式及最小值;
(2)点P(m,n)是该二次函数图象上一点.
①当m=-4时,求n的值;
②已知点P到y轴的距离不大于4,请根据图象直接写出n的取值范围.
16.(8分)如图①,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积(图②中阴影部分).
17.(8分)某商场以10元/件的价格购进某款智能玩具,销售单价为x(元),在销售过程中发现:当14≤x≤20时,该智能玩具的日销售量y(件)与销售单价x之间存在一次函数关系,x,y之间的部分数值对应关系如下表:
销售单价x(元)
14
20
日销售量y(件)
32
20
(1)请写出当14≤x≤20时,y与x之间的函数关系式;
(2)该智能玩具的销售单价x(元)定为多少时,日销售利润最大?最大利润是多少?
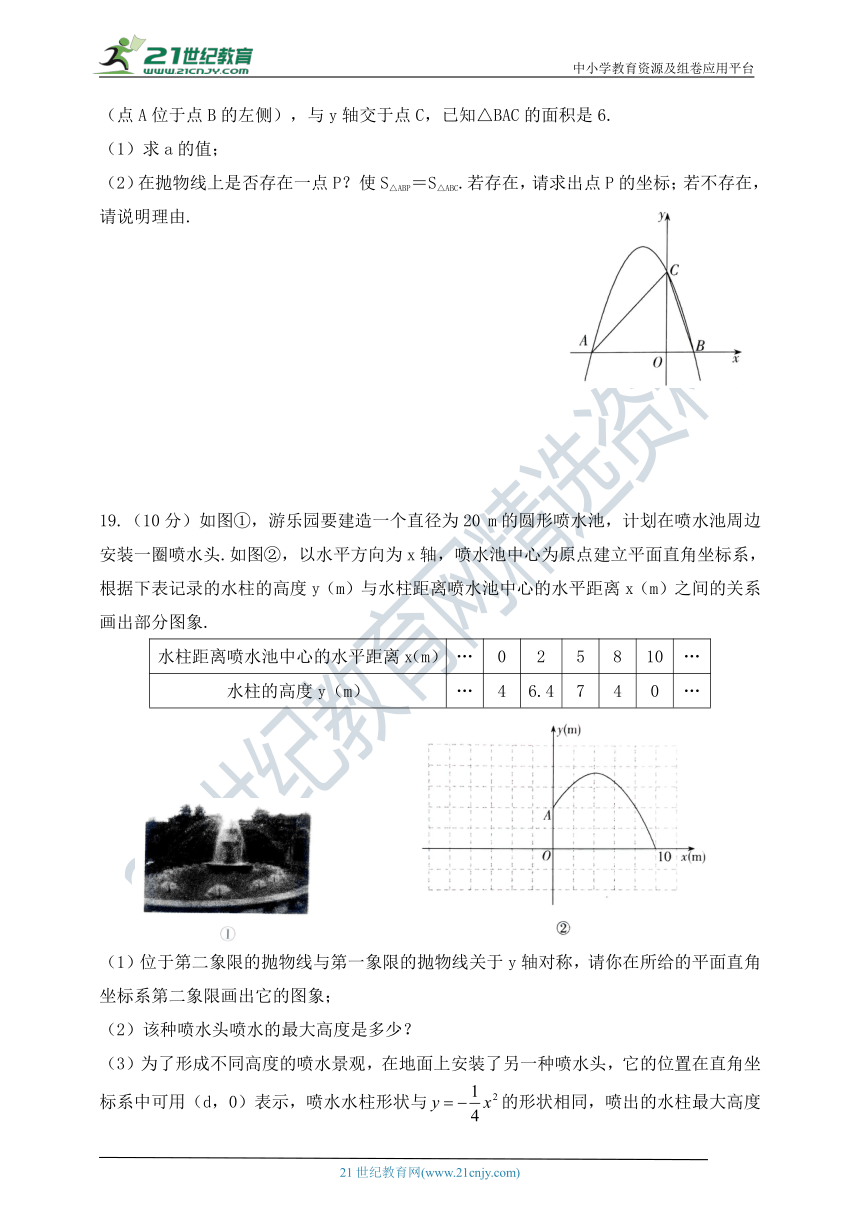
18.(8分)如图所示,已知二次函数y=-x2+(a+1)x-a的图象与x轴交于A,B两点(点A位于点B的左侧),与y轴交于点C,已知△BAC的面积是6.
(1)求a的值;
(2)在抛物线上是否存在一点P?使S△ABP=S△ABC.若存在,请求出点P的坐标;若不存在,请说明理由.
19.(10分)如图①,游乐园要建造一个直径为20
m的圆形喷水池,计划在喷水池周边安装一圈喷水头.如图②,以水平方向为x轴,喷水池中心为原点建立平面直角坐标系,根据下表记录的水柱的高度y(m)与水柱距离喷水池中心的水平距离x(m)之间的关系画出部分图象.
水柱距离喷水池中心的水平距离x(m)
…
0
2
5
8
10
…
水柱的高度y(m)
…
4
6.4
7
4
0
…
(1)位于第二象限的抛物线与第一象限的抛物线关于y轴对称,请你在所给的平面直角坐标系第二象限画出它的图象;
(2)该种喷水头喷水的最大高度是多少?
(3)为了形成不同高度的喷水景观,在地面上安装了另一种喷水头,它的位置在直角坐标系中可用(d,0)表示,喷水水柱形状与的形状相同,喷出的水柱最大高度为6.25
m,水柱下落时也过点(0,4)。求该种喷水头安装的位置(只在x轴正半轴上).
20.(12分)如图所示,已知抛物线经过两点A(-3,0),B(0,3),且其对称轴为直线x=-1.
(1)求此抛物线的解析式:
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
参考答案
一、选择题
1.B
2.B
3.B
4.B
5.B
6.C
7.B
8.C
二、填空题
9.②⑥
10.x<-1或x>3
11.-2
12.11
13.6
14.①④
三、解答题
15.解析
(1)将点A(-1,0),B(3,0)和点C(4,5)代入y=ax2+bx+c,
得,解得,∴二次函数的表达式为y=x2-2x-3.
化为顶点式得y=(x-1)2-4,
∴当x=1时,y取得最小值,此时y=-4.
(2)①当m=-4时,n=16+8-3=21.
②∵y=x2-2x-3=(x-1)2-4,∴抛物线经过点(4,5),(-4,21),∴-4≤n≤21.
16.解析
(1)将点A(0,3),B(3,0),C(4,3)分别代入函数表达式,
得,解得.∴抛物线的函数表达式为y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2.
(3)阴影部分的面积为2。
17.解析
(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据题意,
得,解得.∴y与x之间的函数关系式为y=-2x+60(14≤x≤20).
(2)设该智能玩具的日销售利润为w元,根据题意,
得w=(-2x+60)(x-10)=-2x2+80x-600=-2(x-20)2+200(14≤x≤20).
∴当x=20时,w取得最大值,此时w=200.
∴该智能玩具的销售单价定为20元时,日销售利润最大,最大利润是200元.
18.解析
(1)令y=-x2+(a+1)x-a=0,即-x2+(a+1)x-a=0,
解得x1=a,x2=1.
由题图知a<0,∴A的坐标为(a,0),B的坐标为(1,0).
∵S△ABC=6,∴(1-a)(-a)-6.解得a=-3或a=4(舍去).
(2)∵a=-3,∴点C的坐标为(0,3).
∵S△ABP=S△ABC,∴P点的纵坐标为±3.
把y=3代入y=-x2-2x+3,得-x2-2x+3=3.解得x=0(舍去)或x=-2.
把y=-3代入y=-x2-2x+3,得-x2-2x+3=-3.解得x=-1+或x=-1-。
∴P点的坐标为(-2,3)或(-1+,-3)或(-1-,-3).
19.解析
(1)如图即为所求作的图象.
(2)由题意可知抛物线的对称轴为直线x=4,与x轴的一个交点坐标为(10,0),则与x轴的另一个交点的坐标为(-2,0).
设抛物线的表达式是y=a(x+2)(x-10),把(0,4)代人,得4=a(0+2)(0-10),解得a=-.
∴y=-(x+2)(x-10)=-(x-4)2+7.2,∴该种喷水头喷水的最大高度是7.2m.
(3)喷水水柱形状与y=-x2的形状相同,且下落时也过点(0,4),
∴设第一象限抛物线的表达式是y=-x2+bx+4(b>0).
∵喷出的水柱最大高度为6.25m,
∴=6.25,解得b1=,b2=-(舍去).
∴y=,令y=0,得=0,解得x1=8,x2=-2(舍去).
∴该种喷水头安装的位置是(8,0).
20.解析
(1)抛物线的对称轴是直线x=-1,且经过点4(-3,0),
∴由抛物线的对称性可知抛物线经过点(1,0).
设抛物线的解析式为y=a(x-x1)(x-x2)(a≠0),即y=a(x-1)(x+3).
把B(0,3)代入,得3=-3a,∴a=-1.∴抛物线的解析式为y=-x2-2x+3.
(2)设直线AB的解析式为y=kx+b(k≠0),将A(-3,0),B(0,3)分别代入,得,解得.∴直线AB的解析式为y=x+3.
作PQ⊥x轴于点Q,交直线AB于点M,设P(x,-x2-2x+3),则M(x,x+3),
∴PM=-x2-2x+3-(x+3)=-x2-3x,
∴S=(-x2-3x)×3=.
当x=-时,S最大值=,此时,
∴△PAB的面积的最大值为,此时点P的坐标为.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
《第三章
二次函数》单元测试题
(时间:60分钟
满分:100分)
一、选择题(每小题3分,共24分)
1.函数的自变量的取值范围是(
)
A.x≥-1
B.x≥-1且x≠0
C.x>0
D.x>-1且x≠0
2.给出下列函数:①y=-3x+2;②y=,③y=2x2;④y=3x,上述函数中符合条件“当x>1时,函数值y随自变量x增大而增大”的是(
)
A.①③
B.③④
C.②④
D.②③
3.抛物线y=2(x+3)2+4的顶点坐标是(
)
A.(3,4)
B.(-3,4)
C.(3,-4)
D.(2,4)
4.在平面直角坐标系中,抛物线y=(x+5)(x-3)经变换后得到抛物线y=(x+3)(x-5),则这个变换可以是(
)
A.向左平移2个单位
B.向右平移2个单位
C.向左平移8个单位
D.向右平移8个单位
5.若函数y=ax2+bx+c(a≠0)的图象如图所示,则函数y=ax+b和y=在同一平面直角坐标系中的图象大致是(
)
6.竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0.表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5
m的高处以20
m/s的速度竖直向上抛出,小球达到的离地面的最大高度为(
)
A.23.5
m
B.22.5
m
C.21.5
m
D.20.5
m
7.如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A(-1,0),B(3,0)两点,与y轴的正半轴交于点C,顶点为D,则下列结论:①2a+b=0;②2c<3b;③当△ABC是等腰三角形时,a的值有2个;④当△BCD是直角三角形时,a=.其中正确的有(
)
A.1个
B.2个
C.3个
D.4个
8.边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是(
)
二、填空题(每小题4分,共24分)
9.下列y关于x的函数:①y=;②y=-3x2+5;③y=(x-2)2-x2;④y=x3-3x;⑤;⑥y=(k2+1)x2-5.其中是二次函数的有____________.(只填序号)
10.二次函数y=ax2+bx+c的部分对应值如下表:
x
-3
-2
-1
0
1
2
3
4
5
y
12
5
0
-3
-4
-3
0
5
12
利用二次函数的图象可知,当函数值y>0时,x的取值范围是____________.
11.如图所示,在平面直角坐标系xOy中,已知抛物线y=ax2+bx(a>0)的顶点为C,与x轴的正半轴交于点A,它的对称轴与抛物线y=ax2(a>0)交于点B.若四边形ABOC是正方形,则b的值是__________.
12.若抛物线y=-2(x-h)2+k(h,k为常数)与直线y=3交于A,B两点,A在B的左侧,AB=4,则k的值为__________.
13.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t-t2,在飞机着陆滑行中,最后2s滑行的距离是_________m.
14.如图所示,抛物线y=ax2+bx+c(a≠0)与x轴交于点A,B,顶点为C,对称轴为直线x=1,给出下列结论:①abc<0;②若点C的坐标为(1,2),则△ABC的面积可以等于2;③M(x1,y1),N(x2,y2)是抛物线上两点(x1<x2),若x1+x2>2,则y1<y2;④若抛物线经过点(3,-1),则方程ax2+bx+c+1=0的两根为-1,3.其中正确结论的序号为_____________.
三、解答题(共52分)
15.(6分)如图所示,二次函数y=ax2+bx+c的图象过点A(-1,0),B(3,0)和点C(4,5).
(1)求该二次函数的表达式及最小值;
(2)点P(m,n)是该二次函数图象上一点.
①当m=-4时,求n的值;
②已知点P到y轴的距离不大于4,请根据图象直接写出n的取值范围.
16.(8分)如图①,已知抛物线y=ax2+bx+c经过点A(0,3),B(3,0),C(4,3).
(1)求抛物线的函数表达式;
(2)求抛物线的顶点坐标和对称轴;
(3)把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积(图②中阴影部分).
17.(8分)某商场以10元/件的价格购进某款智能玩具,销售单价为x(元),在销售过程中发现:当14≤x≤20时,该智能玩具的日销售量y(件)与销售单价x之间存在一次函数关系,x,y之间的部分数值对应关系如下表:
销售单价x(元)
14
20
日销售量y(件)
32
20
(1)请写出当14≤x≤20时,y与x之间的函数关系式;
(2)该智能玩具的销售单价x(元)定为多少时,日销售利润最大?最大利润是多少?
18.(8分)如图所示,已知二次函数y=-x2+(a+1)x-a的图象与x轴交于A,B两点(点A位于点B的左侧),与y轴交于点C,已知△BAC的面积是6.
(1)求a的值;
(2)在抛物线上是否存在一点P?使S△ABP=S△ABC.若存在,请求出点P的坐标;若不存在,请说明理由.
19.(10分)如图①,游乐园要建造一个直径为20
m的圆形喷水池,计划在喷水池周边安装一圈喷水头.如图②,以水平方向为x轴,喷水池中心为原点建立平面直角坐标系,根据下表记录的水柱的高度y(m)与水柱距离喷水池中心的水平距离x(m)之间的关系画出部分图象.
水柱距离喷水池中心的水平距离x(m)
…
0
2
5
8
10
…
水柱的高度y(m)
…
4
6.4
7
4
0
…
(1)位于第二象限的抛物线与第一象限的抛物线关于y轴对称,请你在所给的平面直角坐标系第二象限画出它的图象;
(2)该种喷水头喷水的最大高度是多少?
(3)为了形成不同高度的喷水景观,在地面上安装了另一种喷水头,它的位置在直角坐标系中可用(d,0)表示,喷水水柱形状与的形状相同,喷出的水柱最大高度为6.25
m,水柱下落时也过点(0,4)。求该种喷水头安装的位置(只在x轴正半轴上).
20.(12分)如图所示,已知抛物线经过两点A(-3,0),B(0,3),且其对称轴为直线x=-1.
(1)求此抛物线的解析式:
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
参考答案
一、选择题
1.B
2.B
3.B
4.B
5.B
6.C
7.B
8.C
二、填空题
9.②⑥
10.x<-1或x>3
11.-2
12.11
13.6
14.①④
三、解答题
15.解析
(1)将点A(-1,0),B(3,0)和点C(4,5)代入y=ax2+bx+c,
得,解得,∴二次函数的表达式为y=x2-2x-3.
化为顶点式得y=(x-1)2-4,
∴当x=1时,y取得最小值,此时y=-4.
(2)①当m=-4时,n=16+8-3=21.
②∵y=x2-2x-3=(x-1)2-4,∴抛物线经过点(4,5),(-4,21),∴-4≤n≤21.
16.解析
(1)将点A(0,3),B(3,0),C(4,3)分别代入函数表达式,
得,解得.∴抛物线的函数表达式为y=x2-4x+3.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2.
(3)阴影部分的面积为2。
17.解析
(1)设y与x之间的函数关系式为y=kx+b(k≠0),根据题意,
得,解得.∴y与x之间的函数关系式为y=-2x+60(14≤x≤20).
(2)设该智能玩具的日销售利润为w元,根据题意,
得w=(-2x+60)(x-10)=-2x2+80x-600=-2(x-20)2+200(14≤x≤20).
∴当x=20时,w取得最大值,此时w=200.
∴该智能玩具的销售单价定为20元时,日销售利润最大,最大利润是200元.
18.解析
(1)令y=-x2+(a+1)x-a=0,即-x2+(a+1)x-a=0,
解得x1=a,x2=1.
由题图知a<0,∴A的坐标为(a,0),B的坐标为(1,0).
∵S△ABC=6,∴(1-a)(-a)-6.解得a=-3或a=4(舍去).
(2)∵a=-3,∴点C的坐标为(0,3).
∵S△ABP=S△ABC,∴P点的纵坐标为±3.
把y=3代入y=-x2-2x+3,得-x2-2x+3=3.解得x=0(舍去)或x=-2.
把y=-3代入y=-x2-2x+3,得-x2-2x+3=-3.解得x=-1+或x=-1-。
∴P点的坐标为(-2,3)或(-1+,-3)或(-1-,-3).
19.解析
(1)如图即为所求作的图象.
(2)由题意可知抛物线的对称轴为直线x=4,与x轴的一个交点坐标为(10,0),则与x轴的另一个交点的坐标为(-2,0).
设抛物线的表达式是y=a(x+2)(x-10),把(0,4)代人,得4=a(0+2)(0-10),解得a=-.
∴y=-(x+2)(x-10)=-(x-4)2+7.2,∴该种喷水头喷水的最大高度是7.2m.
(3)喷水水柱形状与y=-x2的形状相同,且下落时也过点(0,4),
∴设第一象限抛物线的表达式是y=-x2+bx+4(b>0).
∵喷出的水柱最大高度为6.25m,
∴=6.25,解得b1=,b2=-(舍去).
∴y=,令y=0,得=0,解得x1=8,x2=-2(舍去).
∴该种喷水头安装的位置是(8,0).
20.解析
(1)抛物线的对称轴是直线x=-1,且经过点4(-3,0),
∴由抛物线的对称性可知抛物线经过点(1,0).
设抛物线的解析式为y=a(x-x1)(x-x2)(a≠0),即y=a(x-1)(x+3).
把B(0,3)代入,得3=-3a,∴a=-1.∴抛物线的解析式为y=-x2-2x+3.
(2)设直线AB的解析式为y=kx+b(k≠0),将A(-3,0),B(0,3)分别代入,得,解得.∴直线AB的解析式为y=x+3.
作PQ⊥x轴于点Q,交直线AB于点M,设P(x,-x2-2x+3),则M(x,x+3),
∴PM=-x2-2x+3-(x+3)=-x2-3x,
∴S=(-x2-3x)×3=.
当x=-时,S最大值=,此时,
∴△PAB的面积的最大值为,此时点P的坐标为.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
