2020—2021学年青岛版数学八年级下册第10章一次函数专项提升练习(word版、附答案)
文档属性
| 名称 | 2020—2021学年青岛版数学八年级下册第10章一次函数专项提升练习(word版、附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 00:00:00 | ||
图片预览


文档简介
青岛版数学八年级下一次函数专项提升练习
一、选择题
(2021·深圳市福田区·期末)如图,在平面直角坐标系中,已知一次函数
分别交
轴、
轴与点
,,若点
是坐标轴上的点,且
为等腰三角形,则满足条件的点
有
A.
个
B.
个
C.
个
D.
个
(2020·广东深圳市·模拟)如图,在平面直角坐标系中,直线
与
轴,
轴分别交于点
和点
,直线
与直线
在第一象限交于点
.若
,则
的值为
A.
B.
C.
D.
(2020·专项)一次函数
满足
,且
随
的增大而减小,则此函数的图象不经过
A.第一象限
B.第二象限
C.第三象限
D.第四象限
二、填空题
(2021·上海闵行区·单元测试)当
时,一次函数的图象
不经过原点.
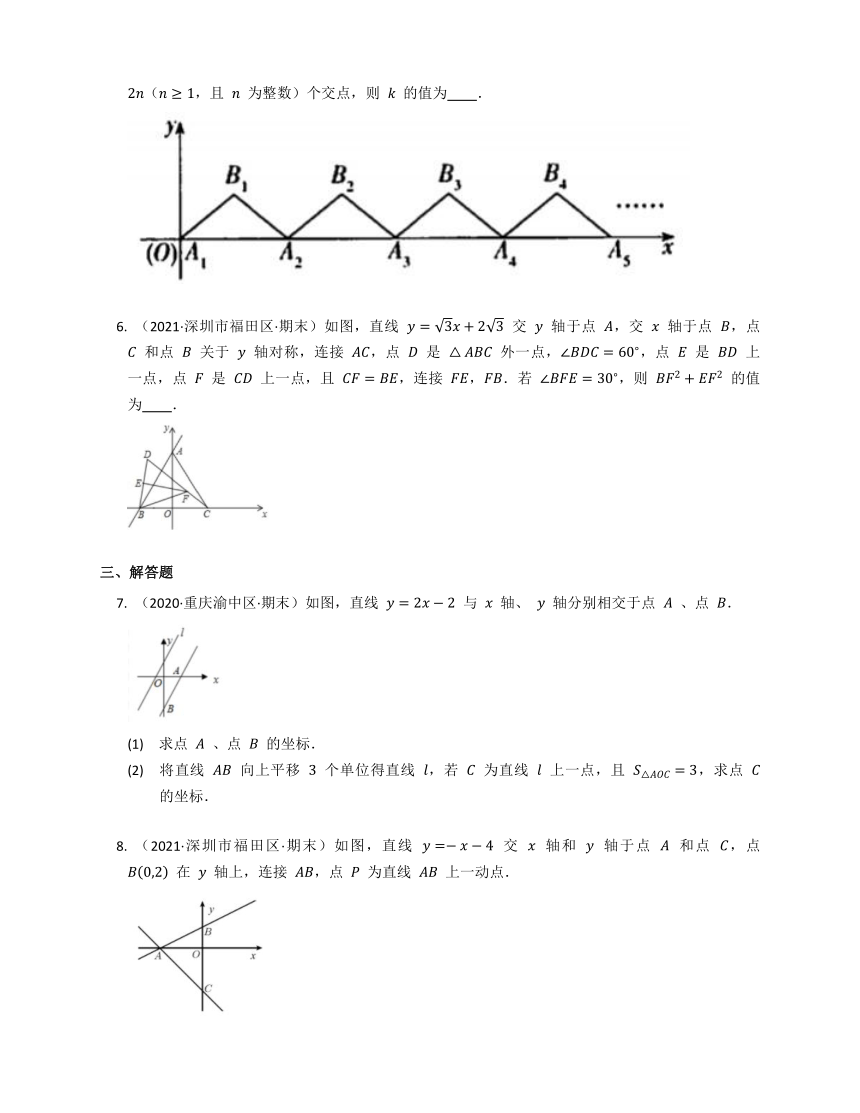
(2021·山东·同步练习)如图,有一条折线
,它是由过
,,
的折线依次平移
,,,
个单位得到的,直线
与此折线恰有
(,且
为整数)个交点,则
的值为
.
(2021·深圳市福田区·期末)如图,直线
交
轴于点
,交
轴于点
,点
和点
关于
轴对称,连接
,点
是
外一点,,点
是
上一点,点
是
上一点,且
,连接
,.若
,则
的值为
.
三、解答题
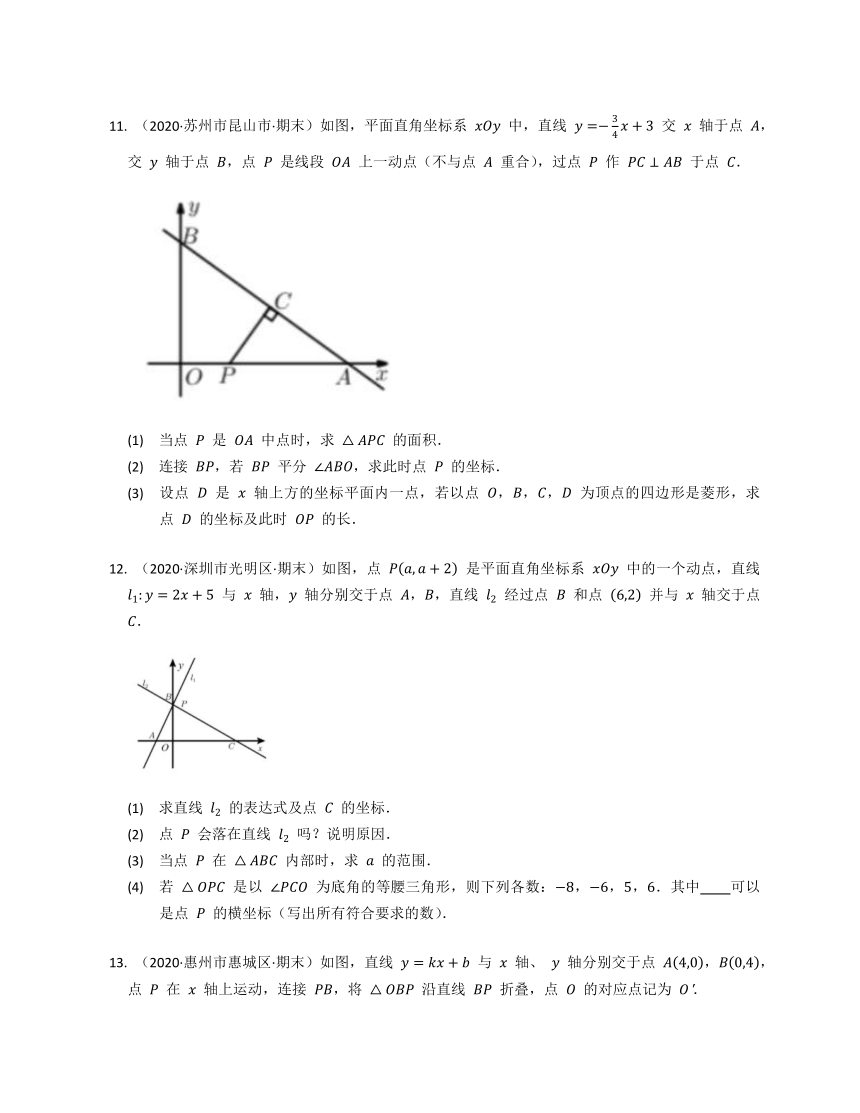
(2020·重庆渝中区·期末)如图,直线
与
轴、
轴分别相交于点
、点
.
(1)
求点
、点
的坐标.
(2)
将直线
向上平移
个单位得直线
,若
为直线
上一点,且
,求点
的坐标.
(2021·深圳市福田区·期末)如图,直线
交
轴和
轴于点
和点
,点
在
轴上,连接
,点
为直线
上一动点.
(1)
直线
的解析式为
.
(2)
若
,求点
的坐标.
(3)
当
时,求直线
的解析式及
的长.
(2019·福州市仓山区·期中)如图,直线
与
轴交于点
,与
轴交于点
、点
与点
关于
轴对称.
(1)
求直线
的函数表达式.
(2)
设点
是
轴上的一个动点,过点
作
轴的平行线,交直线
于点
,交直线
于点
,连接
.
①若
,求点
的坐标.
②若
的面积为
,请直接写出点
的坐标.
(2020·成都市青羊区·期末)如图
,在平面直角坐标系
中,已知直线
与直线
相交于点
,分别交坐标轴于点
,,,,点
是线段
延长线上的一个点,
的面积为
.
(1)
求直线
解析式和点
的坐标.
(2)
在()的条件下,平面直角坐标系内存在点
,使得以点
,,,
为顶点的四边形是平行四边形,请直接写出点
的坐标.
(3)
如图
,当点
为直线
上的一个动点时,将
绕点
逆时针旋转
得到
,连接
与
.点
随着点
的运动而运动,请求出点
运动所形成直线的解析式,以及
的最小值.
(2020·苏州市昆山市·期末)如图,平面直角坐标系
中,直线
交
轴于点
,交
轴于点
,点
是线段
上一动点(不与点
重合),过点
作
于点
.
(1)
当点
是
中点时,求
的面积.
(2)
连接
,若
平分
,求此时点
的坐标.
(3)
设点
是
轴上方的坐标平面内一点,若以点
,,,
为顶点的四边形是菱形,求点
的坐标及此时
的长.
(2020·深圳市光明区·期末)如图,点
是平面直角坐标系
中的一个动点,直线
与
轴,
轴分别交于点
,,直线
经过点
和点
并与
轴交于点
.
(1)
求直线
的表达式及点
的坐标.
(2)
点
会落在直线
吗?说明原因.
(3)
当点
在
内部时,求
的范围.
(4)
若
是以
为底角的等腰三角形,则下列各数:,,,.其中
可以是点
的横坐标(写出所有符合要求的数).
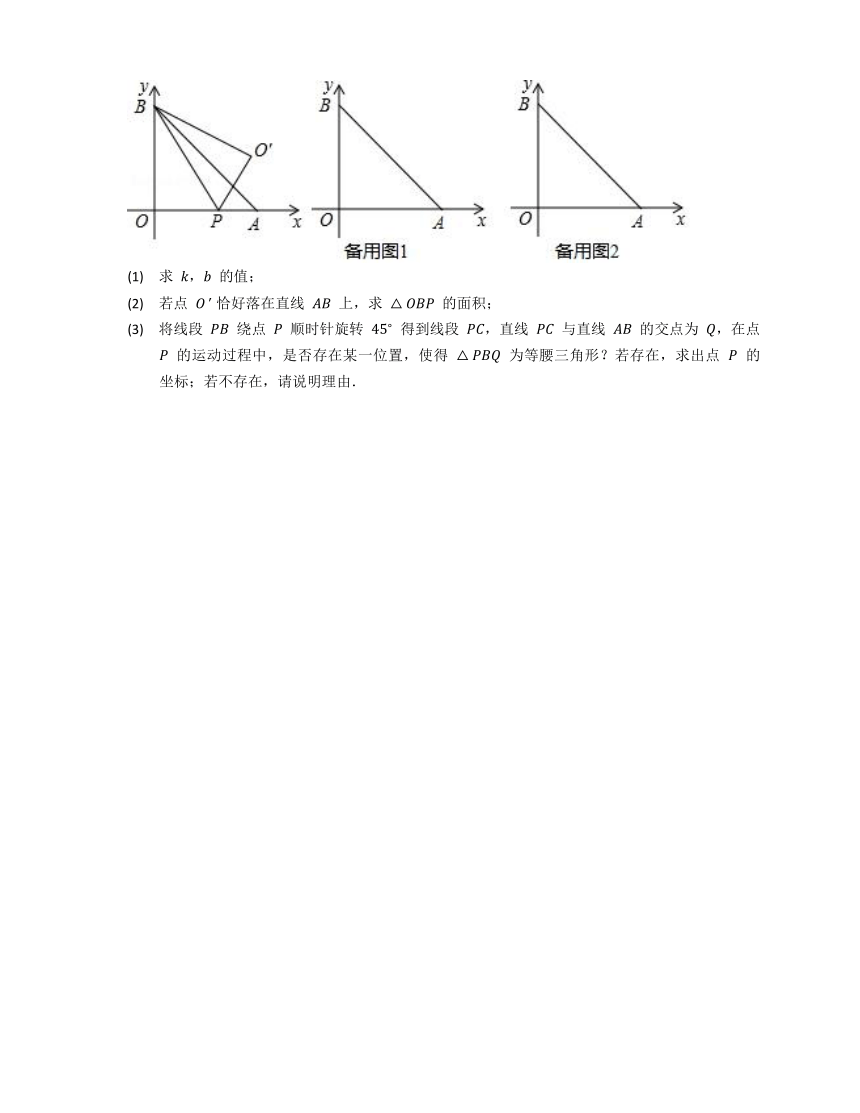
(2020·惠州市惠城区·期末)如图,直线
与
轴、
轴分别交于点
,,点
在
轴上运动,连接
,将
沿直线
折叠,点
的对应点记为
.
(1)
求
,
的值;
(2)
若点
恰好落在直线
上,求
的面积;
(3)
将线段
绕点
顺时针旋转
得到线段
,直线
与直线
的交点为
,在点
的运动过程中,是否存在某一位置,使得
为等腰三角形?若存在,求出点
的坐标;若不存在,请说明理由.
答案
一、选择题
1.
【答案】C
2.
【答案】B
3.
【答案】A
二、填空题
4.
【答案】
5.
【答案】
6.
【答案】
三、解答题
7.
【答案】
(1)
当
,则
,
解得
;
当
时,,
点
的坐标为
,点
的坐标为
.
(2)
将直线
向上平移
个单位得直线
,
设
的坐标为
,
,
,
,解得
或
,
点坐标为
或
.
8.
【答案】
(1)
(2)
点
,点
,点
,
,,
,
设点
,
当点
在线段
上时,
,
,
,
,
点
,
当点
在
的延长线上时,
,
,
,
,
点
.
综上所述:点
坐标为
或
.
(3)
如图,当点
在线段
上时,设
与
交于点
,
在
和
中,
,
,
点
坐标为
,
设直线
解析式
,
由题意可得
解得:
直线
解析式为
,
联立方程组得:
解得:
点
,
,
当点
在
延长线上时,设
与
轴交于
,
同理可求直线
解析式为
,
联立方程组
点
,
.
综上所述:
的解析式为:
或
;
的长为
或
.
9.
【答案】
(1)
对于
,令
,,
,
令
,
,
,
,
点
与点
关于
轴对称,
,
设直线
的解析式为
,
直线
的解析式为
.
(2)
①设点
,
,
,,
,,,
,
是直角三角形,
,
,
,
.
②
.
10.
【答案】
(1)
在
上,
,
,
也在直线
上,
,,
,,
令
,,
,,
令
,,
,
在
延长线上,设
,
,
.
(2)
.
(3)
过
作
轴,且使
,连接
交
于
点,
,,
,
,
,
,
又
,
,
,
,
,
,
,
运动所形成的直线是过
点且垂直于
的直线,
轴,,
,
,,
,
把
代入得
,,
,
过
作
于
点,
当
时,,
,
,
联立
解得
,
,
最小值为
.
11.
【答案】
(1)
直线
交
轴于点
,交
轴于点
,
时,,即
点坐标为
,
时,,即
点坐标为
,
,,
.
点
是
中点,
,
,
,
,
中,,
,
,
故
的面积为
.
(2)
设
点坐标为
,则
,
,,
,,,
,
则
,
,
,,
,
故点
的坐标为
.
(3)
设
点坐标为
,
如图所示,过点
作
轴于点
,
,
轴,
,,
,
,,
点坐标为
,
,,
,
,
.
,
,
,
当
时,即
.
为等腰三角形,将等腰
沿底边
翻折得到等腰
,
此时
,则以点
,,,
为顶点的四边形为菱形,
,
,
,(与
点重合,舍掉).
菱形
对角线
与
互相平分,由中点坐标公式得:
则
点坐标为
.
,
点坐标为
,
.
当
时,即
.
为等腰三角形,将等腰
沿
边翻折得到等腰
,
此时
,
则以顶点
,,,
为顶点的四边形
为菱形,
点
在线段
的垂直平分线上,
,
解得
,
,即
点坐标为
.
菱形
关于对角线
对称,
在
轴上,
点与
点关于
轴对称,
点坐标为
.
.
当
时,即
.
为等腰三角形,将等腰
沿
边翻折得到
为等腰三角形,此时
,
则以顶点
,,,
为顶点的四边形
为菱形,
,
,
又
则
.
又点
为
轴上方一点,
,即
,,
点坐标为
,
此时
点在
轴负半轴上,
.
综上所述,
点坐标为
,
或
点坐标为
,
或
点坐标为
,.
12.
【答案】
(1)
直线
与
,
轴分别交于
,
两点,
,,
设直线
解析式为
,
直线
经过点
和点
,
解得
直线
表达式为
,
直线
与
轴交于点
,
点坐标为
.
(2)
若
会落在直线
上,
则
满足
解析式,
,
解得:,
即
,
故
会落在直线
上.
(3)
若点
在
内部,
,且点
在直线
,
下方,
即
,
故当点
在
内部时,.
(4)
或
或
13.
【答案】
(1)
点
,
在直线
上,
解得:,.
(2)
存在两种情况:
①如图
,当
在
轴的正半轴上时,点
恰好落在直线
上,则
,
,
,
是等腰直角三角形,
,,
由折叠得:,,
(),
,
,
中,,
.
②如图
所示:当
在
轴的负半轴时,
由折叠得:,,
,
,
.
(3)
分
种情况:
①当
时,如图
,
与
重合,此时点
的坐标为
;
②当
时,如图
,
,
,
,
,
,
,
,
;
③当
时,如图
,此时
与
重合,
,
,
中,,
,
,
,
,
;
④当
时,如图
,此时
与
重合,则
与
关于
轴对称,
此时
;
综上,点
的坐标是
或
或
或
.
一、选择题
(2021·深圳市福田区·期末)如图,在平面直角坐标系中,已知一次函数
分别交
轴、
轴与点
,,若点
是坐标轴上的点,且
为等腰三角形,则满足条件的点
有
A.
个
B.
个
C.
个
D.
个
(2020·广东深圳市·模拟)如图,在平面直角坐标系中,直线
与
轴,
轴分别交于点
和点
,直线
与直线
在第一象限交于点
.若
,则
的值为
A.
B.
C.
D.
(2020·专项)一次函数
满足
,且
随
的增大而减小,则此函数的图象不经过
A.第一象限
B.第二象限
C.第三象限
D.第四象限
二、填空题
(2021·上海闵行区·单元测试)当
时,一次函数的图象
不经过原点.
(2021·山东·同步练习)如图,有一条折线
,它是由过
,,
的折线依次平移
,,,
个单位得到的,直线
与此折线恰有
(,且
为整数)个交点,则
的值为
.
(2021·深圳市福田区·期末)如图,直线
交
轴于点
,交
轴于点
,点
和点
关于
轴对称,连接
,点
是
外一点,,点
是
上一点,点
是
上一点,且
,连接
,.若
,则
的值为
.
三、解答题
(2020·重庆渝中区·期末)如图,直线
与
轴、
轴分别相交于点
、点
.
(1)
求点
、点
的坐标.
(2)
将直线
向上平移
个单位得直线
,若
为直线
上一点,且
,求点
的坐标.
(2021·深圳市福田区·期末)如图,直线
交
轴和
轴于点
和点
,点
在
轴上,连接
,点
为直线
上一动点.
(1)
直线
的解析式为
.
(2)
若
,求点
的坐标.
(3)
当
时,求直线
的解析式及
的长.
(2019·福州市仓山区·期中)如图,直线
与
轴交于点
,与
轴交于点
、点
与点
关于
轴对称.
(1)
求直线
的函数表达式.
(2)
设点
是
轴上的一个动点,过点
作
轴的平行线,交直线
于点
,交直线
于点
,连接
.
①若
,求点
的坐标.
②若
的面积为
,请直接写出点
的坐标.
(2020·成都市青羊区·期末)如图
,在平面直角坐标系
中,已知直线
与直线
相交于点
,分别交坐标轴于点
,,,,点
是线段
延长线上的一个点,
的面积为
.
(1)
求直线
解析式和点
的坐标.
(2)
在()的条件下,平面直角坐标系内存在点
,使得以点
,,,
为顶点的四边形是平行四边形,请直接写出点
的坐标.
(3)
如图
,当点
为直线
上的一个动点时,将
绕点
逆时针旋转
得到
,连接
与
.点
随着点
的运动而运动,请求出点
运动所形成直线的解析式,以及
的最小值.
(2020·苏州市昆山市·期末)如图,平面直角坐标系
中,直线
交
轴于点
,交
轴于点
,点
是线段
上一动点(不与点
重合),过点
作
于点
.
(1)
当点
是
中点时,求
的面积.
(2)
连接
,若
平分
,求此时点
的坐标.
(3)
设点
是
轴上方的坐标平面内一点,若以点
,,,
为顶点的四边形是菱形,求点
的坐标及此时
的长.
(2020·深圳市光明区·期末)如图,点
是平面直角坐标系
中的一个动点,直线
与
轴,
轴分别交于点
,,直线
经过点
和点
并与
轴交于点
.
(1)
求直线
的表达式及点
的坐标.
(2)
点
会落在直线
吗?说明原因.
(3)
当点
在
内部时,求
的范围.
(4)
若
是以
为底角的等腰三角形,则下列各数:,,,.其中
可以是点
的横坐标(写出所有符合要求的数).
(2020·惠州市惠城区·期末)如图,直线
与
轴、
轴分别交于点
,,点
在
轴上运动,连接
,将
沿直线
折叠,点
的对应点记为
.
(1)
求
,
的值;
(2)
若点
恰好落在直线
上,求
的面积;
(3)
将线段
绕点
顺时针旋转
得到线段
,直线
与直线
的交点为
,在点
的运动过程中,是否存在某一位置,使得
为等腰三角形?若存在,求出点
的坐标;若不存在,请说明理由.
答案
一、选择题
1.
【答案】C
2.
【答案】B
3.
【答案】A
二、填空题
4.
【答案】
5.
【答案】
6.
【答案】
三、解答题
7.
【答案】
(1)
当
,则
,
解得
;
当
时,,
点
的坐标为
,点
的坐标为
.
(2)
将直线
向上平移
个单位得直线
,
设
的坐标为
,
,
,
,解得
或
,
点坐标为
或
.
8.
【答案】
(1)
(2)
点
,点
,点
,
,,
,
设点
,
当点
在线段
上时,
,
,
,
,
点
,
当点
在
的延长线上时,
,
,
,
,
点
.
综上所述:点
坐标为
或
.
(3)
如图,当点
在线段
上时,设
与
交于点
,
在
和
中,
,
,
点
坐标为
,
设直线
解析式
,
由题意可得
解得:
直线
解析式为
,
联立方程组得:
解得:
点
,
,
当点
在
延长线上时,设
与
轴交于
,
同理可求直线
解析式为
,
联立方程组
点
,
.
综上所述:
的解析式为:
或
;
的长为
或
.
9.
【答案】
(1)
对于
,令
,,
,
令
,
,
,
,
点
与点
关于
轴对称,
,
设直线
的解析式为
,
直线
的解析式为
.
(2)
①设点
,
,
,,
,,,
,
是直角三角形,
,
,
,
.
②
.
10.
【答案】
(1)
在
上,
,
,
也在直线
上,
,,
,,
令
,,
,,
令
,,
,
在
延长线上,设
,
,
.
(2)
.
(3)
过
作
轴,且使
,连接
交
于
点,
,,
,
,
,
,
又
,
,
,
,
,
,
,
运动所形成的直线是过
点且垂直于
的直线,
轴,,
,
,,
,
把
代入得
,,
,
过
作
于
点,
当
时,,
,
,
联立
解得
,
,
最小值为
.
11.
【答案】
(1)
直线
交
轴于点
,交
轴于点
,
时,,即
点坐标为
,
时,,即
点坐标为
,
,,
.
点
是
中点,
,
,
,
,
中,,
,
,
故
的面积为
.
(2)
设
点坐标为
,则
,
,,
,,,
,
则
,
,
,,
,
故点
的坐标为
.
(3)
设
点坐标为
,
如图所示,过点
作
轴于点
,
,
轴,
,,
,
,,
点坐标为
,
,,
,
,
.
,
,
,
当
时,即
.
为等腰三角形,将等腰
沿底边
翻折得到等腰
,
此时
,则以点
,,,
为顶点的四边形为菱形,
,
,
,(与
点重合,舍掉).
菱形
对角线
与
互相平分,由中点坐标公式得:
则
点坐标为
.
,
点坐标为
,
.
当
时,即
.
为等腰三角形,将等腰
沿
边翻折得到等腰
,
此时
,
则以顶点
,,,
为顶点的四边形
为菱形,
点
在线段
的垂直平分线上,
,
解得
,
,即
点坐标为
.
菱形
关于对角线
对称,
在
轴上,
点与
点关于
轴对称,
点坐标为
.
.
当
时,即
.
为等腰三角形,将等腰
沿
边翻折得到
为等腰三角形,此时
,
则以顶点
,,,
为顶点的四边形
为菱形,
,
,
又
则
.
又点
为
轴上方一点,
,即
,,
点坐标为
,
此时
点在
轴负半轴上,
.
综上所述,
点坐标为
,
或
点坐标为
,
或
点坐标为
,.
12.
【答案】
(1)
直线
与
,
轴分别交于
,
两点,
,,
设直线
解析式为
,
直线
经过点
和点
,
解得
直线
表达式为
,
直线
与
轴交于点
,
点坐标为
.
(2)
若
会落在直线
上,
则
满足
解析式,
,
解得:,
即
,
故
会落在直线
上.
(3)
若点
在
内部,
,且点
在直线
,
下方,
即
,
故当点
在
内部时,.
(4)
或
或
13.
【答案】
(1)
点
,
在直线
上,
解得:,.
(2)
存在两种情况:
①如图
,当
在
轴的正半轴上时,点
恰好落在直线
上,则
,
,
,
是等腰直角三角形,
,,
由折叠得:,,
(),
,
,
中,,
.
②如图
所示:当
在
轴的负半轴时,
由折叠得:,,
,
,
.
(3)
分
种情况:
①当
时,如图
,
与
重合,此时点
的坐标为
;
②当
时,如图
,
,
,
,
,
,
,
,
;
③当
时,如图
,此时
与
重合,
,
,
中,,
,
,
,
,
;
④当
时,如图
,此时
与
重合,则
与
关于
轴对称,
此时
;
综上,点
的坐标是
或
或
或
.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
