2020-2021学年八年级数学青岛版下册《6.3特殊平行四边形—矩形》同步提升训练(word版、含解析)
文档属性
| 名称 | 2020-2021学年八年级数学青岛版下册《6.3特殊平行四边形—矩形》同步提升训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 309.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 18:00:50 | ||
图片预览




文档简介
青岛版2021年度八年级数学下册《6.3特殊平行四边形—矩形》同步提升训练(附答案)
一、选择题
1.如图,点P是Rt△ABC中斜边AC(不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( )
A.1.5
B.2
C.4.8
D.2.4
2.下列说法正确的是( )
A.矩形的对角线互相垂直且平分
B.矩形的邻边一定相等
C.对角线相等的四边形是矩形
D.有三个角为直角的四边形为矩形
3.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OCD的度数为( )
A.35°
B.40°
C.45°
D.50°
4.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
A.3
B.
C.
D.4
5.如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
A.2
B.2
C.3
D.3
6.如图,已知在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O,若AO=BO,AD=3,AB=2,则四边形ABCD的面积为( )
A.4
B.5
C.6
D.7
二、填空题
7.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为
.
8.如图,在Rt△ABC中,∠BAC=90°,BA=5,AC=8,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN长的最小值为
.
9.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止(同时点Q也停止),这段时间内,当运动时间为
时,P、Q、C、D四点组成矩形.
10.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和1cm/s,则最快
s后,四边ABPQ成为矩形.
11.下列命题:
①矩形的对角线互相平分且相等;②对角线相等的四边形是矩形;
③菱形的每一条对角线平分一组对角;④一条对角线平分一组对角的平行四边形是菱形.
其中正确的命题为
(注:把你认为正确的命题序号都填上)
12.如图,若将四根木条钉成的矩形木框变成?ABCD的形状,并使其面积变为矩形面积的一半,则?ABCD的最小内角的度数为
.
13.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是
.
14.在平行四边形ABCD中,AB=5,BC=6,若AC=BD,则平行四边形ABCD的面积为
.
15.如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是
.
16.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足
(关系)时,四边形EFGH为矩形.
三、解答题
17.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
18.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
19.已知菱形ABCD中,延长DC至点E,使CE=CD,延长BC至点F,使CF=CB,分别连接DB、BE、EF、FD.
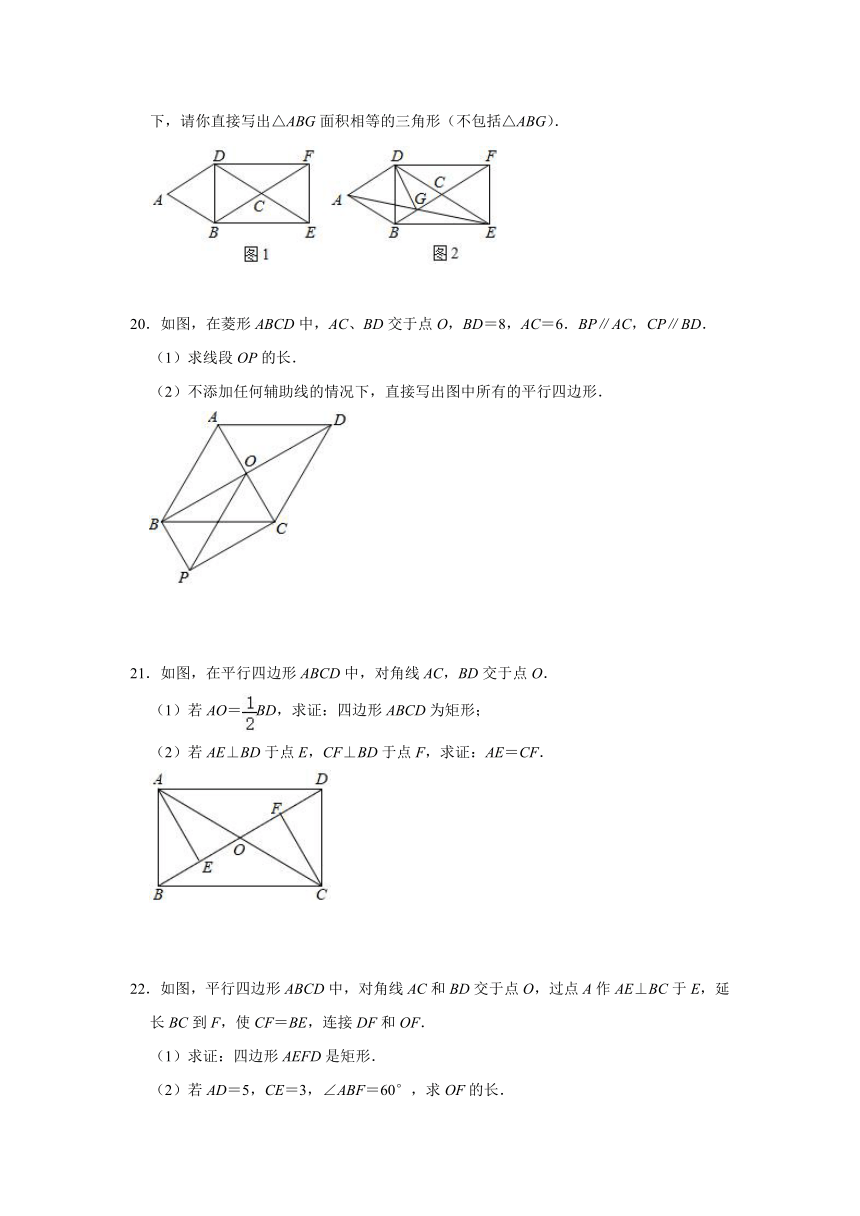
(1)如图1,求证:四边形DBEF是矩形;
(2)如图2,∠DFB=30°,连接AE交BF于点G,连接DG,在不添加辅助线的情况下,请你直接写出△ABG面积相等的三角形(不包括△ABG).
20.如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=6.BP∥AC,CP∥BD.
(1)求线段OP的长.
(2)不添加任何辅助线的情况下,直接写出图中所有的平行四边形.
21.如图,在平行四边形ABCD中,对角线AC,BD交于点O.
(1)若AO=BD,求证:四边形ABCD为矩形;
(2)若AE⊥BD于点E,CF⊥BD于点F,求证:AE=CF.
22.如图,平行四边形ABCD中,对角线AC和BD交于点O,过点A作AE⊥BC于E,延长BC到F,使CF=BE,连接DF和OF.
(1)求证:四边形AEFD是矩形.
(2)若AD=5,CE=3,∠ABF=60°,求OF的长.
23.如图所示,已知AB∥CD,AB=CD,∠A=∠D.
(1)求证:四边形ABCD为矩形;
(2)若点E是AB边上的中点,点F为AD边上一点,∠1=2∠2,CF=5,求AF+BC的值.
24.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
参考答案
1.解:∵∠ABC=90°,AB=6,BC=8,
∴AC===10,
∵PM⊥AB,PN⊥BC,∠C=90°,
∴四边形BNPM是矩形,
∴MN=BP,
由垂线段最短可得BP⊥AC时,线段MN的值最小,
此时,S△ABC=BC?AB=AC?BP,
即×8×6=×10?BP,
解得:BP=4.8,
即MN的最小值是4.8,
故选:C.
2.解:A、∵矩形的对角线互相平分且相等,
∴选项A不符合题意;
B、∵矩形的邻边一定垂直,不一定相等,
∴选项B不符合题意;
C、∵对角线相等的平行四边形是矩形,
∴选项C不符合题意;
D、∵有三个角为直角的四边形为矩形,
∴选项D符合题意;
故选:D.
3.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,AB∥CD,
∴∠OAB=∠DAB﹣∠OAD=90°﹣55°=35°,∠OCD=∠OAB=35°,
故选:A.
4.解:∵四边形COED是矩形,
∴CE=OD,
∵点D的坐标是(1,3),
∴OD==,
∴CE=,
故选:C.
5.解:连接CF,如图所示:
∵DE是AC的中垂线,
∴AF=CF,∠CDE=90°,
∴∠ACF=∠A=30°,
∴∠CFB=∠A+∠ACF=60°,
∵AF=BF,
∴CF=BF,
∴△BCF是等边三角形,
∴CF=BC=2,∠BCF=60°,
∴CD=CF?cos30°=,∠BCD=60°+30°=90°,
∵BE⊥DF,
∴∠E=90°,
∴四边形BCDE是矩形,
∴四边形BCDE的面积=BC?CD=2×=2;
故选:A.
6.解:∵AB=DC,AD=BC,
∴四边形ABCD为平行四边形,
∴AO=OC,BO=DO,
∵AO=BO,
∴AC=BD,
∴四边形ABCD为矩形,
∵AD=3,AB=2,
∴四边形ABCD的面积为:AD?AB=2×3=6,
故选:C.
7.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
8.解:∵∠BAC=90°,且BA=5,AC=8,
∴BC===,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD===,
∴MN的最小值为,
故答案为:.
9.解:根据已知可知:当点P到达点D时,点Q将由C﹣B﹣C﹣B﹣C运动,
∵四边形ABCD是矩形,
∴AD∥BC,∠D=90°,
∴PD∥CQ,
若PD=CQ,则四边形APQB是矩形,
由题意得DP=12﹣t,
当0≤t≤3时,CQ=4t,12﹣t=4t,
∴t=2.4(s),
当3<t≤6时,CQ=24﹣4t,12﹣t=24﹣4t,
∴t=4(s),
当6<t≤9时,CQ=4t﹣24,12﹣t=4t﹣24,
∴t=7.3(s);
当9<t≤12时,CQ=48﹣4t,12﹣t=48﹣4t,
∴t=12(s),此时PQ与DC重合,无法构成矩形,故舍去,
故答案为:2.4s或4s或7.2s.
10.解:∵四边形ABCD是矩形
∴∠A=∠B=90°,AD=BC=20cm,
设最快x秒,四边形ABPQ成为矩形,
∵四边形ABPQ是矩形
∴AQ=BP
∴3x=20﹣x
∴x=5
故答案为:5
11.解:①矩形的对角线互相平分且相等;故正确;
②对角线相等的四边形是矩形,不能正确判定,故错误;
③菱形的每一条对角线平分一组对角,这是菱形的一条重要性质,故正确;
④一条对角线平分一组对角的平行四边形是菱形,故正确.
故答案为:①③④.
12.解:如图,过点A作AE⊥BC于点E,
∵平行四边形的面积为矩形的一半且同底BC,
∴平行四边形ABCD的高AE是矩形宽AB的一半.
在直角三角形ABE中,AE=AB,
∴∠ADC=30°.
故答案为:30°.
13.解:连接AP,
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∵∠BAC=90°,M为EF中点,
∴AM=EF=AP,
∵在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
∴BC==5,
当AP⊥BC时,AP值最小,
此时S△BAC=×3×4=×5×AP,
∴AP=,即AP的范围是AP≥,
∴2AM≥,
∴AM的范围是AM≥,
∵AP<AC,
∴AP<4,
∴AM<2,
∴≤AM<2.
故答案为:≤AM<2.
14.解:∵平行四边形ABCD中,AC=BD
∴四边形ABCD是矩形.
∴矩形ABCD的面积是:5×6=30.
故答案为:30.
15.解:∵AE∥BD,
∴∠CDB=∠DAE,
∵∠ACB=90°,DE⊥AC,
∴∠C=∠ADE=90°,
∴DE∥BC,
∵D为AC中点,
∴AD=CD,
在△ADE和△DCB中
∵,
∴△ADE≌△DCB(ASA),
∴DE=BC=4,
在Rt△DCB中,BC=4,BD=5,由勾股定理得:DC=3,
∴AD=DC=3,
∵ED=BC,DE∥BC,
∴四边形DEBC是平行四边形,
∴CD=BE=3,
∴四边形ACBE的周长是AC+BC+BE+AE=3+3+4+3+5=18,
故答案为:18.
16.解:∵四边形ABCD是矩形,
∴∠A=90°.
∵AE=AF,
∴∠AFE=∠AEF=45°.
又∵EH⊥EF,FG⊥EF
∴∠GFB=∠HED=45°,
∴△DHE和△BGF都是等腰直角三角形.
如果四边形EFGH是矩形,则EH=FG,
∴ED=FB
又∵AE=AF,
∴AD=AB.
故答案是:AD=AB.
17.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=12﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,
∴AD===6,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,
,
∴Rt△ADE≌Rt△GDE(HL),
∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,
即(8﹣AE)2=AE2+42,
解得:AE=3.
19.(1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形,
∵四边形ABCD是菱形,
∴CD=CB,
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形;
(2)解:∵四边形DBEF是矩形,
∴∠BDF=90°,CD=CE,
∵∠DFB=30°,
∴∠DBF=60°,
∵四边形ABCD是菱形,
∴AB=CD=CE,AD∥BG,AB∥CE,
∴∠ABG=∠ECG,∠BAG=∠CEG,
在△ABG和△ECG中,
,
∴△ABG≌△ECG(ASA),
∴S△ABG=S△ECG,BG=CG,AG=EG,
∴S△BDG=S△CDG,S△ABG=S△BEG,
∵AD∥BG,
∴S△ABG=S△BDG,
∴S△ABG=S△BDG=S△ECG=S△CDG=S△BEG,
∴△ABG面积相等的三角形是△BDG、△ECG、△CDG、△BEG.
20.解:(1)∵DP∥AC,CP∥BD,
∴四边形OCPD是平行时四边形,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=OC=3,OB=OD=4,
∴∠COD=90°,
∴四边形OCPD是矩形,
∴CD=OP.
在Rt△COD中,CD=,
∴OP=CD=5.
(2)四边形ABCD、四边形BOPC、四边形OCPD、四边形AOPD都是平行四边形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=BD,
∴OA=OC=OB=OD,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEB=∠CFD=90°,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF.
22.(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形AEFD是矩形;
(2)解:由(1)知:四边形AEFD是矩形,
∴EF=AD=5,
∵四边形ABCD是平行四边形,
∴BC=AD=5,OB=OD,
∵EC=3,
∴BE=CF=2,
∴BF=BC+CF=7,
Rt△ABE中,∠ABE=60°,
∴∠BAE=30°,
∴AB=2BE=4,
∴DF=AE===2,
∴BD===,
∵OB=OD,∠DFC=90°,
∴OF=BD=.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A+∠D=180°,
又∠A=∠D,
∴∠A=∠D=90°,
∴平行四边形ABCD为矩形;
(2)解:延长DA,CE交于点G,
∵四边形ABCD是矩形,
∴∠DAB=∠B=90°,AD∥BC,
∴∠GAE=90°,∠G=∠ECB,
∵E是AB边的中点,
∴AE=BE,
在△AGE和△BCE中,,
∴△AGE≌△BCE(AAS),
∴AG=BC,∠G=∠2,
∴AF+BC=AF+AG=FG,
∵∠1=∠2+∠G=2∠2,
∴∠2=∠G,
∴FG=CF=5,
∴AF+BC=5.
24.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AD=10,
∴AD=AB=BC=10,
∵EC=4,
∴BE=10﹣4=6,
在Rt△ABE中,AE=,
在Rt△AEC中,AC=,
∵四边形ABCD是菱形,
∴OA=OC,
∴OE=AC=
一、选择题
1.如图,点P是Rt△ABC中斜边AC(不与A,C重合)上一动点,分别作PM⊥AB于点M,作PN⊥BC于点N,连接BP、MN,若AB=6,BC=8,当点P在斜边AC上运动时,则MN的最小值是( )
A.1.5
B.2
C.4.8
D.2.4
2.下列说法正确的是( )
A.矩形的对角线互相垂直且平分
B.矩形的邻边一定相等
C.对角线相等的四边形是矩形
D.有三个角为直角的四边形为矩形
3.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OCD的度数为( )
A.35°
B.40°
C.45°
D.50°
4.如图,在矩形COED中,点D的坐标是(1,3),则CE的长是( )
A.3
B.
C.
D.4
5.如图,△ABC中,AC的中垂线交AC、AB于点D、F,BE⊥DF交DF延长线于点E,若∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
A.2
B.2
C.3
D.3
6.如图,已知在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O,若AO=BO,AD=3,AB=2,则四边形ABCD的面积为( )
A.4
B.5
C.6
D.7
二、填空题
7.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE,设AC=12,BD=16,则OE的长为
.
8.如图,在Rt△ABC中,∠BAC=90°,BA=5,AC=8,D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN长的最小值为
.
9.如图,在矩形ABCD中,AB=4cm,AD=12cm,点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止(同时点Q也停止),这段时间内,当运动时间为
时,P、Q、C、D四点组成矩形.
10.如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和1cm/s,则最快
s后,四边ABPQ成为矩形.
11.下列命题:
①矩形的对角线互相平分且相等;②对角线相等的四边形是矩形;
③菱形的每一条对角线平分一组对角;④一条对角线平分一组对角的平行四边形是菱形.
其中正确的命题为
(注:把你认为正确的命题序号都填上)
12.如图,若将四根木条钉成的矩形木框变成?ABCD的形状,并使其面积变为矩形面积的一半,则?ABCD的最小内角的度数为
.
13.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点(P不与B、C重合),PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的取值范围是
.
14.在平行四边形ABCD中,AB=5,BC=6,若AC=BD,则平行四边形ABCD的面积为
.
15.如图,在△ABC中,∠ACB=90°.D是AC的中点,DE⊥AC,AE∥BD,若BC=4,AE=5,则四边形ACBE的周长是
.
16.如图,在矩形ABCD中,AE=AF,过点E作EH⊥EF交DC于点H,过F作FG⊥EF交BC于G,当AD、AB满足
(关系)时,四边形EFGH为矩形.
三、解答题
17.如图,在平行四边形ABCD中,P是AB上一点(不与点A,B重合),CP=CD,过点P作PQ⊥CP,交AD于点Q,连接CQ,∠BPC=∠AQP.
(1)求证:四边形ABCD是矩形;
(2)当AP=3,AD=9时,求AQ和CQ的长.
18.如图,在平行四边形ABCD中,AC,BD交于点O,且AO=BO,∠ADB的平分线DE交AB于点E.
(1)求证:四边形ABCD是矩形.
(2)若AB=8,OC=5,求AE的长.
19.已知菱形ABCD中,延长DC至点E,使CE=CD,延长BC至点F,使CF=CB,分别连接DB、BE、EF、FD.
(1)如图1,求证:四边形DBEF是矩形;
(2)如图2,∠DFB=30°,连接AE交BF于点G,连接DG,在不添加辅助线的情况下,请你直接写出△ABG面积相等的三角形(不包括△ABG).
20.如图,在菱形ABCD中,AC、BD交于点O,BD=8,AC=6.BP∥AC,CP∥BD.
(1)求线段OP的长.
(2)不添加任何辅助线的情况下,直接写出图中所有的平行四边形.
21.如图,在平行四边形ABCD中,对角线AC,BD交于点O.
(1)若AO=BD,求证:四边形ABCD为矩形;
(2)若AE⊥BD于点E,CF⊥BD于点F,求证:AE=CF.
22.如图,平行四边形ABCD中,对角线AC和BD交于点O,过点A作AE⊥BC于E,延长BC到F,使CF=BE,连接DF和OF.
(1)求证:四边形AEFD是矩形.
(2)若AD=5,CE=3,∠ABF=60°,求OF的长.
23.如图所示,已知AB∥CD,AB=CD,∠A=∠D.
(1)求证:四边形ABCD为矩形;
(2)若点E是AB边上的中点,点F为AD边上一点,∠1=2∠2,CF=5,求AF+BC的值.
24.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)连接OE,若AD=10,EC=4,求OE的长度.
参考答案
1.解:∵∠ABC=90°,AB=6,BC=8,
∴AC===10,
∵PM⊥AB,PN⊥BC,∠C=90°,
∴四边形BNPM是矩形,
∴MN=BP,
由垂线段最短可得BP⊥AC时,线段MN的值最小,
此时,S△ABC=BC?AB=AC?BP,
即×8×6=×10?BP,
解得:BP=4.8,
即MN的最小值是4.8,
故选:C.
2.解:A、∵矩形的对角线互相平分且相等,
∴选项A不符合题意;
B、∵矩形的邻边一定垂直,不一定相等,
∴选项B不符合题意;
C、∵对角线相等的平行四边形是矩形,
∴选项C不符合题意;
D、∵有三个角为直角的四边形为矩形,
∴选项D符合题意;
故选:D.
3.解:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OD,
∴AC=BD,
∴四边形ABCD是矩形,
∴∠DAB=90°,AB∥CD,
∴∠OAB=∠DAB﹣∠OAD=90°﹣55°=35°,∠OCD=∠OAB=35°,
故选:A.
4.解:∵四边形COED是矩形,
∴CE=OD,
∵点D的坐标是(1,3),
∴OD==,
∴CE=,
故选:C.
5.解:连接CF,如图所示:
∵DE是AC的中垂线,
∴AF=CF,∠CDE=90°,
∴∠ACF=∠A=30°,
∴∠CFB=∠A+∠ACF=60°,
∵AF=BF,
∴CF=BF,
∴△BCF是等边三角形,
∴CF=BC=2,∠BCF=60°,
∴CD=CF?cos30°=,∠BCD=60°+30°=90°,
∵BE⊥DF,
∴∠E=90°,
∴四边形BCDE是矩形,
∴四边形BCDE的面积=BC?CD=2×=2;
故选:A.
6.解:∵AB=DC,AD=BC,
∴四边形ABCD为平行四边形,
∴AO=OC,BO=DO,
∵AO=BO,
∴AC=BD,
∴四边形ABCD为矩形,
∵AD=3,AB=2,
∴四边形ABCD的面积为:AD?AB=2×3=6,
故选:C.
7.解:∵DE∥AC,CE∥BD,
∴四边形OCED为平行四边形,
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=AC=6,OB=OD=BD=8,
∴∠DOC=90°,CD===10,
∴平行四边形OCED为矩形,
∴OE=CD=10,
故答案为:10.
8.解:∵∠BAC=90°,且BA=5,AC=8,
∴BC===,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD===,
∴MN的最小值为,
故答案为:.
9.解:根据已知可知:当点P到达点D时,点Q将由C﹣B﹣C﹣B﹣C运动,
∵四边形ABCD是矩形,
∴AD∥BC,∠D=90°,
∴PD∥CQ,
若PD=CQ,则四边形APQB是矩形,
由题意得DP=12﹣t,
当0≤t≤3时,CQ=4t,12﹣t=4t,
∴t=2.4(s),
当3<t≤6时,CQ=24﹣4t,12﹣t=24﹣4t,
∴t=4(s),
当6<t≤9时,CQ=4t﹣24,12﹣t=4t﹣24,
∴t=7.3(s);
当9<t≤12时,CQ=48﹣4t,12﹣t=48﹣4t,
∴t=12(s),此时PQ与DC重合,无法构成矩形,故舍去,
故答案为:2.4s或4s或7.2s.
10.解:∵四边形ABCD是矩形
∴∠A=∠B=90°,AD=BC=20cm,
设最快x秒,四边形ABPQ成为矩形,
∵四边形ABPQ是矩形
∴AQ=BP
∴3x=20﹣x
∴x=5
故答案为:5
11.解:①矩形的对角线互相平分且相等;故正确;
②对角线相等的四边形是矩形,不能正确判定,故错误;
③菱形的每一条对角线平分一组对角,这是菱形的一条重要性质,故正确;
④一条对角线平分一组对角的平行四边形是菱形,故正确.
故答案为:①③④.
12.解:如图,过点A作AE⊥BC于点E,
∵平行四边形的面积为矩形的一半且同底BC,
∴平行四边形ABCD的高AE是矩形宽AB的一半.
在直角三角形ABE中,AE=AB,
∴∠ADC=30°.
故答案为:30°.
13.解:连接AP,
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∵∠BAC=90°,
∴四边形AEPF是矩形,
∴AP=EF,
∵∠BAC=90°,M为EF中点,
∴AM=EF=AP,
∵在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
∴BC==5,
当AP⊥BC时,AP值最小,
此时S△BAC=×3×4=×5×AP,
∴AP=,即AP的范围是AP≥,
∴2AM≥,
∴AM的范围是AM≥,
∵AP<AC,
∴AP<4,
∴AM<2,
∴≤AM<2.
故答案为:≤AM<2.
14.解:∵平行四边形ABCD中,AC=BD
∴四边形ABCD是矩形.
∴矩形ABCD的面积是:5×6=30.
故答案为:30.
15.解:∵AE∥BD,
∴∠CDB=∠DAE,
∵∠ACB=90°,DE⊥AC,
∴∠C=∠ADE=90°,
∴DE∥BC,
∵D为AC中点,
∴AD=CD,
在△ADE和△DCB中
∵,
∴△ADE≌△DCB(ASA),
∴DE=BC=4,
在Rt△DCB中,BC=4,BD=5,由勾股定理得:DC=3,
∴AD=DC=3,
∵ED=BC,DE∥BC,
∴四边形DEBC是平行四边形,
∴CD=BE=3,
∴四边形ACBE的周长是AC+BC+BE+AE=3+3+4+3+5=18,
故答案为:18.
16.解:∵四边形ABCD是矩形,
∴∠A=90°.
∵AE=AF,
∴∠AFE=∠AEF=45°.
又∵EH⊥EF,FG⊥EF
∴∠GFB=∠HED=45°,
∴△DHE和△BGF都是等腰直角三角形.
如果四边形EFGH是矩形,则EH=FG,
∴ED=FB
又∵AE=AF,
∴AD=AB.
故答案是:AD=AB.
17.(1)证明:∵∠BPQ=∠BPC+∠CPQ=∠A+∠AQP,∠BPC=∠AQP,
∴∠CPQ=∠A,
∵PQ⊥CP,
∴∠A=∠CPQ=90°,
∴平行四边形ABCD是矩形;
(2)解:∵四边形ABCD是矩形,
∴∠D=∠CPQ=90°,
在Rt△CDQ和Rt△CPQ中,
,
∴Rt△CDQ≌Rt△CPQ(HL),
∴DQ=PQ,
设AQ=x,则DQ=PQ=12﹣x,
在Rt△APQ中,AQ2+AP2=PQ2,
∴x2+32=(9﹣x)2,
解得:x=4,
∴AQ的长是4.
设CD=AB=CP=y,则PB=y﹣3,在Rt△PCB中,根据勾股定理列方程,求出y=15.
在Rt△CDQ中,CQ==5.
18.(1)证明:∵四边形ABCD是平行四边形,
∴AC=2AO,BD=2BO,
∵AO=BO,
∴AC=BD,
∴平行四边形ABCD为矩形;
(2)解:过点E作EG⊥BD于点G,如图所示:
∵四边形ABCD是矩形,OC=5,
∴∠BAD=90°,BD=AC=2OC=10.
在Rt△ABD中,AB=8,BD=10,
∴AD===6,
∵∠DAB=90°,
∴EA⊥AD,
∵DE为∠ADB的平分线,EG⊥BD,
∴EG=EA,∠EGB=90°.
在Rt△ADE和Rt△GDE中,
,
∴Rt△ADE≌Rt△GDE(HL),
∴AD=GD=6,
∴BG=BD﹣GD=10﹣6=4,
在Rt△BEG中,由勾股定理得:BE2=EG2+BG2,
即(8﹣AE)2=AE2+42,
解得:AE=3.
19.(1)证明:∵CE=CD,CF=CB,
∴四边形DBEF是平行四边形,
∵四边形ABCD是菱形,
∴CD=CB,
∴CE=CF,
∴BF=DE,
∴四边形DBEF是矩形;
(2)解:∵四边形DBEF是矩形,
∴∠BDF=90°,CD=CE,
∵∠DFB=30°,
∴∠DBF=60°,
∵四边形ABCD是菱形,
∴AB=CD=CE,AD∥BG,AB∥CE,
∴∠ABG=∠ECG,∠BAG=∠CEG,
在△ABG和△ECG中,
,
∴△ABG≌△ECG(ASA),
∴S△ABG=S△ECG,BG=CG,AG=EG,
∴S△BDG=S△CDG,S△ABG=S△BEG,
∵AD∥BG,
∴S△ABG=S△BDG,
∴S△ABG=S△BDG=S△ECG=S△CDG=S△BEG,
∴△ABG面积相等的三角形是△BDG、△ECG、△CDG、△BEG.
20.解:(1)∵DP∥AC,CP∥BD,
∴四边形OCPD是平行时四边形,
∵四边形ABCD是菱形,
∴BD⊥AC,AO=OC=3,OB=OD=4,
∴∠COD=90°,
∴四边形OCPD是矩形,
∴CD=OP.
在Rt△COD中,CD=,
∴OP=CD=5.
(2)四边形ABCD、四边形BOPC、四边形OCPD、四边形AOPD都是平行四边形.
21.证明:(1)∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=BD,
∴OA=OC=OB=OD,
∴AC=BD,
∴平行四边形ABCD是矩形;
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵AE⊥BD于点E,CF⊥BD于点F,
∴∠AEB=∠CFD=90°,
在△ABE与△CDF中,
,
∴△ABE≌△CDF(AAS),
∴AE=CF.
22.(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形AEFD是矩形;
(2)解:由(1)知:四边形AEFD是矩形,
∴EF=AD=5,
∵四边形ABCD是平行四边形,
∴BC=AD=5,OB=OD,
∵EC=3,
∴BE=CF=2,
∴BF=BC+CF=7,
Rt△ABE中,∠ABE=60°,
∴∠BAE=30°,
∴AB=2BE=4,
∴DF=AE===2,
∴BD===,
∵OB=OD,∠DFC=90°,
∴OF=BD=.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A+∠D=180°,
又∠A=∠D,
∴∠A=∠D=90°,
∴平行四边形ABCD为矩形;
(2)解:延长DA,CE交于点G,
∵四边形ABCD是矩形,
∴∠DAB=∠B=90°,AD∥BC,
∴∠GAE=90°,∠G=∠ECB,
∵E是AB边的中点,
∴AE=BE,
在△AGE和△BCE中,,
∴△AGE≌△BCE(AAS),
∴AG=BC,∠G=∠2,
∴AF+BC=AF+AG=FG,
∵∠1=∠2+∠G=2∠2,
∴∠2=∠G,
∴FG=CF=5,
∴AF+BC=5.
24.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC且AD=BC,
∵BE=CF,
∴BC=EF,
∴AD=EF,
∵AD∥EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴四边形AEFD是矩形;
(2)解:∵四边形ABCD是菱形,AD=10,
∴AD=AB=BC=10,
∵EC=4,
∴BE=10﹣4=6,
在Rt△ABE中,AE=,
在Rt△AEC中,AC=,
∵四边形ABCD是菱形,
∴OA=OC,
∴OE=AC=
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
