2020-2021学年八年级数学青岛版下册《6.3特殊平行四边形—菱形》同步提升训练(word版、含解析)
文档属性
| 名称 | 2020-2021学年八年级数学青岛版下册《6.3特殊平行四边形—菱形》同步提升训练(word版、含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 425.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 18:02:27 | ||
图片预览


文档简介
青岛版2021年度八年级数学下册《6.3特殊平行四边形—菱形》同步提升训练(附答案)
一、选择题
1.如图,在?ABCD中,AB=BC=5.对角线BD=8,则?ABCD的面积为( )
A.20
B.24
C.40
D.48
2.如图,在△ABC中,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F,若AF=8,则四边形AEDF的周长是( )
A.24
B.28
C.32
D.36
3.下列对菱形的描述错误的是( )
A.菱形的四条边都相等
B.对角线相等的平行四边形是菱形
C.菱形的对角线互相垂直
D.邻边相等的平行四边形是菱形
4.如图平行四边形ABCD中,∠A=110°,AD=DC.E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )
A.35°
B.45°
C.50°
D.55°
5.如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列条件能判定四边形AEDF是菱形的是( )
A.AD⊥BC
B.AD为BC边上的中线
C.AD=BD
D.AD平分∠BAC
6.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )
A.10
B.12
C.16
D.18
7.将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1
B.2
C.2
D.4
8.如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )
A.100°
B.105°
C.110°
D.120°
9.两张全等的矩形纸片ABCD,AECF按如图方式交叉叠放在一起,AB=AF,AE=BC.若AB=2,BC=6,则图中阴影部分的面积为( )
A.4
B.
C.
D.6
二、填空题
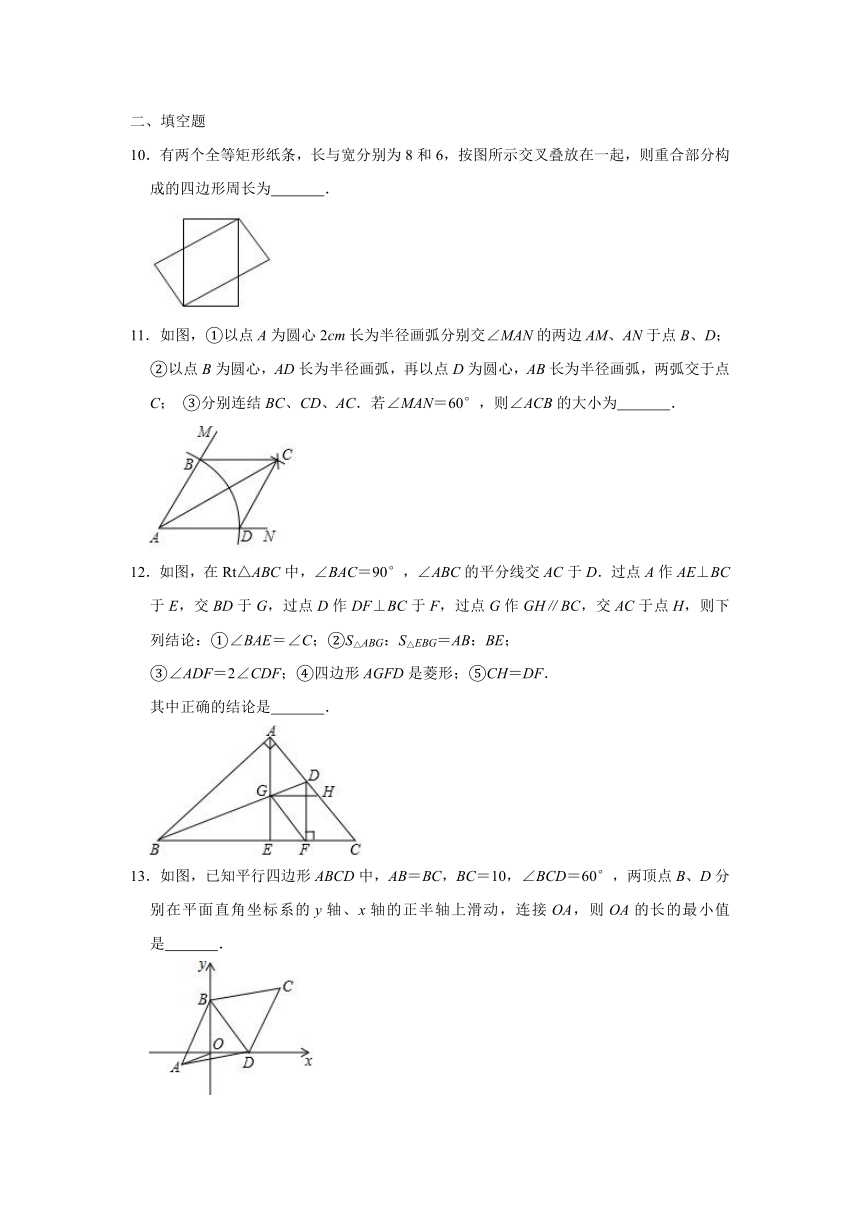
10.有两个全等矩形纸条,长与宽分别为8和6,按图所示交叉叠放在一起,则重合部分构成的四边形周长为
.
11.如图,①以点A为圆心2cm长为半径画弧分别交∠MAN的两边AM、AN于点B、D;②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;
③分别连结BC、CD、AC.若∠MAN=60°,则∠ACB的大小为
.
12.如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线交AC于D.过点A作AE⊥BC于E,交BD于G,过点D作DF⊥BC于F,过点G作GH∥BC,交AC于点H,则下列结论:①∠BAE=∠C;②S△ABG:S△EBG=AB:BE;
③∠ADF=2∠CDF;④四边形AGFD是菱形;⑤CH=DF.
其中正确的结论是
.
13.如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是
.
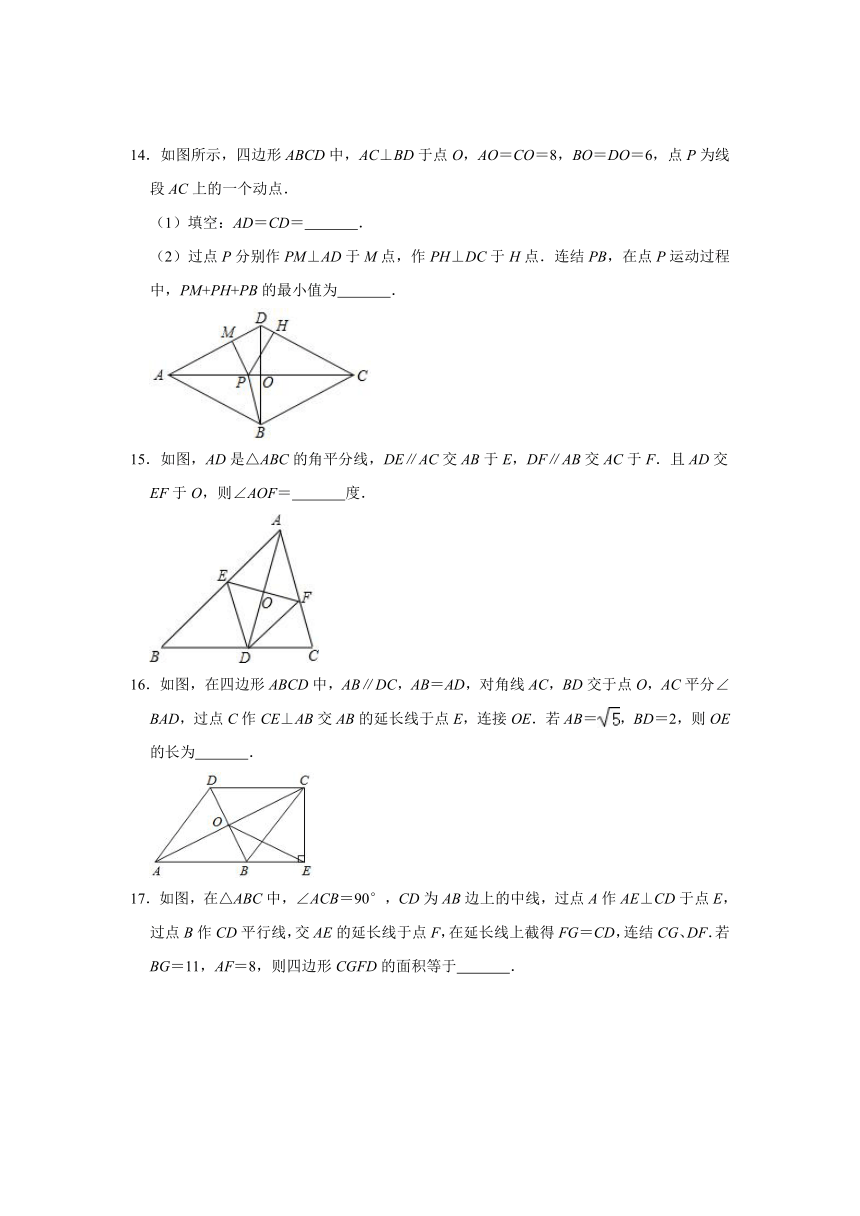
14.如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点.
(1)填空:AD=CD=
.
(2)过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连结PB,在点P运动过程中,PM+PH+PB的最小值为
.
15.如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF=
度.
16.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.若AB=,BD=2,则OE的长为
.
17.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD于点E,过点B作CD平行线,交AE的延长线于点F,在延长线上截得FG=CD,连结CG、DF.若BG=11,AF=8,则四边形CGFD的面积等于
.
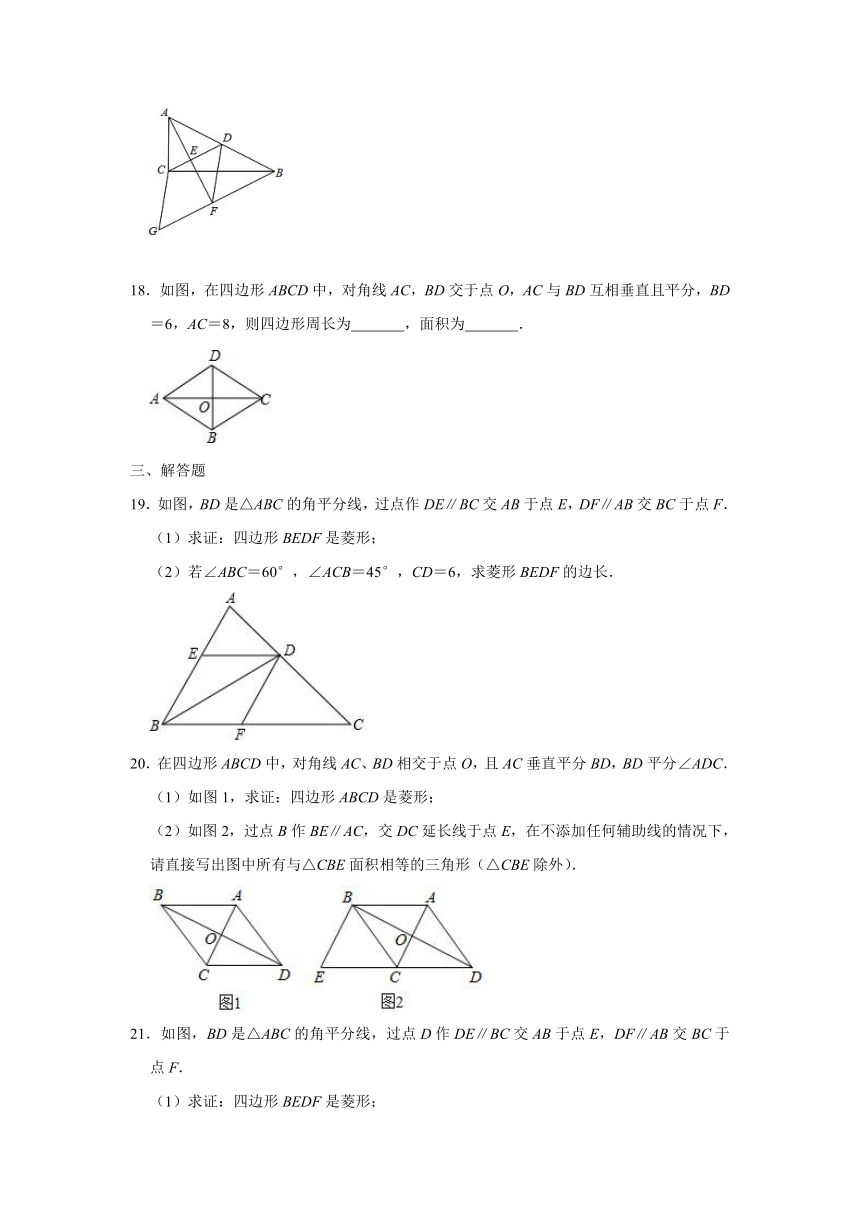
18.如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=6,AC=8,则四边形周长为
,面积为
.
三、解答题
19.如图,BD是△ABC的角平分线,过点作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.
20.在四边形ABCD中,对角线AC、BD相交于点O,且AC垂直平分BD,BD平分∠ADC.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,过点B作BE∥AC,交DC延长线于点E,在不添加任何辅助线的情况下,请直接写出图中所有与△CBE面积相等的三角形(△CBE除外).
21.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.
22.如图,在?ABCD中,EF是对角线AC的垂直平分线,分别与AD,BC交于点E,F.
(1)求证:四边形AECF是菱形;
(2)若AC=6,AE=5,求菱形AECF的面积.
23.如图,在?ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、DA的中点.
(1)求证:四边形AECF是菱形;
(2)若AB=2,求BD的长.
24.已知,在平行四边形ABCD中,点F是AB上一点,连接DF交对角线AC于E,连接BE.
(1)如图1,若∠EBC=∠EFA,EC平分∠DEB,求证:平行四边形ABCD是菱形;
(2)如图2,对角线AC与BD相交于点O,当点F是AB的中点时,直接写出与△ADF面积相等的三角形(不包括以AD为边的三角形).
25.如图,AM∥BN,C是BN上一点,AB=BC,BD平分∠ABN,分别交AC,AM于点O,D,DE⊥BD,交BN于点E.
(1)求证:△ADO≌△CBO;
(2)求证:四边形ABCD是菱形;
(3)若DE=AB=2,求菱形ABCD的面积.
26.如图1,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.
参考答案
1.解:如图所示,连接AC交BD于O,
在?ABCD中,AB=BC=5,
∴四边形ABCD是菱形,
∴AC⊥BD,
又∵对角线BD=8,
∴BO=4,
在Rt△AOB中,AO===3,
∴AC=2AO=6,
∴菱形ABCD的面积为==24.
故选:B.
2.解:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,∠EAD=∠FDA,
∵AD平分∠BAC,
∴∠EAD=∠FAD=∠FDA,
∴FA=FD,
∴平行四边形AEDF为菱形.
∵AF=8,
∴C菱形AEDF=4AF=4×8=32.
故选:C.
3.解:A、∵菱形的四条边都相等,
∴选项A不符合题意;
B、∵对角线相等的平行四边形是矩形,
∴选项B符合题意;
C、∵菱形的对角线互相垂直平分,
∴选项C不符合题意;
D、∵邻边相等的平行四边形形是菱形,
∴选项D不符合题意;
故选:B.
4.解:∵平行四边形ABCD中,AD=DC,
∴四边形ABCD为菱形,
∴AB=BC,∠ABC=180°﹣∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=55°,
∵PE⊥AB,
∴∠PEB=90°
∴∠PEF=90°﹣55°=35°,
故选:A.
5.解:添加AD平分∠BAC可判定四边形AEDF是菱形,
理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠DAC=∠ADE,
∴∠DAB=∠ADE,
∴AE=DE,
∴平行四边形AEDF是菱形,
故选:D.
6.解:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF=BF=6,
∴OA===8,
∴AE=2OA=16;
故选:C.
7.解:∵四边形AECF是菱形,AB=3,
∴假设BE=x,则AE=3﹣x,CE=3﹣x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
2BE=CE,
∴CE=2x,
∴2x=3﹣x,
解得:x=1,
∴CE=2,利用勾股定理得出:
BC2+BE2=EC2,
BC===,
又∵AE=AB﹣BE=3﹣1=2,
则菱形的面积是:AE?BC=2.
故选:C.
8.解:∵四边形ABCD的四边都相等,
∴四边形ABCD是菱形,
∴∠B=∠D,∠DAB=∠C,AD∥BC,
∴∠DAB+∠B=180°,
∵△AMN是等边三角形,AM=AB,
∴∠AMN=∠ANM=60°,AM=AD,
∴∠B=∠AMB,∠D=∠AND,
由三角形的内角和定理得:∠BAM=∠NAD,
设∠BAM=∠NAD=x,
则∠D=∠AND=180°﹣60°﹣2x,
∵∠NAD+∠D+∠AND=180°,
∴x+2(180°﹣60°﹣2x)=180°,
解得:x=20°,
∴∠C=∠BAD=2×20°+60°=100°.
故选:A.
9.解:如图所示:
∵两张全等的矩形纸片ABCD,AECF按如图方式交叉叠放在一起,
∴AD∥BC,AE∥CF,∠B=∠BAD=∠EAF=∠F=90°,AD=BC=6,
∴四边形AHCG是平行四边形,∠BAH=∠FAG,
在△AFG和△ABH中,
,
∴△AFG≌△ABH(ASA),
∴AG=AH,
∴平行四边形AHCG是菱形,
∴AH=CH,
设AH=CH=x,则BH=6﹣x,
在Rt△ABH中,由勾股定理得:22+(6﹣x)2=x2,
解得:x=,
∴BH=6﹣=,
∴图中阴影部分的面积=BH×AB=××2=,
故选:B.
10.解:如图所示:
由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=6,AD∥BC,BF∥DE,AD=8,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH=DG=BG,
设BH=DH=x,则AH=8﹣x,
在Rt△ABH中,由勾股定理得:62+(8﹣x)2=x2,
解得:x=,
∴BG=,
∴四边形BGDH的周长=4BG=25;
故答案为:25.
11.解:由题意可得:AB=BC=CD=AD=2cm,
∴四边形ABCD是菱形,
∴BC∥DA,∠CAB=∠CAD=∠MAN=30°,
∴∠ACB=∠CAD=30°,
故答案为:30°.
12.解:①∵∠BAC=90°,
∴∠BAE+∠CAE=90°,
∵AE⊥BC,
∴∠C+∠CAE=90°,
∴∠BAE=∠C,①正确;
②作AM∥BD交CB的延长线于M,如图所示:
则∠M=∠CBD,∠BAM=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠M=∠BAM,
∴AB=BM,
∵AM∥BD,
∴AG:GE=BM:BE,
∴AG:GE=AB:BE,
∵S△ABG:S△EBG=AG:GE,
∴S△ABG:S△EBG=AB:BE;②正确;
④∵∠AGD=∠ABD+∠BAE,∠ADG=∠CBD+∠C,∠BAE=∠C,∠CBD=∠ABD,
∴∠AGD=∠ADG,
∴AG=AD,
∵∠BAC=90°,BD平分∠ABC.DF⊥BC,
∴AD=DF,
∴AG=DF,
∵AE⊥BC,
∴AG∥DF,
∴四边形AGFD是平行四边形,
又∵AG=AD,
∴四边形AGFD是菱形;④正确;
⑤∵四边形AGFD是菱形;
∴∠AGD=∠FGD,GF=DF,∠ADB=∠FDB,
∴∠AGB=∠FGB,
在△ABG和△FBG中,,
∴△ABG≌△FBG(AAS),
∴∠BAE=∠BFG,
∵∠BAE=∠C,
∴∠BFG=∠C,
∴GF∥CH,
∵GH∥BC,
∴四边形GFCH是平行四边形,
∴GF=CH,
∴CH=DF,⑤正确;
③∵∠ADF=2∠ADB,
当∠C=30°,∠CDF=60°,
则∠ADF=120°,
∴∠ADF=2∠CDF;③不正确;
故答案为:①②④⑤.
13.解:如图所示:过点A作AE⊥BD于点E,
当点A,O,E在一条直线上,此时AO最短,
∵平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,
∴AB=AD=CD=BC=10,∠BAD=∠BCD=60°,
∴△ABD是等边三角形,
∴AE过点O,E为BD中点,
∵∠BOD=90°,BD=10,
∴EO=5,
故AO的最小值为:AO=AE﹣EO=ABsin60°﹣×BD=5﹣5.
故答案为:5﹣5.
14.解:(1)∵AC⊥BD于点O,
∴△AOD为直角三角形.
∴AD===10.
∵AC⊥BD于点O,AO=CO,
∴CD=AD=10.
故答案为:10;
(2)如图1所示:连接PD.
∵S△ADP+S△CDP=S△ADC,
∴AD?PM+DC?PH=AC?OD,即×10×PM+×10×PH=×16×6.
∴10×(PM+PH)=16×6.
∴PM+PH==,
∴当PB最短时,PM+PH+PB有最小值,
∵由垂线段最短可知:当BP⊥AC时,PB最短.
∴当点P与点O重合时,PM+PH+PB有最小,最小值=+6=.
故答案为:10,.
15.解:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,
∴OA=OD,OE=OF,∠2=∠3,
∵AD是△ABC的角平分线,
∵∠1=∠2,
∴∠1=∠3,
∴AE=DE.
∴?AEDF为菱形.
∴AD⊥EF,即∠AOF=90°.
故答案为:90.
16.解:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA===2,
∴OE=OA=2,
故答案为:2.
17.解:∵∠ACB=90°,CD为AB边上的中线,
∴AD=BD=CD,
∵BG∥CD,
∴AF⊥BG,
∴AD=BD=DF,
∴DF=CD,
∵FG=CD,
∴四边形CGFD为菱形,
∵CD∥BF,D为AB中点,
∴E为AF的中点,
∴EF=AF=4,
设GF=x,则BF=11﹣x,AB=2x,
∵在Rt△ABF中,∠BFA=90°,
∴AF2+BF2=AB2,即(11﹣x)2+82=(2x)2,
解得:x=5或x=﹣(舍去),
∴菱形CGFD的面积为:5×4=20,
故答案为:20.
18.解:∵AC与BD互相垂直且平分,
∴AD=AB=BC=CD,
∴四边形ABCD是菱形,
∵BD=6,AC=8,
∴OA=AC=4,OB=BD=3,
∴AB==5,
∴四边形周长为:20,面积为:×6×8=24.
故答案为:20,24.
19.证明:(1)∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF=∠ABC,
∴∠ABD=∠EDB,
∴DE=BE,
又∵四边形BEDF为平行四边形,
∴四边形BEDF是菱形;
(2)如图,过点D作DH⊥BC于H,
∵DF∥AB,
∴∠ABC=∠DFC=60°,
∵DH⊥BC,
∴∠FDH=30°,
∴FH=DF,DH=FH=DF,
∵∠C=45°,DH⊥BC,
∴∠C=∠HDC=45°,
∴DC=DH=DF=6,
∴DF=2,
∴菱形BEDF的边长为2.
20.(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=CD,
∵BD平分∠ADC,
∴∠ADO=∠CDO,
又OD=OD,∠AOD=∠COD,
∴△AOD≌△COD(ASA),
∴AD=CD,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴AB∥CD,
∵BE∥CE,
∴四边形ACEB是平行四边形,
∴DC=AB=CE,
∴图中所有与△CBE面积相等的三角形有△BCD,△ABD,△ACD,△ABC.
21.(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=80°,∠C=30°,
∴∠ABC=180°﹣80°﹣30°=70°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=70°,
∴∠BDE=∠EDF=35°.
22.证明:(1)∵对角线AC的垂直平分线EF分别与AC、BC、AD交于点O、E、F,
∴AF=CF,AE=CE,OA=OC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠FCA,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AF=CF,AE=CE,
∴AE=EC=CF=AF,
∴四边形AECF为菱形;
(2)∵四边形AECF是菱形,
∴AC⊥EF,OA=OC,OE=OF,
∵AC=6,AE=5,
∴OE=3,
由勾股定理可得:OE=,
∴EF=2OE=8,
∴菱形AECF的面积=.
23.(1)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∵E,F分别是BC,AD的中点
∴BE=CE=BC,AF=AD,
∴CE=AF,CE∥AF,
∴四边形AECF是平行四边形,
∵BC=2AB,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AE=BE=CE,
∴平行四边形AECF是菱形;
(2)解:作BG⊥AD于G,如图所示:
则∠ABG=90°﹣∠ABC=30°,
∴AG=AB=1,BG=AG=,
∵AD=BC=2AB=4,
∴DG=AG+AD=5,
∴BD===2.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EDC=∠EFA,
∵∠EBC=∠EFA,
∴∠EBC=∠EDC,
∵EC平分∠DEB,
∴∠DCE=∠BCE,
在△CED和△CEB中,,
∴△CED≌△CEB(AAS),
∴CD=CB,
∵四边形ABCD为平行四边形,
∴平行四边形ABCD为菱形;
(2)解:与△ADF面积相等的三角形(不包括以AD为边的三角形)为△AOB、△BOC、△COD、△DFB;理由如下:
∵四边形ABCD是平行四边形,
∴OA=OB,OC=OD,
∴△AOB的面积=△BOC的面积=△COD的面积=△ABD的面积,
∵点F是AB的中点,
∴△ADF的面积=△DFB的面积=△ABD的面积,
∴△AOB的面积=△BOC的面积=△COD的面积=△DFB的面积=△ADF的面积.
25.(1)证明:∵AB=BC,BD平分∠ABN,
∴AO=CO.
∵AM∥BN,
∴∠DAC=∠ACB.
在△ADO和△CBD中,,
∴△ADO≌△CBO(ASA);
(2)证明:由(1)得△ADO≌△CBD.
∴AD=CB.
又∵AM∥BN,
∴四边形ABCD是平行四边形.
∵AB=BC,
∴四边形ABCD是菱形;
(3)解:由(2)得四边形ABCD是菱形.
∴AC⊥BD,OB=OD.
又∵DE⊥BD,
∴AC∥DE.
又∵AM∥BN,
∴四边形ACED平行四边形.
∴AC=DE=2.
∴AO=1.
在Rt△AOB中,由勾股定理得:BO===,
∴BD=2BO=2.
∴S菱形ABCD=AC?BD=×2×2=2.
26.(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是平行四边形,
∴DC=AB.
∵OE=CD,
∴OE=AB.
∴平行四边形AEBO是矩形,
∴∠BOA=90°.
∴AC⊥BD.
∴平行四边形ABCD是菱形;
(2)解:由(1)得:四边形AEBO是矩形,四边形ABCD是菱形,
∴OA=BE=2,AC⊥BD,BO=DO,∠ADO=30°,
∴OD=OA=2,
∴BD=2OD=4.
一、选择题
1.如图,在?ABCD中,AB=BC=5.对角线BD=8,则?ABCD的面积为( )
A.20
B.24
C.40
D.48
2.如图,在△ABC中,AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F,若AF=8,则四边形AEDF的周长是( )
A.24
B.28
C.32
D.36
3.下列对菱形的描述错误的是( )
A.菱形的四条边都相等
B.对角线相等的平行四边形是菱形
C.菱形的对角线互相垂直
D.邻边相等的平行四边形是菱形
4.如图平行四边形ABCD中,∠A=110°,AD=DC.E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PEF=( )
A.35°
B.45°
C.50°
D.55°
5.如图,在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列条件能判定四边形AEDF是菱形的是( )
A.AD⊥BC
B.AD为BC边上的中线
C.AD=BD
D.AD平分∠BAC
6.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )
A.10
B.12
C.16
D.18
7.将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1
B.2
C.2
D.4
8.如图,已知四边形ABCD的四边相等,等边△AMN的顶点M、N分别在BC、CD上,且AM=AB,则∠C为( )
A.100°
B.105°
C.110°
D.120°
9.两张全等的矩形纸片ABCD,AECF按如图方式交叉叠放在一起,AB=AF,AE=BC.若AB=2,BC=6,则图中阴影部分的面积为( )
A.4
B.
C.
D.6
二、填空题
10.有两个全等矩形纸条,长与宽分别为8和6,按图所示交叉叠放在一起,则重合部分构成的四边形周长为
.
11.如图,①以点A为圆心2cm长为半径画弧分别交∠MAN的两边AM、AN于点B、D;②以点B为圆心,AD长为半径画弧,再以点D为圆心,AB长为半径画弧,两弧交于点C;
③分别连结BC、CD、AC.若∠MAN=60°,则∠ACB的大小为
.
12.如图,在Rt△ABC中,∠BAC=90°,∠ABC的平分线交AC于D.过点A作AE⊥BC于E,交BD于G,过点D作DF⊥BC于F,过点G作GH∥BC,交AC于点H,则下列结论:①∠BAE=∠C;②S△ABG:S△EBG=AB:BE;
③∠ADF=2∠CDF;④四边形AGFD是菱形;⑤CH=DF.
其中正确的结论是
.
13.如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是
.
14.如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点.
(1)填空:AD=CD=
.
(2)过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连结PB,在点P运动过程中,PM+PH+PB的最小值为
.
15.如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF=
度.
16.如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.若AB=,BD=2,则OE的长为
.
17.如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD于点E,过点B作CD平行线,交AE的延长线于点F,在延长线上截得FG=CD,连结CG、DF.若BG=11,AF=8,则四边形CGFD的面积等于
.
18.如图,在四边形ABCD中,对角线AC,BD交于点O,AC与BD互相垂直且平分,BD=6,AC=8,则四边形周长为
,面积为
.
三、解答题
19.如图,BD是△ABC的角平分线,过点作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)若∠ABC=60°,∠ACB=45°,CD=6,求菱形BEDF的边长.
20.在四边形ABCD中,对角线AC、BD相交于点O,且AC垂直平分BD,BD平分∠ADC.
(1)如图1,求证:四边形ABCD是菱形;
(2)如图2,过点B作BE∥AC,交DC延长线于点E,在不添加任何辅助线的情况下,请直接写出图中所有与△CBE面积相等的三角形(△CBE除外).
21.如图,BD是△ABC的角平分线,过点D作DE∥BC交AB于点E,DF∥AB交BC于点F.
(1)求证:四边形BEDF是菱形;
(2)如果∠A=80°,∠C=30°,求∠BDE的度数.
22.如图,在?ABCD中,EF是对角线AC的垂直平分线,分别与AD,BC交于点E,F.
(1)求证:四边形AECF是菱形;
(2)若AC=6,AE=5,求菱形AECF的面积.
23.如图,在?ABCD中,∠ABC=60°,BC=2AB,点E、F分别是BC、DA的中点.
(1)求证:四边形AECF是菱形;
(2)若AB=2,求BD的长.
24.已知,在平行四边形ABCD中,点F是AB上一点,连接DF交对角线AC于E,连接BE.
(1)如图1,若∠EBC=∠EFA,EC平分∠DEB,求证:平行四边形ABCD是菱形;
(2)如图2,对角线AC与BD相交于点O,当点F是AB的中点时,直接写出与△ADF面积相等的三角形(不包括以AD为边的三角形).
25.如图,AM∥BN,C是BN上一点,AB=BC,BD平分∠ABN,分别交AC,AM于点O,D,DE⊥BD,交BN于点E.
(1)求证:△ADO≌△CBO;
(2)求证:四边形ABCD是菱形;
(3)若DE=AB=2,求菱形ABCD的面积.
26.如图1,?ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.
(1)求证:四边形ABCD是菱形;
(2)若∠ADC=60°,BE=2,求BD的长.
参考答案
1.解:如图所示,连接AC交BD于O,
在?ABCD中,AB=BC=5,
∴四边形ABCD是菱形,
∴AC⊥BD,
又∵对角线BD=8,
∴BO=4,
在Rt△AOB中,AO===3,
∴AC=2AO=6,
∴菱形ABCD的面积为==24.
故选:B.
2.解:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,∠EAD=∠FDA,
∵AD平分∠BAC,
∴∠EAD=∠FAD=∠FDA,
∴FA=FD,
∴平行四边形AEDF为菱形.
∵AF=8,
∴C菱形AEDF=4AF=4×8=32.
故选:C.
3.解:A、∵菱形的四条边都相等,
∴选项A不符合题意;
B、∵对角线相等的平行四边形是矩形,
∴选项B符合题意;
C、∵菱形的对角线互相垂直平分,
∴选项C不符合题意;
D、∵邻边相等的平行四边形形是菱形,
∴选项D不符合题意;
故选:B.
4.解:∵平行四边形ABCD中,AD=DC,
∴四边形ABCD为菱形,
∴AB=BC,∠ABC=180°﹣∠A=70°,
∵E,F分别为AB,BC的中点,
∴BE=BF,∠BEF=∠BFE=55°,
∵PE⊥AB,
∴∠PEB=90°
∴∠PEF=90°﹣55°=35°,
故选:A.
5.解:添加AD平分∠BAC可判定四边形AEDF是菱形,
理由如下:
∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠DAC=∠ADE,
∴∠DAB=∠ADE,
∴AE=DE,
∴平行四边形AEDF是菱形,
故选:D.
6.解:如图所示:
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,
∴∠DAE=∠BEA,
∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,
∴AF=BE,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF=BF=6,
∴OA===8,
∴AE=2OA=16;
故选:C.
7.解:∵四边形AECF是菱形,AB=3,
∴假设BE=x,则AE=3﹣x,CE=3﹣x,
∵四边形AECF是菱形,
∴∠FCO=∠ECO,
∵∠ECO=∠ECB,
∴∠ECO=∠ECB=∠FCO=30°,
2BE=CE,
∴CE=2x,
∴2x=3﹣x,
解得:x=1,
∴CE=2,利用勾股定理得出:
BC2+BE2=EC2,
BC===,
又∵AE=AB﹣BE=3﹣1=2,
则菱形的面积是:AE?BC=2.
故选:C.
8.解:∵四边形ABCD的四边都相等,
∴四边形ABCD是菱形,
∴∠B=∠D,∠DAB=∠C,AD∥BC,
∴∠DAB+∠B=180°,
∵△AMN是等边三角形,AM=AB,
∴∠AMN=∠ANM=60°,AM=AD,
∴∠B=∠AMB,∠D=∠AND,
由三角形的内角和定理得:∠BAM=∠NAD,
设∠BAM=∠NAD=x,
则∠D=∠AND=180°﹣60°﹣2x,
∵∠NAD+∠D+∠AND=180°,
∴x+2(180°﹣60°﹣2x)=180°,
解得:x=20°,
∴∠C=∠BAD=2×20°+60°=100°.
故选:A.
9.解:如图所示:
∵两张全等的矩形纸片ABCD,AECF按如图方式交叉叠放在一起,
∴AD∥BC,AE∥CF,∠B=∠BAD=∠EAF=∠F=90°,AD=BC=6,
∴四边形AHCG是平行四边形,∠BAH=∠FAG,
在△AFG和△ABH中,
,
∴△AFG≌△ABH(ASA),
∴AG=AH,
∴平行四边形AHCG是菱形,
∴AH=CH,
设AH=CH=x,则BH=6﹣x,
在Rt△ABH中,由勾股定理得:22+(6﹣x)2=x2,
解得:x=,
∴BH=6﹣=,
∴图中阴影部分的面积=BH×AB=××2=,
故选:B.
10.解:如图所示:
由题意得:矩形ABCD≌矩形BEDF,
∴∠A=90°,AB=BE=6,AD∥BC,BF∥DE,AD=8,
∴四边形BGDH是平行四边形,
∴平行四边形BGDH的面积=BG×AB=BH×BE,
∴BG=BH,
∴四边形BGDH是菱形,
∴BH=DH=DG=BG,
设BH=DH=x,则AH=8﹣x,
在Rt△ABH中,由勾股定理得:62+(8﹣x)2=x2,
解得:x=,
∴BG=,
∴四边形BGDH的周长=4BG=25;
故答案为:25.
11.解:由题意可得:AB=BC=CD=AD=2cm,
∴四边形ABCD是菱形,
∴BC∥DA,∠CAB=∠CAD=∠MAN=30°,
∴∠ACB=∠CAD=30°,
故答案为:30°.
12.解:①∵∠BAC=90°,
∴∠BAE+∠CAE=90°,
∵AE⊥BC,
∴∠C+∠CAE=90°,
∴∠BAE=∠C,①正确;
②作AM∥BD交CB的延长线于M,如图所示:
则∠M=∠CBD,∠BAM=∠ABD,
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∴∠M=∠BAM,
∴AB=BM,
∵AM∥BD,
∴AG:GE=BM:BE,
∴AG:GE=AB:BE,
∵S△ABG:S△EBG=AG:GE,
∴S△ABG:S△EBG=AB:BE;②正确;
④∵∠AGD=∠ABD+∠BAE,∠ADG=∠CBD+∠C,∠BAE=∠C,∠CBD=∠ABD,
∴∠AGD=∠ADG,
∴AG=AD,
∵∠BAC=90°,BD平分∠ABC.DF⊥BC,
∴AD=DF,
∴AG=DF,
∵AE⊥BC,
∴AG∥DF,
∴四边形AGFD是平行四边形,
又∵AG=AD,
∴四边形AGFD是菱形;④正确;
⑤∵四边形AGFD是菱形;
∴∠AGD=∠FGD,GF=DF,∠ADB=∠FDB,
∴∠AGB=∠FGB,
在△ABG和△FBG中,,
∴△ABG≌△FBG(AAS),
∴∠BAE=∠BFG,
∵∠BAE=∠C,
∴∠BFG=∠C,
∴GF∥CH,
∵GH∥BC,
∴四边形GFCH是平行四边形,
∴GF=CH,
∴CH=DF,⑤正确;
③∵∠ADF=2∠ADB,
当∠C=30°,∠CDF=60°,
则∠ADF=120°,
∴∠ADF=2∠CDF;③不正确;
故答案为:①②④⑤.
13.解:如图所示:过点A作AE⊥BD于点E,
当点A,O,E在一条直线上,此时AO最短,
∵平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,
∴AB=AD=CD=BC=10,∠BAD=∠BCD=60°,
∴△ABD是等边三角形,
∴AE过点O,E为BD中点,
∵∠BOD=90°,BD=10,
∴EO=5,
故AO的最小值为:AO=AE﹣EO=ABsin60°﹣×BD=5﹣5.
故答案为:5﹣5.
14.解:(1)∵AC⊥BD于点O,
∴△AOD为直角三角形.
∴AD===10.
∵AC⊥BD于点O,AO=CO,
∴CD=AD=10.
故答案为:10;
(2)如图1所示:连接PD.
∵S△ADP+S△CDP=S△ADC,
∴AD?PM+DC?PH=AC?OD,即×10×PM+×10×PH=×16×6.
∴10×(PM+PH)=16×6.
∴PM+PH==,
∴当PB最短时,PM+PH+PB有最小值,
∵由垂线段最短可知:当BP⊥AC时,PB最短.
∴当点P与点O重合时,PM+PH+PB有最小,最小值=+6=.
故答案为:10,.
15.解:∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形,
∴OA=OD,OE=OF,∠2=∠3,
∵AD是△ABC的角平分线,
∵∠1=∠2,
∴∠1=∠3,
∴AE=DE.
∴?AEDF为菱形.
∴AD⊥EF,即∠AOF=90°.
故答案为:90.
16.解:∵AB∥CD,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴?ABCD是菱形;
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴OB=BD=1,
在Rt△AOB中,AB=,OB=1,
∴OA===2,
∴OE=OA=2,
故答案为:2.
17.解:∵∠ACB=90°,CD为AB边上的中线,
∴AD=BD=CD,
∵BG∥CD,
∴AF⊥BG,
∴AD=BD=DF,
∴DF=CD,
∵FG=CD,
∴四边形CGFD为菱形,
∵CD∥BF,D为AB中点,
∴E为AF的中点,
∴EF=AF=4,
设GF=x,则BF=11﹣x,AB=2x,
∵在Rt△ABF中,∠BFA=90°,
∴AF2+BF2=AB2,即(11﹣x)2+82=(2x)2,
解得:x=5或x=﹣(舍去),
∴菱形CGFD的面积为:5×4=20,
故答案为:20.
18.解:∵AC与BD互相垂直且平分,
∴AD=AB=BC=CD,
∴四边形ABCD是菱形,
∵BD=6,AC=8,
∴OA=AC=4,OB=BD=3,
∴AB==5,
∴四边形周长为:20,面积为:×6×8=24.
故答案为:20,24.
19.证明:(1)∵DE∥BC,DF∥AB,
∴四边形DEBF是平行四边形,
∵DE∥BC,
∴∠EDB=∠DBF,
∵BD平分∠ABC,
∴∠ABD=∠DBF=∠ABC,
∴∠ABD=∠EDB,
∴DE=BE,
又∵四边形BEDF为平行四边形,
∴四边形BEDF是菱形;
(2)如图,过点D作DH⊥BC于H,
∵DF∥AB,
∴∠ABC=∠DFC=60°,
∵DH⊥BC,
∴∠FDH=30°,
∴FH=DF,DH=FH=DF,
∵∠C=45°,DH⊥BC,
∴∠C=∠HDC=45°,
∴DC=DH=DF=6,
∴DF=2,
∴菱形BEDF的边长为2.
20.(1)证明:∵AC垂直平分BD,
∴AB=AD,BC=CD,
∵BD平分∠ADC,
∴∠ADO=∠CDO,
又OD=OD,∠AOD=∠COD,
∴△AOD≌△COD(ASA),
∴AD=CD,
∴AB=AD=CD=BC,
∴四边形ABCD是菱形.
(2)解:∵四边形ABCD是菱形,
∴AB∥CD,
∵BE∥CE,
∴四边形ACEB是平行四边形,
∴DC=AB=CE,
∴图中所有与△CBE面积相等的三角形有△BCD,△ABD,△ACD,△ABC.
21.(1)证明:∵DE∥BC,DF∥AB
∴四边形DEBF是平行四边形
∵DE∥BC
∴∠EDB=∠DBF
∵BD平分∠ABC
∴∠ABD=∠DBF=∠ABC
∴∠ABD=∠EDB
∴DE=BE且四边形BEDF为平行四边形
∴四边形BEDF为菱形;
(2)解:∵∠A=80°,∠C=30°,
∴∠ABC=180°﹣80°﹣30°=70°,
∵四边形BEDF为菱形,
∴∠EDF=∠ABC=70°,
∴∠BDE=∠EDF=35°.
22.证明:(1)∵对角线AC的垂直平分线EF分别与AC、BC、AD交于点O、E、F,
∴AF=CF,AE=CE,OA=OC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠FCA,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AF=CF,AE=CE,
∴AE=EC=CF=AF,
∴四边形AECF为菱形;
(2)∵四边形AECF是菱形,
∴AC⊥EF,OA=OC,OE=OF,
∵AC=6,AE=5,
∴OE=3,
由勾股定理可得:OE=,
∴EF=2OE=8,
∴菱形AECF的面积=.
23.(1)证明:∵四边形ABCD是平行四边形,
∴BC∥AD,BC=AD.
∵E,F分别是BC,AD的中点
∴BE=CE=BC,AF=AD,
∴CE=AF,CE∥AF,
∴四边形AECF是平行四边形,
∵BC=2AB,
∴AB=BE,
∵∠ABC=60°,
∴△ABE是等边三角形,
∴AE=BE=CE,
∴平行四边形AECF是菱形;
(2)解:作BG⊥AD于G,如图所示:
则∠ABG=90°﹣∠ABC=30°,
∴AG=AB=1,BG=AG=,
∵AD=BC=2AB=4,
∴DG=AG+AD=5,
∴BD===2.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠EDC=∠EFA,
∵∠EBC=∠EFA,
∴∠EBC=∠EDC,
∵EC平分∠DEB,
∴∠DCE=∠BCE,
在△CED和△CEB中,,
∴△CED≌△CEB(AAS),
∴CD=CB,
∵四边形ABCD为平行四边形,
∴平行四边形ABCD为菱形;
(2)解:与△ADF面积相等的三角形(不包括以AD为边的三角形)为△AOB、△BOC、△COD、△DFB;理由如下:
∵四边形ABCD是平行四边形,
∴OA=OB,OC=OD,
∴△AOB的面积=△BOC的面积=△COD的面积=△ABD的面积,
∵点F是AB的中点,
∴△ADF的面积=△DFB的面积=△ABD的面积,
∴△AOB的面积=△BOC的面积=△COD的面积=△DFB的面积=△ADF的面积.
25.(1)证明:∵AB=BC,BD平分∠ABN,
∴AO=CO.
∵AM∥BN,
∴∠DAC=∠ACB.
在△ADO和△CBD中,,
∴△ADO≌△CBO(ASA);
(2)证明:由(1)得△ADO≌△CBD.
∴AD=CB.
又∵AM∥BN,
∴四边形ABCD是平行四边形.
∵AB=BC,
∴四边形ABCD是菱形;
(3)解:由(2)得四边形ABCD是菱形.
∴AC⊥BD,OB=OD.
又∵DE⊥BD,
∴AC∥DE.
又∵AM∥BN,
∴四边形ACED平行四边形.
∴AC=DE=2.
∴AO=1.
在Rt△AOB中,由勾股定理得:BO===,
∴BD=2BO=2.
∴S菱形ABCD=AC?BD=×2×2=2.
26.(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是平行四边形,
∴DC=AB.
∵OE=CD,
∴OE=AB.
∴平行四边形AEBO是矩形,
∴∠BOA=90°.
∴AC⊥BD.
∴平行四边形ABCD是菱形;
(2)解:由(1)得:四边形AEBO是矩形,四边形ABCD是菱形,
∴OA=BE=2,AC⊥BD,BO=DO,∠ADO=30°,
∴OD=OA=2,
∴BD=2OD=4.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
