2021—2022学年湘教版八年级数学上册2.5 全等三角形及其性质练习题 (word版含答案)
文档属性
| 名称 | 2021—2022学年湘教版八年级数学上册2.5 全等三角形及其性质练习题 (word版含答案) | 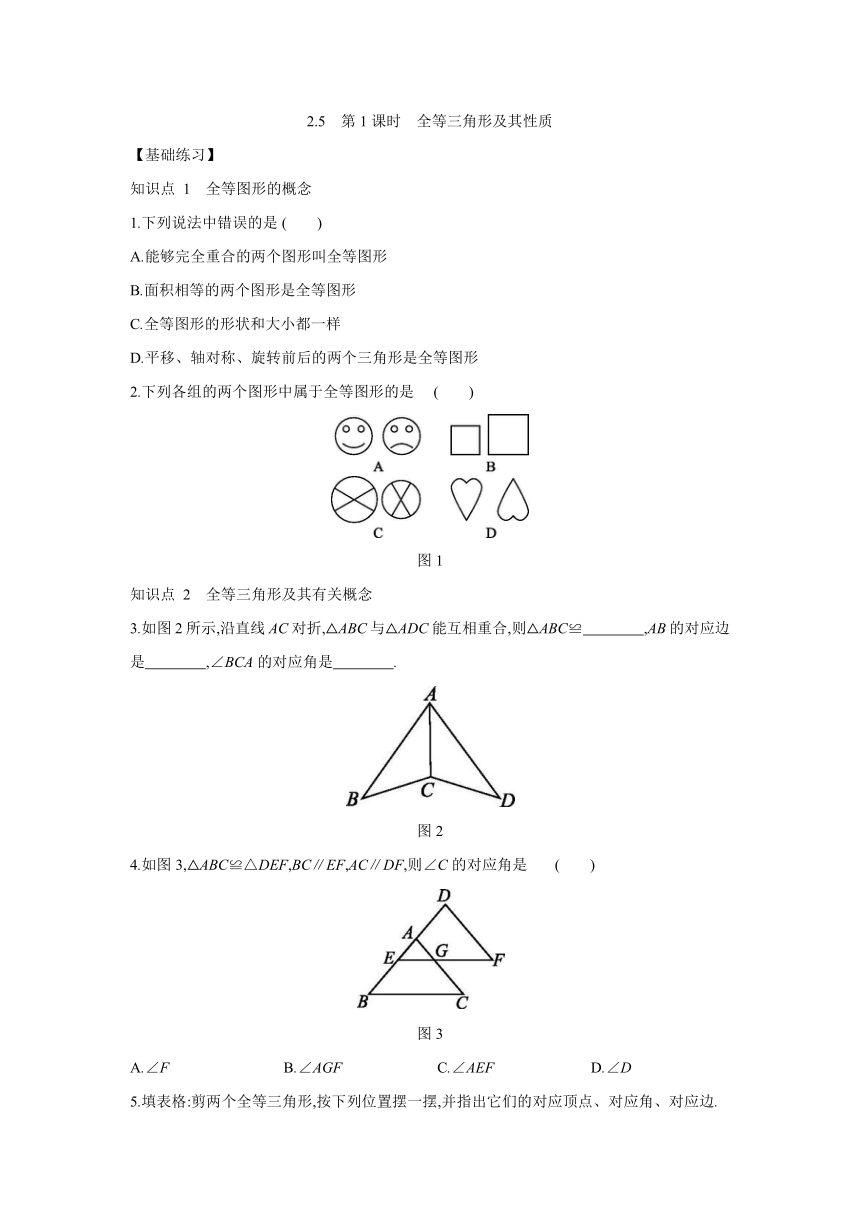 | |
| 格式 | docx | ||
| 文件大小 | 223.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 09:08:40 | ||
图片预览



文档简介
2.5 第1课时 全等三角形及其性质
【基础练习】
知识点
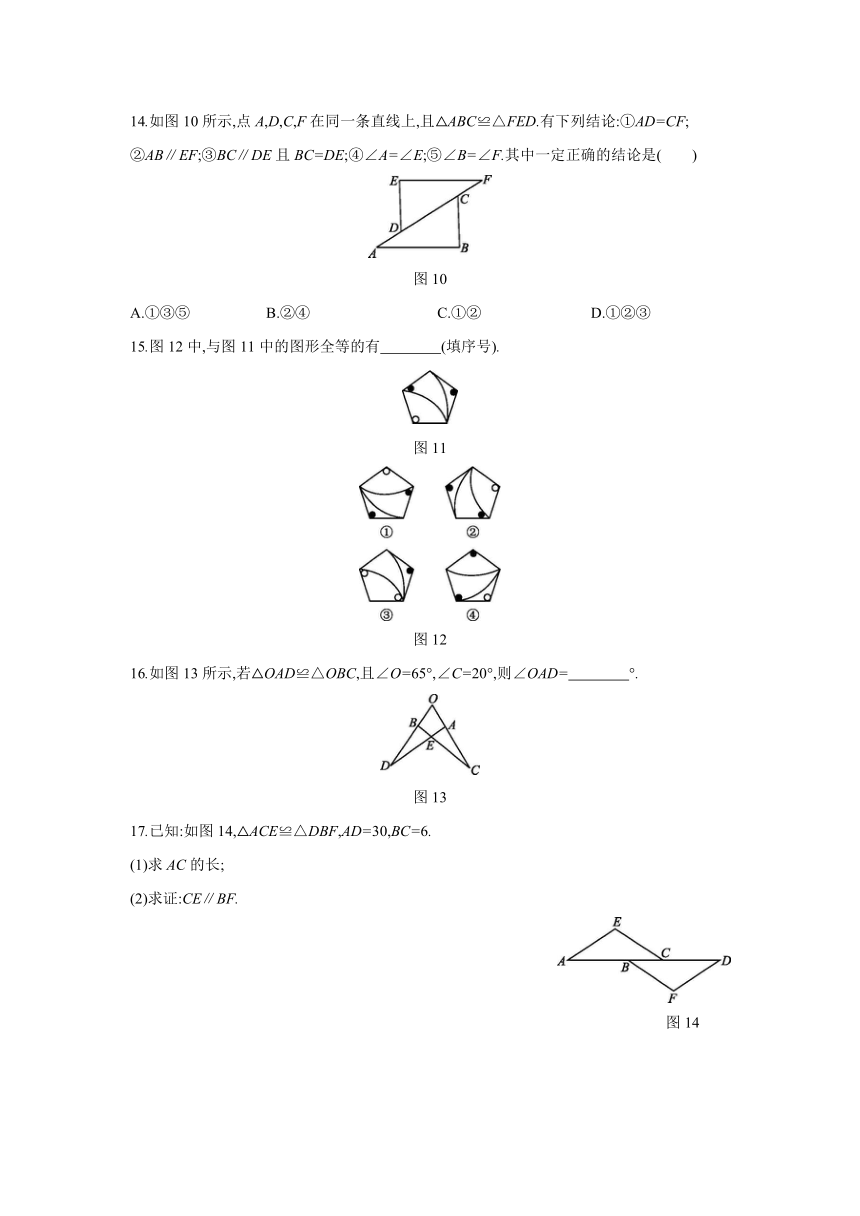
1 全等图形的概念
1.下列说法中错误的是
( )
A.能够完全重合的两个图形叫全等图形
B.面积相等的两个图形是全等图形
C.全等图形的形状和大小都一样
D.平移、轴对称、旋转前后的两个三角形是全等图形
2.下列各组的两个图形中属于全等图形的是
( )
图1
知识点
2 全等三角形及其有关概念
3.如图2所示,沿直线AC对折,△ABC与△ADC能互相重合,则△ABC≌ ,AB的对应边是 ,∠BCA的对应角是 .?
图2
4.如图3,△ABC≌△DEF,BC∥EF,AC∥DF,则∠C的对应角是
( )
图3
A.∠F
B.∠AGF
C.∠AEF
D.∠D
5.填表格:剪两个全等三角形,按下列位置摆一摆,并指出它们的对应顶点、对应角、对应边.
图形
对应顶点
对应角
对应边
知识点
3 全等三角形的性质
6.如图4,△ABC≌△CDA,AB=5,BC=7,AC=6,则AD边的长为
( )
图4
A.5
B.6
C.7
D.不确定
7.如图5,已知△ABC≌△ADC,∠B+∠D=160°,则∠B的度数是
( )
图5
A.80°
B.90°
C.100°
D.120°
8.[2020·淄博]
如图6,若△ABC≌△ADE,则下列结论中一定成立的是
( )
图6
A.AC=DE
B.∠BAD=∠CAE
C.AB=AE
D.∠ABC=∠AED
9.如图7所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为 .?
图7
10.已知△ABC≌△DEF,∠A=70°,∠E=30°,则∠F的度数为 .?
11.已知△ABC≌△DEF,∠A=80°,∠E-∠F=20°,求△DEF各内角的度数.
12.如图8所示,已知AB与CD相交于点O,△AOC≌△BOD.求证:AC∥BD.
图8
【能力提升】
13.如图9,△ABD≌△ACE,∠AEC=110°,则∠DAE的度数为
( )
图9
A.40°
B.30°
C.50°
D.60°
14.如图10所示,点A,D,C,F在同一条直线上,且△ABC≌△FED.有下列结论:①AD=CF;
②AB∥EF;③BC∥DE且BC=DE;④∠A=∠E;⑤∠B=∠F.其中一定正确的结论是( )
图10
A.①③⑤ B.②④
C.①②
D.①②③
15.图12中,与图11中的图形全等的有 (填序号).?
图11
图12
16.如图13所示,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= °.?
图13
17.已知:如图14,△ACE≌△DBF,AD=30,BC=6.
(1)求AC的长;
(2)求证:CE∥BF.
图14
18.如图15,△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,BC的延长线与AD交于点F,与DE交于点G,求∠DFB和∠DGB的度数.
图15
19.如图16所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠1∶∠2∶∠3=28∶5∶3,求∠α的度数.
图16
答案
1.B 2.D
3.△ADC AD ∠DCA
4.A [解析]
根据全等三角形对应角的定义可知∠C与∠F是对应角.
5.解:
图形
对应顶点
对应角
对应边
点A与点D,点B与点E,点C与点F
∠A与∠D,∠B与∠DEF,∠ACB与∠F
AB与DE,BC与EF,AC与DF
点A与点D,点B与点F,点C与点E
∠A与∠D,∠ABC与∠DFE,∠ACB与∠DEF
AB与DF,BC与FE,AC与DE
点A与点D,点B与点E,点C与点F
∠A与∠D,∠B与∠E,∠ACB与∠AFE
AB与DE,BC与EF,AC与DF
6.C [解析]
∵△ABC≌△CDA,∴AD=BC=7.故选C.
7.A [解析]
∵△ABC≌△ADC,∴∠B=∠D.又∵∠B+∠D=160°,∴∠B=80°.故选A.
8.B [解析]
∵△ABC≌△ADE,
∴AC=AE,AB=AD,∠ABC=∠ADE,∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
故A,C,D选项错误,B选项正确.
故选B.
9.2 [解析]
∵△ABE≌△ACF,
∴AC=AB=5,
∴EC=AC-AE=2.
故答案为2.
10.80° [解析]
∵△ABC≌△DEF,∴∠D=∠A=70°,∴∠F=180°-∠D-∠E=180°-70°-30°=80°.
11.解:∵△ABC≌△DEF,
∴∠D=∠A=80°,∴∠E+∠F=100°.
又∵∠E-∠F=20°,
∴∠E=60°,∠F=40°.
即∠D=80°,∠E=60°,∠F=40°.
12.证明:∵△AOC≌△BOD,
∴∠A=∠B(全等三角形的对应角相等),
∴AC∥BD(内错角相等,两直线平行).
13.A [解析]
∵∠AEC=110°,∴∠AED=180°-∠AEC=180°-110°=70°.∵△ABD≌△ACE,
∴AD=AE,∴∠AED=∠ADE,∴∠DAE=180°-2×70°=180°-140°=40°.
14.D [解析]
∵△ABC≌△FED,∴①AC=FD,∴AD=AC-CD=FD-CD=CF,结论①正确;
②∠A=∠F,∴AB∥EF,结论②正确;
③∠ACB=∠FDE,∴BC∥DE,又BC=DE,∴结论③正确;
④∠A=∠F,∠A不一定与∠E相等,结论④不一定正确;
⑤∠B=∠E,∠B不一定与∠F相等,结论⑤不一定正确.故选D.
15.①②
16.95 [解析]
∵△OAD≌△OBC,
∴∠OAD=∠OBC.
在△OBC中,∠O=65°,∠C=20°,
∴∠OBC=180°-(65°+20°)=95°,
∴∠OAD=∠OBC=95°.
17.解:(1)∵△ACE≌△DBF,
∴AC=DB,
∴AC-BC=DB-BC,即AB=DC.
∵AD=AB+BC+DC=30,BC=6,
∴AB=12,
∴AC=AB+BC=12+6=18.
(2)证明:∵△ACE≌△DBF,
∴∠ECA=∠FBD,∴CE∥BF.
18.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠B=∠D=25°,
∴∠BAC=(∠EAB-∠CAD)=×110°=55°,
∴∠DFB=∠DAB+∠B=∠CAD+∠BAC+∠B=10°+55°+25°=90°,
∴∠DGB=∠DFB-∠D=90°-25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
19.解:设∠3=3x,则∠1=28x,∠2=5x.
∵∠1+∠2+∠3=180°,
∴28x+5x+3x=180°,
解得x=5°,
∴∠1=140°,∠2=25°,∠3=15°.
∵△ABE是△ABC沿着AB边翻折180°形成的,
∴△ABE≌△ABC,
∴∠BAE=∠1=140°,∠E=∠3=15°,
∴∠EAC=360°-∠BAE-∠1=360°-140°-140°=80°.
∵△ADC是△ABC沿着AC边翻折180°形成的,
∴△ADC≌△ABC,
∴∠ACD=∠3=15°,
∴∠ACD=∠E.
而由三角形内角和定理及对顶角相等,得∠α+∠E=∠EAC+∠ACD,
∴∠α=∠EAC=80°.
【基础练习】
知识点
1 全等图形的概念
1.下列说法中错误的是
( )
A.能够完全重合的两个图形叫全等图形
B.面积相等的两个图形是全等图形
C.全等图形的形状和大小都一样
D.平移、轴对称、旋转前后的两个三角形是全等图形
2.下列各组的两个图形中属于全等图形的是
( )
图1
知识点
2 全等三角形及其有关概念
3.如图2所示,沿直线AC对折,△ABC与△ADC能互相重合,则△ABC≌ ,AB的对应边是 ,∠BCA的对应角是 .?
图2
4.如图3,△ABC≌△DEF,BC∥EF,AC∥DF,则∠C的对应角是
( )
图3
A.∠F
B.∠AGF
C.∠AEF
D.∠D
5.填表格:剪两个全等三角形,按下列位置摆一摆,并指出它们的对应顶点、对应角、对应边.
图形
对应顶点
对应角
对应边
知识点
3 全等三角形的性质
6.如图4,△ABC≌△CDA,AB=5,BC=7,AC=6,则AD边的长为
( )
图4
A.5
B.6
C.7
D.不确定
7.如图5,已知△ABC≌△ADC,∠B+∠D=160°,则∠B的度数是
( )
图5
A.80°
B.90°
C.100°
D.120°
8.[2020·淄博]
如图6,若△ABC≌△ADE,则下列结论中一定成立的是
( )
图6
A.AC=DE
B.∠BAD=∠CAE
C.AB=AE
D.∠ABC=∠AED
9.如图7所示,若△ABE≌△ACF,且AB=5,AE=3,则EC的长为 .?
图7
10.已知△ABC≌△DEF,∠A=70°,∠E=30°,则∠F的度数为 .?
11.已知△ABC≌△DEF,∠A=80°,∠E-∠F=20°,求△DEF各内角的度数.
12.如图8所示,已知AB与CD相交于点O,△AOC≌△BOD.求证:AC∥BD.
图8
【能力提升】
13.如图9,△ABD≌△ACE,∠AEC=110°,则∠DAE的度数为
( )
图9
A.40°
B.30°
C.50°
D.60°
14.如图10所示,点A,D,C,F在同一条直线上,且△ABC≌△FED.有下列结论:①AD=CF;
②AB∥EF;③BC∥DE且BC=DE;④∠A=∠E;⑤∠B=∠F.其中一定正确的结论是( )
图10
A.①③⑤ B.②④
C.①②
D.①②③
15.图12中,与图11中的图形全等的有 (填序号).?
图11
图12
16.如图13所示,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= °.?
图13
17.已知:如图14,△ACE≌△DBF,AD=30,BC=6.
(1)求AC的长;
(2)求证:CE∥BF.
图14
18.如图15,△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,BC的延长线与AD交于点F,与DE交于点G,求∠DFB和∠DGB的度数.
图15
19.如图16所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的.若∠1∶∠2∶∠3=28∶5∶3,求∠α的度数.
图16
答案
1.B 2.D
3.△ADC AD ∠DCA
4.A [解析]
根据全等三角形对应角的定义可知∠C与∠F是对应角.
5.解:
图形
对应顶点
对应角
对应边
点A与点D,点B与点E,点C与点F
∠A与∠D,∠B与∠DEF,∠ACB与∠F
AB与DE,BC与EF,AC与DF
点A与点D,点B与点F,点C与点E
∠A与∠D,∠ABC与∠DFE,∠ACB与∠DEF
AB与DF,BC与FE,AC与DE
点A与点D,点B与点E,点C与点F
∠A与∠D,∠B与∠E,∠ACB与∠AFE
AB与DE,BC与EF,AC与DF
6.C [解析]
∵△ABC≌△CDA,∴AD=BC=7.故选C.
7.A [解析]
∵△ABC≌△ADC,∴∠B=∠D.又∵∠B+∠D=160°,∴∠B=80°.故选A.
8.B [解析]
∵△ABC≌△ADE,
∴AC=AE,AB=AD,∠ABC=∠ADE,∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
故A,C,D选项错误,B选项正确.
故选B.
9.2 [解析]
∵△ABE≌△ACF,
∴AC=AB=5,
∴EC=AC-AE=2.
故答案为2.
10.80° [解析]
∵△ABC≌△DEF,∴∠D=∠A=70°,∴∠F=180°-∠D-∠E=180°-70°-30°=80°.
11.解:∵△ABC≌△DEF,
∴∠D=∠A=80°,∴∠E+∠F=100°.
又∵∠E-∠F=20°,
∴∠E=60°,∠F=40°.
即∠D=80°,∠E=60°,∠F=40°.
12.证明:∵△AOC≌△BOD,
∴∠A=∠B(全等三角形的对应角相等),
∴AC∥BD(内错角相等,两直线平行).
13.A [解析]
∵∠AEC=110°,∴∠AED=180°-∠AEC=180°-110°=70°.∵△ABD≌△ACE,
∴AD=AE,∴∠AED=∠ADE,∴∠DAE=180°-2×70°=180°-140°=40°.
14.D [解析]
∵△ABC≌△FED,∴①AC=FD,∴AD=AC-CD=FD-CD=CF,结论①正确;
②∠A=∠F,∴AB∥EF,结论②正确;
③∠ACB=∠FDE,∴BC∥DE,又BC=DE,∴结论③正确;
④∠A=∠F,∠A不一定与∠E相等,结论④不一定正确;
⑤∠B=∠E,∠B不一定与∠F相等,结论⑤不一定正确.故选D.
15.①②
16.95 [解析]
∵△OAD≌△OBC,
∴∠OAD=∠OBC.
在△OBC中,∠O=65°,∠C=20°,
∴∠OBC=180°-(65°+20°)=95°,
∴∠OAD=∠OBC=95°.
17.解:(1)∵△ACE≌△DBF,
∴AC=DB,
∴AC-BC=DB-BC,即AB=DC.
∵AD=AB+BC+DC=30,BC=6,
∴AB=12,
∴AC=AB+BC=12+6=18.
(2)证明:∵△ACE≌△DBF,
∴∠ECA=∠FBD,∴CE∥BF.
18.解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,∠B=∠D=25°,
∴∠BAC=(∠EAB-∠CAD)=×110°=55°,
∴∠DFB=∠DAB+∠B=∠CAD+∠BAC+∠B=10°+55°+25°=90°,
∴∠DGB=∠DFB-∠D=90°-25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
19.解:设∠3=3x,则∠1=28x,∠2=5x.
∵∠1+∠2+∠3=180°,
∴28x+5x+3x=180°,
解得x=5°,
∴∠1=140°,∠2=25°,∠3=15°.
∵△ABE是△ABC沿着AB边翻折180°形成的,
∴△ABE≌△ABC,
∴∠BAE=∠1=140°,∠E=∠3=15°,
∴∠EAC=360°-∠BAE-∠1=360°-140°-140°=80°.
∵△ADC是△ABC沿着AC边翻折180°形成的,
∴△ADC≌△ABC,
∴∠ACD=∠3=15°,
∴∠ACD=∠E.
而由三角形内角和定理及对顶角相等,得∠α+∠E=∠EAC+∠ACD,
∴∠α=∠EAC=80°.
同课章节目录
