2021——2022学年湘教版九年级数学上册3.4.1 相似三角形的判定定理2 练习题 (word版含答案)
文档属性
| 名称 | 2021——2022学年湘教版九年级数学上册3.4.1 相似三角形的判定定理2 练习题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 09:38:26 | ||
图片预览


文档简介
第3课时 相似三角形的判定定理2
【基础练习】
知识点 两边成比例且夹角相等的两个三角形相似
1.已知△ABC如图2所示,则图3中与△ABC相似的是
( )
图2
图3
2.如图4,△ACD和△ABC相似需具备的条件是
( )
图4
A.=
B.=
C.AC2=AD·AB
D.CD2=AD·BD
3.如图5,四边形ABCD的对角线AC,BD相交于点O,且将这个四边形分成①②③④四个三角形.若OA∶OC=OB∶OD,则下列结论中一定正确的是
( )
图5
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
4.如图6,已知∠1=∠2,那么添加下列哪一个条件后,仍无法判定△ABC∽△ADE
( )
图6
A.∠C=∠E
B.∠B=∠ADE
C.=
D.=
5.如图7,DE与BC不平行,当= 时,△AED∽△ABC.?
图7
6.如图8,在△ABC中,P是AC边上一点,连接BP.
图8
(1)当∠APB= 时,△APB∽△ABC;?
(2)当AB∶AP= 时,△APB∽△ABC.?
7.如图9,AB·AD=AC·AE.
求证:△ABC∽△AED.
图9
8.如图10,在△ABC中,CD⊥AB于点D,AC2=AD·AB.求证:△ABC是直角三角形.
图10
【能力提升】
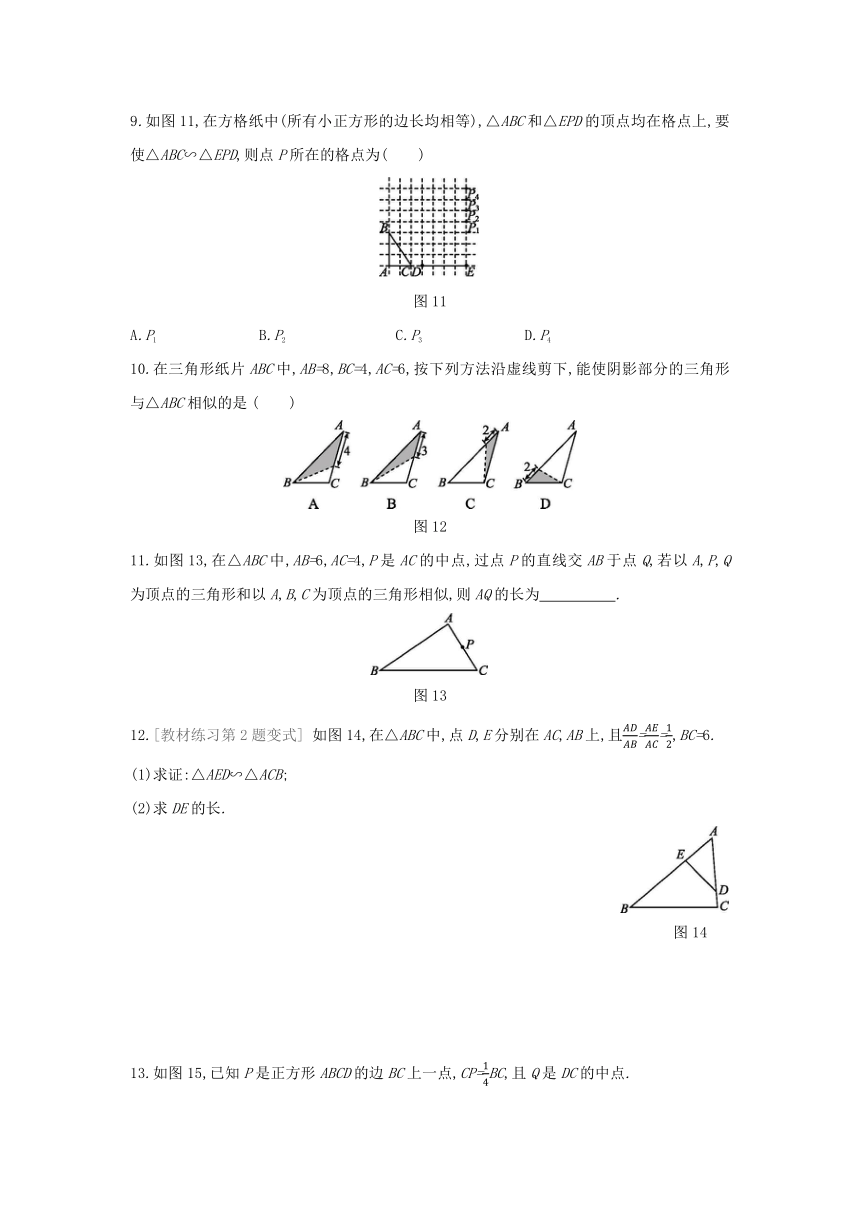
9.如图11,在方格纸中(所有小正方形的边长均相等),△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
图11
A.P1
B.P2
C.P3
D.P4
10.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是
( )
图12
11.如图13,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和以A,B,C为顶点的三角形相似,则AQ的长为 .?
图13
12.[教材练习第2题变式]
如图14,在△ABC中,点D,E分别在AC,AB上,且==,BC=6.
(1)求证:△AED∽△ACB;
(2)求DE的长.
图14
13.如图15,已知P是正方形ABCD的边BC上一点,CP=BC,且Q是DC的中点.
求证:△ADQ∽△QCP.
图15
14.如图16,已知AB⊥DB于点B,CD⊥DB于点D,AB=6,CD=4,BD=14,在DB上取一点P,使以C,D,P为顶点的三角形与以P,B,A为顶点的三角形相似,求DP的长.
图16
15.如图17,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线BA,垂足为A,作y轴的垂线BC,垂足为C.点D从点O出发,沿y轴正方向以每秒1个单位的速度运动;点E从点O出发,沿x轴正方向以每秒3个单位的速度运动;点F从点B出发,沿BA方向以每秒2个单位的速度运动.当点E运动到点A时,三点都停止运动.设运动时间为t秒.
(1)用含t的式子分别表示点E,F的坐标;
(2)若△ODE与以A,E,F为顶点的三角形相似,求t的值.
图17
答案
1.C
2.C [解析]
题目中隐含条件∠A=∠A,根据“两边成比例且夹角相等的两个三角形相似”,得出添加的条件可以是=,即AC2=AD·AB.故选C.
3.B
4.D [解析]
由∠1=∠2可知,∠BAC=∠DAE,利用两角分别对应相等或两边对应成比例且夹角相等可以判定两三角形相似,因此添加条件后仍无法判定△ABC∽△ADE的是D选项.
5.
6.(1)∠ABC (2)AC∶AB
7.证明:∵AB·AD=AC·AE,
∴=.
又∵∠BAC=∠EAD,
∴△ABC∽△AED.
8.证明:∵AC2=AD·AB,∴=.
又∵∠A为公共角,
∴△ABC∽△ACD,
∴∠ACB=∠ADC=90°,
∴△ABC是直角三角形.
9.C
10.D [解析]
观察图形可以知道阴影部分的三角形与△ABC都有一个公共角,故要判断这两个三角形是否相似,只需看夹公共角的两边是否成比例即可.逐一排除后发现只有选项D符合要求.故选D.
11.3或 [解析]∵AC=4,P是AC的中点,∴AP=AC=2.①若△APQ∽△ACB,则=,即=,解得AQ=3;②若△APQ∽△ABC,则=,即=,解得AQ=.
∴AQ的长为3或.
12.解:(1)证明:∵=,且∠A=∠A,
∴△AED∽△ACB.
(2)∵△AED∽△ACB,
∴==.
∵BC=6,∴DE=3.
13.证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠C=∠D=90°.
∵CP=BC,CQ=DQ=DC,
∴==,
∴△ADQ∽△QCP.
14.解:∵AB⊥DB,CD⊥DB,
∴∠D=∠B=90°.
设DP=x,则BP=14-x.
若△PDC∽△ABP,则DP∶BA=CD∶PB,
∴=,解得x=2或x=12.
经检验,均符合题意.
若△PCD∽△PAB,则DP∶BP=CD∶AB,
∴=,解得x=5.6.
经检验,符合题意.
故DP的长为5.6或2或12.
15.解:(1)由题意得OE=3t,OD=t,BF=2t.
∵BA⊥x轴,BC⊥y轴,∠AOC=90°,
∴∠AOC=∠BAO=∠BCO=90°,
∴四边形OABC是矩形,
∴AB=OC,BC=OA.
∵B(12,10),∴BC=OA=12,AB=OC=10,
∴AF=10-2t,AE=12-3t,
∴点E的坐标为(3t,0),点F的坐标为(12,10-2t).
(2)①当△ODE∽△AEF时,有=,
∴=,
解得t1=0(不符合题意,舍去),t2=;
②当△ODE∽△AFE时,有=,
∴=,
解得t1=0(不符合题意,舍去),t2=6.
∵点E运动到点A时,三点都停止运动,
∴3t≤12,∴t≤4.
∵6>4,∴t=6舍去,∴t=.
综上所述,t的值为.
【基础练习】
知识点 两边成比例且夹角相等的两个三角形相似
1.已知△ABC如图2所示,则图3中与△ABC相似的是
( )
图2
图3
2.如图4,△ACD和△ABC相似需具备的条件是
( )
图4
A.=
B.=
C.AC2=AD·AB
D.CD2=AD·BD
3.如图5,四边形ABCD的对角线AC,BD相交于点O,且将这个四边形分成①②③④四个三角形.若OA∶OC=OB∶OD,则下列结论中一定正确的是
( )
图5
A.①和②相似
B.①和③相似
C.①和④相似
D.②和④相似
4.如图6,已知∠1=∠2,那么添加下列哪一个条件后,仍无法判定△ABC∽△ADE
( )
图6
A.∠C=∠E
B.∠B=∠ADE
C.=
D.=
5.如图7,DE与BC不平行,当= 时,△AED∽△ABC.?
图7
6.如图8,在△ABC中,P是AC边上一点,连接BP.
图8
(1)当∠APB= 时,△APB∽△ABC;?
(2)当AB∶AP= 时,△APB∽△ABC.?
7.如图9,AB·AD=AC·AE.
求证:△ABC∽△AED.
图9
8.如图10,在△ABC中,CD⊥AB于点D,AC2=AD·AB.求证:△ABC是直角三角形.
图10
【能力提升】
9.如图11,在方格纸中(所有小正方形的边长均相等),△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
图11
A.P1
B.P2
C.P3
D.P4
10.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是
( )
图12
11.如图13,在△ABC中,AB=6,AC=4,P是AC的中点,过点P的直线交AB于点Q,若以A,P,Q为顶点的三角形和以A,B,C为顶点的三角形相似,则AQ的长为 .?
图13
12.[教材练习第2题变式]
如图14,在△ABC中,点D,E分别在AC,AB上,且==,BC=6.
(1)求证:△AED∽△ACB;
(2)求DE的长.
图14
13.如图15,已知P是正方形ABCD的边BC上一点,CP=BC,且Q是DC的中点.
求证:△ADQ∽△QCP.
图15
14.如图16,已知AB⊥DB于点B,CD⊥DB于点D,AB=6,CD=4,BD=14,在DB上取一点P,使以C,D,P为顶点的三角形与以P,B,A为顶点的三角形相似,求DP的长.
图16
15.如图17,在平面直角坐标系中,点B(12,10),过点B作x轴的垂线BA,垂足为A,作y轴的垂线BC,垂足为C.点D从点O出发,沿y轴正方向以每秒1个单位的速度运动;点E从点O出发,沿x轴正方向以每秒3个单位的速度运动;点F从点B出发,沿BA方向以每秒2个单位的速度运动.当点E运动到点A时,三点都停止运动.设运动时间为t秒.
(1)用含t的式子分别表示点E,F的坐标;
(2)若△ODE与以A,E,F为顶点的三角形相似,求t的值.
图17
答案
1.C
2.C [解析]
题目中隐含条件∠A=∠A,根据“两边成比例且夹角相等的两个三角形相似”,得出添加的条件可以是=,即AC2=AD·AB.故选C.
3.B
4.D [解析]
由∠1=∠2可知,∠BAC=∠DAE,利用两角分别对应相等或两边对应成比例且夹角相等可以判定两三角形相似,因此添加条件后仍无法判定△ABC∽△ADE的是D选项.
5.
6.(1)∠ABC (2)AC∶AB
7.证明:∵AB·AD=AC·AE,
∴=.
又∵∠BAC=∠EAD,
∴△ABC∽△AED.
8.证明:∵AC2=AD·AB,∴=.
又∵∠A为公共角,
∴△ABC∽△ACD,
∴∠ACB=∠ADC=90°,
∴△ABC是直角三角形.
9.C
10.D [解析]
观察图形可以知道阴影部分的三角形与△ABC都有一个公共角,故要判断这两个三角形是否相似,只需看夹公共角的两边是否成比例即可.逐一排除后发现只有选项D符合要求.故选D.
11.3或 [解析]∵AC=4,P是AC的中点,∴AP=AC=2.①若△APQ∽△ACB,则=,即=,解得AQ=3;②若△APQ∽△ABC,则=,即=,解得AQ=.
∴AQ的长为3或.
12.解:(1)证明:∵=,且∠A=∠A,
∴△AED∽△ACB.
(2)∵△AED∽△ACB,
∴==.
∵BC=6,∴DE=3.
13.证明:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠C=∠D=90°.
∵CP=BC,CQ=DQ=DC,
∴==,
∴△ADQ∽△QCP.
14.解:∵AB⊥DB,CD⊥DB,
∴∠D=∠B=90°.
设DP=x,则BP=14-x.
若△PDC∽△ABP,则DP∶BA=CD∶PB,
∴=,解得x=2或x=12.
经检验,均符合题意.
若△PCD∽△PAB,则DP∶BP=CD∶AB,
∴=,解得x=5.6.
经检验,符合题意.
故DP的长为5.6或2或12.
15.解:(1)由题意得OE=3t,OD=t,BF=2t.
∵BA⊥x轴,BC⊥y轴,∠AOC=90°,
∴∠AOC=∠BAO=∠BCO=90°,
∴四边形OABC是矩形,
∴AB=OC,BC=OA.
∵B(12,10),∴BC=OA=12,AB=OC=10,
∴AF=10-2t,AE=12-3t,
∴点E的坐标为(3t,0),点F的坐标为(12,10-2t).
(2)①当△ODE∽△AEF时,有=,
∴=,
解得t1=0(不符合题意,舍去),t2=;
②当△ODE∽△AFE时,有=,
∴=,
解得t1=0(不符合题意,舍去),t2=6.
∵点E运动到点A时,三点都停止运动,
∴3t≤12,∴t≤4.
∵6>4,∴t=6舍去,∴t=.
综上所述,t的值为.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
