2021—2022学年湘教版九年级数学上册3.6位似练习题 (共2课时、word版、含解析)
文档属性
| 名称 | 2021—2022学年湘教版九年级数学上册3.6位似练习题 (共2课时、word版、含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 380.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 00:00:00 | ||
图片预览


文档简介
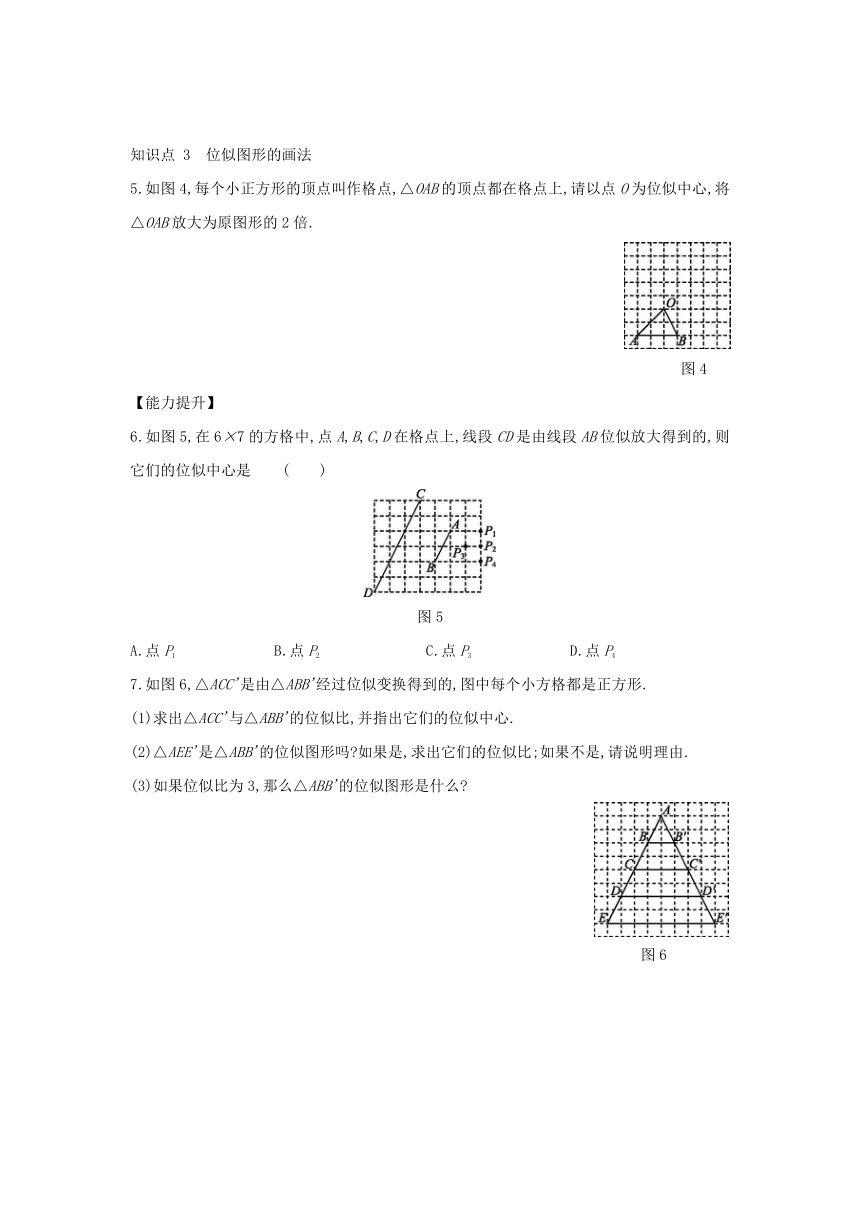
3.6 位似
位似图形的概念及画法
【基础练习】
知识点
1 位似图形的概念和识别
1.下列图形中不是位似图形的是
( )
图1
2.下列判断中正确的是
( )
A.相似图形一定是位似图形
B.位似图形一定是相似图形
C.全等图形一定是位似图形
D.位似图形一定是全等图形
知识点
2 位似图形的性质
3.[2019·邵阳]
如图2,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法中错误的是
( )
A.△ABC∽△A'B'C'
B.C,O,C'三点在同一直线上
C.AO∶AA'=1∶2
D.AB∥A'B'
图2
图3
4.[2020·重庆]
如图3,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为
( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
知识点
3 位似图形的画法
5.如图4,每个小正方形的顶点叫作格点,△OAB的顶点都在格点上,请以点O为位似中心,将△OAB放大为原图形的2倍.
图4
【能力提升】
6.如图5,在6×7的方格中,点A,B,C,D在格点上,线段CD是由线段AB位似放大得到的,则它们的位似中心是
( )
图5
A.点P1
B.点P2
C.点P3
D.点P4
7.如图6,△ACC'是由△ABB'经过位似变换得到的,图中每个小方格都是正方形.
(1)求出△ACC'与△ABB'的位似比,并指出它们的位似中心.
(2)△AEE'是△ABB'的位似图形吗?如果是,求出它们的位似比;如果不是,请说明理由.
(3)如果位似比为3,那么△ABB'的位似图形是什么?
图6
8.如图7,在18×13的网格中,每个小正方形的边长都是1.△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)在图中画出位似中心O(要保留画图痕迹);
(2)△ABC与△A'B'C'的位似比是 .?
图7
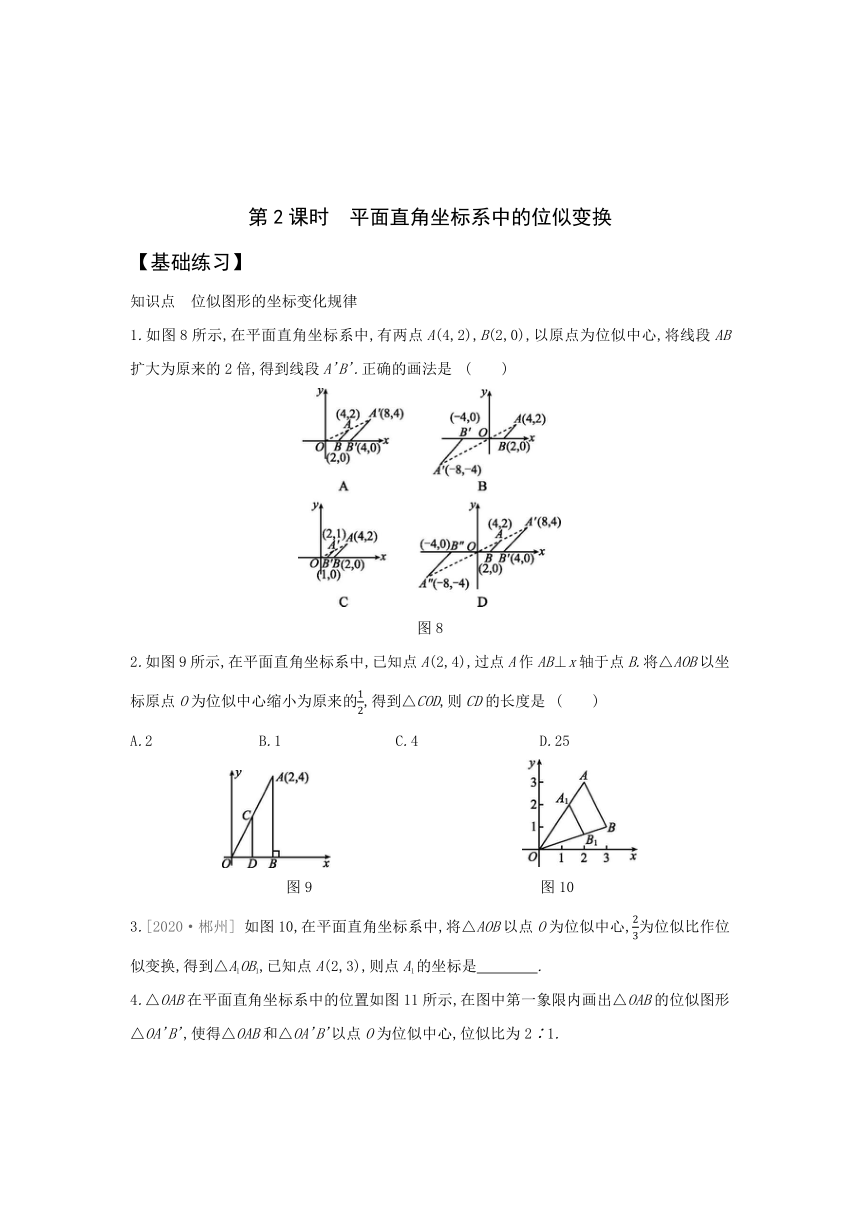
平面直角坐标系中的位似变换
【基础练习】
知识点 位似图形的坐标变化规律
1.如图8所示,在平面直角坐标系中,有两点A(4,2),B(2,0),以原点为位似中心,将线段AB扩大为原来的2倍,得到线段A'B'.正确的画法是
( )
图8
2.如图9所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原来的,得到△COD,则CD的长度是
( )
A.2
B.1
C.4
D.25
图9
图10
3.[2020·郴州]
如图10,在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知点A(2,3),则点A1的坐标是 .?
4.△OAB在平面直角坐标系中的位置如图11所示,在图中第一象限内画出△OAB的位似图形△OA'B',使得△OAB和△OA'B'以点O为位似中心,位似比为2∶1.
图11
【能力提升】
5.如图12,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .?
图12
6.如图13,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标为(-1,0),以点C为位似中心,并将△ABC的边长放大到原来的2倍,在x轴的下方作△ABC的位似图形△A'B'C.设点B的横坐标是a,则点B'的横坐标是 .?
图13
7.如图14,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出点C1的坐标;
(2)以原点O为位似中心,位似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变换后点D的对应点D2的坐标.
图14
答案
第1课时
1.D
2.B [解析]
如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形,故选项A错误,选项B正确;全等图形不一定是位似图形,故选项C错误;位似图形是特殊的相似图形,相似图形不一定是全等图形,故选项D错误.
3.C [解析]∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',
∴△ABC∽△A'B'C',C,O,C'三点在同一直线上,AB∥A'B',AO∶OA'=1∶2,故选项C错误,符合题意.故选C.
4.C [解析]∵△ABC与△DEF是位似图形,OA∶OD=1∶2,
∴△ABC与△DEF的位似比是1∶2,
∴△ABC与△DEF的相似比为1∶2,
∴△ABC与△DEF的面积比为1∶4.故选C.
5.解:如图:
6.C [解析]
连接CA,DB并延长,交点即为它们的位似中心,继而可求得答案.
7.解:(1)△ACC'与△ABB'的位似比为CC'∶BB'=2∶1,它们的位似中心是点A.
(2)△AEE'是△ABB'的位似图形,位似比为EE'∶BB'=4∶1.
(3)如果位似比为3,那么△ABB'的位似图形是△ADD'.
8.解:(1)如图所示:
(2)∵B'C'=2,BC=,
∴==,
∴△ABC与△A'B'C'的位似比是1∶2
第2课时
1.D [解析]
根据题意分两种情况画出满足题意的线段A'B',即可做出判断.
2.A
3.,2 [解析]∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是×2,×3,即A1,2.
4.略
5.4.5 [解析]∵△ABC与△DEF是位似图形,它们的位似中心为原点,已知点A的坐标为(1,0),点D的坐标为(3,0),∴AO=1,DO=3,
∴==.∵AB=1.5,∴DE=4.5.
6.-2a-3 [解析]
如图,分别过点B和点B'作x轴的垂线,垂足分别是D和E.∵点B的横坐标是a,点C的坐标是(-1,0),△A'B'C是△ABC的边长放大2倍得到的,∴EC=2(-a-1),∴点B'的横坐标是2(-a-1)-1=-2a-3.
7.解:(1)如图所示.∵点C的坐标为(-3,2),点C和点C1关于y轴对称,∴点C1的坐标为(3,2).
(2)如图所示,连接OA并延长至点A2,使A2A=OA,连接OB并延长至点B2,使B2B=OB,连接OC并延长至点C2,使C2C=OC,连接A2B2,A2C2,B2C2,可得出△A2B2C2为所求作的三角形.
∵点C的坐标为(-3,2),△ABC∽△A2B2C2,位似比为1∶2,
∴点C2的坐标为(-6,4).
(3)由点A2,B2,C2的坐标与点A,B,C的坐标的关系,可以探求点D,D2的坐标的关系.
∵点D的坐标为(a,b),∴点D2的坐标为(2a,2b).
位似图形的概念及画法
【基础练习】
知识点
1 位似图形的概念和识别
1.下列图形中不是位似图形的是
( )
图1
2.下列判断中正确的是
( )
A.相似图形一定是位似图形
B.位似图形一定是相似图形
C.全等图形一定是位似图形
D.位似图形一定是全等图形
知识点
2 位似图形的性质
3.[2019·邵阳]
如图2,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',以下说法中错误的是
( )
A.△ABC∽△A'B'C'
B.C,O,C'三点在同一直线上
C.AO∶AA'=1∶2
D.AB∥A'B'
图2
图3
4.[2020·重庆]
如图3,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为
( )
A.1∶2
B.1∶3
C.1∶4
D.1∶5
知识点
3 位似图形的画法
5.如图4,每个小正方形的顶点叫作格点,△OAB的顶点都在格点上,请以点O为位似中心,将△OAB放大为原图形的2倍.
图4
【能力提升】
6.如图5,在6×7的方格中,点A,B,C,D在格点上,线段CD是由线段AB位似放大得到的,则它们的位似中心是
( )
图5
A.点P1
B.点P2
C.点P3
D.点P4
7.如图6,△ACC'是由△ABB'经过位似变换得到的,图中每个小方格都是正方形.
(1)求出△ACC'与△ABB'的位似比,并指出它们的位似中心.
(2)△AEE'是△ABB'的位似图形吗?如果是,求出它们的位似比;如果不是,请说明理由.
(3)如果位似比为3,那么△ABB'的位似图形是什么?
图6
8.如图7,在18×13的网格中,每个小正方形的边长都是1.△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
(1)在图中画出位似中心O(要保留画图痕迹);
(2)△ABC与△A'B'C'的位似比是 .?
图7
平面直角坐标系中的位似变换
【基础练习】
知识点 位似图形的坐标变化规律
1.如图8所示,在平面直角坐标系中,有两点A(4,2),B(2,0),以原点为位似中心,将线段AB扩大为原来的2倍,得到线段A'B'.正确的画法是
( )
图8
2.如图9所示,在平面直角坐标系中,已知点A(2,4),过点A作AB⊥x轴于点B.将△AOB以坐标原点O为位似中心缩小为原来的,得到△COD,则CD的长度是
( )
A.2
B.1
C.4
D.25
图9
图10
3.[2020·郴州]
如图10,在平面直角坐标系中,将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,已知点A(2,3),则点A1的坐标是 .?
4.△OAB在平面直角坐标系中的位置如图11所示,在图中第一象限内画出△OAB的位似图形△OA'B',使得△OAB和△OA'B'以点O为位似中心,位似比为2∶1.
图11
【能力提升】
5.如图12,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE= .?
图12
6.如图13,在△ABC中,A,B两个顶点在x轴的上方,点C的坐标为(-1,0),以点C为位似中心,并将△ABC的边长放大到原来的2倍,在x轴的下方作△ABC的位似图形△A'B'C.设点B的横坐标是a,则点B'的横坐标是 .?
图13
7.如图14,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-2,1),B(-1,4),C(-3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出点C1的坐标;
(2)以原点O为位似中心,位似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出点C2的坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变换后点D的对应点D2的坐标.
图14
答案
第1课时
1.D
2.B [解析]
如果两个图形是位似图形,那么这两个图形必是相似图形,但是相似的两个图形不一定是位似图形,故选项A错误,选项B正确;全等图形不一定是位似图形,故选项C错误;位似图形是特殊的相似图形,相似图形不一定是全等图形,故选项D错误.
3.C [解析]∵以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C',
∴△ABC∽△A'B'C',C,O,C'三点在同一直线上,AB∥A'B',AO∶OA'=1∶2,故选项C错误,符合题意.故选C.
4.C [解析]∵△ABC与△DEF是位似图形,OA∶OD=1∶2,
∴△ABC与△DEF的位似比是1∶2,
∴△ABC与△DEF的相似比为1∶2,
∴△ABC与△DEF的面积比为1∶4.故选C.
5.解:如图:
6.C [解析]
连接CA,DB并延长,交点即为它们的位似中心,继而可求得答案.
7.解:(1)△ACC'与△ABB'的位似比为CC'∶BB'=2∶1,它们的位似中心是点A.
(2)△AEE'是△ABB'的位似图形,位似比为EE'∶BB'=4∶1.
(3)如果位似比为3,那么△ABB'的位似图形是△ADD'.
8.解:(1)如图所示:
(2)∵B'C'=2,BC=,
∴==,
∴△ABC与△A'B'C'的位似比是1∶2
第2课时
1.D [解析]
根据题意分两种情况画出满足题意的线段A'B',即可做出判断.
2.A
3.,2 [解析]∵将△AOB以点O为位似中心,为位似比作位似变换,得到△A1OB1,A(2,3),∴点A1的坐标是×2,×3,即A1,2.
4.略
5.4.5 [解析]∵△ABC与△DEF是位似图形,它们的位似中心为原点,已知点A的坐标为(1,0),点D的坐标为(3,0),∴AO=1,DO=3,
∴==.∵AB=1.5,∴DE=4.5.
6.-2a-3 [解析]
如图,分别过点B和点B'作x轴的垂线,垂足分别是D和E.∵点B的横坐标是a,点C的坐标是(-1,0),△A'B'C是△ABC的边长放大2倍得到的,∴EC=2(-a-1),∴点B'的横坐标是2(-a-1)-1=-2a-3.
7.解:(1)如图所示.∵点C的坐标为(-3,2),点C和点C1关于y轴对称,∴点C1的坐标为(3,2).
(2)如图所示,连接OA并延长至点A2,使A2A=OA,连接OB并延长至点B2,使B2B=OB,连接OC并延长至点C2,使C2C=OC,连接A2B2,A2C2,B2C2,可得出△A2B2C2为所求作的三角形.
∵点C的坐标为(-3,2),△ABC∽△A2B2C2,位似比为1∶2,
∴点C2的坐标为(-6,4).
(3)由点A2,B2,C2的坐标与点A,B,C的坐标的关系,可以探求点D,D2的坐标的关系.
∵点D的坐标为(a,b),∴点D2的坐标为(2a,2b).
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
