2021-2022学年湘教版八年级数学上册第2章 三角形 单元复习训练(word解析版)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学上册第2章 三角形 单元复习训练(word解析版) |  | |
| 格式 | docx | ||
| 文件大小 | 147.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 11:25:36 | ||
图片预览



文档简介
第2章 三角形
类型之一 三角形的边和角
1.[2020·济宁]
已知三角形的两边长分别为3和6,则这个三角形的第三边长可以是 (写出一个即可).?
2.[2019·大庆]
如图1,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E.若∠A=60°,则∠BEC的度数是
( )
图1
A.15°
B.30°
C.45°
D.60°
3.如图2所示,已知AD是△ABC的高,AE是△ABC的角平分线,∠B=26°,∠ACD=56°,求
∠AED的度数.
图2
类型之二 命题与证明
4.有下列两个命题:①若两个角是对顶角,则这两个角相等;②若一个三角形的两个内角分别为30°和60°,则这个三角形是直角三角形.下列说法中正确的是
( )
A.命题①正确,命题②不正确
B.命题①②都正确
C.命题①不正确,命题②正确
D.命题①②都不正确
5.[2019·安徽]
命题“如果a+b=0,那么a,b互为相反数”的逆命题为
.?
6.把下列命题改写成“如果……,那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)相等的角是对顶角.
类型之三 等腰三角形
7.如图3,在△ABC中,∠C=29°,D为边AC上一点,且AB=AD,DB=DC,则∠A的度数为( )
图3
A.54°
B.58°
C.61°
D.64°
8.[2020·宜昌]
如图4,在一个池塘两旁分别有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.?
图4
9.如图5,点G在BC的延长线上,∠ABC的平分线BF与∠ACG的平分线CF相交于点F,过点F作DF∥BC交AC于点E,交AB于点D.若BD=8,DE=3,求CE的长.
图5
类型之四 线段的垂直平分线
10.如图6,在△ABC中,∠B=35°,∠BAC的平分线AD交BC于点D.若DE垂直平分AB,则∠C的度数为
( )
图6
A.80°
B.75°
C.65°
D.60°
11.如图7,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,AE=5
cm,△ABD的周长为17
cm,求△ABC的周长.
图7
类型之五 全等三角形
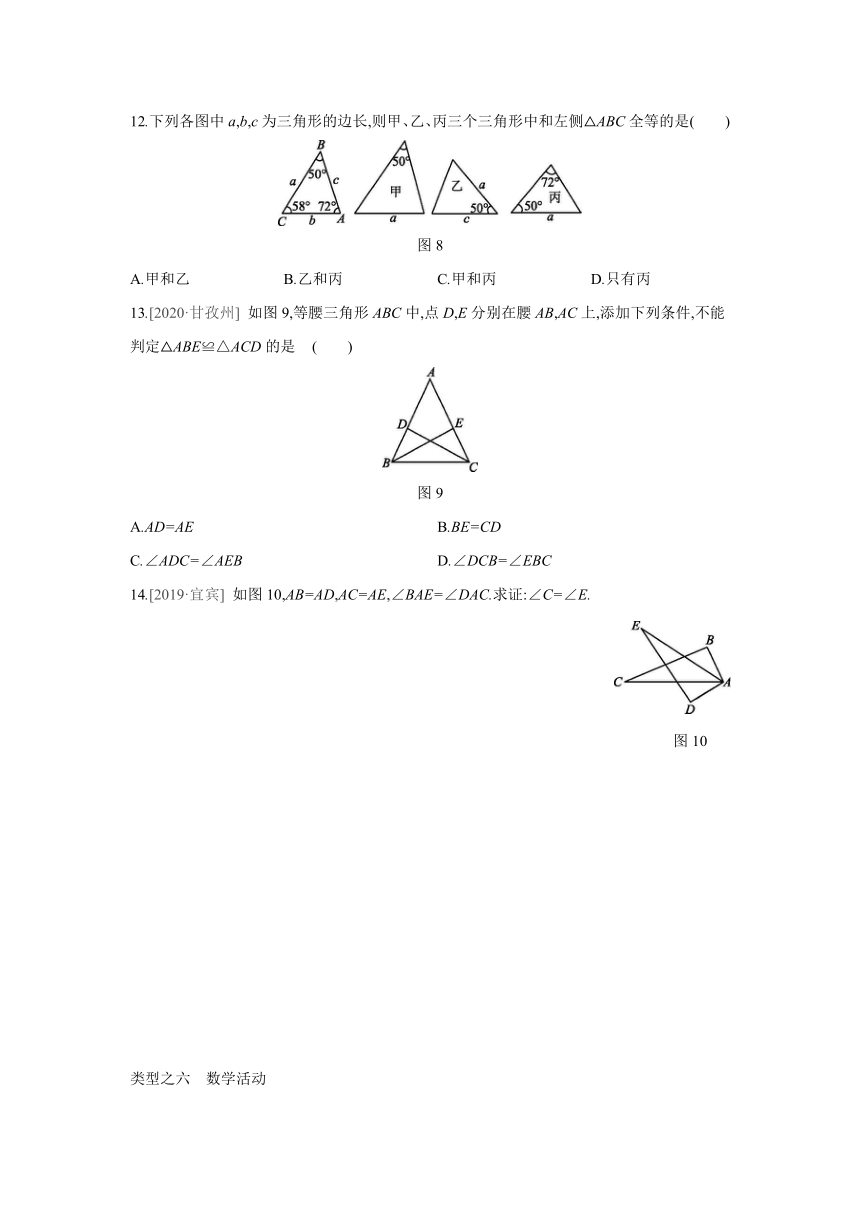
12.下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形中和左侧△ABC全等的是( )
图8
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
13.[2020·甘孜州]
如图9,等腰三角形ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是
( )
图9
A.AD=AE
B.BE=CD
C.∠ADC=∠AEB
D.∠DCB=∠EBC
14.[2019·宜宾]
如图10,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
图10
类型之六 数学活动
15.自主学习,学以致用
先阅读,再回答问题:如图11①,在△ABC中,AD为中线.延长AD至点E,使DE=AD.在△ABD和△ECD中,AD=ED,∠ADB=∠EDC,BD=CD,所以△ABD≌△ECD(SAS),进一步可得到AB=CE,AB∥CE等结论.
在已知三角形的中线时,我们经常用“倍长中线”的方法来构造全等三角形,并进一步解决一些相关的计算或证明题.
解决问题:如图②,在△ABC中,AD是中线,F为AD上一点,且BF=AC,延长BF交AC于点E.求证:AE=EF.
图11
答案
1.5(答案不唯一)
[解析]
设第三边长为x.
根据三角形的三边关系,得6-32.B [解析]
∵BE是∠ABC的平分线,∴∠EBM=∠ABC.∵CE是外角∠ACM的平分线,
∴∠ECM=∠ACM,则∠BEC=∠ECM-∠EBM=(∠ACM-∠ABC)=∠A=30°.
3.解:∵∠B=26°,∠ACD=56°,
∴∠BAC=30°.
∵AE平分∠BAC,∴∠BAE=15°,
∴∠AED=∠B+∠BAE=26°+15°=41°.
4.B [解析]
根据对顶角相等可判断①正确;利用三角形的内角和可得到三角形的第三个角为90°,那么这个三角形是直角三角形,故②正确.故选B.
5.如果a,b互为相反数,那么a+b=0
6.解:(1)如果两个角是等角的补角,那么这两个角相等.真命题.
(2)如果两个角相等,那么这两个角是对顶角.假命题.
7.D [解析]
∵DB=DC,∠C=29°,∴∠DBC=∠C=29°,∴∠ADB=∠C+∠DBC=58°.∵AB=AD,∴∠ABD=∠ADB=58°,∴∠A=180°-∠ABD-∠ADB=64°.
8.48 [解析]
∵∠ABC=60°,∠ACB=60°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AC=BC.
∵BC=48米,
∴AC=48米.
故答案为48.
9.解:∵BF,CF分别平分∠ABC,∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG.
∵DF∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD=8,EF=CE.
∵EF=FD-DE=8-3=5,
∴CE=5.
10.B [解析]
∵DE垂直平分AB,∴DA=DB,∴∠DAB=∠B=35°.∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=35°,∴∠C=180°-35°-35°-35°=75°.
11.解:∵DE垂直平分AC,AE=5
cm,
∴DA=DC,AC=2AE=10
cm.
∵△ABD的周长为17
cm,
∴AB+BD+DA=AB+BD+DC=AB+BC=17
cm,
∴△ABC的周长为AB+BC+AC=27
cm.
12.B
13.B [解析]
∵△ABC为等腰三角形,AB,AC为腰,
∴AB=AC,∠ABC=∠ACB,
∴当AD=AE时,根据“SAS”可判定△ABE≌△ACD;
当∠AEB=∠ADC时,根据“AAS”可判定△ABE≌△ACD;
当∠DCB=∠EBC时,∠ABE=∠ACD,根据“ASA”可判定△ABE≌△ACD.
故选B.
14.证明:∵∠BAE=∠DAC,
∴∠BAE+∠CAE=∠DAC+∠CAE,
即∠CAB=∠EAD.
又∵AB=AD,AC=AE,
∴△ABC≌△ADE(SAS),
∴∠C=∠E.
15.证明:延长AD到点G,使DF=DG,连接CG,如图.
∵AD是△ABC的中线,
∴BD=CD.
在△BDF和△CDG中,
∴△BDF≌△CDG(SAS),
∴BF=CG,∠BFD=∠G.
又∵∠AFE=∠BFD,
∴∠AFE=∠G.
∵BF=CG,BF=AC,
∴CG=AC,∴∠G=∠CAF,
∴∠AFE=∠CAF,
∴AE=EF.
类型之一 三角形的边和角
1.[2020·济宁]
已知三角形的两边长分别为3和6,则这个三角形的第三边长可以是 (写出一个即可).?
2.[2019·大庆]
如图1,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE相交于点E.若∠A=60°,则∠BEC的度数是
( )
图1
A.15°
B.30°
C.45°
D.60°
3.如图2所示,已知AD是△ABC的高,AE是△ABC的角平分线,∠B=26°,∠ACD=56°,求
∠AED的度数.
图2
类型之二 命题与证明
4.有下列两个命题:①若两个角是对顶角,则这两个角相等;②若一个三角形的两个内角分别为30°和60°,则这个三角形是直角三角形.下列说法中正确的是
( )
A.命题①正确,命题②不正确
B.命题①②都正确
C.命题①不正确,命题②正确
D.命题①②都不正确
5.[2019·安徽]
命题“如果a+b=0,那么a,b互为相反数”的逆命题为
.?
6.把下列命题改写成“如果……,那么……”的形式,并判断其真假.
(1)等角的补角相等;
(2)相等的角是对顶角.
类型之三 等腰三角形
7.如图3,在△ABC中,∠C=29°,D为边AC上一点,且AB=AD,DB=DC,则∠A的度数为( )
图3
A.54°
B.58°
C.61°
D.64°
8.[2020·宜昌]
如图4,在一个池塘两旁分别有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为:∠ABC=60°,∠ACB=60°,BC=48米,则AC= 米.?
图4
9.如图5,点G在BC的延长线上,∠ABC的平分线BF与∠ACG的平分线CF相交于点F,过点F作DF∥BC交AC于点E,交AB于点D.若BD=8,DE=3,求CE的长.
图5
类型之四 线段的垂直平分线
10.如图6,在△ABC中,∠B=35°,∠BAC的平分线AD交BC于点D.若DE垂直平分AB,则∠C的度数为
( )
图6
A.80°
B.75°
C.65°
D.60°
11.如图7,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,AE=5
cm,△ABD的周长为17
cm,求△ABC的周长.
图7
类型之五 全等三角形
12.下列各图中a,b,c为三角形的边长,则甲、乙、丙三个三角形中和左侧△ABC全等的是( )
图8
A.甲和乙
B.乙和丙
C.甲和丙
D.只有丙
13.[2020·甘孜州]
如图9,等腰三角形ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是
( )
图9
A.AD=AE
B.BE=CD
C.∠ADC=∠AEB
D.∠DCB=∠EBC
14.[2019·宜宾]
如图10,AB=AD,AC=AE,∠BAE=∠DAC.求证:∠C=∠E.
图10
类型之六 数学活动
15.自主学习,学以致用
先阅读,再回答问题:如图11①,在△ABC中,AD为中线.延长AD至点E,使DE=AD.在△ABD和△ECD中,AD=ED,∠ADB=∠EDC,BD=CD,所以△ABD≌△ECD(SAS),进一步可得到AB=CE,AB∥CE等结论.
在已知三角形的中线时,我们经常用“倍长中线”的方法来构造全等三角形,并进一步解决一些相关的计算或证明题.
解决问题:如图②,在△ABC中,AD是中线,F为AD上一点,且BF=AC,延长BF交AC于点E.求证:AE=EF.
图11
答案
1.5(答案不唯一)
[解析]
设第三边长为x.
根据三角形的三边关系,得6-3
∵BE是∠ABC的平分线,∴∠EBM=∠ABC.∵CE是外角∠ACM的平分线,
∴∠ECM=∠ACM,则∠BEC=∠ECM-∠EBM=(∠ACM-∠ABC)=∠A=30°.
3.解:∵∠B=26°,∠ACD=56°,
∴∠BAC=30°.
∵AE平分∠BAC,∴∠BAE=15°,
∴∠AED=∠B+∠BAE=26°+15°=41°.
4.B [解析]
根据对顶角相等可判断①正确;利用三角形的内角和可得到三角形的第三个角为90°,那么这个三角形是直角三角形,故②正确.故选B.
5.如果a,b互为相反数,那么a+b=0
6.解:(1)如果两个角是等角的补角,那么这两个角相等.真命题.
(2)如果两个角相等,那么这两个角是对顶角.假命题.
7.D [解析]
∵DB=DC,∠C=29°,∴∠DBC=∠C=29°,∴∠ADB=∠C+∠DBC=58°.∵AB=AD,∴∠ABD=∠ADB=58°,∴∠A=180°-∠ABD-∠ADB=64°.
8.48 [解析]
∵∠ABC=60°,∠ACB=60°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AC=BC.
∵BC=48米,
∴AC=48米.
故答案为48.
9.解:∵BF,CF分别平分∠ABC,∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG.
∵DF∥BC,
∴∠DFB=∠CBF,∠EFC=∠FCG,
∴∠DBF=∠DFB,∠FCE=∠EFC,
∴BD=FD=8,EF=CE.
∵EF=FD-DE=8-3=5,
∴CE=5.
10.B [解析]
∵DE垂直平分AB,∴DA=DB,∴∠DAB=∠B=35°.∵AD是∠BAC的平分线,
∴∠DAC=∠DAB=35°,∴∠C=180°-35°-35°-35°=75°.
11.解:∵DE垂直平分AC,AE=5
cm,
∴DA=DC,AC=2AE=10
cm.
∵△ABD的周长为17
cm,
∴AB+BD+DA=AB+BD+DC=AB+BC=17
cm,
∴△ABC的周长为AB+BC+AC=27
cm.
12.B
13.B [解析]
∵△ABC为等腰三角形,AB,AC为腰,
∴AB=AC,∠ABC=∠ACB,
∴当AD=AE时,根据“SAS”可判定△ABE≌△ACD;
当∠AEB=∠ADC时,根据“AAS”可判定△ABE≌△ACD;
当∠DCB=∠EBC时,∠ABE=∠ACD,根据“ASA”可判定△ABE≌△ACD.
故选B.
14.证明:∵∠BAE=∠DAC,
∴∠BAE+∠CAE=∠DAC+∠CAE,
即∠CAB=∠EAD.
又∵AB=AD,AC=AE,
∴△ABC≌△ADE(SAS),
∴∠C=∠E.
15.证明:延长AD到点G,使DF=DG,连接CG,如图.
∵AD是△ABC的中线,
∴BD=CD.
在△BDF和△CDG中,
∴△BDF≌△CDG(SAS),
∴BF=CG,∠BFD=∠G.
又∵∠AFE=∠BFD,
∴∠AFE=∠G.
∵BF=CG,BF=AC,
∴CG=AC,∴∠G=∠CAF,
∴∠AFE=∠CAF,
∴AE=EF.
同课章节目录
