2021-2022学年湘教版数学七年级上册第4章 图形的认识 单元小结与复习(word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版数学七年级上册第4章 图形的认识 单元小结与复习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 148.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 00:00:00 | ||
图片预览



文档简介
小结与复习
类型之一 立体图形与平面图形
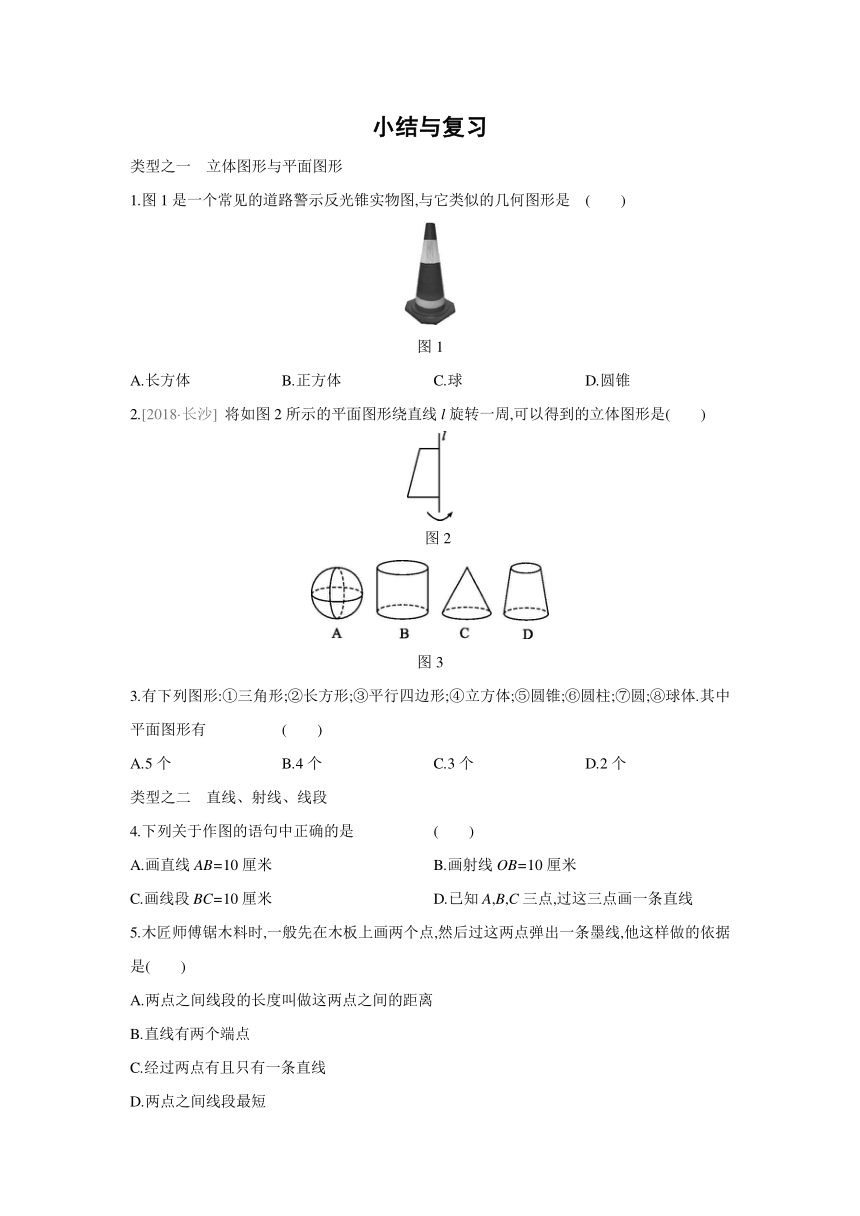
1.图1是一个常见的道路警示反光锥实物图,与它类似的几何图形是
( )
图1
A.长方体
B.正方体
C.球
D.圆锥
2.[2018·长沙]
将如图2所示的平面图形绕直线l旋转一周,可以得到的立体图形是( )
图2
图3
3.有下列图形:①三角形;②长方形;③平行四边形;④立方体;⑤圆锥;⑥圆柱;⑦圆;⑧球体.其中平面图形有
( )
A.5个
B.4个
C.3个
D.2个
类型之二 直线、射线、线段
4.下列关于作图的语句中正确的是
( )
A.画直线AB=10厘米
B.画射线OB=10厘米
C.画线段BC=10厘米
D.已知A,B,C三点,过这三点画一条直线
5.木匠师傅锯木料时,一般先在木板上画两个点,然后过这两点弹出一条墨线,他这样做的依据是( )
A.两点之间线段的长度叫做这两点之间的距离
B.直线有两个端点
C.经过两点有且只有一条直线
D.两点之间线段最短
6.如图4,C为线段AB上一点,AC∶BC=3∶2,D,E分别为AC,AB的中点.若线段DE=2
cm,则AB的长为
( )
图4
A.8
cm
B.12
cm
C.14
cm
D.10
cm
7.如图5,A,B是河l两侧的两个村庄.现要在河l上修建一个抽水站P,使它到两个村庄A,B的距离和最小,小丽认为在图中连接AB,与l的交点就是抽水站P的位置,你认为这里用到的数学基本事实是 .?
图5
8.已知M是直线AB上的点,线段AB=12,AM=2,N是线段MB的中点,画出图形并求线段MN的长.
9.如图6,A,B,C,D四点在同一直线上,M是AB的中点,N是CD的中点.
(1)若MB=3,BC=2,CN=2.5,求AD的长;
(2)若MN=a,BC=b,用a,b表示线段AD的长.
图6
类型之三 角
10.有下列说法:(1)两条射线组成的图形叫做角;(2)一条射线旋转而成的图形叫做角;(3)两边成一条直线的角是平角;(4)平角是一条直线.其中正确的说法有
( )
A.1个
B.2个
C.3个
D.4个
11.已知∠A=40°18',∠B=40°17'30″,∠C=40.18°,则
( )
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠C>∠A>∠B
D.∠A>∠C>∠B
12.已知一个角的余角的补角是这个角的补角的,则这个角的余角的度数是
( )
A.90°
B.60°
C.30°
D.10°
13.已知∠AOB=4∠BOC,若∠BOC=20°,则∠AOC的度数为
( )
A.60°
B.80°或60°
C.80°
D.100°或60°
14.[2019·株洲期末]
如图7,将一副三角尺的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= °.?
图7
15.
图8是一个时钟的钟面,下午1时30分,时钟的分针与时针所夹的角等于 °.?
图8
16.如图9,已知∠AOB=120°,OC,OD分别为∠AOE,∠BOE的平分线,求∠COD的度数.
图9
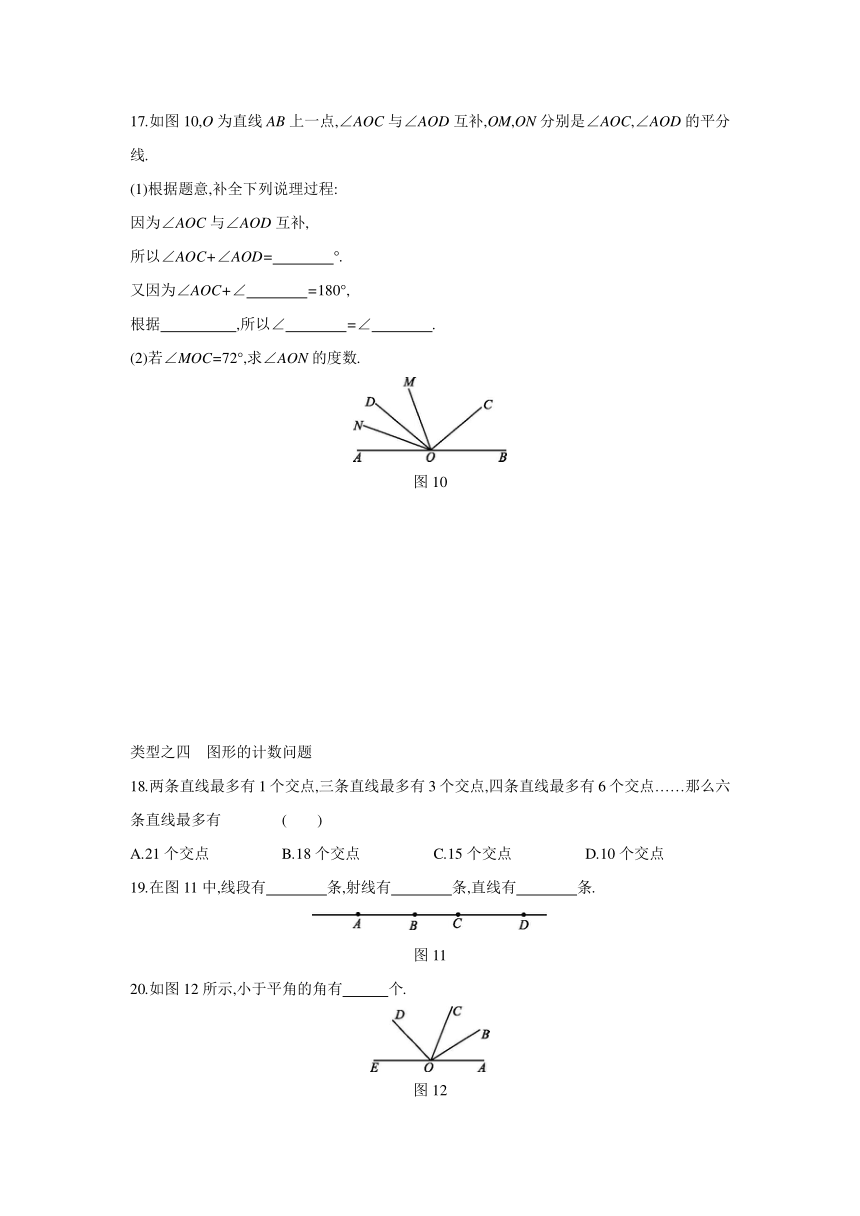
17.如图10,O为直线AB上一点,∠AOC与∠AOD互补,OM,ON分别是∠AOC,∠AOD的平分线.
(1)根据题意,补全下列说理过程:
因为∠AOC与∠AOD互补,
所以∠AOC+∠AOD= °.?
又因为∠AOC+∠ =180°,?
根据 ,所以∠ =∠ .?
(2)若∠MOC=72°,求∠AON的度数.
图10
类型之四 图形的计数问题
18.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么六条直线最多有
( )
A.21个交点
B.18个交点
C.15个交点
D.10个交点
19.在图11中,线段有 条,射线有 条,直线有 条.?
图11
20.如图12所示,小于平角的角有 个.?
图12
类型之五 数学活动
21.如图13,在锐角∠AOB内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角……照此规律,画(n-2)条不同射线,可得锐角 个.?
图13
教师详解详析
1.D [解析]
与常见的道路警示反光锥实物图类似的几何图形是圆锥.
故选D.
2.D [解析]
绕直线l旋转一周,可以得到圆台.故选D.
3.B [解析]
平面图形有①②③⑦,共4个.
4.C
5.C
6.D [解析]
设AB=x,由已知得AC=x,BC=x.
因为D,E分别为AC,AB的中点,
所以AD=x,AE=x,DE=AE-AD.
所以x-x=2,
解得x=10,则AB的长为10
cm.
7.两点之间线段最短
8.解:由于点M的位置不确定,所以需要分情况讨论:
①当点M,B在点A异侧时,如图①:
因为AB=12,AM=2,
所以MB=AB+AM=12+2=14.
因为N是MB的中点,
所以MN=MB.
因为MB=14,
所以MN=×14=7;
②当点M,B在点A同侧时,如图②:
因为AB=12,AM=2,
所以MB=AB-AM=12-2=10.
因为N是MB的中点,
所以MN=MB.
因为MB=10,
所以MN=×10=5.
综上所述,线段MN的长为7或5.
9.解:(1)因为M是AB的中点,N是CD的中点,
所以AB=2MB=6,CD=2CN=5.
所以AD=AB+BC+CD=6+2+5=13.
(2)因为M是AB的中点,N是CD的中点,
所以AM=MB=AB,CN=ND=CD.
因为MN=MB+BC+CN=a,
所以MB+CN=MN-BC=a-b.
所以AB+CD=2MB+2CN=2(a-b).
所以AD=AB+BC+CD=2a-2b+b=2a-b.
10.A
11.A [解析]
因为∠C=40.18°=40°10'48″,
40°18'>40°17'30″>40°10'48″,
所以∠A>∠B>∠C.
12.B [解析]
设这个角为α,则180°-(90°-α)=(180°-α),
所以α=30°.
所以这个角的余角为90°-30°=60°.
故选B.
13.D [解析]
因为∠AOB=4∠BOC,∠BOC=20°,
所以∠AOB=80°.
分两种情况:①当∠BOC的一边OC在∠AOB外部时,则∠AOC=∠AOB+∠BOC=80°+20°=100°;
②当∠BOC的一边OC在∠AOB内部时,则∠AOC=∠AOB-∠BOC=80°-20°=60°.
故选D.
14.30 [解析]
因为∠AOB=∠COD=90°,
∠AOD=150°,
所以∠BOC=∠AOB+∠COD-∠AOD=90°+90°-150°=30°.
故答案为30.
15.135 [解析]
30°×=30°×=135°.
16.[解析]
此题欲求∠COD的度数,可将∠COD转化为∠COE与∠DOE的和,然后再用角平分线的定义,将∠COE与∠DOE分别转化为∠AOE与∠BOE,而∠AOE与∠BOE之和恰好等于∠AOB,从而问题得解.
解:因为OC,OD分别为∠AOE,∠BOE的平分线,
所以∠COE=∠AOE,∠DOE=∠BOE.
所以∠COD=∠COE+∠DOE=∠AOE
+∠BOE=(∠AOE+∠BOE)=∠AOB=×120°=60°.
故∠COD的度数为60°.
17.解:(1)180 BOC 同角的补角相等 AOD
BOC
(2)因为OM是∠AOC的平分线,
所以∠AOC=2∠MOC=2×72°=144°.
因为∠AOC与∠AOD互补,所以∠AOD=36°.
又因为ON平分∠AOD,
所以∠AON=18°.
18.C
19.6 8 1 [解析]
根据线段、射线、直线的定义,计数不妨从端点着手,图中有A,B,C,D四个点,以其中的两点为端点,就有一条线段,以A为左端点的线段有3条;以B为左端点的线段有2条;以C为左端点的线段只有1条,所以图中共有6条线段.
射线只有一个端点,以A,B,C,D为端点的射线分别有2条,由图可知共有8条射线.
直线只有1条.
20.9 [解析]
小于平角的角共有9个:∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE.故答案为9.
21.n(n-1) [解析]
因为在锐角∠AOB内部,画1条射线,可得1+2=3(个)锐角;
在锐角∠AOB内部,画2条射线,可得1+2+3=6(个)锐角;
在锐角∠AOB内部,画3条射线,可得1+2+3+4=10(个)锐角;
…
所以从一个角的内部引出(n-2)条射线所得到的锐角的个数是:
1+2+3+…+(n-1)=n(n-1).
故答案为:n(n-1).
类型之一 立体图形与平面图形
1.图1是一个常见的道路警示反光锥实物图,与它类似的几何图形是
( )
图1
A.长方体
B.正方体
C.球
D.圆锥
2.[2018·长沙]
将如图2所示的平面图形绕直线l旋转一周,可以得到的立体图形是( )
图2
图3
3.有下列图形:①三角形;②长方形;③平行四边形;④立方体;⑤圆锥;⑥圆柱;⑦圆;⑧球体.其中平面图形有
( )
A.5个
B.4个
C.3个
D.2个
类型之二 直线、射线、线段
4.下列关于作图的语句中正确的是
( )
A.画直线AB=10厘米
B.画射线OB=10厘米
C.画线段BC=10厘米
D.已知A,B,C三点,过这三点画一条直线
5.木匠师傅锯木料时,一般先在木板上画两个点,然后过这两点弹出一条墨线,他这样做的依据是( )
A.两点之间线段的长度叫做这两点之间的距离
B.直线有两个端点
C.经过两点有且只有一条直线
D.两点之间线段最短
6.如图4,C为线段AB上一点,AC∶BC=3∶2,D,E分别为AC,AB的中点.若线段DE=2
cm,则AB的长为
( )
图4
A.8
cm
B.12
cm
C.14
cm
D.10
cm
7.如图5,A,B是河l两侧的两个村庄.现要在河l上修建一个抽水站P,使它到两个村庄A,B的距离和最小,小丽认为在图中连接AB,与l的交点就是抽水站P的位置,你认为这里用到的数学基本事实是 .?
图5
8.已知M是直线AB上的点,线段AB=12,AM=2,N是线段MB的中点,画出图形并求线段MN的长.
9.如图6,A,B,C,D四点在同一直线上,M是AB的中点,N是CD的中点.
(1)若MB=3,BC=2,CN=2.5,求AD的长;
(2)若MN=a,BC=b,用a,b表示线段AD的长.
图6
类型之三 角
10.有下列说法:(1)两条射线组成的图形叫做角;(2)一条射线旋转而成的图形叫做角;(3)两边成一条直线的角是平角;(4)平角是一条直线.其中正确的说法有
( )
A.1个
B.2个
C.3个
D.4个
11.已知∠A=40°18',∠B=40°17'30″,∠C=40.18°,则
( )
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠C>∠A>∠B
D.∠A>∠C>∠B
12.已知一个角的余角的补角是这个角的补角的,则这个角的余角的度数是
( )
A.90°
B.60°
C.30°
D.10°
13.已知∠AOB=4∠BOC,若∠BOC=20°,则∠AOC的度数为
( )
A.60°
B.80°或60°
C.80°
D.100°或60°
14.[2019·株洲期末]
如图7,将一副三角尺的直角顶点重合,摆放在桌面上.若∠AOD=150°,则∠BOC= °.?
图7
15.
图8是一个时钟的钟面,下午1时30分,时钟的分针与时针所夹的角等于 °.?
图8
16.如图9,已知∠AOB=120°,OC,OD分别为∠AOE,∠BOE的平分线,求∠COD的度数.
图9
17.如图10,O为直线AB上一点,∠AOC与∠AOD互补,OM,ON分别是∠AOC,∠AOD的平分线.
(1)根据题意,补全下列说理过程:
因为∠AOC与∠AOD互补,
所以∠AOC+∠AOD= °.?
又因为∠AOC+∠ =180°,?
根据 ,所以∠ =∠ .?
(2)若∠MOC=72°,求∠AON的度数.
图10
类型之四 图形的计数问题
18.两条直线最多有1个交点,三条直线最多有3个交点,四条直线最多有6个交点……那么六条直线最多有
( )
A.21个交点
B.18个交点
C.15个交点
D.10个交点
19.在图11中,线段有 条,射线有 条,直线有 条.?
图11
20.如图12所示,小于平角的角有 个.?
图12
类型之五 数学活动
21.如图13,在锐角∠AOB内部,画1条射线,可得3个锐角;画2条不同射线,可得6个锐角;画3条不同射线,可得10个锐角……照此规律,画(n-2)条不同射线,可得锐角 个.?
图13
教师详解详析
1.D [解析]
与常见的道路警示反光锥实物图类似的几何图形是圆锥.
故选D.
2.D [解析]
绕直线l旋转一周,可以得到圆台.故选D.
3.B [解析]
平面图形有①②③⑦,共4个.
4.C
5.C
6.D [解析]
设AB=x,由已知得AC=x,BC=x.
因为D,E分别为AC,AB的中点,
所以AD=x,AE=x,DE=AE-AD.
所以x-x=2,
解得x=10,则AB的长为10
cm.
7.两点之间线段最短
8.解:由于点M的位置不确定,所以需要分情况讨论:
①当点M,B在点A异侧时,如图①:
因为AB=12,AM=2,
所以MB=AB+AM=12+2=14.
因为N是MB的中点,
所以MN=MB.
因为MB=14,
所以MN=×14=7;
②当点M,B在点A同侧时,如图②:
因为AB=12,AM=2,
所以MB=AB-AM=12-2=10.
因为N是MB的中点,
所以MN=MB.
因为MB=10,
所以MN=×10=5.
综上所述,线段MN的长为7或5.
9.解:(1)因为M是AB的中点,N是CD的中点,
所以AB=2MB=6,CD=2CN=5.
所以AD=AB+BC+CD=6+2+5=13.
(2)因为M是AB的中点,N是CD的中点,
所以AM=MB=AB,CN=ND=CD.
因为MN=MB+BC+CN=a,
所以MB+CN=MN-BC=a-b.
所以AB+CD=2MB+2CN=2(a-b).
所以AD=AB+BC+CD=2a-2b+b=2a-b.
10.A
11.A [解析]
因为∠C=40.18°=40°10'48″,
40°18'>40°17'30″>40°10'48″,
所以∠A>∠B>∠C.
12.B [解析]
设这个角为α,则180°-(90°-α)=(180°-α),
所以α=30°.
所以这个角的余角为90°-30°=60°.
故选B.
13.D [解析]
因为∠AOB=4∠BOC,∠BOC=20°,
所以∠AOB=80°.
分两种情况:①当∠BOC的一边OC在∠AOB外部时,则∠AOC=∠AOB+∠BOC=80°+20°=100°;
②当∠BOC的一边OC在∠AOB内部时,则∠AOC=∠AOB-∠BOC=80°-20°=60°.
故选D.
14.30 [解析]
因为∠AOB=∠COD=90°,
∠AOD=150°,
所以∠BOC=∠AOB+∠COD-∠AOD=90°+90°-150°=30°.
故答案为30.
15.135 [解析]
30°×=30°×=135°.
16.[解析]
此题欲求∠COD的度数,可将∠COD转化为∠COE与∠DOE的和,然后再用角平分线的定义,将∠COE与∠DOE分别转化为∠AOE与∠BOE,而∠AOE与∠BOE之和恰好等于∠AOB,从而问题得解.
解:因为OC,OD分别为∠AOE,∠BOE的平分线,
所以∠COE=∠AOE,∠DOE=∠BOE.
所以∠COD=∠COE+∠DOE=∠AOE
+∠BOE=(∠AOE+∠BOE)=∠AOB=×120°=60°.
故∠COD的度数为60°.
17.解:(1)180 BOC 同角的补角相等 AOD
BOC
(2)因为OM是∠AOC的平分线,
所以∠AOC=2∠MOC=2×72°=144°.
因为∠AOC与∠AOD互补,所以∠AOD=36°.
又因为ON平分∠AOD,
所以∠AON=18°.
18.C
19.6 8 1 [解析]
根据线段、射线、直线的定义,计数不妨从端点着手,图中有A,B,C,D四个点,以其中的两点为端点,就有一条线段,以A为左端点的线段有3条;以B为左端点的线段有2条;以C为左端点的线段只有1条,所以图中共有6条线段.
射线只有一个端点,以A,B,C,D为端点的射线分别有2条,由图可知共有8条射线.
直线只有1条.
20.9 [解析]
小于平角的角共有9个:∠AOB,∠AOC,∠AOD,∠BOC,∠BOD,∠BOE,∠COD,∠COE,∠DOE.故答案为9.
21.n(n-1) [解析]
因为在锐角∠AOB内部,画1条射线,可得1+2=3(个)锐角;
在锐角∠AOB内部,画2条射线,可得1+2+3=6(个)锐角;
在锐角∠AOB内部,画3条射线,可得1+2+3+4=10(个)锐角;
…
所以从一个角的内部引出(n-2)条射线所得到的锐角的个数是:
1+2+3+…+(n-1)=n(n-1).
故答案为:n(n-1).
同课章节目录
