2021——2022学年九年级数学湘教版上册第三章图形的相似3.1_3.4.1同步综合练习题 (word版、含解析)
文档属性
| 名称 | 2021——2022学年九年级数学湘教版上册第三章图形的相似3.1_3.4.1同步综合练习题 (word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 147.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 16:03:40 | ||
图片预览


文档简介
3.1——3.4.1 练习题
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列各组线段中,不是成比例线段的是
( )
A.a=3,b=6,c=2,d=4
B.a=1,b=,d=,c=
C.a=4,b=6,c=5,d=10
D.a=2,b=,d=2,c=
2.点B是线段AC的黄金分割点,且AB( )
A.
B.
C.+1
D.-1
3.下列图形中一定是相似形的是
( )
A.两个等边三角形
B.两个菱形
C.两个矩形
D.两个直角三角形
4.如图1,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.若BD=2AD,则
( )
A.=
B.=
C.=
D.=
图1
图2
5.如图2①②中各有两个三角形,其部分边长和角的度数已在图上标注,图②中AB,CD交于点O,对于各图中的两个三角形而言,下列说法正确的是
( )
A.都相似
B.都不相似
C.只有①相似
D.只有②相似
6.如图3,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为
( )
图3
A.6
B.8
C.10
D.12
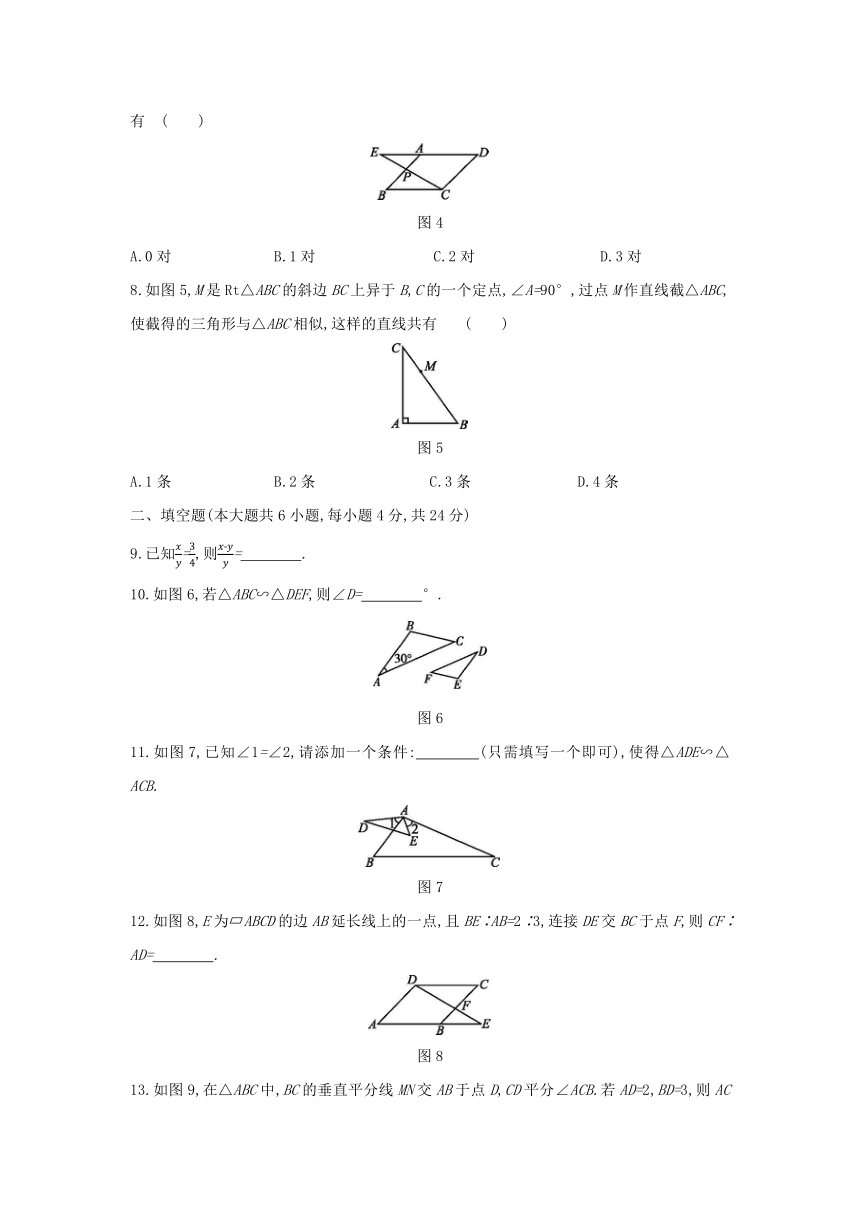
7.如图4,P是?ABCD的边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有
( )
图4
A.0对
B.1对
C.2对
D.3对
8.如图5,M是Rt△ABC的斜边BC上异于B,C的一个定点,∠A=90°,过点M作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有
( )
图5
A.1条
B.2条
C.3条
D.4条
二、填空题(本大题共6小题,每小题4分,共24分)
9.已知=,则= .?
10.如图6,若△ABC∽△DEF,则∠D= °.?
图6
11.如图7,已知∠1=∠2,请添加一个条件: (只需填写一个即可),使得△ADE∽△ACB.?
图7
12.如图8,E为?ABCD的边AB延长线上的一点,且BE∶AB=2∶3,连接DE交BC于点F,则CF∶AD= .?
图8
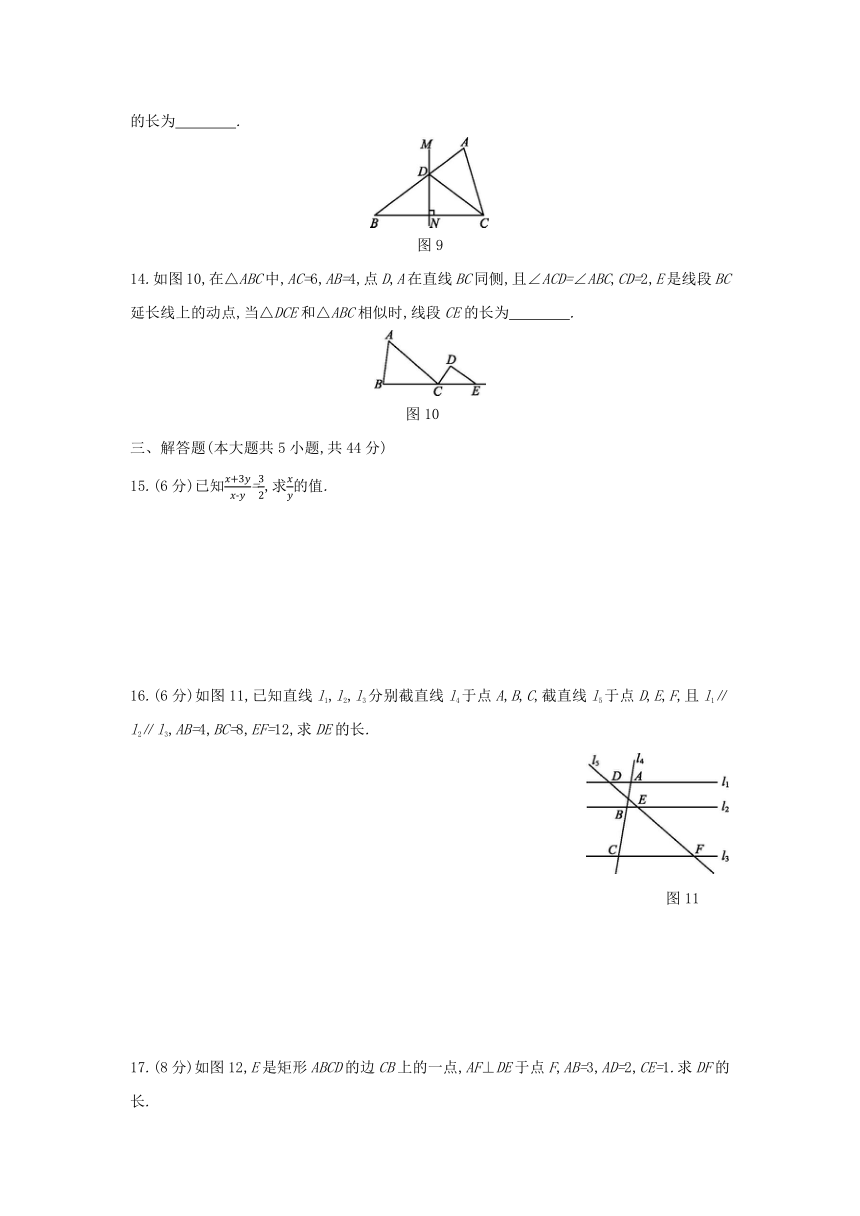
13.如图9,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为 .?
图9
14.如图10,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为 .
图10?
三、解答题(本大题共5小题,共44分)
15.(6分)已知=,求的值.
16.(6分)如图11,已知直线l1,l2,l3分别截直线l4于点A,B,C,截直线l5于点D,E,F,且l1∥l2∥l3,AB=4,BC=8,EF=12,求DE的长.
图11
17.(8分)如图12,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长.
图12
18.(12分)如图13,在?ABCD中,M,N为BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F.
(1)求证:△DFN∽△BEN;
(2)求DF∶AB的值.
图13
19.(12分)如图14,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当E移动到BC的中点时,求证:FE平分∠DFC.
图14
答案
1.C
2.D [解析]∵点B是线段AC的黄金分割点,且AB∵AC=2,∴BC=-1.故选D.
3.A
4.B [解析]∵DE∥BC,∴△ADE∽△ABC.∵BD=2AD,∴===,则=.故选B.
5.A [解析]
图①中,∵∠A=35°,∠B=75°,
∴∠C=180°-∠A-∠B=70°.
∵∠E=75°,∠F=70°,∴∠B=∠E,∠C=∠F,∴△ABC∽△DEF;图②中,∵OA=4,OD=3,OC=8,OB=6,∴=.
又∵∠AOC=∠DOB,∴△AOC∽△DOB.
6.C [解析]∵DE∥BC,∴∠ADE=∠B.∵∠ADE=∠EFC,∴∠B=∠EFC,∴BD∥EF.又∵DE∥BF,∴四边形BDEF为平行四边形,∴DE=BF.∵DE∥BC,∴△ADE∽△ABC,∴===,∴BC=DE,∴CF=BC-BF=DE=6,∴DE=10.故选C.
7.D [解析]
由题意,得△EAP∽△EDC,△EAP∽△CBP,∴△EDC∽△CBP,∴共有3对相似三角形.故选D.
8.C [解析]
如图,分别过点M作△ABC三边的垂线l1,l2,l3,易证此时分别形成的三角形均与原三角形相似,所以共有3条.
9.- 10.30
11.∠B=∠E(答案不唯一)
12. [解析]
由题意可知CD∥AE,CD=AB,∴△CDF∽△BEF,∴=.
∵==,∴=,∴=.
∵AD=BC,∴==.
13. [解析]∵BC的垂直平分线MN交AB于点D,∴BD=CD,
∴∠B=∠DCB.
∵AD=2,BD=3,∴AB=AD+BD=5.
∵CD平分∠ACB,∴∠ACD=∠DCB,
∴∠ACD=∠B.
又∵∠A=∠A,∴△ACD∽△ABC,
∴=,
∴AC2=AD·AB=2×5=10,∴AC=.
故答案为.
14.或3 [解析]∵∠ACD+∠DCE=∠B+∠A,∠ACD=∠B,∴∠DCE=∠A,
∴∠A与∠DCE是对应角,
∴△DCE和△ABC相似有两种情况:
(1)若△BAC∽△ECD,有=,
即=,∴CE=;
(2)若△BAC∽△DCE,有=,
即=,
∴CE=3.
综上所述,CE的长为或3.
15.解:∵=,
∴2x+6y=3x-3y,
∴x=9y,则=9.
16.解:∵l1∥l2∥l3,
∴=,即=,
解得DE=6.
故DE的长为6.
17.解:∵四边形ABCD是矩形,
∴DC=AB=3,∠ADC=∠C=90°,
∴∠ADE+∠EDC=90°.
∵CE=1,DC=3,
∴DE==.
∵AF⊥DE,
∴∠AFD=90°,
∴∠AFD=∠C,∠ADF+∠DAF=90°,
∴∠EDC=∠DAF,
∴△EDC∽△DAF,
∴=,即=,
∴FD=,即DF的长度为.
18.解:(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴△DFN∽△BEN.
(2)由(1)知△DFN∽△BEN,同理可得△DMC∽△BME.
∵M,N为BD的三等分点,
∴DF∶BE=DN∶BN=1∶2,BE∶DC=BM∶DM=1∶2.
又∵AB=DC,
∴DF∶AB=1∶4=.
19.证明:(1)∵AB=AC,∴∠B=∠C.
∵∠BDE=180°-∠B-∠DEB,
∠CEF=180°-∠DEF-∠DEB,
∠DEF=∠B,
∴∠BDE=∠CEF,
∴△BDE∽△CEF.
(2)由(1)得△BDE∽△CEF,
∴=.
∵E是BC的中点,∴BE=CE,
∴=,∴=.
又∵∠DEF=∠B=∠C,
∴△DEF∽△ECF,
∴∠DFE=∠CFE,
∴FE平分∠DFC.
一、选择题(本大题共8小题,每小题4分,共32分)
1.下列各组线段中,不是成比例线段的是
( )
A.a=3,b=6,c=2,d=4
B.a=1,b=,d=,c=
C.a=4,b=6,c=5,d=10
D.a=2,b=,d=2,c=
2.点B是线段AC的黄金分割点,且AB
A.
B.
C.+1
D.-1
3.下列图形中一定是相似形的是
( )
A.两个等边三角形
B.两个菱形
C.两个矩形
D.两个直角三角形
4.如图1,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.若BD=2AD,则
( )
A.=
B.=
C.=
D.=
图1
图2
5.如图2①②中各有两个三角形,其部分边长和角的度数已在图上标注,图②中AB,CD交于点O,对于各图中的两个三角形而言,下列说法正确的是
( )
A.都相似
B.都不相似
C.只有①相似
D.只有②相似
6.如图3,在△ABC中,DE∥BC,∠ADE=∠EFC,AD∶BD=5∶3,CF=6,则DE的长为
( )
图3
A.6
B.8
C.10
D.12
7.如图4,P是?ABCD的边AB上的一点,射线CP交DA的延长线于点E,则图中相似的三角形有
( )
图4
A.0对
B.1对
C.2对
D.3对
8.如图5,M是Rt△ABC的斜边BC上异于B,C的一个定点,∠A=90°,过点M作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有
( )
图5
A.1条
B.2条
C.3条
D.4条
二、填空题(本大题共6小题,每小题4分,共24分)
9.已知=,则= .?
10.如图6,若△ABC∽△DEF,则∠D= °.?
图6
11.如图7,已知∠1=∠2,请添加一个条件: (只需填写一个即可),使得△ADE∽△ACB.?
图7
12.如图8,E为?ABCD的边AB延长线上的一点,且BE∶AB=2∶3,连接DE交BC于点F,则CF∶AD= .?
图8
13.如图9,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为 .?
图9
14.如图10,在△ABC中,AC=6,AB=4,点D,A在直线BC同侧,且∠ACD=∠ABC,CD=2,E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为 .
图10?
三、解答题(本大题共5小题,共44分)
15.(6分)已知=,求的值.
16.(6分)如图11,已知直线l1,l2,l3分别截直线l4于点A,B,C,截直线l5于点D,E,F,且l1∥l2∥l3,AB=4,BC=8,EF=12,求DE的长.
图11
17.(8分)如图12,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1.求DF的长.
图12
18.(12分)如图13,在?ABCD中,M,N为BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F.
(1)求证:△DFN∽△BEN;
(2)求DF∶AB的值.
图13
19.(12分)如图14,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF;
(2)当E移动到BC的中点时,求证:FE平分∠DFC.
图14
答案
1.C
2.D [解析]∵点B是线段AC的黄金分割点,且AB
3.A
4.B [解析]∵DE∥BC,∴△ADE∽△ABC.∵BD=2AD,∴===,则=.故选B.
5.A [解析]
图①中,∵∠A=35°,∠B=75°,
∴∠C=180°-∠A-∠B=70°.
∵∠E=75°,∠F=70°,∴∠B=∠E,∠C=∠F,∴△ABC∽△DEF;图②中,∵OA=4,OD=3,OC=8,OB=6,∴=.
又∵∠AOC=∠DOB,∴△AOC∽△DOB.
6.C [解析]∵DE∥BC,∴∠ADE=∠B.∵∠ADE=∠EFC,∴∠B=∠EFC,∴BD∥EF.又∵DE∥BF,∴四边形BDEF为平行四边形,∴DE=BF.∵DE∥BC,∴△ADE∽△ABC,∴===,∴BC=DE,∴CF=BC-BF=DE=6,∴DE=10.故选C.
7.D [解析]
由题意,得△EAP∽△EDC,△EAP∽△CBP,∴△EDC∽△CBP,∴共有3对相似三角形.故选D.
8.C [解析]
如图,分别过点M作△ABC三边的垂线l1,l2,l3,易证此时分别形成的三角形均与原三角形相似,所以共有3条.
9.- 10.30
11.∠B=∠E(答案不唯一)
12. [解析]
由题意可知CD∥AE,CD=AB,∴△CDF∽△BEF,∴=.
∵==,∴=,∴=.
∵AD=BC,∴==.
13. [解析]∵BC的垂直平分线MN交AB于点D,∴BD=CD,
∴∠B=∠DCB.
∵AD=2,BD=3,∴AB=AD+BD=5.
∵CD平分∠ACB,∴∠ACD=∠DCB,
∴∠ACD=∠B.
又∵∠A=∠A,∴△ACD∽△ABC,
∴=,
∴AC2=AD·AB=2×5=10,∴AC=.
故答案为.
14.或3 [解析]∵∠ACD+∠DCE=∠B+∠A,∠ACD=∠B,∴∠DCE=∠A,
∴∠A与∠DCE是对应角,
∴△DCE和△ABC相似有两种情况:
(1)若△BAC∽△ECD,有=,
即=,∴CE=;
(2)若△BAC∽△DCE,有=,
即=,
∴CE=3.
综上所述,CE的长为或3.
15.解:∵=,
∴2x+6y=3x-3y,
∴x=9y,则=9.
16.解:∵l1∥l2∥l3,
∴=,即=,
解得DE=6.
故DE的长为6.
17.解:∵四边形ABCD是矩形,
∴DC=AB=3,∠ADC=∠C=90°,
∴∠ADE+∠EDC=90°.
∵CE=1,DC=3,
∴DE==.
∵AF⊥DE,
∴∠AFD=90°,
∴∠AFD=∠C,∠ADF+∠DAF=90°,
∴∠EDC=∠DAF,
∴△EDC∽△DAF,
∴=,即=,
∴FD=,即DF的长度为.
18.解:(1)证明:∵四边形ABCD是平行四边形,
∴DC∥AB,
∴△DFN∽△BEN.
(2)由(1)知△DFN∽△BEN,同理可得△DMC∽△BME.
∵M,N为BD的三等分点,
∴DF∶BE=DN∶BN=1∶2,BE∶DC=BM∶DM=1∶2.
又∵AB=DC,
∴DF∶AB=1∶4=.
19.证明:(1)∵AB=AC,∴∠B=∠C.
∵∠BDE=180°-∠B-∠DEB,
∠CEF=180°-∠DEF-∠DEB,
∠DEF=∠B,
∴∠BDE=∠CEF,
∴△BDE∽△CEF.
(2)由(1)得△BDE∽△CEF,
∴=.
∵E是BC的中点,∴BE=CE,
∴=,∴=.
又∵∠DEF=∠B=∠C,
∴△DEF∽△ECF,
∴∠DFE=∠CFE,
∴FE平分∠DFC.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
