2021-2022学年湘教版八年级数学上册第4章一元一次不等式(组) 类型练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版八年级数学上册第4章一元一次不等式(组) 类型练习题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 99.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 11:32:26 | ||
图片预览


文档简介
第4章 一元一次不等式(组)
类型之一 不等式及其基本性质
1.有下列式子:①a+b=b+a;②-2>-5;③x≥-1;④y-4<1;⑤2m≥n;⑥2x-3.其中是不等式的有( )
A.2个
B.3个
C.4个
D.5个
2.[2020·贵港]
如果a( )
A.a+cB.ac>bc
C.ac+1>bc+1
D.ac2>bc2
3.“x的2倍与x的相反数的差不小于1”,用不等式表示为
( )
A.2x-x≥1
B.2x-(-x)≥1
C.2x-x>1
D.2x-(-x)>1
4.若a”“<”或“=”填空)?
类型之二 一元一次不等式的解法
5.[2020·长春]
不等式x+2≥3的解集在数轴上的表示正确的是
( )
图1
6.已知不等式-2x+a≥2的解集是x≤-1,则a的值是
( )
A.0
B.2
C.-2
D.-4
7.[2020·锦州]
不等式>1的解集为 .?
8.已知关于x的不等式2x9.解不等式:+≤1.
类型之三 一元一次不等式组的解法
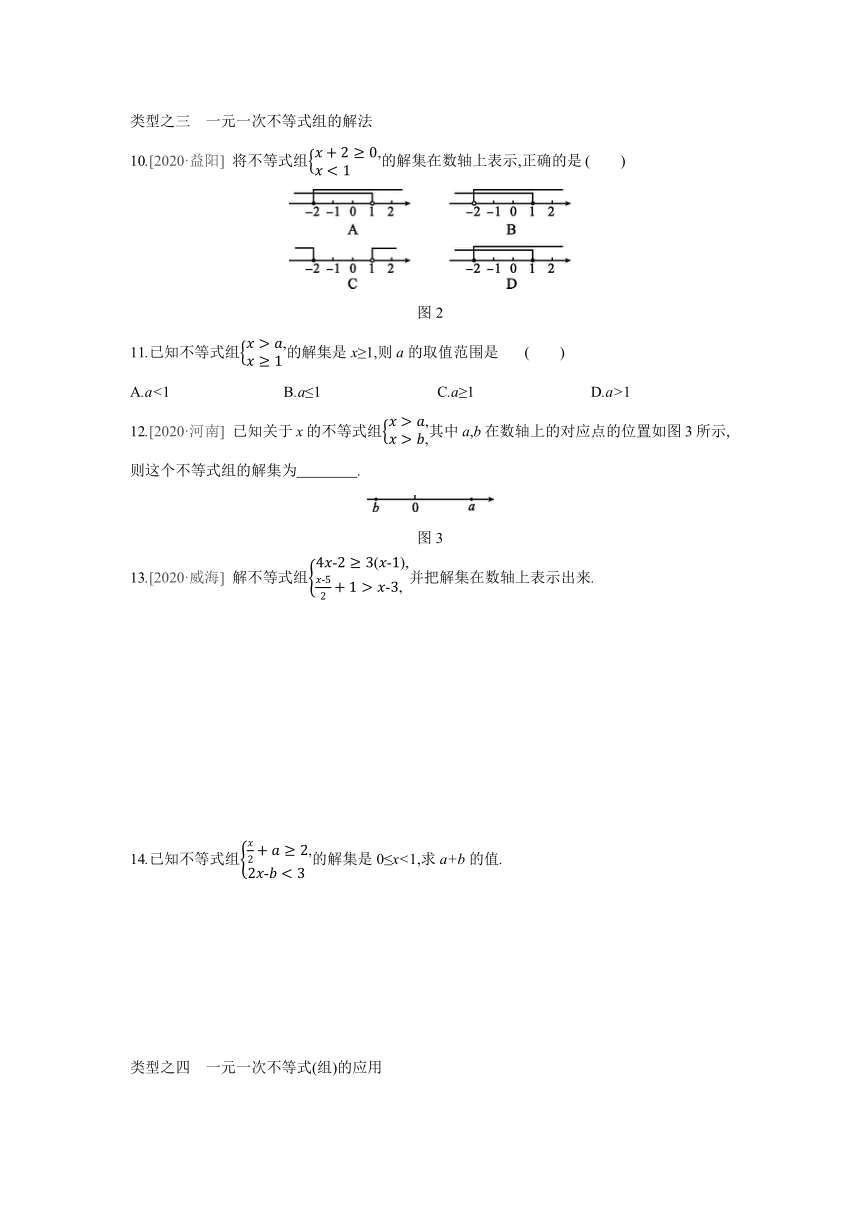
10.[2020·益阳]
将不等式组的解集在数轴上表示,正确的是
( )
图2
11.已知不等式组的解集是x≥1,则a的取值范围是
( )
A.a<1
B.a≤1
C.a≥1
D.a>1
12.[2020·河南]
已知关于x的不等式组其中a,b在数轴上的对应点的位置如图3所示,则这个不等式组的解集为 .?
图3
13.[2020·威海]
解不等式组并把解集在数轴上表示出来.
14.已知不等式组的解集是0≤x<1,求a+b的值.
类型之四 一元一次不等式(组)的应用
15.某次知识竞赛共有20题,答对一题得10分,答错或不答一题都扣5分.小华得分要超过120分,则她至少要答对
( )
A.13题
B.14题
C.15题
D.16题
16.[2019·怀化]
为了落实精准扶贫政策,某单位针对某山区贫困村的实际情况,特向该村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只.若每户发放母羊5只,则多出17只母羊;若每户发放母羊7只,则有一户可分得母羊但不足3只.这批种羊共有
( )
A.55只
B.72只
C.83只
D.89只
17.一位老师说,他班里一半的学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足6名学生在操场上踢足球,则这个班的学生有 人.?
18.[2020·邵阳]
2020年5月,全国“两会”召开以后,应势复苏的“地摊经济”带来了市场新活力.小丹准备购进A,B两种类型的便携式风扇到地摊一条街出售.已知2台A型风扇和5台B型风扇进价共100元,3台A型风扇和2台B型风扇进价共62元.
(1)求A型风扇、B型风扇进货的单价各是多少;
(2)小丹准备购进这两种风扇共100台,根据市场调查发现,A型风扇的销售情况比B型风扇好,小丹准备多购进A型风扇,但数量不超过B型风扇数量的3倍,购进A,B两种风扇的总金额不超过1170元.根据以上信息,小丹共有哪些进货方案?
类型之五 数学活动
19.某旅游景点门票是50元,凡购买5张门票以上(含5张),景点售票处推出两种优惠销售方案,第一种方案:3张按原价,其余按原价的七折付款;第二种方案:全部按原价的八折付款.
(1)购买门票张数在什么范围选用第二种方案合算?
(2)若购买10张门票,则选用哪种方案费用较少?请说明理由.
20.阅读材料:
解分式不等式:<0.
解:根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为
①或②
解不等式组①,得无解;
解不等式组②,得-2所以原不等式的解集是-2请仿照上述方法解下列分式不等式:
(1)≤0;(2)>0.
答案
1.C [解析]
②③④⑤是不等式.
2.D [解析]
由a由abc,原变形正确,故B选项不符合题意;
由abc+1,原变形正确,故C选项不符合题意;
由a3.B
4.< > [解析]
若a-b,所以-a+1>-b+1.
5.D [解析]
x+2≥3,x≥3-2,即x≥1.故选D.
6.A [解析]
移项,得-2x≥2-a.两边都除以-2,得x≤.∵x≤-1,∴=-1,解得a=0.故选A.
7.x>-2 [解析]
∵>1,
∴4+x>2,
∴x>-2.
故答案为x>-2.
8.42x9.解:去分母,得2x+3(x-3)≤6.
去括号,得2x+3x-9≤6.
移项、
合并同类项,得5x≤15.
两边都除以5,得x≤3.
10.A [解析]
解不等式x+2≥0,得x≥-2,
又x<1,
∴不等式组的解集为-2≤x<1.
把不等式组的解集表示在数轴上如图所示.
故选A.
11.A
12.x>a [解析]
∵b<0∴关于x的不等式组的解集为x>a.
故答案为x>a.
13.解:
解不等式①,得x≥-1;
解不等式②,得x<3.
∴原不等式组的解集为-1≤x<3.
把解集表示在数轴上如图所示.
14.解:由+a≥2,得x≥4-2a.
由2x-b<3,得x<.
故原不等式组的解集为4-2a≤x<.
又∵0≤x<1,∴4-2a=0,=1,
解得a=2,b=-1,∴a+b=1.
15.C [解析]
设她要答对x道题.由题意,得10x+(-5)×(20-x)>120,10x-100+5x>120,15x>220,解得x>.因为x必须为整数,所以她至少要答对15道题.
16.C [解析]
设该村共有x户,则母羊共有(5x+17)只.由题意知,解得17.28 [解析]
设这个班的学生有x人.由题意,得x-x-x-x<6,
解得x<56.
又∵x为2,4,7的公倍数,
∴这个班的学生有28人.
18.解:(1)设A型风扇进货的单价是x元/台,B型风扇进货的单价是y元/台.
由题意,得
解得
答:A型风扇进货的单价是10元/台,B型风扇进货的单价是16元/台.
(2)设购进A型风扇m台,则购进B型风扇(100-m)台.
由题意,得
解得71≤m≤75.
又∵m为正整数,
∴m可以取72,73,74,75,
∴小丹共有4种进货方案,方案1:购进A型风扇72台,B型风扇28台;方案2:购进A型风扇73台,B型风扇27台;方案3:购进A型风扇74台,B型风扇26台;方案4:购进A型风扇75台,B型风扇25台.
19.解:(1)设购买门票x张.由题意,得
解得5≤x<9.
又∵x只能为整数,
∴x的值为5或6或7或8.
答:购买门票张数为5或6或7或8时选用第二种方案合算.
(2)若购买10张门票,则选用第一种方案费用较少.
理由:
第一种方案所需费用为50×3+50×0.7×(10-3)=395(元),
第二种方案所需费用为50×0.8×10=400(元).
显然,第一种方案费用较少.因此购买10张门票选择第一种方案费用较少.
20.解:(1)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为①或②
解不等式组①,得无解;
解不等式组②,得-2.5所以原不等式的解集是-2.5(2)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为①或②
解不等式组①,得x>3.
解不等式组②,得x<-2.
所以原不等式的解集是x>3或x<-2.
类型之一 不等式及其基本性质
1.有下列式子:①a+b=b+a;②-2>-5;③x≥-1;④y-4<1;⑤2m≥n;⑥2x-3.其中是不等式的有( )
A.2个
B.3个
C.4个
D.5个
2.[2020·贵港]
如果a
A.a+c
C.ac+1>bc+1
D.ac2>bc2
3.“x的2倍与x的相反数的差不小于1”,用不等式表示为
( )
A.2x-x≥1
B.2x-(-x)≥1
C.2x-x>1
D.2x-(-x)>1
4.若a
类型之二 一元一次不等式的解法
5.[2020·长春]
不等式x+2≥3的解集在数轴上的表示正确的是
( )
图1
6.已知不等式-2x+a≥2的解集是x≤-1,则a的值是
( )
A.0
B.2
C.-2
D.-4
7.[2020·锦州]
不等式>1的解集为 .?
8.已知关于x的不等式2x
类型之三 一元一次不等式组的解法
10.[2020·益阳]
将不等式组的解集在数轴上表示,正确的是
( )
图2
11.已知不等式组的解集是x≥1,则a的取值范围是
( )
A.a<1
B.a≤1
C.a≥1
D.a>1
12.[2020·河南]
已知关于x的不等式组其中a,b在数轴上的对应点的位置如图3所示,则这个不等式组的解集为 .?
图3
13.[2020·威海]
解不等式组并把解集在数轴上表示出来.
14.已知不等式组的解集是0≤x<1,求a+b的值.
类型之四 一元一次不等式(组)的应用
15.某次知识竞赛共有20题,答对一题得10分,答错或不答一题都扣5分.小华得分要超过120分,则她至少要答对
( )
A.13题
B.14题
C.15题
D.16题
16.[2019·怀化]
为了落实精准扶贫政策,某单位针对某山区贫困村的实际情况,特向该村提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户1只.若每户发放母羊5只,则多出17只母羊;若每户发放母羊7只,则有一户可分得母羊但不足3只.这批种羊共有
( )
A.55只
B.72只
C.83只
D.89只
17.一位老师说,他班里一半的学生在学数学,四分之一的学生在学音乐,七分之一的学生在学外语,还剩不足6名学生在操场上踢足球,则这个班的学生有 人.?
18.[2020·邵阳]
2020年5月,全国“两会”召开以后,应势复苏的“地摊经济”带来了市场新活力.小丹准备购进A,B两种类型的便携式风扇到地摊一条街出售.已知2台A型风扇和5台B型风扇进价共100元,3台A型风扇和2台B型风扇进价共62元.
(1)求A型风扇、B型风扇进货的单价各是多少;
(2)小丹准备购进这两种风扇共100台,根据市场调查发现,A型风扇的销售情况比B型风扇好,小丹准备多购进A型风扇,但数量不超过B型风扇数量的3倍,购进A,B两种风扇的总金额不超过1170元.根据以上信息,小丹共有哪些进货方案?
类型之五 数学活动
19.某旅游景点门票是50元,凡购买5张门票以上(含5张),景点售票处推出两种优惠销售方案,第一种方案:3张按原价,其余按原价的七折付款;第二种方案:全部按原价的八折付款.
(1)购买门票张数在什么范围选用第二种方案合算?
(2)若购买10张门票,则选用哪种方案费用较少?请说明理由.
20.阅读材料:
解分式不等式:<0.
解:根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为
①或②
解不等式组①,得无解;
解不等式组②,得-2
(1)≤0;(2)>0.
答案
1.C [解析]
②③④⑤是不等式.
2.D [解析]
由a
由a
由a
4.< > [解析]
若a
5.D [解析]
x+2≥3,x≥3-2,即x≥1.故选D.
6.A [解析]
移项,得-2x≥2-a.两边都除以-2,得x≤.∵x≤-1,∴=-1,解得a=0.故选A.
7.x>-2 [解析]
∵>1,
∴4+x>2,
∴x>-2.
故答案为x>-2.
8.4
去括号,得2x+3x-9≤6.
移项、
合并同类项,得5x≤15.
两边都除以5,得x≤3.
10.A [解析]
解不等式x+2≥0,得x≥-2,
又x<1,
∴不等式组的解集为-2≤x<1.
把不等式组的解集表示在数轴上如图所示.
故选A.
11.A
12.x>a [解析]
∵b<0
故答案为x>a.
13.解:
解不等式①,得x≥-1;
解不等式②,得x<3.
∴原不等式组的解集为-1≤x<3.
把解集表示在数轴上如图所示.
14.解:由+a≥2,得x≥4-2a.
由2x-b<3,得x<.
故原不等式组的解集为4-2a≤x<.
又∵0≤x<1,∴4-2a=0,=1,
解得a=2,b=-1,∴a+b=1.
15.C [解析]
设她要答对x道题.由题意,得10x+(-5)×(20-x)>120,10x-100+5x>120,15x>220,解得x>.因为x必须为整数,所以她至少要答对15道题.
16.C [解析]
设该村共有x户,则母羊共有(5x+17)只.由题意知,解得
设这个班的学生有x人.由题意,得x-x-x-x<6,
解得x<56.
又∵x为2,4,7的公倍数,
∴这个班的学生有28人.
18.解:(1)设A型风扇进货的单价是x元/台,B型风扇进货的单价是y元/台.
由题意,得
解得
答:A型风扇进货的单价是10元/台,B型风扇进货的单价是16元/台.
(2)设购进A型风扇m台,则购进B型风扇(100-m)台.
由题意,得
解得71≤m≤75.
又∵m为正整数,
∴m可以取72,73,74,75,
∴小丹共有4种进货方案,方案1:购进A型风扇72台,B型风扇28台;方案2:购进A型风扇73台,B型风扇27台;方案3:购进A型风扇74台,B型风扇26台;方案4:购进A型风扇75台,B型风扇25台.
19.解:(1)设购买门票x张.由题意,得
解得5≤x<9.
又∵x只能为整数,
∴x的值为5或6或7或8.
答:购买门票张数为5或6或7或8时选用第二种方案合算.
(2)若购买10张门票,则选用第一种方案费用较少.
理由:
第一种方案所需费用为50×3+50×0.7×(10-3)=395(元),
第二种方案所需费用为50×0.8×10=400(元).
显然,第一种方案费用较少.因此购买10张门票选择第一种方案费用较少.
20.解:(1)根据实数的除法法则:同号两数相除得正数,异号两数相除得负数,因此,原不等式可转化为①或②
解不等式组①,得无解;
解不等式组②,得-2.5
解不等式组①,得x>3.
解不等式组②,得x<-2.
所以原不等式的解集是x>3或x<-2.
同课章节目录
