1.4.1.1空间中点、直线和平面的向量表示课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(15张PPT)
文档属性
| 名称 | 1.4.1.1空间中点、直线和平面的向量表示课件-2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 20:44:26 | ||
图片预览



文档简介
人教A版(2019)选择性必修第一册
第一章 空间向量与立体几何
1.4.1 空间中点、线、面的向量表示(1)
平面向量
空间向量
代数运算
推广
建系
一.复习回顾
空间向量解决了哪些几何问题?
问题
距离问题
夹角问题
平行、垂直问题
二.探究新知
几何中
点
线
面
向量中
?
?
?
点、线、面是空间的基本图形,点、线段、平面图形是组成空间几何体的基本元素.因此,为了用空间向量研究立体几何问题,首先要用向量表示空间中的点、线、面.
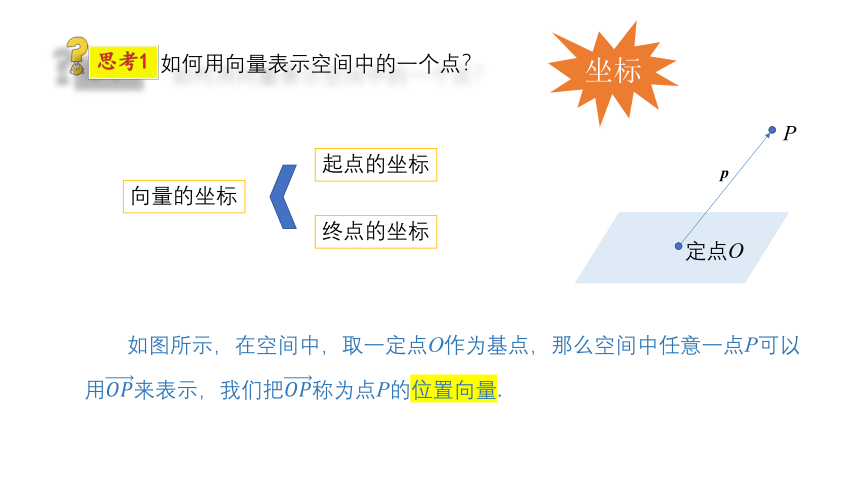
如何用向量表示空间中的一个点?
思考1
定点O
P
p
如图所示,在空间中,取一定点O作为基点,那么空间中任意一点P可以用????????来表示,我们把????????称为点P的位置向量.
?
向量的坐标
起点的坐标
终点的坐标
坐标
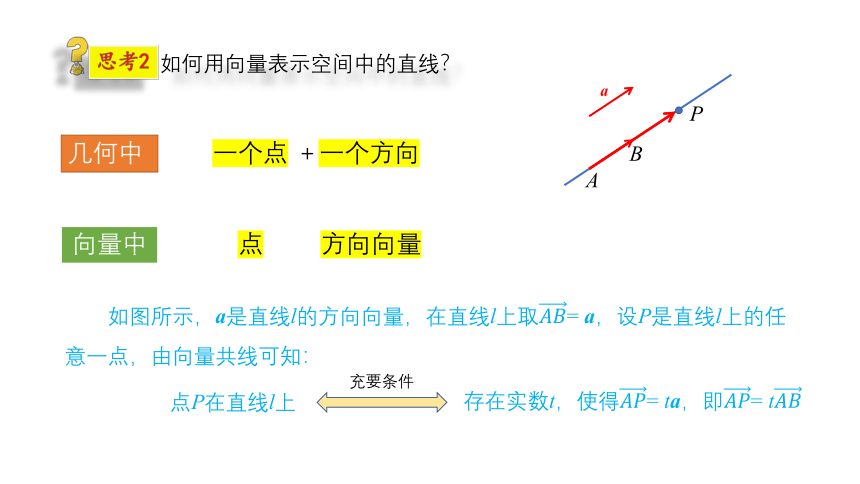
如何用向量表示空间中的直线?
思考2
P
几何中
向量中
点
方向向量
a
A
B
如图所示,a是直线l的方向向量,在直线l上取????????= a,设P是直线l上的任意一点,由向量共线可知:
?
点P在直线l上
存在实数t,使得????????= ta,即????????= t????????
?
充要条件
一个点
一个方向
+
????????= t????????
?
P
a
A
B
进一步地,如图,取定空间中的任意一点O,
O
可以得到:P在直线l上的充要条件是存在实数t,使
????????=????????+t???????? ①
或????????=????????+t???? ②
?
① ②式称为空间直线l的向量表示.
由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
你能证明这个结论吗?
????=????????+????
?
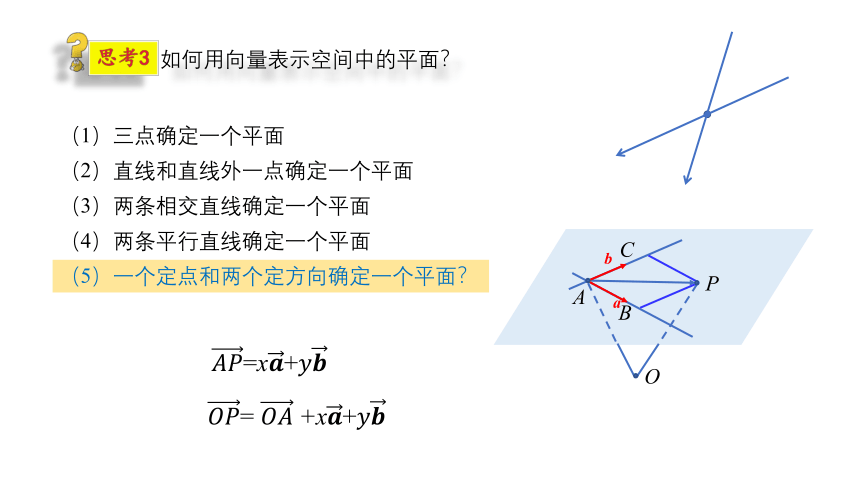
如何用向量表示空间中的平面?
思考3
(1)三点确定一个平面
(2)直线和直线外一点确定一个平面
(3)两条相交直线确定一个平面
(4)两条平行直线确定一个平面
(5)一个定点和两个定方向确定一个平面?
a
b
????????=x????+????????
?
????????= ?????????+x????+????????
?
B
C
P
A
O
????
?
l
如何用向量表示空间中的平面?
思考
(5)一个定点和两个定方向确定一个平面?
(6)一个定点和一个定方向确定一个平面?
A
P
平面????过点A,且????⊥?????????是唯一的
?
a
直线l⊥????,取直线l的方向向量a,称向量a为平面????的法向量.
可以表示为集合{P∣????·????????=0}
?
如果另有一条直线m⊥????,在直线m上任取向量b , b与a有什么关系?
?
三.典例剖析
例1.已知长方体ABCD-?A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
x
y
z
D
A
B
C
D1
A1
B1
C1
M
(1)因为y轴垂直于平面BCC1B1,所以n1=(0,1,0)是平面BCC1B1的一个法向量.
解:
(2)因为AB=4, BC=3, CC1 =2,M是AB的中点,所以M,C,A的坐标分别为(3,2,0),(0,4,0),(3,0,2).因此
????????=(-3,2,0), ????????1=(0,-2,2),
设n2=(x,y,z)是平面MCA1的一个法向量,则
n2⊥ ????????,n2⊥????????1,
所以????2??????????=?3????+2????=0????2?????????1=?2????+2????=0 解得????=23????????=??
令z=3,则x=2,y=3,所以n2=(2,3,3)是平面MCA1的一个法向量.
?
归纳求解平面法向量的一般步骤:
(1)根据立体几何中线面垂直的判定定理得到法向量;
(2)根据向量运算的坐标表示得到两个三元一次方程,联立方程组;
(3)根据三元一次不定方程组,得到一个法向量.
设向量
选向量
列方程组
解方程组
赋非零值
得结论
练习
练习3.在长方体ABCD-?A1B1C1D1中,AB=4,BC=3,CC1 =2,以D为原点,以{13????????, 14????????, 12????????}为空间的一个单位正交基底,建立空间直角坐标系Oxyz,求平面ACD1的一个法向量.
?
x
y
z
D
A
B
C
D1
A1
B1
C1
1、判断下列命题是否正确
(1)零向量不能作为直线的方向向量和平面的法向量。 ( )
(2)若v是直线l的方向向量,则λv(λ∈R)也是直线l的方向向量。 ( )
(3)在空间直角坐标系中,j=(0,0,1)是坐标平面Oxy的一个法向量。 ( )
2、在平行六面体ABCD-A1B1C1D1中,????????=a , ????????=b , ????????1=c ,O是BD1与B1D的交点.
以{a,b,c}为空间的一个基底,求直线OA的一个方向向量.
?
练习
四.课堂小结
1、空间中点、直线和平面的向量表示
点→点+位置向量
线→点+方向向量
平面→点+法向量
设向量
选向量
列方程组
解方程组
赋非零值
得结论
2、归纳求平面法向量的步骤:
五.作业布置
课本P29 练习 3
课本P41 习题1.4 第1题
第一章 空间向量与立体几何
1.4.1 空间中点、线、面的向量表示(1)
平面向量
空间向量
代数运算
推广
建系
一.复习回顾
空间向量解决了哪些几何问题?
问题
距离问题
夹角问题
平行、垂直问题
二.探究新知
几何中
点
线
面
向量中
?
?
?
点、线、面是空间的基本图形,点、线段、平面图形是组成空间几何体的基本元素.因此,为了用空间向量研究立体几何问题,首先要用向量表示空间中的点、线、面.
如何用向量表示空间中的一个点?
思考1
定点O
P
p
如图所示,在空间中,取一定点O作为基点,那么空间中任意一点P可以用????????来表示,我们把????????称为点P的位置向量.
?
向量的坐标
起点的坐标
终点的坐标
坐标
如何用向量表示空间中的直线?
思考2
P
几何中
向量中
点
方向向量
a
A
B
如图所示,a是直线l的方向向量,在直线l上取????????= a,设P是直线l上的任意一点,由向量共线可知:
?
点P在直线l上
存在实数t,使得????????= ta,即????????= t????????
?
充要条件
一个点
一个方向
+
????????= t????????
?
P
a
A
B
进一步地,如图,取定空间中的任意一点O,
O
可以得到:P在直线l上的充要条件是存在实数t,使
????????=????????+t???????? ①
或????????=????????+t???? ②
?
① ②式称为空间直线l的向量表示.
由此可知,空间任意直线由直线上一点及直线的方向向量唯一确定.
你能证明这个结论吗?
????=????????+????
?
如何用向量表示空间中的平面?
思考3
(1)三点确定一个平面
(2)直线和直线外一点确定一个平面
(3)两条相交直线确定一个平面
(4)两条平行直线确定一个平面
(5)一个定点和两个定方向确定一个平面?
a
b
????????=x????+????????
?
????????= ?????????+x????+????????
?
B
C
P
A
O
????
?
l
如何用向量表示空间中的平面?
思考
(5)一个定点和两个定方向确定一个平面?
(6)一个定点和一个定方向确定一个平面?
A
P
平面????过点A,且????⊥?????????是唯一的
?
a
直线l⊥????,取直线l的方向向量a,称向量a为平面????的法向量.
可以表示为集合{P∣????·????????=0}
?
如果另有一条直线m⊥????,在直线m上任取向量b , b与a有什么关系?
?
三.典例剖析
例1.已知长方体ABCD-?A1B1C1D1中,AB=4,BC=3,CC1 =2,M为AB中点.以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示空间直角坐标系,
(1)求平面BCC1B1的一个法向量.
(2)求平面MCA1的一个法向量.
x
y
z
D
A
B
C
D1
A1
B1
C1
M
(1)因为y轴垂直于平面BCC1B1,所以n1=(0,1,0)是平面BCC1B1的一个法向量.
解:
(2)因为AB=4, BC=3, CC1 =2,M是AB的中点,所以M,C,A的坐标分别为(3,2,0),(0,4,0),(3,0,2).因此
????????=(-3,2,0), ????????1=(0,-2,2),
设n2=(x,y,z)是平面MCA1的一个法向量,则
n2⊥ ????????,n2⊥????????1,
所以????2??????????=?3????+2????=0????2?????????1=?2????+2????=0 解得????=23????????=??
令z=3,则x=2,y=3,所以n2=(2,3,3)是平面MCA1的一个法向量.
?
归纳求解平面法向量的一般步骤:
(1)根据立体几何中线面垂直的判定定理得到法向量;
(2)根据向量运算的坐标表示得到两个三元一次方程,联立方程组;
(3)根据三元一次不定方程组,得到一个法向量.
设向量
选向量
列方程组
解方程组
赋非零值
得结论
练习
练习3.在长方体ABCD-?A1B1C1D1中,AB=4,BC=3,CC1 =2,以D为原点,以{13????????, 14????????, 12????????}为空间的一个单位正交基底,建立空间直角坐标系Oxyz,求平面ACD1的一个法向量.
?
x
y
z
D
A
B
C
D1
A1
B1
C1
1、判断下列命题是否正确
(1)零向量不能作为直线的方向向量和平面的法向量。 ( )
(2)若v是直线l的方向向量,则λv(λ∈R)也是直线l的方向向量。 ( )
(3)在空间直角坐标系中,j=(0,0,1)是坐标平面Oxy的一个法向量。 ( )
2、在平行六面体ABCD-A1B1C1D1中,????????=a , ????????=b , ????????1=c ,O是BD1与B1D的交点.
以{a,b,c}为空间的一个基底,求直线OA的一个方向向量.
?
练习
四.课堂小结
1、空间中点、直线和平面的向量表示
点→点+位置向量
线→点+方向向量
平面→点+法向量
设向量
选向量
列方程组
解方程组
赋非零值
得结论
2、归纳求平面法向量的步骤:
五.作业布置
课本P29 练习 3
课本P41 习题1.4 第1题
