思法数学 第3讲 子集
图片预览


文档简介
第3讲 子集、全集、补集
一【学习目标】
1.了解子集、真子集的定义,掌握集合之间的关系;
2.了解全集的意义;掌握补集的定义及其性质.
二【知识梳理】
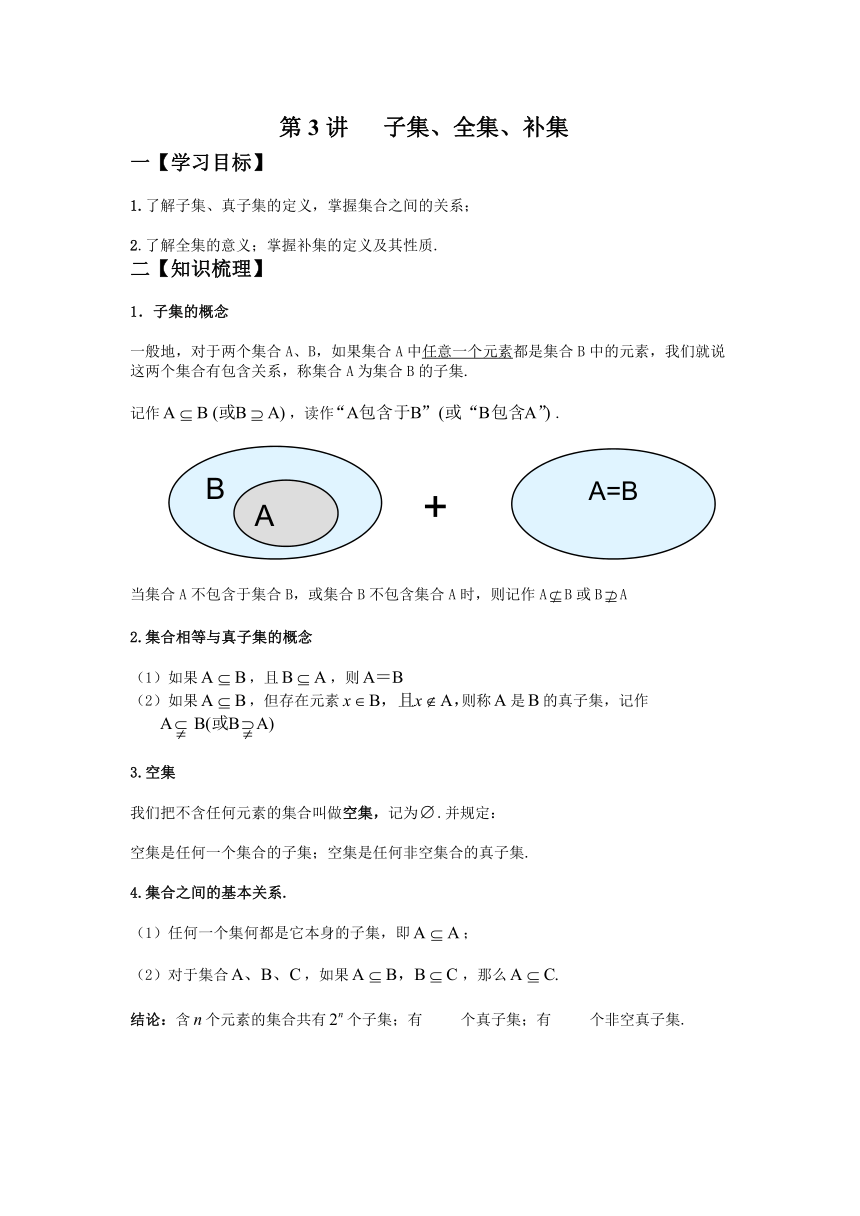
1.子集的概念
一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集.
记作,读作.
当集合A不包含于集合B,或集合B不包含集合A时,则记作AB或BA
2.集合相等与真子集的概念
(1)如果,且,则
(2)如果,但存在元素则称是的真子集,记作
3.空集
我们把不含任何元素的集合叫做空集,记为.并规定:
空集是任何一个集合的子集;空集是任何非空集合的真子集.
4.集合之间的基本关系.
(1)任何一个集何都是它本身的子集,即;
(2)对于集合,如果,那么
结论:含个元素的集合共有个子集;有 个真子集;有 个非空真子集.
5.补集:引入:观察下列三个集合:
U={高一年级的同学}——全集;
A={高一年级参加军训的同学};
B={高一年级没有参加军训的同学}.
(1),;
(2)集合B(或A)就是集合U中除去集合A(或B)之外.——补集
(3)Venn图表示
(1)定义
定义(1)所要研究的集合都是某个给定集合的子集,这个给定的集合就是全集.全集常用表示.
定义(2)设S是一个集合,A是S的一个子集(即),则由S中所有不属于A的元素组成的集合,叫做S中子集A的补集(或余集),记作,
(2)符号语言:
(3)图形语言:如右图:
(3)性质:;:.
三【典例精析】
例1.写出集合的所有子集和真子集.
解:集合的所有子集是:
,,,,,,,.
在上述子集中,除去集合A本身,即{1,2,3},剩下的都是A的真子集.
例2.说出下列每对集合之间的关系:
(1),;
(2),;
(3),.
解:(1);(2);(3).
例3.(1)填空:N___Z; N___Q; R___Z; R___Q; Φ___{0}.
(2)若A={x∈R|x-3x-4=0},B={x∈Z||x|<10},则AB正确吗?
(3)是否对任意一个集合A,都有AA,为什么?
(4)集合{a,b}的子集有那些?
(5)高一(1)班同学组成的集合A,高一年级同学组成的集合B,则A、B的关系为 .
解:(1);;;;.
(2)正确.
(3)是
(4),
(5)
点拨:
(1)“”与“”:元素与集合之间是属于关系;集合与集合之间是包含关系如ΦR,{1}{1,2,3}.
(2){0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合.
例4.填空:
(1)U={x|0≤X<6,X∈Z},A={1,3,5},B={1,4},
则=_____________,=_____________
(2)U={3,6,9},,则=________
(3)U={实数},A={有理数},则=________
(4)A={1,3,5},={2,4,6},B={4,6},则=________
(5)全集U={x|0则=___________________
例5.已知全集U=R,集合A={x|1≤2x+1<9},求.
例6.已知U={x|-1≤x+2<8},A={x|-2<1-x≤1},B={x|5<2x-1<11},讨论A与的关系
点拨:方法:数轴法和Venn图(图示法).
四【过关精练】
一、选择题
1.下列八个关系式①{0}=;②=0;③={};④{};⑤{0};⑥0;⑦{0};⑧{}其中正确的个数( )
A.4 B.5 C.6 D.7
2.集合{1,2,3}的真子集共有( )
A.5个 B.6个 C.7个 D.8个
3.集合A={x};B={};C={}
又则有( )
A.(a+b)A B.(a+b)B C.(a+b)C D.(a+b)A、B、C任一个
4.下列各组对象不能形成集合的是( )
A.大于6的所有整数 B.高中数学的所有难题
C.被3除余2的所有整数 D.函数y=1图象上所有的点
5.设集合=,则( )
A. B. C. D.
6.下列各式中,正确的是( )
A.2
B.{}
C.{}
D.{}={}
7.设一元二次方程的根的判别式,则不等式的解集为( )
A.R B. C.{} D.{}
8.集合A={x|x=2n+1,n∈Z}, B={y|y=4k±1,k∈Z},则A与B的关系为 ( )
A.AB B.AB C.A=B D.A≠B
二、填空题
9.在直角坐标系中,坐标轴上的点的集合可表示为__________________
10.设集合A={},B={x},且AB,则实数k的取值范围
是 。
11.若方程8x2+(k+1)x+k-7=0有两个负根,则k的取值范围是 .
12.集合{a,b,c}的所有子集是 ;
真子集是 ;
非空真子集是 .
13.方程x2-5x+6=0的解集可表示为 ;
方程组 .
三、解答题
14.已知方程x2-(k2-9)+k2-5k+6=0的一根小于1,另一根大于2,求实数k的取值范围。
15.设,,点(2,1)∈E,但(1,0)E,(3,2)E。求的值。
16.设全集U=﹛1,2,3,4,5﹜,A=﹛2,5﹜,求A的真子集的个数
17.已知全集={1,2,3,4},,求及.
18.设全集,,求实数的值.
参考答案
一、选择题
1.B;2。C;3。B;4。B;5。D;6。D;7。D;8。C
二、填空题
9.{(x,y) }
10.{}
11.{}
12.,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c};除去{a,b,c}外所有子集;除去及{a,b,c}外的所有子集
13.{2,3};{2,3}
三、解答题
14.解:令f(1)<0 且f(2)<0解得
15.解:∵点(2,1)∈E,∴(2-a)2+3b≤6 ①
∵点(1,0)E,∴(1-a)2+3b>0 ②
∵点(3,2)E,∴(3-a)2+3b>12 ③
由①②得6-(2-a)2>-(1-a)2,解得a>-;类似地由①③得a<-。
∴-B
A
+
A=B
U
A
S
A
一【学习目标】
1.了解子集、真子集的定义,掌握集合之间的关系;
2.了解全集的意义;掌握补集的定义及其性质.
二【知识梳理】
1.子集的概念
一般地,对于两个集合A、B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集.
记作,读作.
当集合A不包含于集合B,或集合B不包含集合A时,则记作AB或BA
2.集合相等与真子集的概念
(1)如果,且,则
(2)如果,但存在元素则称是的真子集,记作
3.空集
我们把不含任何元素的集合叫做空集,记为.并规定:
空集是任何一个集合的子集;空集是任何非空集合的真子集.
4.集合之间的基本关系.
(1)任何一个集何都是它本身的子集,即;
(2)对于集合,如果,那么
结论:含个元素的集合共有个子集;有 个真子集;有 个非空真子集.
5.补集:引入:观察下列三个集合:
U={高一年级的同学}——全集;
A={高一年级参加军训的同学};
B={高一年级没有参加军训的同学}.
(1),;
(2)集合B(或A)就是集合U中除去集合A(或B)之外.——补集
(3)Venn图表示
(1)定义
定义(1)所要研究的集合都是某个给定集合的子集,这个给定的集合就是全集.全集常用表示.
定义(2)设S是一个集合,A是S的一个子集(即),则由S中所有不属于A的元素组成的集合,叫做S中子集A的补集(或余集),记作,
(2)符号语言:
(3)图形语言:如右图:
(3)性质:;:.
三【典例精析】
例1.写出集合的所有子集和真子集.
解:集合的所有子集是:
,,,,,,,.
在上述子集中,除去集合A本身,即{1,2,3},剩下的都是A的真子集.
例2.说出下列每对集合之间的关系:
(1),;
(2),;
(3),.
解:(1);(2);(3).
例3.(1)填空:N___Z; N___Q; R___Z; R___Q; Φ___{0}.
(2)若A={x∈R|x-3x-4=0},B={x∈Z||x|<10},则AB正确吗?
(3)是否对任意一个集合A,都有AA,为什么?
(4)集合{a,b}的子集有那些?
(5)高一(1)班同学组成的集合A,高一年级同学组成的集合B,则A、B的关系为 .
解:(1);;;;.
(2)正确.
(3)是
(4),
(5)
点拨:
(1)“”与“”:元素与集合之间是属于关系;集合与集合之间是包含关系如ΦR,{1}{1,2,3}.
(2){0}与Φ:{0}是含有一个元素0的集合,Φ是不含任何元素的集合.
例4.填空:
(1)U={x|0≤X<6,X∈Z},A={1,3,5},B={1,4},
则=_____________,=_____________
(2)U={3,6,9},,则=________
(3)U={实数},A={有理数},则=________
(4)A={1,3,5},={2,4,6},B={4,6},则=________
(5)全集U={x|0
例5.已知全集U=R,集合A={x|1≤2x+1<9},求.
例6.已知U={x|-1≤x+2<8},A={x|-2<1-x≤1},B={x|5<2x-1<11},讨论A与的关系
点拨:方法:数轴法和Venn图(图示法).
四【过关精练】
一、选择题
1.下列八个关系式①{0}=;②=0;③={};④{};⑤{0};⑥0;⑦{0};⑧{}其中正确的个数( )
A.4 B.5 C.6 D.7
2.集合{1,2,3}的真子集共有( )
A.5个 B.6个 C.7个 D.8个
3.集合A={x};B={};C={}
又则有( )
A.(a+b)A B.(a+b)B C.(a+b)C D.(a+b)A、B、C任一个
4.下列各组对象不能形成集合的是( )
A.大于6的所有整数 B.高中数学的所有难题
C.被3除余2的所有整数 D.函数y=1图象上所有的点
5.设集合=,则( )
A. B. C. D.
6.下列各式中,正确的是( )
A.2
B.{}
C.{}
D.{}={}
7.设一元二次方程的根的判别式,则不等式的解集为( )
A.R B. C.{} D.{}
8.集合A={x|x=2n+1,n∈Z}, B={y|y=4k±1,k∈Z},则A与B的关系为 ( )
A.AB B.AB C.A=B D.A≠B
二、填空题
9.在直角坐标系中,坐标轴上的点的集合可表示为__________________
10.设集合A={},B={x},且AB,则实数k的取值范围
是 。
11.若方程8x2+(k+1)x+k-7=0有两个负根,则k的取值范围是 .
12.集合{a,b,c}的所有子集是 ;
真子集是 ;
非空真子集是 .
13.方程x2-5x+6=0的解集可表示为 ;
方程组 .
三、解答题
14.已知方程x2-(k2-9)+k2-5k+6=0的一根小于1,另一根大于2,求实数k的取值范围。
15.设,,点(2,1)∈E,但(1,0)E,(3,2)E。求的值。
16.设全集U=﹛1,2,3,4,5﹜,A=﹛2,5﹜,求A的真子集的个数
17.已知全集={1,2,3,4},,求及.
18.设全集,,求实数的值.
参考答案
一、选择题
1.B;2。C;3。B;4。B;5。D;6。D;7。D;8。C
二、填空题
9.{(x,y) }
10.{}
11.{}
12.,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c};除去{a,b,c}外所有子集;除去及{a,b,c}外的所有子集
13.{2,3};{2,3}
三、解答题
14.解:令f(1)<0 且f(2)<0解得
15.解:∵点(2,1)∈E,∴(2-a)2+3b≤6 ①
∵点(1,0)E,∴(1-a)2+3b>0 ②
∵点(3,2)E,∴(3-a)2+3b>12 ③
由①②得6-(2-a)2>-(1-a)2,解得a>-;类似地由①③得a<-。
∴-
A
+
A=B
U
A
S
A
