2020-2021学年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷(word版有答案)
文档属性
| 名称 | 2020-2021学年湘教新版七年级上册数学《第4章 图形的认识》单元测试卷(word版有答案) | 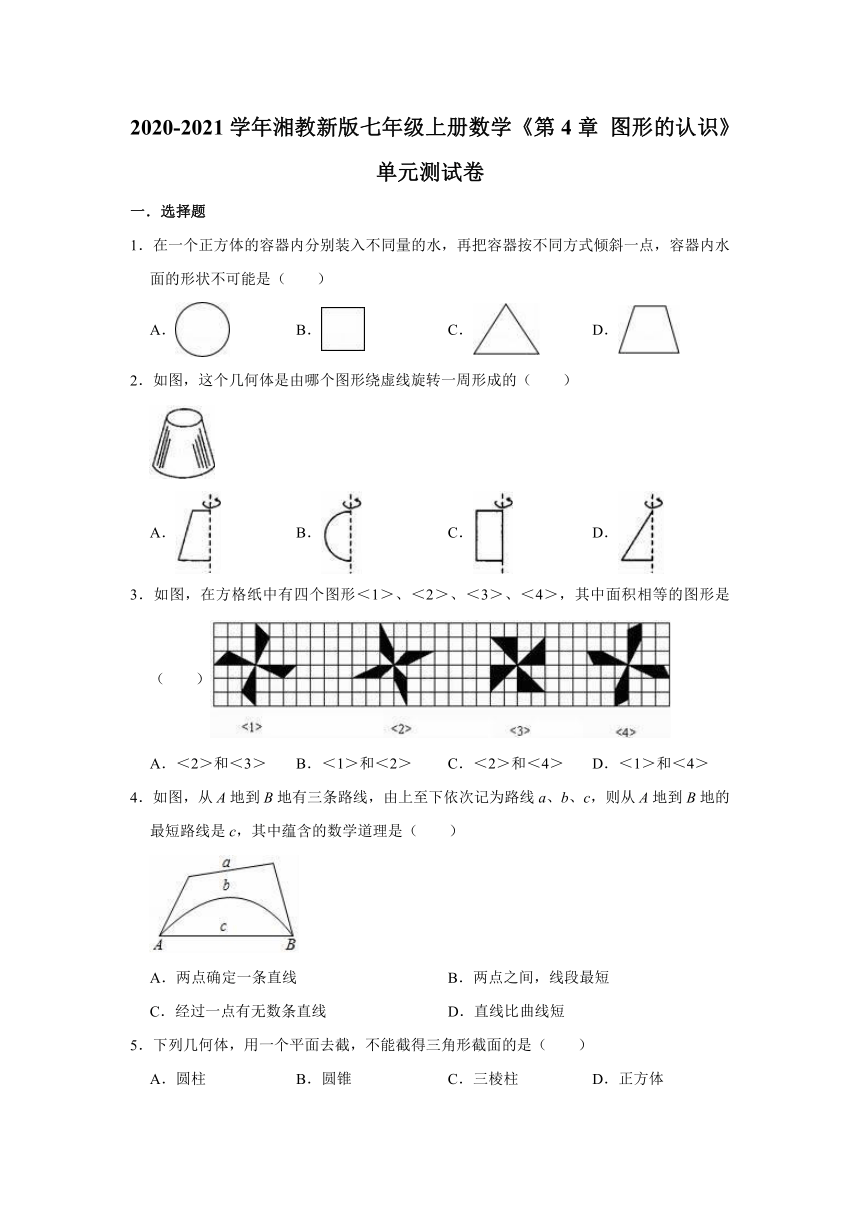 | |
| 格式 | zip | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 13:56:41 | ||
图片预览




文档简介
2020-2021学年湘教新版七年级上册数学《第4章
图形的认识》单元测试卷
一.选择题
1.在一个正方体的容器内分别装入不同量的水,再把容器按不同方式倾斜一点,容器内水面的形状不可能是( )
A.
B.
C.
D.
2.如图,这个几何体是由哪个图形绕虚线旋转一周形成的( )
A.
B.
C.
D.
3.如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是( )
A.<2>和<3>
B.<1>和<2>
C.<2>和<4>
D.<1>和<4>
4.如图,从A地到B地有三条路线,由上至下依次记为路线a、b、c,则从A地到B地的最短路线是c,其中蕴含的数学道理是( )
A.两点确定一条直线
B.两点之间,线段最短
C.经过一点有无数条直线
D.直线比曲线短
5.下列几何体,用一个平面去截,不能截得三角形截面的是( )
A.圆柱
B.圆锥
C.三棱柱
D.正方体
6.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
7.下列说法正确的是( )
A.延长射线AB到C
B.过三点能作且只能做一条直线
C.两点确定一条直线
D.若AC=BC,则C是线段AB的中点
8.如图,下列说法正确的是( )
A.射线AB
B.延长线段AB
C.反向延长线段BA
D.延长线段BA
9.下列说法不正确的有( )
①绝对值是本身的数是正数;
②符号不同的两个数互为相反数;
③两数相加,和一定大于任何一个加数;
④线段AB和线段BA表示的是同一条线段.
A.①③
B.②③
C.①②③
D.①②④
10.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.1cm
B.11cm
C.1cm
或11cm
D.2cm或11cm
二.填空题
11.如果一个棱柱共有15条棱,那么它一定是
棱柱.
12.如图,把甲乙两尺重叠在一起,如果甲尺是直的就可以判断乙尺是否是直的,其数学道理是
.
13.课本上有这样两个问题:如图,从甲地到乙地有3条路,走哪条路较近?从甲地到乙地能否修一条最短的路?这些问题均与关于线段的一个基本事实相关,这个基本事实是
.
14.若C、D是线段AB上两点,D是线段AC的中点,AB=10cm,BC=4cm,则AD的长是
cm.
15.直径为6cm的圆周长是
cm.
16.一个棱柱有6个面,则它的棱数是
.
17.以立方体的8个顶点中的任意3个顶点为顶点的三角形中,正三角形的个数为
.
18.往返于甲、乙两地的列车,中途需要停靠4个车站,如果每两站的路程都不相同,问:
(1)这两地之间有
种不同的票价;
(2)要准备
种不同的车票.
19.将如图所示的图形沿虚线旋转一周,所成的几何体是
.
20.如图,点A,B,C在直线l上,则图中共有
条线段,有
条射线.
三.解答题
21.如图,请度量出需要的数据,并计算阴影部分的面积.
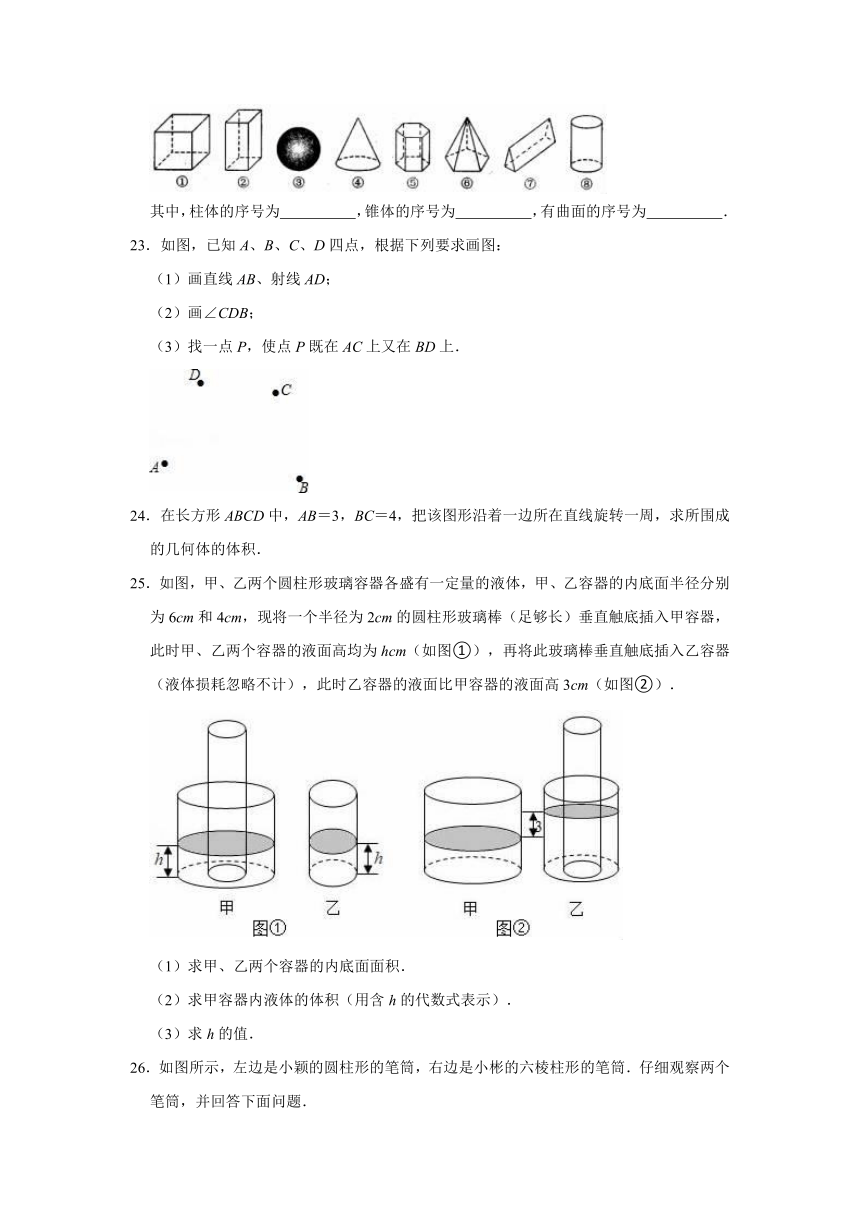
22.如图所示为8个立体图形.
其中,柱体的序号为
,锥体的序号为
,有曲面的序号为
.
23.如图,已知A、B、C、D四点,根据下列要求画图:
(1)画直线AB、射线AD;
(2)画∠CDB;
(3)找一点P,使点P既在AC上又在BD上.
24.在长方形ABCD中,AB=3,BC=4,把该图形沿着一边所在直线旋转一周,求所围成的几何体的体积.
25.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
26.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
27.如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有3条,如果线段AB上有4个点时,线段总数有6条,如果线段AB上有5个点时,线段总数共有10条,…
(1)当线段AB上有6个点时,线段总数共有
条;
(2)当线段AB上有n个点时,线段总数共有多少条?
参考答案与试题解析
一.选择题
1.解:根据题意,结合实际,容器内水面的形状不可能是椭圆.
故选:A.
2.解:根据以上分析及题目中的图形可知A旋转成圆台,B旋转成球体,C旋转成圆柱,D旋转成圆锥.
故选:A.
3.解:把图形中每一个方格的面积看作1,则图形(1)的面积是1.5×4=6,
图形(2)的面积是1.5×4=6,
图形(3)的面积是2×4=8,
图形(4)中一个图案的面积比1.5大且比2小,
所以(1)和(2)的面积相等.
故选:B.
4.解:从A地到B地的最短路线是c,其中蕴含的数学道理是两点之间线段最短,
故选:B.
5.解:用一个平面截一个几何体,不能截得三角形的截面的几何体有圆柱.
故选:A.
6.解:A、长方体是四棱柱,选项说法正确,不符合题意;
B、八棱柱有8+2=10个面,选项说法错误,符合题意;
C、六棱柱有2×6=12个顶点,选项说法正确,不符合题意;
D、经过棱柱的每个顶点有3条棱,选项说法正确,不符合题意;
故选:B.
7.解:A、射线本身是无限延伸的,不能延长,故本选项错误;
B、只有三点共线时才能做一条直线,故本选项错误;
C、两点确定一条直线,故本选项正确;
D、若AC=BC,此时点C在线段AB的垂直平分线上,故本选项错误;
故选:C.
8.解:A.图中的射线应该是射线BA,不是射线AB,故A不符合题意,
B.应该为延长线段BA,故B不符合题意,
C.反向延长线段BA是不符合图形的,故C不符合题意,
D.延长线段BA是符合图形的,故D符合题意,
故选:D.
9.解:①绝对值是本身的数是非负数,故①符合题意;
②符号不同的两个数不一定是互为相反数,故②符合题意;
③两数相加,和不一定大于任何一个加数,故③符合题意;
④线段AB和线段BA表示的是同一条线段,故④不符合题意,
故选:C.
10.解:如图,设较长的木条为AB=12cm,较短的木条为BC=10cm,
∵M、N分别为AB、BC的中点,
∴BM=6cm,BN=5cm,
①如图1,BC不在AB上时,MN=BM+BN=6+5=11cm,
②如图2,BC在AB上时,MN=BM﹣BN=6﹣5=1cm,
综上所述,两根木条的中点间的距离是1cm
或11cm,
故选:C.
二.填空题
11.解:15÷3=5,
所以是五棱柱,
故答案为:五.
12.解:∵甲尺是直的,两尺拼在一起两端重合,
∴甲乙两尺平行,
∴图中乙尺不可能是直的.
其数学道理是:两点确定一条直线.
故答案为:两点确定一条直线.
13.解:这个基本事实是:两点之间线段最短.
故答案为:两点之间线段最短.
14.解:如图:
∵AB=10cm,BC=4cm,
∴AC=AB﹣BC=6cm,
又点D是AC的中点,
∴AD=AC=3cm,
故答案为:3.
15.解:直径为6cm的圆周长是:6πcm.
故答案为:6π.
16.解:由n棱柱有(n+2)个面,
因此有n+2=6,
解得,n=4,
又四棱柱有4×3=12条棱,
故答案为:12.
17.解:如图所示:
正三角形的各边必为立方体各面的对角线,有△ADF,△ADH,△AFH,△BCE,△BCG,△BEG,△CEG,△DFH共8个正三角形.
故答案为:8.
18.解:(1)如图:
根据线段的定义:可知图中共有线段有AC,AD,AE,AF,AB,CD、CE,CF、CB、DE,DF、DB、EF,EB,FB共15条,有15种不同的票价;
(2)因车票需要考虑方向性,如,“A→C”与“C→A”票价相同,但车票不同,故需要准备30种车票.
故答案为:15;30.
19.解:由题意可知,该图是一个直角三角形,沿直角边旋转一周所成的几何体是圆锥.
故答案为圆锥.
20.解:图中有线段AB、AC、BC,共3条;
射线以A为端点的有2条,以B为端点的有2条,以C为端点的有2条,共6条.
故答案为:3;6.
三.解答题
21.解:测量可得半圆半径为2cm,扇形半径为4cm.
S半圆=3.14×22÷2=6.28(cm2),
S扇形=3.14×42÷4=12.56(cm2),
S阴影=12.56﹣6.28=6.28
(cm2).
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:(1)如图所示:直线AB、射线AD即为所求;
(2)如图所示:∠CDB即为所求;
(3)如图所示:点P即为所求.
24.解:分两种情况:
①当绕AB旋转时,则V=πBC2×AB=48π;
②当绕BC旋转时,则V=πAB2×BC=36π;
答:所围成的几何体的体积为48π或36π.
25.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
26.解:(1)圆柱有3个面,六棱柱有8个面,圆柱有两个平面,有一个曲面,棱柱的8个面都是平面;
(2)圆柱的侧面与底面相交形成1条线,是一条曲线;
(3)该棱柱共有12个顶点,经过每个顶点有3条棱;
(4)棱柱与圆柱的相同点是:都是柱体;
不同点是:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
27.解:(1)∵当有3个点时,线段的总数为:=3;
当有4个点时,线段的总数为:=6;
当有5个点时,线段的总数为:=10;
∴当有6个点时,线段的总数为:=15.
(2)由(1)可看出,当线段AB上有n个点时,线段总数为:.
图形的认识》单元测试卷
一.选择题
1.在一个正方体的容器内分别装入不同量的水,再把容器按不同方式倾斜一点,容器内水面的形状不可能是( )
A.
B.
C.
D.
2.如图,这个几何体是由哪个图形绕虚线旋转一周形成的( )
A.
B.
C.
D.
3.如图,在方格纸中有四个图形<1>、<2>、<3>、<4>,其中面积相等的图形是( )
A.<2>和<3>
B.<1>和<2>
C.<2>和<4>
D.<1>和<4>
4.如图,从A地到B地有三条路线,由上至下依次记为路线a、b、c,则从A地到B地的最短路线是c,其中蕴含的数学道理是( )
A.两点确定一条直线
B.两点之间,线段最短
C.经过一点有无数条直线
D.直线比曲线短
5.下列几何体,用一个平面去截,不能截得三角形截面的是( )
A.圆柱
B.圆锥
C.三棱柱
D.正方体
6.下列说法不正确的是( )
A.长方体是四棱柱
B.八棱柱有8个面
C.六棱柱有12个顶点
D.经过棱柱的每个顶点有3条棱
7.下列说法正确的是( )
A.延长射线AB到C
B.过三点能作且只能做一条直线
C.两点确定一条直线
D.若AC=BC,则C是线段AB的中点
8.如图,下列说法正确的是( )
A.射线AB
B.延长线段AB
C.反向延长线段BA
D.延长线段BA
9.下列说法不正确的有( )
①绝对值是本身的数是正数;
②符号不同的两个数互为相反数;
③两数相加,和一定大于任何一个加数;
④线段AB和线段BA表示的是同一条线段.
A.①③
B.②③
C.①②③
D.①②④
10.两根木条,一根长10cm,另一根长12cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A.1cm
B.11cm
C.1cm
或11cm
D.2cm或11cm
二.填空题
11.如果一个棱柱共有15条棱,那么它一定是
棱柱.
12.如图,把甲乙两尺重叠在一起,如果甲尺是直的就可以判断乙尺是否是直的,其数学道理是
.
13.课本上有这样两个问题:如图,从甲地到乙地有3条路,走哪条路较近?从甲地到乙地能否修一条最短的路?这些问题均与关于线段的一个基本事实相关,这个基本事实是
.
14.若C、D是线段AB上两点,D是线段AC的中点,AB=10cm,BC=4cm,则AD的长是
cm.
15.直径为6cm的圆周长是
cm.
16.一个棱柱有6个面,则它的棱数是
.
17.以立方体的8个顶点中的任意3个顶点为顶点的三角形中,正三角形的个数为
.
18.往返于甲、乙两地的列车,中途需要停靠4个车站,如果每两站的路程都不相同,问:
(1)这两地之间有
种不同的票价;
(2)要准备
种不同的车票.
19.将如图所示的图形沿虚线旋转一周,所成的几何体是
.
20.如图,点A,B,C在直线l上,则图中共有
条线段,有
条射线.
三.解答题
21.如图,请度量出需要的数据,并计算阴影部分的面积.
22.如图所示为8个立体图形.
其中,柱体的序号为
,锥体的序号为
,有曲面的序号为
.
23.如图,已知A、B、C、D四点,根据下列要求画图:
(1)画直线AB、射线AD;
(2)画∠CDB;
(3)找一点P,使点P既在AC上又在BD上.
24.在长方形ABCD中,AB=3,BC=4,把该图形沿着一边所在直线旋转一周,求所围成的几何体的体积.
25.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
26.如图所示,左边是小颖的圆柱形的笔筒,右边是小彬的六棱柱形的笔筒.仔细观察两个笔筒,并回答下面问题.
(1)圆柱、六棱柱各由几个面组成?它们都是平的吗?
(2)圆柱的侧面与底面相交成几条线?它们是直的吗?
(3)六棱柱有几个顶点?经过每个顶点有几条棱?
(4)试写出圆柱与棱柱的相同点与不同点.
27.如图,线段AB上的点数与线段的总数有如下关系:如果线段AB上有三个点时,线段总共有3条,如果线段AB上有4个点时,线段总数有6条,如果线段AB上有5个点时,线段总数共有10条,…
(1)当线段AB上有6个点时,线段总数共有
条;
(2)当线段AB上有n个点时,线段总数共有多少条?
参考答案与试题解析
一.选择题
1.解:根据题意,结合实际,容器内水面的形状不可能是椭圆.
故选:A.
2.解:根据以上分析及题目中的图形可知A旋转成圆台,B旋转成球体,C旋转成圆柱,D旋转成圆锥.
故选:A.
3.解:把图形中每一个方格的面积看作1,则图形(1)的面积是1.5×4=6,
图形(2)的面积是1.5×4=6,
图形(3)的面积是2×4=8,
图形(4)中一个图案的面积比1.5大且比2小,
所以(1)和(2)的面积相等.
故选:B.
4.解:从A地到B地的最短路线是c,其中蕴含的数学道理是两点之间线段最短,
故选:B.
5.解:用一个平面截一个几何体,不能截得三角形的截面的几何体有圆柱.
故选:A.
6.解:A、长方体是四棱柱,选项说法正确,不符合题意;
B、八棱柱有8+2=10个面,选项说法错误,符合题意;
C、六棱柱有2×6=12个顶点,选项说法正确,不符合题意;
D、经过棱柱的每个顶点有3条棱,选项说法正确,不符合题意;
故选:B.
7.解:A、射线本身是无限延伸的,不能延长,故本选项错误;
B、只有三点共线时才能做一条直线,故本选项错误;
C、两点确定一条直线,故本选项正确;
D、若AC=BC,此时点C在线段AB的垂直平分线上,故本选项错误;
故选:C.
8.解:A.图中的射线应该是射线BA,不是射线AB,故A不符合题意,
B.应该为延长线段BA,故B不符合题意,
C.反向延长线段BA是不符合图形的,故C不符合题意,
D.延长线段BA是符合图形的,故D符合题意,
故选:D.
9.解:①绝对值是本身的数是非负数,故①符合题意;
②符号不同的两个数不一定是互为相反数,故②符合题意;
③两数相加,和不一定大于任何一个加数,故③符合题意;
④线段AB和线段BA表示的是同一条线段,故④不符合题意,
故选:C.
10.解:如图,设较长的木条为AB=12cm,较短的木条为BC=10cm,
∵M、N分别为AB、BC的中点,
∴BM=6cm,BN=5cm,
①如图1,BC不在AB上时,MN=BM+BN=6+5=11cm,
②如图2,BC在AB上时,MN=BM﹣BN=6﹣5=1cm,
综上所述,两根木条的中点间的距离是1cm
或11cm,
故选:C.
二.填空题
11.解:15÷3=5,
所以是五棱柱,
故答案为:五.
12.解:∵甲尺是直的,两尺拼在一起两端重合,
∴甲乙两尺平行,
∴图中乙尺不可能是直的.
其数学道理是:两点确定一条直线.
故答案为:两点确定一条直线.
13.解:这个基本事实是:两点之间线段最短.
故答案为:两点之间线段最短.
14.解:如图:
∵AB=10cm,BC=4cm,
∴AC=AB﹣BC=6cm,
又点D是AC的中点,
∴AD=AC=3cm,
故答案为:3.
15.解:直径为6cm的圆周长是:6πcm.
故答案为:6π.
16.解:由n棱柱有(n+2)个面,
因此有n+2=6,
解得,n=4,
又四棱柱有4×3=12条棱,
故答案为:12.
17.解:如图所示:
正三角形的各边必为立方体各面的对角线,有△ADF,△ADH,△AFH,△BCE,△BCG,△BEG,△CEG,△DFH共8个正三角形.
故答案为:8.
18.解:(1)如图:
根据线段的定义:可知图中共有线段有AC,AD,AE,AF,AB,CD、CE,CF、CB、DE,DF、DB、EF,EB,FB共15条,有15种不同的票价;
(2)因车票需要考虑方向性,如,“A→C”与“C→A”票价相同,但车票不同,故需要准备30种车票.
故答案为:15;30.
19.解:由题意可知,该图是一个直角三角形,沿直角边旋转一周所成的几何体是圆锥.
故答案为圆锥.
20.解:图中有线段AB、AC、BC,共3条;
射线以A为端点的有2条,以B为端点的有2条,以C为端点的有2条,共6条.
故答案为:3;6.
三.解答题
21.解:测量可得半圆半径为2cm,扇形半径为4cm.
S半圆=3.14×22÷2=6.28(cm2),
S扇形=3.14×42÷4=12.56(cm2),
S阴影=12.56﹣6.28=6.28
(cm2).
22.解:柱体的序号为①②⑤⑦⑧,锥体的序号为④⑥,有曲面的序号为③④⑧,
故答案为:①②⑤⑦⑧;④⑥;③④⑧.
23.解:(1)如图所示:直线AB、射线AD即为所求;
(2)如图所示:∠CDB即为所求;
(3)如图所示:点P即为所求.
24.解:分两种情况:
①当绕AB旋转时,则V=πBC2×AB=48π;
②当绕BC旋转时,则V=πAB2×BC=36π;
答:所围成的几何体的体积为48π或36π.
25.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm3).
答:甲容器内液体的体积为32πh(cm3).
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
26.解:(1)圆柱有3个面,六棱柱有8个面,圆柱有两个平面,有一个曲面,棱柱的8个面都是平面;
(2)圆柱的侧面与底面相交形成1条线,是一条曲线;
(3)该棱柱共有12个顶点,经过每个顶点有3条棱;
(4)棱柱与圆柱的相同点是:都是柱体;
不同点是:棱柱与圆柱的底面形状不同,棱柱的底面是多边形,圆柱的底面是圆形,圆柱的侧面是曲面,而棱柱的侧面是长方形.
27.解:(1)∵当有3个点时,线段的总数为:=3;
当有4个点时,线段的总数为:=6;
当有5个点时,线段的总数为:=10;
∴当有6个点时,线段的总数为:=15.
(2)由(1)可看出,当线段AB上有n个点时,线段总数为:.
同课章节目录
