2020-2021学年苏科新版八年级上册数学《第5章 平面直角坐标系》单元测试卷(word版有答案)
文档属性
| 名称 | 2020-2021学年苏科新版八年级上册数学《第5章 平面直角坐标系》单元测试卷(word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 167.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 09:47:02 | ||
图片预览




文档简介
2020-2021学年苏科新版八年级上册数学《第5章
平面直角坐标系》单元测试卷
一.选择题
1.点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴的坐标是( )
A.(8,0)
B.(0,﹣8)
C.(0,8)
D.(﹣8,0)
2.已知点A的坐标为(﹣2,3),则点A关于y轴的对称点的坐标是( )
A.(﹣2,3)
B.(2,3)
C.(2,﹣3)
D.(﹣2,﹣3)
3.根据下列表述,不能确定具体位置的是( )
A.教室内的3排4列
B.渠江镇胜利街道15号
C.南偏西30°
D.东经108°,北纬53°
4.在平面直角坐标系中,点P在第四象限,距离x轴4个单位长度,距离y轴3个单位长度,则点P的坐标是( )
A.(4,﹣3)
B.(﹣4,3)
C.(3,﹣4)
D.(﹣3,4)
5.P1(x1,y1),P2(x2,y2)是平面直角坐标系中的任意两点,我们把|x1﹣x2|+|y1﹣y2|叫做P1,P2两点间的“直角距离”,记作d(P1,P2).已知动点P(x,y),定点Q(2,1)满足d(P,Q)=2,且x、y均为整数,则满足条件的点P有( )个
A.4
B.6
C.8
D.10
6.如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点M(﹣1,1)和点N(﹣1,﹣3),则第一架轰炸机位于的点P的坐标是( )
A.(﹣1,﹣3)
B.(3,﹣1)
C.(﹣1,3)
D.(3,0)
7.点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,则点P的坐标为( )
A.(3,3)
B.(3,﹣3)
C.(6,﹣6)
D.(3,3)或(6,﹣6)
8.点(2,﹣2)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
9.平面直角坐标系中,已知点P(a,﹣3)在第四象限,则点P关于直线x=2对称的点的坐标是( )
A.(a,1)
B.(﹣a+2,﹣3)
C.(﹣a+4,﹣3)
D.(﹣a,﹣3)
10.在平面直角坐标系中,将点P(m﹣1,n+2)向右平移3个单位,再向上平移2个单位,得到点Q.若点Q位于第二象限,则m,n的取值范围是( )
A.m<0,n>0
B.m<0,n<﹣2
C.m<﹣2,n>﹣4
D.m<1,n>﹣2
二.填空题
11.若点P(m+3,m+1)在x轴上,则点P的坐标为
.
12.如图,将正整数按有图所示规律排列下去,若用有序数对(n,m)表示n排从左到右第m个数.如(4,3)表示9,则(10,3)表示
.
13.将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是
.
14.如图,线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为
.
15.若点P(m﹣2,m+1)在y轴上,则点P的坐标为
.
16.若P(a+2,a﹣1)在y轴上,则点P的坐标是
.
17.已知点A(4,y),B(x,﹣3),若AB∥x轴,且线段AB的长为5,x=
,y=
.
18.点P(2,﹣5)关于x轴对称的点的坐标为
.
19.在平面直角坐标系中点A(,1)到原点的距离是
.
20.如图,在平面直角坐标系中,一颗棋子从点P(0,﹣2)处开始依次关于点A(﹣1,﹣1),B(1,2),C(2,1)作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2011次跳动之后,棋子落点的坐标为
.
三.解答题
21.已知平面直角坐标系中,点P的坐标为(m﹣1,2m+3)
(1)当m为何值时,点P到x轴的距离为1?
(2)当m为何值时,点P到y轴的距离为2?
(3)点P可能在第一象限坐标轴夹角的平分线上吗?若可能,求出m的值;若不可能,请说明理由.
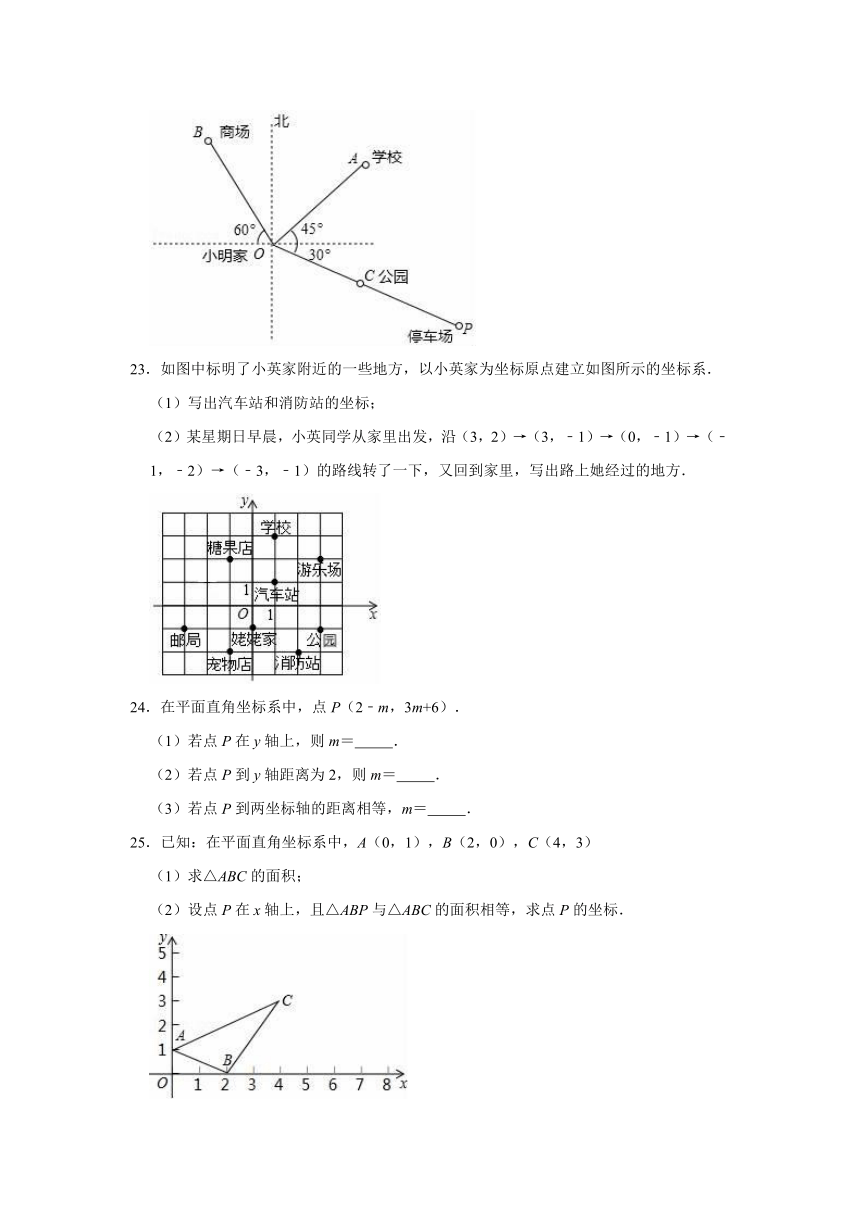
22.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的地方是哪个?
(2)请用方向与距离描述学校、商场、停车场相对于小明家的位置.
23.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2)→(3,﹣1)→(0,﹣1)→(﹣1,﹣2)→(﹣3,﹣1)的路线转了一下,又回到家里,写出路上她经过的地方.
24.在平面直角坐标系中,点P(2﹣m,3m+6).
(1)若点P在y轴上,则m=
.
(2)若点P到y轴距离为2,则m=
.
(3)若点P到两坐标轴的距离相等,m=
.
25.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.
26.先阅读下列一段文字,在回答后面的问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.
(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
27.已知平面直角坐标中有一点M(2﹣a,3a+6),点M到两坐标轴的距离相等,求M的坐标.
参考答案与试题解析
一.选择题
1.解:∵点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴,
∴A为圆心,5为半径画圆交y轴负半轴的长度是:3+5=8,
故坐标为:(0,﹣8),
故选:B.
2.解:∵点A的坐标为(﹣2,3),
∴点A关于y轴的对称点的坐标是(2,3),
故选:B.
3.解:A、教室内的3排4列,可以确定具体位置,不合题意;
B、渠江镇胜利街道15号,可以确定具体位置,不合题意;
C、南偏西30°,不能确定具体位置,符合题意;
D、东经108°,北纬53°,可以确定具体位置,不合题意;
故选:C.
4.解:∵点P位于第四象限,且距离x轴4个单位长度,距离y轴3个单位长度,
∴点P的纵坐标为﹣4,横坐标为3,即点P的坐标为(3,﹣4),
故选:C.
5.解:依题意有,
|x﹣2|+|y﹣1|=2,
①x﹣2=±2,y﹣1=0,
解得,;
②x﹣2=±1,y﹣1=±1,
解得,,,;
③x﹣2=0,y﹣1=±2,
解得,.
故满足条件的点P有8个.
故选:C.
6.解:因为M(﹣1,1)和点N(﹣1,﹣3),所以可建立如下图所示平面直角坐标系:
所以可得点P的坐标为(3,﹣1),
故选:B.
7.解:∵点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,
∴|2﹣a|=|3a+6|,
∴2﹣a=±(3a+6)
解得a=﹣1或a=﹣4,
即点P的坐标为(3,3)或(6,﹣6).
故选:D.
8.解:由题可得,点(2,﹣2)所在的象限是第四象限,
故选:D.
9.解:设P(a,﹣3)关于直线x=2的对称点为P′(m,﹣3),
则有=2,
∴m=4﹣a,
∴P′(﹣a+4,﹣3),
故选:C.
10.解:点A(m﹣1,n+2)先向右平移3个单位,再向上平移2个单位得到点A′(m+2,n+4),
∵点A′位于第二象限,
∴,
解得:m<﹣2,n>﹣4,
故选:C.
二.填空题
11.解:∵点P(m+3,m+1)在x轴上,
∴m+1=0,
解得m=﹣1,
∴m+3=﹣1+3=2,
∴点P的坐标为(2,0).
故答案为:(2,0).
12.解:∵(4,3)表示第4排从左数第3个数,即为9,
∴依题意得(10,3)表示第10排从左数第3个数,第9排最后一个数为45,则第10排从左数第3个数即为48.
故答案填:48.
13.解:将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是(1+2,2)
即(3,2),
故答案为:(3,2).
14.解:∵线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),
∴∠AOB=90°,∠AOC=45°,
则C点可表示为(2,75°).
故答案为:(2,75°).
15.解:∵点P(m﹣2,m+1)在y轴上,
∴m﹣2=0,
解得m=2,
所以m+1=2+1=3,
所以点P的坐标为(0,3).
故答案为:(0,3).
16.解:∵P(a+2,a﹣1)在y轴上,
∴a+2=0,
解得a=﹣2,
∴点P的坐标是
(0,﹣3),
故答案为(0,﹣3).
17.解:若AB∥x轴,则A,B的纵坐标相同,因而y=﹣3;
线段AB的长为5,即|x﹣4|=5,解得x=9或﹣1.
故答案填:9或﹣1,﹣3.
18.解:点P(2,﹣5)关于x轴对称的点的坐标为:(2,5),
故答案为:(2,5).
19.解:点A(,1)到原点的距离是=2.
故答案为:2.
20.解:∵棋子跳动3次后又回点P处,
∴经过第2011次跳动后,即2011÷3=670余1,棋子落在点M处,
其坐标为M(﹣2,0);
故答案为(﹣2,0).
三.解答题
21.解:(1)∵点P到x轴的距离为1
∴|2m+3|=1
∴m1=﹣1,m2=﹣2
(2)∵点P到y轴的距离为2
∴|m﹣1|=2
∴m1=3,m2=﹣1
(3)∵点P可能在第一象限坐标轴夹角的平分线上
∴m﹣1=2m+3
∴m=﹣4
∵点P在第一象限
∴m﹣1>0,2m+3>0
∴m>1
∴m=﹣4不合题意
∴点P不可能在第一象限坐标轴夹角的平分线上.
22.解:(1)∵点C为OP的中点,
∴OC=OP=×4=2km,
∵OA=2km,
∴距小明家距离相同的是学校和公园.
(2)学校在小明家北偏东45°的方向上,且到小明家的距离为2km,
商场在小明家北偏西30°的方向上,且到小明家的距离为3.5km,
停车场在小明家南偏东60°的方向上,且到小明家的距离为4km.
23.解:(1)汽车站(1,1),消防站(2,﹣2);
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
24.解:(1)根据题意得2﹣m=0,解得m=2;
(2)根据题意得|2﹣m|=2,解得m=0或4;
(3)2﹣m=3m+6或2﹣m=﹣(3m+6),
所以m=﹣1或﹣4.
故答案为2;0或4;﹣1或﹣4.
25.解:(1)过点C作CD⊥x轴,CE⊥y,垂足分别为D、E.
S△ABC=S四边形CDEO﹣S△AEC﹣S△ABO﹣S△BCD
=3×4﹣×2×4﹣×1×2﹣×2×3
=12﹣4﹣1﹣3
=4.
(2)设点P的坐标为(x,0),则BP=|x﹣2|.
∵△ABP与△ABC的面积相等,
∴×1×|x﹣2|=4.
解得:x=10或x=﹣6.
所以点P的坐标为(10,0)或(﹣6,0).
26.解:(1)∵A(2,4)、B(﹣3,﹣8),
∴|AB|==13,即A、B两点间的距离是13;
(2)∵A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,
∴|AB|=|﹣1﹣5|=6,即A、B两点间的距离是6;
(3)△ABC是等腰三角形,理由如下:
∵一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),
∴AB=5,BC=6,AC=5,
∴AB=AC,
∴△ABC是等腰三角形.
27.解:∵点M的坐标为(2﹣a,3a+6),且点M到两坐标轴的距离相等,
∴2﹣a=3a+6或(2﹣a)+(3a+6)=0,
解得,a=﹣1或a=﹣4,
∴M点坐标为(3,3)或(6,﹣6).
平面直角坐标系》单元测试卷
一.选择题
1.点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴的坐标是( )
A.(8,0)
B.(0,﹣8)
C.(0,8)
D.(﹣8,0)
2.已知点A的坐标为(﹣2,3),则点A关于y轴的对称点的坐标是( )
A.(﹣2,3)
B.(2,3)
C.(2,﹣3)
D.(﹣2,﹣3)
3.根据下列表述,不能确定具体位置的是( )
A.教室内的3排4列
B.渠江镇胜利街道15号
C.南偏西30°
D.东经108°,北纬53°
4.在平面直角坐标系中,点P在第四象限,距离x轴4个单位长度,距离y轴3个单位长度,则点P的坐标是( )
A.(4,﹣3)
B.(﹣4,3)
C.(3,﹣4)
D.(﹣3,4)
5.P1(x1,y1),P2(x2,y2)是平面直角坐标系中的任意两点,我们把|x1﹣x2|+|y1﹣y2|叫做P1,P2两点间的“直角距离”,记作d(P1,P2).已知动点P(x,y),定点Q(2,1)满足d(P,Q)=2,且x、y均为整数,则满足条件的点P有( )个
A.4
B.6
C.8
D.10
6.如图是一轰炸机群的飞行队形示意图,若在图上建立平面直角坐标,使最后两架轰炸机分别位于点M(﹣1,1)和点N(﹣1,﹣3),则第一架轰炸机位于的点P的坐标是( )
A.(﹣1,﹣3)
B.(3,﹣1)
C.(﹣1,3)
D.(3,0)
7.点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,则点P的坐标为( )
A.(3,3)
B.(3,﹣3)
C.(6,﹣6)
D.(3,3)或(6,﹣6)
8.点(2,﹣2)所在的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
9.平面直角坐标系中,已知点P(a,﹣3)在第四象限,则点P关于直线x=2对称的点的坐标是( )
A.(a,1)
B.(﹣a+2,﹣3)
C.(﹣a+4,﹣3)
D.(﹣a,﹣3)
10.在平面直角坐标系中,将点P(m﹣1,n+2)向右平移3个单位,再向上平移2个单位,得到点Q.若点Q位于第二象限,则m,n的取值范围是( )
A.m<0,n>0
B.m<0,n<﹣2
C.m<﹣2,n>﹣4
D.m<1,n>﹣2
二.填空题
11.若点P(m+3,m+1)在x轴上,则点P的坐标为
.
12.如图,将正整数按有图所示规律排列下去,若用有序数对(n,m)表示n排从左到右第m个数.如(4,3)表示9,则(10,3)表示
.
13.将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是
.
14.如图,线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),则C点可表示为
.
15.若点P(m﹣2,m+1)在y轴上,则点P的坐标为
.
16.若P(a+2,a﹣1)在y轴上,则点P的坐标是
.
17.已知点A(4,y),B(x,﹣3),若AB∥x轴,且线段AB的长为5,x=
,y=
.
18.点P(2,﹣5)关于x轴对称的点的坐标为
.
19.在平面直角坐标系中点A(,1)到原点的距离是
.
20.如图,在平面直角坐标系中,一颗棋子从点P(0,﹣2)处开始依次关于点A(﹣1,﹣1),B(1,2),C(2,1)作循环对称跳动,即第一次跳到点P关于点A的对称点M处,接着跳到点M关于点B的对称点N处,第三次再跳到点N关于点C的对称点处,…,如此下去.则经过第2011次跳动之后,棋子落点的坐标为
.
三.解答题
21.已知平面直角坐标系中,点P的坐标为(m﹣1,2m+3)
(1)当m为何值时,点P到x轴的距离为1?
(2)当m为何值时,点P到y轴的距离为2?
(3)点P可能在第一象限坐标轴夹角的平分线上吗?若可能,求出m的值;若不可能,请说明理由.
22.如图,是小明家和学校所在地的简单地图,已知OA=2km,OB=3.5km,OP=4km,点C为OP的中点,回答下列问题:
(1)图中距小明家距离相同的地方是哪个?
(2)请用方向与距离描述学校、商场、停车场相对于小明家的位置.
23.如图中标明了小英家附近的一些地方,以小英家为坐标原点建立如图所示的坐标系.
(1)写出汽车站和消防站的坐标;
(2)某星期日早晨,小英同学从家里出发,沿(3,2)→(3,﹣1)→(0,﹣1)→(﹣1,﹣2)→(﹣3,﹣1)的路线转了一下,又回到家里,写出路上她经过的地方.
24.在平面直角坐标系中,点P(2﹣m,3m+6).
(1)若点P在y轴上,则m=
.
(2)若点P到y轴距离为2,则m=
.
(3)若点P到两坐标轴的距离相等,m=
.
25.已知:在平面直角坐标系中,A(0,1),B(2,0),C(4,3)
(1)求△ABC的面积;
(2)设点P在x轴上,且△ABP与△ABC的面积相等,求点P的坐标.
26.先阅读下列一段文字,在回答后面的问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离公式,同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,试求A、B两点间的距离.
(3)已知一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),你能判定此三角形的形状吗?说明理由.
27.已知平面直角坐标中有一点M(2﹣a,3a+6),点M到两坐标轴的距离相等,求M的坐标.
参考答案与试题解析
一.选择题
1.解:∵点A(0,﹣3),以A为圆心,5为半径画圆交y轴负半轴,
∴A为圆心,5为半径画圆交y轴负半轴的长度是:3+5=8,
故坐标为:(0,﹣8),
故选:B.
2.解:∵点A的坐标为(﹣2,3),
∴点A关于y轴的对称点的坐标是(2,3),
故选:B.
3.解:A、教室内的3排4列,可以确定具体位置,不合题意;
B、渠江镇胜利街道15号,可以确定具体位置,不合题意;
C、南偏西30°,不能确定具体位置,符合题意;
D、东经108°,北纬53°,可以确定具体位置,不合题意;
故选:C.
4.解:∵点P位于第四象限,且距离x轴4个单位长度,距离y轴3个单位长度,
∴点P的纵坐标为﹣4,横坐标为3,即点P的坐标为(3,﹣4),
故选:C.
5.解:依题意有,
|x﹣2|+|y﹣1|=2,
①x﹣2=±2,y﹣1=0,
解得,;
②x﹣2=±1,y﹣1=±1,
解得,,,;
③x﹣2=0,y﹣1=±2,
解得,.
故满足条件的点P有8个.
故选:C.
6.解:因为M(﹣1,1)和点N(﹣1,﹣3),所以可建立如下图所示平面直角坐标系:
所以可得点P的坐标为(3,﹣1),
故选:B.
7.解:∵点P的坐标为(2﹣a,3a+6),且到两坐标轴的距离相等,
∴|2﹣a|=|3a+6|,
∴2﹣a=±(3a+6)
解得a=﹣1或a=﹣4,
即点P的坐标为(3,3)或(6,﹣6).
故选:D.
8.解:由题可得,点(2,﹣2)所在的象限是第四象限,
故选:D.
9.解:设P(a,﹣3)关于直线x=2的对称点为P′(m,﹣3),
则有=2,
∴m=4﹣a,
∴P′(﹣a+4,﹣3),
故选:C.
10.解:点A(m﹣1,n+2)先向右平移3个单位,再向上平移2个单位得到点A′(m+2,n+4),
∵点A′位于第二象限,
∴,
解得:m<﹣2,n>﹣4,
故选:C.
二.填空题
11.解:∵点P(m+3,m+1)在x轴上,
∴m+1=0,
解得m=﹣1,
∴m+3=﹣1+3=2,
∴点P的坐标为(2,0).
故答案为:(2,0).
12.解:∵(4,3)表示第4排从左数第3个数,即为9,
∴依题意得(10,3)表示第10排从左数第3个数,第9排最后一个数为45,则第10排从左数第3个数即为48.
故答案填:48.
13.解:将一点A(1,2)向右平移2个单位得到一个对应点A′,则点A′的坐标是(1+2,2)
即(3,2),
故答案为:(3,2).
14.解:∵线段OB、OC、OA的长度分别是1、2、3,且OC平分∠AOB.若将A点表示为(3,30°),B点表示为(1,120°),
∴∠AOB=90°,∠AOC=45°,
则C点可表示为(2,75°).
故答案为:(2,75°).
15.解:∵点P(m﹣2,m+1)在y轴上,
∴m﹣2=0,
解得m=2,
所以m+1=2+1=3,
所以点P的坐标为(0,3).
故答案为:(0,3).
16.解:∵P(a+2,a﹣1)在y轴上,
∴a+2=0,
解得a=﹣2,
∴点P的坐标是
(0,﹣3),
故答案为(0,﹣3).
17.解:若AB∥x轴,则A,B的纵坐标相同,因而y=﹣3;
线段AB的长为5,即|x﹣4|=5,解得x=9或﹣1.
故答案填:9或﹣1,﹣3.
18.解:点P(2,﹣5)关于x轴对称的点的坐标为:(2,5),
故答案为:(2,5).
19.解:点A(,1)到原点的距离是=2.
故答案为:2.
20.解:∵棋子跳动3次后又回点P处,
∴经过第2011次跳动后,即2011÷3=670余1,棋子落在点M处,
其坐标为M(﹣2,0);
故答案为(﹣2,0).
三.解答题
21.解:(1)∵点P到x轴的距离为1
∴|2m+3|=1
∴m1=﹣1,m2=﹣2
(2)∵点P到y轴的距离为2
∴|m﹣1|=2
∴m1=3,m2=﹣1
(3)∵点P可能在第一象限坐标轴夹角的平分线上
∴m﹣1=2m+3
∴m=﹣4
∵点P在第一象限
∴m﹣1>0,2m+3>0
∴m>1
∴m=﹣4不合题意
∴点P不可能在第一象限坐标轴夹角的平分线上.
22.解:(1)∵点C为OP的中点,
∴OC=OP=×4=2km,
∵OA=2km,
∴距小明家距离相同的是学校和公园.
(2)学校在小明家北偏东45°的方向上,且到小明家的距离为2km,
商场在小明家北偏西30°的方向上,且到小明家的距离为3.5km,
停车场在小明家南偏东60°的方向上,且到小明家的距离为4km.
23.解:(1)汽车站(1,1),消防站(2,﹣2);
(2)小英经过的地方:游乐场,公园,姥姥家,宠物店,邮局.
24.解:(1)根据题意得2﹣m=0,解得m=2;
(2)根据题意得|2﹣m|=2,解得m=0或4;
(3)2﹣m=3m+6或2﹣m=﹣(3m+6),
所以m=﹣1或﹣4.
故答案为2;0或4;﹣1或﹣4.
25.解:(1)过点C作CD⊥x轴,CE⊥y,垂足分别为D、E.
S△ABC=S四边形CDEO﹣S△AEC﹣S△ABO﹣S△BCD
=3×4﹣×2×4﹣×1×2﹣×2×3
=12﹣4﹣1﹣3
=4.
(2)设点P的坐标为(x,0),则BP=|x﹣2|.
∵△ABP与△ABC的面积相等,
∴×1×|x﹣2|=4.
解得:x=10或x=﹣6.
所以点P的坐标为(10,0)或(﹣6,0).
26.解:(1)∵A(2,4)、B(﹣3,﹣8),
∴|AB|==13,即A、B两点间的距离是13;
(2)∵A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为﹣1,
∴|AB|=|﹣1﹣5|=6,即A、B两点间的距离是6;
(3)△ABC是等腰三角形,理由如下:
∵一个三角形各顶点坐标为A(0,6)、B(﹣3,2)、C(3,2),
∴AB=5,BC=6,AC=5,
∴AB=AC,
∴△ABC是等腰三角形.
27.解:∵点M的坐标为(2﹣a,3a+6),且点M到两坐标轴的距离相等,
∴2﹣a=3a+6或(2﹣a)+(3a+6)=0,
解得,a=﹣1或a=﹣4,
∴M点坐标为(3,3)或(6,﹣6).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
