2021-2022学年人教版九年级上册数学 21.2.4一元二次方程的根与系数的关系课件(15张PPT)
文档属性
| 名称 | 2021-2022学年人教版九年级上册数学 21.2.4一元二次方程的根与系数的关系课件(15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 16:31:48 | ||
图片预览






文档简介
(共15张PPT)
一元二次方程
的根与系数的关系
复习旧知
1、一元二次方程的一般形式是什么?并指出它的二次
项系数、一次项系数、常数项.
二次项系数:
一次项系数:
常数项:
2、一元二次方程解法中的公式法,它的求根公
式是什么?
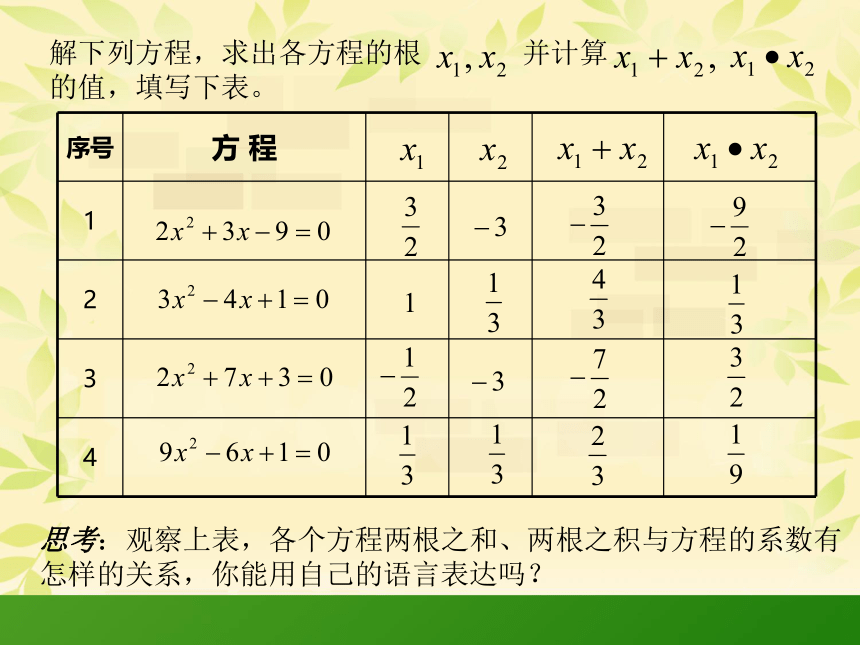
思考:观察上表,各个方程两根之和、两根之积与方程的系数有
怎样的关系,你能用自己的语言表达吗?
解下列方程,求出各方程的根
并计算
的值,填写下表。
序号
方
程
1
2
3
4
猜想:
1、不解方程,
的两根为
则
则
a
b
-
=
=
=
a
b
-
2
2
a
ac
b
b
ac
b
b
-
-
-
-
+
-
2
4
4
2
2
a
c
=
=
=
·
=
x
x
·
2
1
a
ac
2
4
4
a
ac
b
b
-
-
-
2
2
4
a
ac
b
b
-
+
-
2
2
4
小练习
1、下列各方程中,两根之和与两根之积各是多少?
3、已知一个长方形的长和宽是方程
的两个根,那么这个长方形的周长是
,面积是
.
(2)
(1)
(4)
(5)
(3)
2、请指出下列方程后面括号内的两个数是不是它的两个根。
(1)
(2)
9
解:
解得:
例2
当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2=
,
x1x2=
∴
解得k1=9,k2=
-3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
小练习
.
.
,
,
16
13
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。
解:设方程的另一个根为x1,
则x1+1=
,
∴
x1=
,
又x1●1=
,
∴
m=
3x1
=
16
解:
由根与系数的关系,得
x1+x2=
-
2
,
x1
·
x2=
∴
(x1+1)(x2+1)
=
x1
x2
+
(x1+x2)+1
=-2+(
)+1=
2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
拓广探索
解:由方程有两个实数根,得
即-8k+4≥0
由根与系数的关系得x1+x2=
2(k-1)
,
x1x2=k2
∴
X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4
由X12+x22
=4,得2k2-8k+4=4
解得k1=0
,
k2=4
经检验,
k2=4不合题意,舍去。
∴
k=0
回顾小结
一种方法:
一个定理:
观察、分析、猜测、验证
(从特殊到一般)
韦达定理
布置作业
1、课堂作业:习题第3、4题。
2、思考题:设x1,x2是方程2x2+4x-3=0的两个根,利用根与系数的关系求下列代数式的值:
(1)(x1+1)(x2+1)
(2)x12+x22
感谢各位专家
莅临指导!
一元二次方程
的根与系数的关系
复习旧知
1、一元二次方程的一般形式是什么?并指出它的二次
项系数、一次项系数、常数项.
二次项系数:
一次项系数:
常数项:
2、一元二次方程解法中的公式法,它的求根公
式是什么?
思考:观察上表,各个方程两根之和、两根之积与方程的系数有
怎样的关系,你能用自己的语言表达吗?
解下列方程,求出各方程的根
并计算
的值,填写下表。
序号
方
程
1
2
3
4
猜想:
1、不解方程,
的两根为
则
则
a
b
-
=
=
=
a
b
-
2
2
a
ac
b
b
ac
b
b
-
-
-
-
+
-
2
4
4
2
2
a
c
=
=
=
·
=
x
x
·
2
1
a
ac
2
4
4
a
ac
b
b
-
-
-
2
2
4
a
ac
b
b
-
+
-
2
2
4
小练习
1、下列各方程中,两根之和与两根之积各是多少?
3、已知一个长方形的长和宽是方程
的两个根,那么这个长方形的周长是
,面积是
.
(2)
(1)
(4)
(5)
(3)
2、请指出下列方程后面括号内的两个数是不是它的两个根。
(1)
(2)
9
解:
解得:
例2
当k为何值时,方程2x2-(k+1)x+k+3=0的两根差为1。
解:设方程两根分别为x1,x2(x1>x2),则x1-x2=1
∵
(x2-x1)2=(x1+x2)2-4x1x2
由根与系数的关系得x1+x2=
,
x1x2=
∴
解得k1=9,k2=
-3
当k=9或-3时,由于△≥0,∴k的值为9或-3。
小练习
.
.
,
,
16
13
1、已知方程3x2-19x+m=0的一个根是1,求它的另一个根及m的值。
2、设x1,x2是方程2x2+4x-3=0的两个根,求(x1+1)(x2+1)的值。
解:设方程的另一个根为x1,
则x1+1=
,
∴
x1=
,
又x1●1=
,
∴
m=
3x1
=
16
解:
由根与系数的关系,得
x1+x2=
-
2
,
x1
·
x2=
∴
(x1+1)(x2+1)
=
x1
x2
+
(x1+x2)+1
=-2+(
)+1=
2、设x1,x2是方程x2-2(k-1)x+k2=0的两个实数根,且x12+x22=4,求k的值。
拓广探索
解:由方程有两个实数根,得
即-8k+4≥0
由根与系数的关系得x1+x2=
2(k-1)
,
x1x2=k2
∴
X12+x22=(x1+x2)2-2x1x2=4(k-1)2-2k2=2k2-8k+4
由X12+x22
=4,得2k2-8k+4=4
解得k1=0
,
k2=4
经检验,
k2=4不合题意,舍去。
∴
k=0
回顾小结
一种方法:
一个定理:
观察、分析、猜测、验证
(从特殊到一般)
韦达定理
布置作业
1、课堂作业:习题第3、4题。
2、思考题:设x1,x2是方程2x2+4x-3=0的两个根,利用根与系数的关系求下列代数式的值:
(1)(x1+1)(x2+1)
(2)x12+x22
感谢各位专家
莅临指导!
同课章节目录
