2020-2021学年河北省沧州市九年级(上)第一次月考数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年河北省沧州市九年级(上)第一次月考数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 586.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 11:57:11 | ||
图片预览




文档简介
2020-2021学年河北省沧州九年级第一学期第一次月考数学试卷
一、选择题(共16个小题,每小题3分,共48分)
1.下列关于x的方程:①ax2+bx+c=0;②x2+﹣3=0;③x2﹣4+x5=0;④3x=x2.其中是一元二次方程的有( )
A.1个
B.2个
C.3个
D.4个
2.一元二次方程(3x﹣1)2=5x化简成一般式后,二次项系数为9,其一次项系数为( )
A.1
B.﹣1
C.﹣11
D.11
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
4.下列图形是中心对称图形的是( )
A.
B.
C.
D.
5.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
A.45
B.60
C.90
D.120
6.把函数y=3x2的图象向右平移2个单位,所得到的新函数的表达式是( )
A.y=3x2﹣2
B.y=3x2+2
C.y=3(x﹣2)2
D.y=3(x+2)2
7.关于二次函数y=2(x﹣2)2+5,下列说法错误的是( )
A.图象与y轴的交点坐标为(0,13)
B.图象的对称轴在y轴的右侧
C.当x>0时,y的值随x值的增大而增大
D.当x=2时,函数有最小值为5
8.a是方程x2+x﹣1=0的一个根,则代数式﹣2a2﹣2a+2020的值是( )
A.2018
B.2019
C.2020
D.2021
9.正方形的边长为3,边长增加x,面积增加y,则y关于x的函数解析式为( )
A.y=(x+3)2
B.y=x2+9
C.y=x2+6x
D.y=3x2+12x
10.如图,在长70m,宽40m的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的,则路宽xm应满足的方程是( )
A.(40﹣x)(70﹣x)=400
B.(40﹣2x)(70﹣3x)=400
C.(40﹣x)(70﹣x)=2400
D.(40﹣2x)(70﹣3x)=2400
11.某商品价格从2017年底到2018年底下降19%,从2018年底到2019年底下降36%,那么此商品价格从2017年底到2019年底平均下降百分率为( )
A.30%
B.28%
C.25.5%
D.20%
12.已知抛物线y=ax2+bx+c与x轴的两个交点坐标是(﹣2,0),(5,0),则一元二次方程ax2+bx+c=0的两个解是( )
A.x1=﹣2,x2=5
B.x1=2,x2=﹣5
C.x1=﹣2,x2=﹣5
D.x1=2,x2=5
13.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②④
14.根据表中的自变量x与函数y的对应值,可判断此函数解析式为( )
x
…
﹣1
0
1
2
…
y
…
﹣1
2
…
A.y=x
B.y=﹣
C.y=(x﹣1)2+2
D.y=﹣(x﹣1)2+2
15.抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤a﹣b+c<0.其中正确的个数是( )
A.2
B.3
C.4
D.5
16.如图,已知点P(m,n)在抛物线y=x(x﹣2)上,针对n的不同取值,所找点P的个数,三人的说法如下:甲:若n=﹣2,则点P的个数为0.乙:若n=﹣1,则点P的个数为1.丙:若n=4,则点P的个数为0.下列判断正确的是( )
A.乙错,丙对
B.甲和乙都错
C.乙对,丙错
D.甲错,丙对
二、填空题(本大题共4个小题,每题5分,共20分)
17.点M(1,a)和点N(b,﹣2)关于原点对称,则(a+b)2020=
.
18.用公式法解一元二次方程,得:x=,则该一元二次方程是
.
19.抛物线y=x2﹣2x﹣3与x轴有两个交点,则原点左侧交点坐标为
.
20.用承重指数W衡量水平放置得长方体木板的最大称重量.实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄,当x=
时,Q=3W薄.
三、解答题(本大题5个小题;共52分。解答应写出文字说明、证明过程或演算步骤)
21.(21分)解方程:
①(x﹣2)2=2;
②x2﹣2x﹣3=0;
③2x2+x+1=0.
22.对于实数a,b,定义新运算“
”:a
b=,例如:4
2,因为4>2,所以4
2=42﹣4×2=8.
(1)求(﹣7)
(﹣2)的值;
(2)若x1,x2是一元二次方程x2﹣5x﹣6=0的两个根,求x1
x2的值.
23.某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量y件与销售单价x(x>10)元之间的关系式;
(2)当销售单价x定为多少,才能使每天所获销售利润最大?最大利润是多少?
24.已知抛物线经过A(1,0),B(5,0),C(0,4),Q四个点,且点Q在x轴下方.
(1)求抛物线的解析式和对称轴;
(2)P是抛物线对称轴上的一点,直接写出满足PA+PC的值为最小的点P坐标;
(3)点Q是否能使得△ABQ的面积和△ABC的面积相等?若能,请直接写出此时的点Q的坐标;若不能,请说明理由.
25.已知△ABC中,∠ABC=90°,∠C=30°,AB=1.若把△ABC绕点B顺时针旋转得到△EBD.
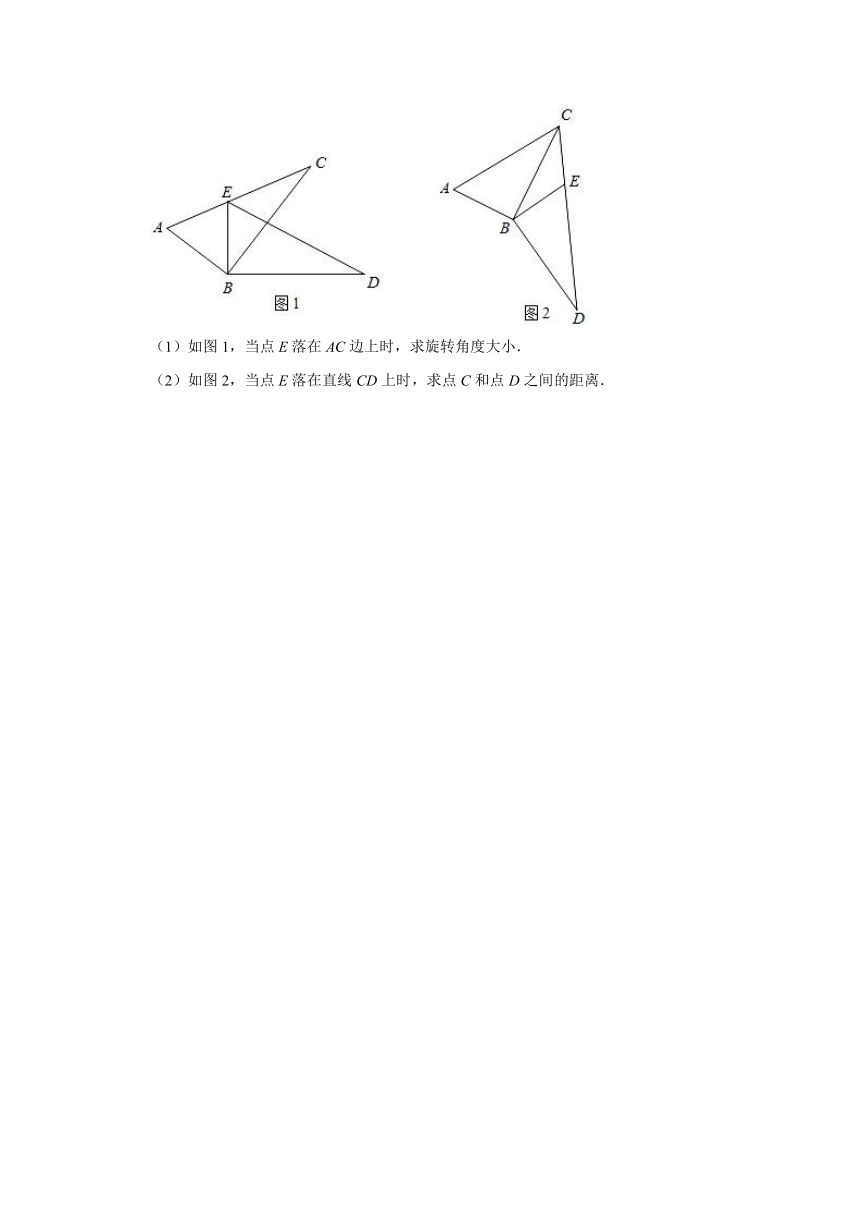
(1)如图1,当点E落在AC边上时,求旋转角度大小.
(2)如图2,当点E落在直线CD上时,求点C和点D之间的距离.
参考答案
一、选择题(本大题共16个小题,每小题3分,共48分,在每小题给出的4个选项中,只有一项符合题目要求)
1.下列关于x的方程:①ax2+bx+c=0;②x2+﹣3=0;③x2﹣4+x5=0;④3x=x2.其中是一元二次方程的有( )
A.1个
B.2个
C.3个
D.4个
解:一元二次方程只有④,共1个,
故选:A.
2.一元二次方程(3x﹣1)2=5x化简成一般式后,二次项系数为9,其一次项系数为( )
A.1
B.﹣1
C.﹣11
D.11
解:一元二次方程(3x﹣1)2=5x的一般形式9x2﹣11x+1=0,
其中二次项系数9,一次项系数﹣11,常数项是1,
故选:C.
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
解:y=x2﹣6x+4=(x﹣3)2﹣5,
故抛物线y=x2﹣6x+4的顶点坐标是:(3,﹣5).
故选:C.
4.下列图形是中心对称图形的是( )
A.
B.
C.
D.
解:A、是轴对称图形,不是中心对称图形,不合题意;
B、是中心对称图形,符合题意;
C、不是中心对称图形,不合题意;
D、是轴对称图形,不是中心对称图形,不合题意.
故选:B.
5.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
A.45
B.60
C.90
D.120
解:该图形被平分成三部分,旋转120°的整数倍,就可以与自身重合,
故n的最小值为120.
故选:D.
6.把函数y=3x2的图象向右平移2个单位,所得到的新函数的表达式是( )
A.y=3x2﹣2
B.y=3x2+2
C.y=3(x﹣2)2
D.y=3(x+2)2
解:二次函数y=3x2的图象向右平移2个单位,
得:y=3(x﹣2)2.
故选:C.
7.关于二次函数y=2(x﹣2)2+5,下列说法错误的是( )
A.图象与y轴的交点坐标为(0,13)
B.图象的对称轴在y轴的右侧
C.当x>0时,y的值随x值的增大而增大
D.当x=2时,函数有最小值为5
解:A、y=2(x﹣2)2+5=2x2﹣8x+13,则图象与y轴的交点坐标为(0,13),原题说法正确,故此选项不合题意;
B、对称轴为x=2,图象的在y轴的右侧,原题说法正确,故此选项不合题意;
C、a=2,开口向上,对称轴为x=2,则当x>2时,y的值随x值的增大而增大,原题说法错误,故此选项符合题意;
D、顶点坐标为(2,5),开口向上,则当x=2时,函数有最小值为5,原题说法正确,故此选项不合题意;
故选:C.
8.a是方程x2+x﹣1=0的一个根,则代数式﹣2a2﹣2a+2020的值是( )
A.2018
B.2019
C.2020
D.2021
解:∵a是方程x2+x﹣1=0的一个根,
∴a2+a﹣1=0,即a2+a=1,
∴﹣2a2﹣2a+2020=﹣2(a2+a)+2020=﹣2×1+2020=2018.
故选:A.
9.正方形的边长为3,边长增加x,面积增加y,则y关于x的函数解析式为( )
A.y=(x+3)2
B.y=x2+9
C.y=x2+6x
D.y=3x2+12x
解:原边长为3的正方形面积为:3×3=9,
边长增加x后边长变为:x+3,
则面积为:(x+3)2,
∴y=(x+3)2﹣9=x2+6x.
故选:C.
10.如图,在长70m,宽40m的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的,则路宽xm应满足的方程是( )
A.(40﹣x)(70﹣x)=400
B.(40﹣2x)(70﹣3x)=400
C.(40﹣x)(70﹣x)=2400
D.(40﹣2x)(70﹣3x)=2400
解:由图可得,
(40﹣2x)(70﹣3x)=40×70×(1﹣),
即(40﹣2x)(70﹣3x)=2400,
故选:D.
11.某商品价格从2017年底到2018年底下降19%,从2018年底到2019年底下降36%,那么此商品价格从2017年底到2019年底平均下降百分率为( )
A.30%
B.28%
C.25.5%
D.20%
解:设此商品价格为a元,从2017年底到2019年底平均下降百分率为x,
根据题意,得:a(1﹣x)2=a(1﹣19%)(1﹣36%),
解得:x1=0.28=28%,x2=﹣1.72(舍去),
答:此商品价格从2017年底到2019年底平均下降百分率为28%.
故选:B.
12.已知抛物线y=ax2+bx+c与x轴的两个交点坐标是(﹣2,0),(5,0),则一元二次方程ax2+bx+c=0的两个解是( )
A.x1=﹣2,x2=5
B.x1=2,x2=﹣5
C.x1=﹣2,x2=﹣5
D.x1=2,x2=5
解:∵抛物线y=ax2+bx+c与x轴的两个交点分别为(﹣2,0),(5,0),
即自变量为﹣2和5时函数值为0,
∴一元二次方程ax2+bx+c=0的根为x1=﹣2,x2=5.
故选:A.
13.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②④
解:①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当t=1.5s时,h=﹣(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
14.根据表中的自变量x与函数y的对应值,可判断此函数解析式为( )
x
…
﹣1
0
1
2
…
y
…
﹣1
2
…
A.y=x
B.y=﹣
C.y=(x﹣1)2+2
D.y=﹣(x﹣1)2+2
解:∵抛物线过点(0,)和(2,),
∴抛物线的对称轴为直线x=1,
∴抛物线的顶点坐标为(1,2)
设抛物线解析式为y=a(x﹣1)2+2,
把(﹣1,﹣1)代入得4a+2=﹣1,解得a=﹣,
∴抛物线解析式为y=﹣(x﹣1)2+2.
故选:D.
15.抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤a﹣b+c<0.其中正确的个数是( )
A.2
B.3
C.4
D.5
解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=﹣1,
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以②正确;
∵抛物线的对称轴为直线x=﹣1,抛物线与x轴的一个交点坐标为(1,0),
∴抛物线与x轴的另一个交点坐标为(﹣3,0),
∴9a﹣3b+c=0,所以③正确;
∵点(﹣0.5,y1)到直线x=﹣1的距离比点(﹣2,y2)到直线x=﹣1的距离小,
而抛物线开口向上,
∴y1<y2;所以④错误;
∵当x=﹣1时,对应y值在x轴下方,
∴a﹣b+c<0,所以⑤正确.
故选:B.
16.如图,已知点P(m,n)在抛物线y=x(x﹣2)上,针对n的不同取值,所找点P的个数,三人的说法如下:甲:若n=﹣2,则点P的个数为0.乙:若n=﹣1,则点P的个数为1.丙:若n=4,则点P的个数为0.下列判断正确的是( )
A.乙错,丙对
B.甲和乙都错
C.乙对,丙错
D.甲错,丙对
解:甲:当n=﹣2时,m(m﹣2)=﹣2,
整理得:m2﹣2m+2=0,
△=(﹣2)2﹣4×1×2=﹣4<0,
方程没有实数根,
即此时点P的个数为0,故甲的说法正确;
乙:当n=﹣1时,m(m﹣2)=﹣1,
整理得:m2﹣2m+1=0,
△=(﹣2)2﹣4×1×1=﹣4=0,
方程有两个相等的实数根,
即此时点P的个数为1,故乙的说法正确;
丙:当n=4时,m(m﹣2)=4,
整理得:m2﹣2m﹣4=0,
△=(﹣2)2﹣4×1×(﹣4)=20>0,
方程有两个不相等的实数根,
即此时点P的个数为2,故丙的说法错误;
故选:C.
二、填空题(本大题共4个小题,每题5分,共20分)
17.点M(1,a)和点N(b,﹣2)关于原点对称,则(a+b)2020= 1 .
解:根据平面内两点关于关于原点对称的点,横坐标与纵坐标都互为相反数,
∴b+1=0,a﹣2=0,
即:b=﹣1且a=2,
∴(a+b)2020=(2﹣1)2020=1.
故答案为:1.
18.用公式法解一元二次方程,得:x=,则该一元二次方程是 3x2+5x+1=0 .
解:根据题意得:a=3,b=5,c=1,
则该一元二次方程是3x2+5x+1=0,
故答案为:3x2+5x+1=0
19.抛物线y=x2﹣2x﹣3与x轴有两个交点,则原点左侧交点坐标为 (﹣1,0) .
解:y=x2﹣2x﹣3,令y=0,
则y=x2﹣2x﹣3=0,解得:x=﹣1或3,
故原点左侧交点坐标为(﹣1,0),
故答案为(﹣1,0).
20.用承重指数W衡量水平放置得长方体木板的最大称重量.实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄,当x= 2 时,Q=3W薄.
解:设W=kx2(k≠0),
∵当x=3时,W=3,
∴3=9k,解得k=,
∴W与x的函数关系式为W=x2;
设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,
∴Q=W厚﹣W薄=(6﹣x)2﹣x2=﹣4x+12,
∴Q与x的函数关系式为Q=﹣4x+12;
∵Q是W薄的3倍,
∴﹣4x+12=3×x2,
整理得,x2+4x﹣12=0,
解得,x1=2,x2=﹣6(不合题意舍去),
故x=2时,Q是W薄的3倍.
故答案为:2
三、解答题(本大题5个小题;共52分。解答应写出文字说明、证明过程或演算步骤)
21.(21分)解方程:
①(x﹣2)2=2;
②x2﹣2x﹣3=0;
③2x2+x+1=0.
解:①∵(x﹣2)2=2,
∴x﹣2=,
∴x1=2+,x2=2﹣;
(2)∵x2﹣2x﹣3=0,
∴(x﹣3)(x+1)=0,
则x﹣3=0或x+1=0,
解得x1=3,x2=﹣1;
③∵a=2,b=1,c=1,
∴Δ=12﹣4×2×1=﹣7<0,
∴此方程无实数根.
22.对于实数a,b,定义新运算“
”:a
b=,例如:4
2,因为4>2,所以4
2=42﹣4×2=8.
(1)求(﹣7)
(﹣2)的值;
(2)若x1,x2是一元二次方程x2﹣5x﹣6=0的两个根,求x1
x2的值.
解:(1)∵﹣7<﹣2,
∴(﹣7)
(﹣2)=14﹣4=10;
(2)方程x2﹣5x﹣6=0变形得:(x+1)(x﹣6)=0,
解得:x=﹣1或x=6,
当x1=﹣1,x2=6时,x1
x2=﹣6﹣36=﹣42;
当x1=6,x2=﹣1时,x1
x2=36+6=42.
23.某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量y件与销售单价x(x>10)元之间的关系式;
(2)当销售单价x定为多少,才能使每天所获销售利润最大?最大利润是多少?
解:(1)y=100﹣10(x﹣10)
=200﹣10x(10≤x<20);
(2)设商店每天获得的利润为W元,则
W=(x﹣8)(200﹣10x)=﹣10x2+280x﹣1600,
当x=14时,w最大=360,
所以当售价为14元时,每天获得的最大利润为360元.
24.已知抛物线经过A(1,0),B(5,0),C(0,4),Q四个点,且点Q在x轴下方.
(1)求抛物线的解析式和对称轴;
(2)P是抛物线对称轴上的一点,直接写出满足PA+PC的值为最小的点P坐标;
(3)点Q是否能使得△ABQ的面积和△ABC的面积相等?若能,请直接写出此时的点Q的坐标;若不能,请说明理由.
解:(1)设抛物线解析式为y=ax2+bx+c,
∵抛物线经过A(1,0),B(5,0),C(0,4),
∴,解得:.
故抛物线解析式为y=x2﹣x+4.
函数的对称轴为:x==3;
(2)连接B、C交对称轴于点P,此时PA+PC的值为最小,
将点B、C的坐标代入一次函数表达式:y=kx+b得:,
解得:,
直线BC的表达式为:y=﹣x+4,
当x=3时,y=,
故点P(3,);
(3)不能,理由:
设点Q的坐标为(x,x2﹣x+4),
∵A(1,0),B(5,0),C(0,4),
∴AB=4,OC=4,
∴S△ABC=AB?OC=×4×4=8,
∵△ABQ的面积和△ABC的面积相等,
∴S△ABQ=AB×|yQ|=2×|yQ|=8,
∵点Q在x轴下方,
∴yQ=﹣x2+x﹣4,
∴2(﹣x2+x﹣4)=8,
整理得:x2﹣6x+10=0,
Δ=36﹣40=﹣4<0,
∴原方程无解,
∴点Q不能使得△ABQ的面积和△ABC的面积相等.
25.已知△ABC中,∠ABC=90°,∠C=30°,AB=1.若把△ABC绕点B顺时针旋转得到△EBD.
(1)如图1,当点E落在AC边上时,求旋转角度大小.
(2)如图2,当点E落在直线CD上时,求点C和点D之间的距离.
解:(1)∵将△ABC绕点B顺时针旋转得到△EBD,
∴AB=BE,
∵∠ABC=90°,∠C=30°,
∴∠A=60°,
∴△ABE是等边三角形,
∴∠ABE=60°,
即旋转角为60°;
(2)∵将△ABC绕点B顺时针旋转得到△EBD,
∴BD=BC,∠D=∠ACB=30°,∠DBE=∠ABC=90°,BE=AB=1
∴∠D=∠BCD=30°,DE=2BE=2,
∴∠CBD=120°,
∴∠CBE=∠CBD﹣∠DBE=120°﹣90°=30°,
∴∠CBE=∠BCD,
∴BE=CE=1,
∴CD=CE+DE=1+2=3.
一、选择题(共16个小题,每小题3分,共48分)
1.下列关于x的方程:①ax2+bx+c=0;②x2+﹣3=0;③x2﹣4+x5=0;④3x=x2.其中是一元二次方程的有( )
A.1个
B.2个
C.3个
D.4个
2.一元二次方程(3x﹣1)2=5x化简成一般式后,二次项系数为9,其一次项系数为( )
A.1
B.﹣1
C.﹣11
D.11
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
4.下列图形是中心对称图形的是( )
A.
B.
C.
D.
5.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
A.45
B.60
C.90
D.120
6.把函数y=3x2的图象向右平移2个单位,所得到的新函数的表达式是( )
A.y=3x2﹣2
B.y=3x2+2
C.y=3(x﹣2)2
D.y=3(x+2)2
7.关于二次函数y=2(x﹣2)2+5,下列说法错误的是( )
A.图象与y轴的交点坐标为(0,13)
B.图象的对称轴在y轴的右侧
C.当x>0时,y的值随x值的增大而增大
D.当x=2时,函数有最小值为5
8.a是方程x2+x﹣1=0的一个根,则代数式﹣2a2﹣2a+2020的值是( )
A.2018
B.2019
C.2020
D.2021
9.正方形的边长为3,边长增加x,面积增加y,则y关于x的函数解析式为( )
A.y=(x+3)2
B.y=x2+9
C.y=x2+6x
D.y=3x2+12x
10.如图,在长70m,宽40m的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的,则路宽xm应满足的方程是( )
A.(40﹣x)(70﹣x)=400
B.(40﹣2x)(70﹣3x)=400
C.(40﹣x)(70﹣x)=2400
D.(40﹣2x)(70﹣3x)=2400
11.某商品价格从2017年底到2018年底下降19%,从2018年底到2019年底下降36%,那么此商品价格从2017年底到2019年底平均下降百分率为( )
A.30%
B.28%
C.25.5%
D.20%
12.已知抛物线y=ax2+bx+c与x轴的两个交点坐标是(﹣2,0),(5,0),则一元二次方程ax2+bx+c=0的两个解是( )
A.x1=﹣2,x2=5
B.x1=2,x2=﹣5
C.x1=﹣2,x2=﹣5
D.x1=2,x2=5
13.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②④
14.根据表中的自变量x与函数y的对应值,可判断此函数解析式为( )
x
…
﹣1
0
1
2
…
y
…
﹣1
2
…
A.y=x
B.y=﹣
C.y=(x﹣1)2+2
D.y=﹣(x﹣1)2+2
15.抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤a﹣b+c<0.其中正确的个数是( )
A.2
B.3
C.4
D.5
16.如图,已知点P(m,n)在抛物线y=x(x﹣2)上,针对n的不同取值,所找点P的个数,三人的说法如下:甲:若n=﹣2,则点P的个数为0.乙:若n=﹣1,则点P的个数为1.丙:若n=4,则点P的个数为0.下列判断正确的是( )
A.乙错,丙对
B.甲和乙都错
C.乙对,丙错
D.甲错,丙对
二、填空题(本大题共4个小题,每题5分,共20分)
17.点M(1,a)和点N(b,﹣2)关于原点对称,则(a+b)2020=
.
18.用公式法解一元二次方程,得:x=,则该一元二次方程是
.
19.抛物线y=x2﹣2x﹣3与x轴有两个交点,则原点左侧交点坐标为
.
20.用承重指数W衡量水平放置得长方体木板的最大称重量.实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄,当x=
时,Q=3W薄.
三、解答题(本大题5个小题;共52分。解答应写出文字说明、证明过程或演算步骤)
21.(21分)解方程:
①(x﹣2)2=2;
②x2﹣2x﹣3=0;
③2x2+x+1=0.
22.对于实数a,b,定义新运算“
”:a
b=,例如:4
2,因为4>2,所以4
2=42﹣4×2=8.
(1)求(﹣7)
(﹣2)的值;
(2)若x1,x2是一元二次方程x2﹣5x﹣6=0的两个根,求x1
x2的值.
23.某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量y件与销售单价x(x>10)元之间的关系式;
(2)当销售单价x定为多少,才能使每天所获销售利润最大?最大利润是多少?
24.已知抛物线经过A(1,0),B(5,0),C(0,4),Q四个点,且点Q在x轴下方.
(1)求抛物线的解析式和对称轴;
(2)P是抛物线对称轴上的一点,直接写出满足PA+PC的值为最小的点P坐标;
(3)点Q是否能使得△ABQ的面积和△ABC的面积相等?若能,请直接写出此时的点Q的坐标;若不能,请说明理由.
25.已知△ABC中,∠ABC=90°,∠C=30°,AB=1.若把△ABC绕点B顺时针旋转得到△EBD.
(1)如图1,当点E落在AC边上时,求旋转角度大小.
(2)如图2,当点E落在直线CD上时,求点C和点D之间的距离.
参考答案
一、选择题(本大题共16个小题,每小题3分,共48分,在每小题给出的4个选项中,只有一项符合题目要求)
1.下列关于x的方程:①ax2+bx+c=0;②x2+﹣3=0;③x2﹣4+x5=0;④3x=x2.其中是一元二次方程的有( )
A.1个
B.2个
C.3个
D.4个
解:一元二次方程只有④,共1个,
故选:A.
2.一元二次方程(3x﹣1)2=5x化简成一般式后,二次项系数为9,其一次项系数为( )
A.1
B.﹣1
C.﹣11
D.11
解:一元二次方程(3x﹣1)2=5x的一般形式9x2﹣11x+1=0,
其中二次项系数9,一次项系数﹣11,常数项是1,
故选:C.
3.抛物线y=x2﹣6x+4的顶点坐标是( )
A.(3,5)
B.(﹣3,5)
C.(3,﹣5)
D.(﹣3,﹣5)
解:y=x2﹣6x+4=(x﹣3)2﹣5,
故抛物线y=x2﹣6x+4的顶点坐标是:(3,﹣5).
故选:C.
4.下列图形是中心对称图形的是( )
A.
B.
C.
D.
解:A、是轴对称图形,不是中心对称图形,不合题意;
B、是中心对称图形,符合题意;
C、不是中心对称图形,不合题意;
D、是轴对称图形,不是中心对称图形,不合题意.
故选:B.
5.风力发电机可以在风力作用下发电.如图的转子叶片图案绕中心旋转n°后能与原来的图案重合,那么n的值可能是( )
A.45
B.60
C.90
D.120
解:该图形被平分成三部分,旋转120°的整数倍,就可以与自身重合,
故n的最小值为120.
故选:D.
6.把函数y=3x2的图象向右平移2个单位,所得到的新函数的表达式是( )
A.y=3x2﹣2
B.y=3x2+2
C.y=3(x﹣2)2
D.y=3(x+2)2
解:二次函数y=3x2的图象向右平移2个单位,
得:y=3(x﹣2)2.
故选:C.
7.关于二次函数y=2(x﹣2)2+5,下列说法错误的是( )
A.图象与y轴的交点坐标为(0,13)
B.图象的对称轴在y轴的右侧
C.当x>0时,y的值随x值的增大而增大
D.当x=2时,函数有最小值为5
解:A、y=2(x﹣2)2+5=2x2﹣8x+13,则图象与y轴的交点坐标为(0,13),原题说法正确,故此选项不合题意;
B、对称轴为x=2,图象的在y轴的右侧,原题说法正确,故此选项不合题意;
C、a=2,开口向上,对称轴为x=2,则当x>2时,y的值随x值的增大而增大,原题说法错误,故此选项符合题意;
D、顶点坐标为(2,5),开口向上,则当x=2时,函数有最小值为5,原题说法正确,故此选项不合题意;
故选:C.
8.a是方程x2+x﹣1=0的一个根,则代数式﹣2a2﹣2a+2020的值是( )
A.2018
B.2019
C.2020
D.2021
解:∵a是方程x2+x﹣1=0的一个根,
∴a2+a﹣1=0,即a2+a=1,
∴﹣2a2﹣2a+2020=﹣2(a2+a)+2020=﹣2×1+2020=2018.
故选:A.
9.正方形的边长为3,边长增加x,面积增加y,则y关于x的函数解析式为( )
A.y=(x+3)2
B.y=x2+9
C.y=x2+6x
D.y=3x2+12x
解:原边长为3的正方形面积为:3×3=9,
边长增加x后边长变为:x+3,
则面积为:(x+3)2,
∴y=(x+3)2﹣9=x2+6x.
故选:C.
10.如图,在长70m,宽40m的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的,则路宽xm应满足的方程是( )
A.(40﹣x)(70﹣x)=400
B.(40﹣2x)(70﹣3x)=400
C.(40﹣x)(70﹣x)=2400
D.(40﹣2x)(70﹣3x)=2400
解:由图可得,
(40﹣2x)(70﹣3x)=40×70×(1﹣),
即(40﹣2x)(70﹣3x)=2400,
故选:D.
11.某商品价格从2017年底到2018年底下降19%,从2018年底到2019年底下降36%,那么此商品价格从2017年底到2019年底平均下降百分率为( )
A.30%
B.28%
C.25.5%
D.20%
解:设此商品价格为a元,从2017年底到2019年底平均下降百分率为x,
根据题意,得:a(1﹣x)2=a(1﹣19%)(1﹣36%),
解得:x1=0.28=28%,x2=﹣1.72(舍去),
答:此商品价格从2017年底到2019年底平均下降百分率为28%.
故选:B.
12.已知抛物线y=ax2+bx+c与x轴的两个交点坐标是(﹣2,0),(5,0),则一元二次方程ax2+bx+c=0的两个解是( )
A.x1=﹣2,x2=5
B.x1=2,x2=﹣5
C.x1=﹣2,x2=﹣5
D.x1=2,x2=5
解:∵抛物线y=ax2+bx+c与x轴的两个交点分别为(﹣2,0),(5,0),
即自变量为﹣2和5时函数值为0,
∴一元二次方程ax2+bx+c=0的根为x1=﹣2,x2=5.
故选:A.
13.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;
②小球运动的时间为6s;
③小球抛出3秒时,速度为0;
④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④
B.①②
C.②③④
D.②④
解:①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当t=1.5s时,h=﹣(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
14.根据表中的自变量x与函数y的对应值,可判断此函数解析式为( )
x
…
﹣1
0
1
2
…
y
…
﹣1
2
…
A.y=x
B.y=﹣
C.y=(x﹣1)2+2
D.y=﹣(x﹣1)2+2
解:∵抛物线过点(0,)和(2,),
∴抛物线的对称轴为直线x=1,
∴抛物线的顶点坐标为(1,2)
设抛物线解析式为y=a(x﹣1)2+2,
把(﹣1,﹣1)代入得4a+2=﹣1,解得a=﹣,
∴抛物线解析式为y=﹣(x﹣1)2+2.
故选:D.
15.抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤a﹣b+c<0.其中正确的个数是( )
A.2
B.3
C.4
D.5
解:∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴为直线x=﹣=﹣1,
∴b=2a>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,所以①错误;
∵抛物线与x轴有2个交点,
∴Δ=b2﹣4ac>0,所以②正确;
∵抛物线的对称轴为直线x=﹣1,抛物线与x轴的一个交点坐标为(1,0),
∴抛物线与x轴的另一个交点坐标为(﹣3,0),
∴9a﹣3b+c=0,所以③正确;
∵点(﹣0.5,y1)到直线x=﹣1的距离比点(﹣2,y2)到直线x=﹣1的距离小,
而抛物线开口向上,
∴y1<y2;所以④错误;
∵当x=﹣1时,对应y值在x轴下方,
∴a﹣b+c<0,所以⑤正确.
故选:B.
16.如图,已知点P(m,n)在抛物线y=x(x﹣2)上,针对n的不同取值,所找点P的个数,三人的说法如下:甲:若n=﹣2,则点P的个数为0.乙:若n=﹣1,则点P的个数为1.丙:若n=4,则点P的个数为0.下列判断正确的是( )
A.乙错,丙对
B.甲和乙都错
C.乙对,丙错
D.甲错,丙对
解:甲:当n=﹣2时,m(m﹣2)=﹣2,
整理得:m2﹣2m+2=0,
△=(﹣2)2﹣4×1×2=﹣4<0,
方程没有实数根,
即此时点P的个数为0,故甲的说法正确;
乙:当n=﹣1时,m(m﹣2)=﹣1,
整理得:m2﹣2m+1=0,
△=(﹣2)2﹣4×1×1=﹣4=0,
方程有两个相等的实数根,
即此时点P的个数为1,故乙的说法正确;
丙:当n=4时,m(m﹣2)=4,
整理得:m2﹣2m﹣4=0,
△=(﹣2)2﹣4×1×(﹣4)=20>0,
方程有两个不相等的实数根,
即此时点P的个数为2,故丙的说法错误;
故选:C.
二、填空题(本大题共4个小题,每题5分,共20分)
17.点M(1,a)和点N(b,﹣2)关于原点对称,则(a+b)2020= 1 .
解:根据平面内两点关于关于原点对称的点,横坐标与纵坐标都互为相反数,
∴b+1=0,a﹣2=0,
即:b=﹣1且a=2,
∴(a+b)2020=(2﹣1)2020=1.
故答案为:1.
18.用公式法解一元二次方程,得:x=,则该一元二次方程是 3x2+5x+1=0 .
解:根据题意得:a=3,b=5,c=1,
则该一元二次方程是3x2+5x+1=0,
故答案为:3x2+5x+1=0
19.抛物线y=x2﹣2x﹣3与x轴有两个交点,则原点左侧交点坐标为 (﹣1,0) .
解:y=x2﹣2x﹣3,令y=0,
则y=x2﹣2x﹣3=0,解得:x=﹣1或3,
故原点左侧交点坐标为(﹣1,0),
故答案为(﹣1,0).
20.用承重指数W衡量水平放置得长方体木板的最大称重量.实验发现:木板承重指数W与木板厚度x(厘米)的平方成正比,当x=3时,W=3.选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为x(厘米),Q=W厚﹣W薄,当x= 2 时,Q=3W薄.
解:设W=kx2(k≠0),
∵当x=3时,W=3,
∴3=9k,解得k=,
∴W与x的函数关系式为W=x2;
设薄板的厚度为x厘米,则厚板的厚度为(6﹣x)厘米,
∴Q=W厚﹣W薄=(6﹣x)2﹣x2=﹣4x+12,
∴Q与x的函数关系式为Q=﹣4x+12;
∵Q是W薄的3倍,
∴﹣4x+12=3×x2,
整理得,x2+4x﹣12=0,
解得,x1=2,x2=﹣6(不合题意舍去),
故x=2时,Q是W薄的3倍.
故答案为:2
三、解答题(本大题5个小题;共52分。解答应写出文字说明、证明过程或演算步骤)
21.(21分)解方程:
①(x﹣2)2=2;
②x2﹣2x﹣3=0;
③2x2+x+1=0.
解:①∵(x﹣2)2=2,
∴x﹣2=,
∴x1=2+,x2=2﹣;
(2)∵x2﹣2x﹣3=0,
∴(x﹣3)(x+1)=0,
则x﹣3=0或x+1=0,
解得x1=3,x2=﹣1;
③∵a=2,b=1,c=1,
∴Δ=12﹣4×2×1=﹣7<0,
∴此方程无实数根.
22.对于实数a,b,定义新运算“
”:a
b=,例如:4
2,因为4>2,所以4
2=42﹣4×2=8.
(1)求(﹣7)
(﹣2)的值;
(2)若x1,x2是一元二次方程x2﹣5x﹣6=0的两个根,求x1
x2的值.
解:(1)∵﹣7<﹣2,
∴(﹣7)
(﹣2)=14﹣4=10;
(2)方程x2﹣5x﹣6=0变形得:(x+1)(x﹣6)=0,
解得:x=﹣1或x=6,
当x1=﹣1,x2=6时,x1
x2=﹣6﹣36=﹣42;
当x1=6,x2=﹣1时,x1
x2=36+6=42.
23.某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量y件与销售单价x(x>10)元之间的关系式;
(2)当销售单价x定为多少,才能使每天所获销售利润最大?最大利润是多少?
解:(1)y=100﹣10(x﹣10)
=200﹣10x(10≤x<20);
(2)设商店每天获得的利润为W元,则
W=(x﹣8)(200﹣10x)=﹣10x2+280x﹣1600,
当x=14时,w最大=360,
所以当售价为14元时,每天获得的最大利润为360元.
24.已知抛物线经过A(1,0),B(5,0),C(0,4),Q四个点,且点Q在x轴下方.
(1)求抛物线的解析式和对称轴;
(2)P是抛物线对称轴上的一点,直接写出满足PA+PC的值为最小的点P坐标;
(3)点Q是否能使得△ABQ的面积和△ABC的面积相等?若能,请直接写出此时的点Q的坐标;若不能,请说明理由.
解:(1)设抛物线解析式为y=ax2+bx+c,
∵抛物线经过A(1,0),B(5,0),C(0,4),
∴,解得:.
故抛物线解析式为y=x2﹣x+4.
函数的对称轴为:x==3;
(2)连接B、C交对称轴于点P,此时PA+PC的值为最小,
将点B、C的坐标代入一次函数表达式:y=kx+b得:,
解得:,
直线BC的表达式为:y=﹣x+4,
当x=3时,y=,
故点P(3,);
(3)不能,理由:
设点Q的坐标为(x,x2﹣x+4),
∵A(1,0),B(5,0),C(0,4),
∴AB=4,OC=4,
∴S△ABC=AB?OC=×4×4=8,
∵△ABQ的面积和△ABC的面积相等,
∴S△ABQ=AB×|yQ|=2×|yQ|=8,
∵点Q在x轴下方,
∴yQ=﹣x2+x﹣4,
∴2(﹣x2+x﹣4)=8,
整理得:x2﹣6x+10=0,
Δ=36﹣40=﹣4<0,
∴原方程无解,
∴点Q不能使得△ABQ的面积和△ABC的面积相等.
25.已知△ABC中,∠ABC=90°,∠C=30°,AB=1.若把△ABC绕点B顺时针旋转得到△EBD.
(1)如图1,当点E落在AC边上时,求旋转角度大小.
(2)如图2,当点E落在直线CD上时,求点C和点D之间的距离.
解:(1)∵将△ABC绕点B顺时针旋转得到△EBD,
∴AB=BE,
∵∠ABC=90°,∠C=30°,
∴∠A=60°,
∴△ABE是等边三角形,
∴∠ABE=60°,
即旋转角为60°;
(2)∵将△ABC绕点B顺时针旋转得到△EBD,
∴BD=BC,∠D=∠ACB=30°,∠DBE=∠ABC=90°,BE=AB=1
∴∠D=∠BCD=30°,DE=2BE=2,
∴∠CBD=120°,
∴∠CBE=∠CBD﹣∠DBE=120°﹣90°=30°,
∴∠CBE=∠BCD,
∴BE=CE=1,
∴CD=CE+DE=1+2=3.
同课章节目录
