2021-2022学年八年级数学苏科版上册1.3探索全等三角形的条件综合强化提优(三)(word版、含解析)
文档属性
| 名称 | 2021-2022学年八年级数学苏科版上册1.3探索全等三角形的条件综合强化提优(三)(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 959.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 18:35:12 | ||
图片预览




文档简介
2021-2022学期苏科版八年级数学上《1.3探索全等三角形的条件》综合强化提优(三)
(时间:90分钟
满分:120分)
一.选择题(每小题2分
共30分)
1.
两个三角形的两条边及其中一条边的对角对应相等,则下列四个命题中,真命题的个数是(
)个①这两个三角形全等;
②相等的角为锐角时全等③相等的角为钝角对全等;
④相等的角为直角时全等
A.0
B.1
C.2
D.3
2.在下列定理中假命题是(
)
A.一个等腰三角形必能分成两个全等的直角三角形
B.一个直角三角形必能分成两个等腰三角形
C.两个全等的直角三角形必能拼成一个等腰三角形
D.两个等腰三角形必能拼成一个直角三角形
3.如图,Rt△ABC中,∠B=90°,∠ACB=60°,延长BC到D,使CD=AC则AC:BD=(
)
A.1:1
B.3:1
C.4:1
D.2:3
第3题图
第4题图
第6题图
第8题图
4.如图,在Rt△ABC中,∠ACB=90°,CD、CE,分别是斜边AB上的高与中线,CF是∠ACB的平分线.则∠1与∠2的关系是(
)
A.∠1<∠2
B.∠1=∠2;
C.∠1>∠2
D.不能确定
5.在直角三角形ABC中,若∠C=90°,D是BC边上的一点,且AD=2CD,则∠ADB的度数是(
)
A.30°
B.60°
C.120°
D.150°
6.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再取BF的垂线DE,使点A,C,E在同一条直线上(如图所示),可以证明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长.则判定△EDC≌△ABC的理由是(
)
A.
SAS
B.
ASA
C.
SSS
D.
HL
7.下列条件中,不能判定两个直角三角形全等的是(
)
A.
一条直角边和一个锐角分别相等
B.
两条直角边对应相等
C.
斜边和一条直角边对应相等
D.
斜边和一个锐角对应相等
8.如图,已知△ABC,求作一点P,使点P到∠BAC两边的距离相等,且PA=PB.下列确定点P的方法中,正确的是(
)
A.
P是∠BAC,∠ABC两角平分线的交点
B.
P为∠BAC的平分线与AB的垂直平分线的交点
C.
P为AB,AC两边上的高线的交点
D.
P为AC,AB两边的垂直平分线的交点
9.如图,直线l1,l2,l3表示相交的道路,现要选定一个货物中转站,要求该站到三条道路的距离相等,可供选择的点有(
)
A.
1处
B.
2处
C.
3处
D.
4处
第9题图
第11题图
第12题图
第14题图
10.下列说法正确的有( )
①角平分线上任意一点到角两边的距离相等;②到一个角两边的距离相等的点在这个角的平分线上;③三角形三个角平分线的交点到三个顶点的距离相等;④三角形三条角平分线的交点到三边的距离相等.
A.1个
B.2个
C.3个
D.4个
11.如图,PD⊥AB,PE⊥AC,垂足分别为D,E,且PD=PE,判定△APD与△APE全等的理由是(
)
A.SAS
B.AAS
C.SSS
D.HL
12.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是
(
)
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
13.不能使两个直角三角形全等的条件是(
)
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和两条直角边对应相等
D.两个锐角对应相等
14.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为
(
)
A.11
B.5.5
C.7
D.3.5
15.如(1)图,由已知AB⊥BD,ED⊥BD,AB=CD,BC=DE可证得AC⊥CE,若将CD沿CB方向平移到图(2)(3)(4)(5)的情形,其余条件不变,则这四种情况下,结论AC1⊥C2
E仍然成立的有(
)
A.2个
B.2个
C.3个
D.4个
二.填空题(每小题2分
共30分)
16.已知在△ABC和△A′B′C′中,∠C=∠C′=90°,要使△ABC≌△A′B′C′,可以添加条件:
_____________________________________________.
17.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌____,全等的根据是___.
第17题图
第19题图
第20题图
第21题图
18.判定两直角三角形全等的各种条件:(1)一锐角和一边对应相等(2)两边对应相等(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是____________
19.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF的度数是______,∠FBC的度数是________
20.如图,Rt△ABC中,AC=BC=6,D为AB的中点,DE⊥DF,DE,DF分别交AC、BC于点E、F.若已知DE=4,则四边形DECF的周长为______.
21.如图,在△ABC中,∠ABC=45°,F是高线AD和BE的交点,CD=4,则线段DF的长度为
22.如图,在△ABC和△ABD中,∠C=∠D=90°,若利甩“AAS”证明△ABC≌△ABD,则需要添加一个条件
或
;若利用“HL”证明:△ABC≌△ABD,则需要添加一个条件
或
.
第22题图
第23题图
第24题图
第25题图
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=
°.
24..如图,有两个长度相同的滑梯
(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=
度.
25.如图,在△ABC中,AD⊥BC于D,AD与BE相交于H,且BH=AC,DH=DC,那么∠ABC=
°.
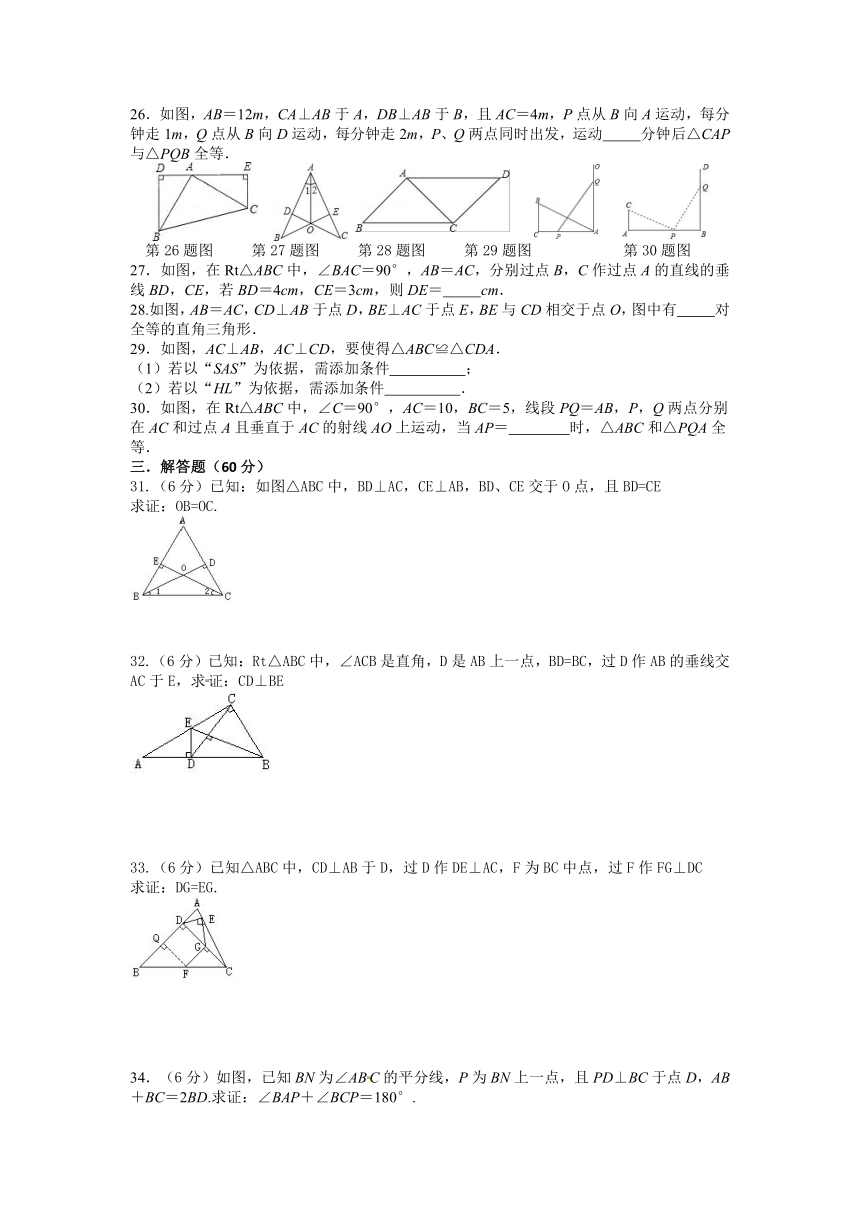
26.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后△CAP与△PQB全等.
第26题图
第27题图
第28题图
第29题图
第30题图
27.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=
cm.
28.如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,图中有
对全等的直角三角形.
29.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件
;
(2)若以“HL”为依据,需添加条件
.
30.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC和△PQA全等.
三.解答题(60分)
31.(6分)已知:如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE
求证:OB=OC.
32.(6分)已知:Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,求证:CD⊥BE
33.(6分)已知△ABC中,CD⊥AB于D,过D作DE⊥AC,F为BC中点,过F作FG⊥DC
求证:DG=EG.
34.(6分)如图,已知BN为∠ABC的平分线,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.求证:∠BAP+∠BCP=180°.
35.(6分)如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.
36.(6分)如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
37.(8分)如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线.点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上.(2)若AC=5,BC=12,求OE的长.
38..(8分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
39.(8分)CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;EF
|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
教师样卷
一.选择题(每小题2分
共30分)
1.
两个三角形的两条边及其中一条边的对角对应相等,则下列四个命题中,真命题的个数是(
C
)个①这两个三角形全等;
②相等的角为锐角时全等③相等的角为钝角对全等;
④相等的角为直角时全等
A.0
B.1
C.2
D.3
2.在下列定理中假命题是(
D
)
A.一个等腰三角形必能分成两个全等的直角三角形
B.一个直角三角形必能分成两个等腰三角形
C.两个全等的直角三角形必能拼成一个等腰三角形
D.两个等腰三角形必能拼成一个直角三角形
3.如图,Rt△ABC中,∠B=90°,∠ACB=60°,延长BC到D,使CD=AC则AC:BD=(
D
)
A.1:1
B.3:1
C.4:1
D.2:3
【解析】设BC=x则AC=2x,CD=2x
∴BD=3x∴AC:BD=2:3
第3题图
第4题图
第6题图
第8题图
4.如图,在Rt△ABC中,∠ACB=90°,CD、CE,分别是斜边AB上的高与中线,CF是∠ACB的平分线.则∠1与∠2的关系是(
B
)
A.∠1<∠2
B.∠1=∠2;
C.∠1>∠2
D.不能确定
【解析】∵CE为△ABC中线,∴AE=EC∴∠3=∠A∵CF平分∠ACB∴∠ACF=∠FCB
即∠3+∠1=∠2+∠4∵CD⊥AB,∠ACB=90°∴∠4=∠A∴∠3+∠1=∠2+∠A∴∠1=∠2
5.在直角三角形ABC中,若∠C=90°,D是BC边上的一点,且AD=2CD,则∠ADB的度数是(
C
)
A.30°
B.60°
C.120°
D.150°
【解析】∠ADC=60°∴∠ADB=120°
6.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再取BF的垂线DE,使点A,C,E在同一条直线上(如图所示),可以证明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长.则判定△EDC≌△ABC的理由是(B)
A.
SAS
B.
ASA
C.
SSS
D.
HL
7.下列条件中,不能判定两个直角三角形全等的是(A)
A.
一条直角边和一个锐角分别相等
B.
两条直角边对应相等
C.
斜边和一条直角边对应相等
D.
斜边和一个锐角对应相等
8.如图,已知△ABC,求作一点P,使点P到∠BAC两边的距离相等,且PA=PB.下列确定点P的方法中,正确的是(B)
A.
P是∠BAC,∠ABC两角平分线的交点
B.
P为∠BAC的平分线与AB的垂直平分线的交点
C.
P为AB,AC两边上的高线的交点
D.
P为AC,AB两边的垂直平分线的交点
9.如图,直线l1,l2,l3表示相交的道路,现要选定一个货物中转站,要求该站到三条道路的距离相等,可供选择的点有(D)
A.
1处
B.
2处
C.
3处
D.
4处
【解】 如解图,作角平分线,利用角平分线上的点到角的两边的距离相等,可知P1,P2,P3,P4都满足条件.
第9题图
第11题图
第12题图
第14题图
10.下列说法正确的有( B )
①角平分线上任意一点到角两边的距离相等;②到一个角两边的距离相等的点在这个角的平分线上;③三角形三个角平分线的交点到三个顶点的距离相等;④三角形三条角平分线的交点到三边的距离相等.
A.1个
B.2个
C.3个
D.4个
11.如图,PD⊥AB,PE⊥AC,垂足分别为D,E,且PD=PE,判定△APD与△APE全等的理由是(
D
)
A.SAS
B.AAS
C.SSS
D.HL
12.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是
(
A
)
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
13.不能使两个直角三角形全等的条件是(
D
)
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和两条直角边对应相等
D.两个锐角对应相等
14.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为
(
B
)
A.11
B.5.5
C.7
D.3.5
15.如(1)图,由已知AB⊥BD,ED⊥BD,AB=CD,BC=DE可证得AC⊥CE,若将CD沿CB方向平移到图(2)(3)(4)(5)的情形,其余条件不变,则这四种情况下,结论AC1⊥C2
E仍然成立的有(
D
)
A.2个
B.2个
C.3个
D.4个
二.填空题(每小题2分
共30分)
16.已知在△ABC和△A′B′C′中,∠C=∠C′=90°,要使△ABC≌△A′B′C′,可以添加条件:AC=A′C′,AB=A′B′(答案不唯一).
17.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌__△DFE___,全等的根据是__HL___.
第17题图
第19题图
第20题图
第21题图
18.判定两直角三角形全等的各种条件:(1)一锐角和一边对应相等(2)两边对应相等(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是(1)(2)
19.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF的度数是20°,∠FBC的度数是40°
20.如图,Rt△ABC中,AC=BC=6,D为AB的中点,DE⊥DF,DE,DF分别交AC、BC于点E、F.若已知DE=4,则四边形DECF的周长为14
21.如图,在△ABC中,∠ABC=45°,F是高线AD和BE的交点,CD=4,则线段DF的长度为
4
22.如图,在△ABC和△ABD中,∠C=∠D=90°,若利甩“AAS”证明△ABC≌△ABD,则需要添加一个条件
或
;若利用“HL”证明:△ABC≌△ABD,则需要添加一个条件
或
.
【答案】∠CAB=∠DAB
∠CBA=∠DBA
AC=AD
BC=BD
第22题图
第23题图
第24题图
第25题图
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=
35
°.
24..如图,有两个长度相同的滑梯
(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=
90
度.
25.如图,在△ABC中,AD⊥BC于D,AD与BE相交于H,且BH=AC,DH=DC,那么∠ABC=
45
°.
26.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
4 分钟后△CAP与△PQB全等.
解:∵CA⊥AB于A,DB⊥AB于B,∴∠A=∠B=90°,设运动x分钟后△CAP与△PQB全等;则BP=xm,BQ=2xm,则AP=(12﹣x)m,分两种情况:①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,∴△CAP≌△PBQ;②若BP=AP,则12﹣x=x,解得:x=6,BQ=12≠AC,此时△CAP与△PQB不全等;综上所述:运动4分钟后△CAP与△PQB全等;故答案为:4.
第26题图
第27题图
第28题图
第29题图
第30题图
27.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= 7
cm.
解:∵在Rt△ABC中,∠BAC=90°,∠ADB=∠AEC=90∴∠BAD+∠EAC=90°,∠BAD+∠B=90°∴∠EAC=∠B∵AB=AC∴△ABD≌△ACE(AAS)∴AD=CE,BD=AE∴DE=AD+AE=CE+BD=7cm.故填7.
28.如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,图中有 3
对全等的直角三角形.
解:∵CD⊥AB,BE⊥AC,∴∠AEB=∠ADC=90°,在Rt△ABE和△Rt△ACD中
∴Rt△ABE≌△Rt△ACD(AAS),∴AD=AE,在Rt△AOD和Rt△AOE中∴Rt△AOD≌Rt△AOE(HL),∴OD=OE,在Rt△BOD和Rt△COE中
∴Rt△BOD≌Rt△COE(ASA),∴全等的直角三角形共有3对,故答案为:3.
29.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件
AB=CD
;
(2)若以“HL”为依据,需添加条件
AD=BC
.
解:(1)若以“SAS”为依据,需添加条件:AB=CD;∵AC⊥AB,AC⊥CD,∴∠BAC=90°,∠DCA=90°,∴∠BAC=∠DCA,在△ABC和△CDA中,∵,
∴△ABC≌△CDA(SAS);
(2)若以“HL”为依据,需添加条件:AD=BC;在Rt△ABC和Rt△CDA中,
∴Rt△ABC≌Rt△CDA(HL).
30.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
5或10
时,△ABC和△PQA全等.
解:当AP=5或10时,△ABC和△PQA全等,理由是:∵∠C=90°,AO⊥AC,∴∠C=∠QAP=90°,①当AP=5=BC时,在Rt△ACB和Rt△QAP中∴Rt△ACB≌Rt△QAP(HL),②当AP=10=AC时,在Rt△ACB和Rt△PAQ中∴Rt△ACB≌Rt△PAQ(HL),故答案为:5或10.
三.解答题(60分)
31.(6分)已知:如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE
求证:OB=OC.
证明:∵CE⊥AB,BD⊥AC,则∠BEC=∠CDB=90°∴在Rt△BCE与Rt△CBD中
∴Rt△BCE≌Rt△CBD(HL)∴∠1=∠2,∴OB=OC
32.(6分)已知:Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,求证:CD⊥BE
证明:∵DE⊥AB∴∠BDE=90°,∵∠ACB=90°∴在Rt△DEB中与Rt△CEB中BD=BC
BE=BE∴Rt△DEB≌Rt△CEB(HL)∴DE=EC又∵BD=BC∴E、B在CD的垂直平分线上即BE⊥CD.
33.(6分)已知△ABC中,CD⊥AB于D,过D作DE⊥AC,F为BC中点,过F作FG⊥DC
求证:DG=EG.
证明:作FQ⊥BD于Q,∴∠FQB=90°∵DE⊥AC∴∠DEC=90°∵FG⊥CD
CD⊥BD
∴BD//FG,∠BDC=∠FGC=90°∴QF//CD∴QF=DG,∴∠B=∠GFC∵F为BC中点∴BF=FC
在Rt△BQF与Rt△FGC中∴△BQF≌△FGC(AAS)∴QF=GC
∵QF=DG
∴DG=GC∴在Rt△DEC中,∵G为DC中点∴DG=EG
34.(6分)如图,已知BN为∠ABC的平分线,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.求证:∠BAP+∠BCP=180°.
【解】 过点P作PE⊥射线BA于点E.∵BN平分∠ABC,点P在BN上,PD⊥BC,PE⊥AB,∴PE=PD,∠BEP=∠BDP=90°.在Rt△PBE和Rt△PBD中,∵PB=PB,PE=PD,
∴Rt△PBE≌Rt△PBD(HL),∴BE=BD.∵AB+BC=2BD,AB=BE-AE,BC=BD+CD,
∴BE-AE+BD+CD=2BD,∴AE=CD.在△PEA和△PDC中,∵∴△PEA≌△PDC(SAS),∴∠PAE=∠PCD,即∠PAE=∠BCP.∵∠BAP+∠PAE=180°,∴∠BAP+∠BCP=180°.
35.(6分)如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.
证明:∵∠BAC=90°,CE⊥AE,BD⊥AE,∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°.∴∠ABD=∠DAC.∵在△ABD和△CAE中,
∴△ABD≌△CAE(AAS).∴BD=AE,EC=AD.∵AE=AD+DE,∴BD=EC+ED.
36.(6分)如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
解:根据三角形全等的判定方法HL可知:①当P运动到AP=BC时,∵∠C=∠QAP=90°,在Rt△ABC与Rt△QPA中,∴Rt△ABC≌Rt△QPA(HL),即AP=BC=5cm;
②当P运动到与C点重合时,AP=AC,在Rt△ABC与Rt△QPA中,,∴Rt△QAP≌Rt△BCA(HL),即AP=AC=10cm,∴当点P与点C重合时,△ABC才能和△APQ全等.综上所述,当点P位于AC的中点处或当点P与点C重合时,△ABC才能和△APQ全等.
37.(8分)如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线.点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上.(2)若AC=5,BC=12,求OE的长.
【解】 (1)过点O作OM⊥AB于点M,连结AO.∵四边形OECF是正方形,∴OE=EC=CF=OF,OE⊥BC,OF⊥AC.又∵BD平分∠ABC,OM⊥AB,OE⊥BC,∴OM=OE,∴OM=OF.又∵AO=AO,∴Rt△AMO≌Rt△AFO(HL),∴∠MAO=∠FAO,∴点O在∠BAC的平分线上.
(2)在Rt△ABC中,∵∠C=90°,AC=5,BC=12,∴AB=13.又∵BE=BC-CE,AF=AC-CF,CE=CF=OE,∴BE=12-OE,AF=5-OE.易证BE=BM,AF=AM.∵BM+AM=AB,∴BE+AF=13,∴12-OE+5-OE=13,∴OE=2.
38..(8分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
【解】(1)证明:∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°,在Rt△ABD和Rt△ACE中,∵,∴Rt△ABD≌Rt△CAE.∴∠DAB=∠ECA,∠DBA=∠EAC.∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,∴∠BAD+∠CAE=90°.∠BAC=180°﹣(∠BAD+∠CAE)=90°.∴AB⊥AC.
(2)AB⊥AC.理由如下:同(1)一样可证得Rt△ABD≌Rt△CAE.∴∠DAB=∠ECA,∠DBA=∠EAC,∵∠CAE+∠ECA=90°,∴∠CAE+∠BAD=90°,即∠BAC=90°,∴AB⊥AC.
39.(8分)CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;EF
|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
解:(1)①∵∠BCA=90°,∠α=90°,∴∠BCE+∠CBE=90°,∠BCE+∠ACF=90°,
∴∠CBE=∠ACF,∵CA=CB,∠BEC=∠CFA;∴△BCE≌△CAF,∴BE=CF;EF=|CF﹣CE|=|BE﹣AF|.
②所填的条件是:∠α+∠BCA=180°.证明:在△BCE中,∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α.∵∠BCA=180°﹣∠α,∴∠CBE+∠BCE=∠BCA.又∵∠ACF+∠BCE=∠BCA,∴∠CBE=∠ACF,又∵BC=CA,∠BEC=∠CFA,∴△BCE≌△CAF(AAS)∴BE=CF,CE=AF,又∵EF=CF﹣CE,∴EF=|BE﹣AF|.
(2)猜想:EF=BE+AF.证明过程:∵∠BEC=∠CFA=∠α,∠α=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,∴∠BCE=∠CAF,又∵BC=CA,
∴△BCE≌△CAF(AAS).∴BE=CF,EC=FA,∴EF=EC+CF=BE+AF.
(时间:90分钟
满分:120分)
一.选择题(每小题2分
共30分)
1.
两个三角形的两条边及其中一条边的对角对应相等,则下列四个命题中,真命题的个数是(
)个①这两个三角形全等;
②相等的角为锐角时全等③相等的角为钝角对全等;
④相等的角为直角时全等
A.0
B.1
C.2
D.3
2.在下列定理中假命题是(
)
A.一个等腰三角形必能分成两个全等的直角三角形
B.一个直角三角形必能分成两个等腰三角形
C.两个全等的直角三角形必能拼成一个等腰三角形
D.两个等腰三角形必能拼成一个直角三角形
3.如图,Rt△ABC中,∠B=90°,∠ACB=60°,延长BC到D,使CD=AC则AC:BD=(
)
A.1:1
B.3:1
C.4:1
D.2:3
第3题图
第4题图
第6题图
第8题图
4.如图,在Rt△ABC中,∠ACB=90°,CD、CE,分别是斜边AB上的高与中线,CF是∠ACB的平分线.则∠1与∠2的关系是(
)
A.∠1<∠2
B.∠1=∠2;
C.∠1>∠2
D.不能确定
5.在直角三角形ABC中,若∠C=90°,D是BC边上的一点,且AD=2CD,则∠ADB的度数是(
)
A.30°
B.60°
C.120°
D.150°
6.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再取BF的垂线DE,使点A,C,E在同一条直线上(如图所示),可以证明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长.则判定△EDC≌△ABC的理由是(
)
A.
SAS
B.
ASA
C.
SSS
D.
HL
7.下列条件中,不能判定两个直角三角形全等的是(
)
A.
一条直角边和一个锐角分别相等
B.
两条直角边对应相等
C.
斜边和一条直角边对应相等
D.
斜边和一个锐角对应相等
8.如图,已知△ABC,求作一点P,使点P到∠BAC两边的距离相等,且PA=PB.下列确定点P的方法中,正确的是(
)
A.
P是∠BAC,∠ABC两角平分线的交点
B.
P为∠BAC的平分线与AB的垂直平分线的交点
C.
P为AB,AC两边上的高线的交点
D.
P为AC,AB两边的垂直平分线的交点
9.如图,直线l1,l2,l3表示相交的道路,现要选定一个货物中转站,要求该站到三条道路的距离相等,可供选择的点有(
)
A.
1处
B.
2处
C.
3处
D.
4处
第9题图
第11题图
第12题图
第14题图
10.下列说法正确的有( )
①角平分线上任意一点到角两边的距离相等;②到一个角两边的距离相等的点在这个角的平分线上;③三角形三个角平分线的交点到三个顶点的距离相等;④三角形三条角平分线的交点到三边的距离相等.
A.1个
B.2个
C.3个
D.4个
11.如图,PD⊥AB,PE⊥AC,垂足分别为D,E,且PD=PE,判定△APD与△APE全等的理由是(
)
A.SAS
B.AAS
C.SSS
D.HL
12.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是
(
)
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
13.不能使两个直角三角形全等的条件是(
)
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和两条直角边对应相等
D.两个锐角对应相等
14.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为
(
)
A.11
B.5.5
C.7
D.3.5
15.如(1)图,由已知AB⊥BD,ED⊥BD,AB=CD,BC=DE可证得AC⊥CE,若将CD沿CB方向平移到图(2)(3)(4)(5)的情形,其余条件不变,则这四种情况下,结论AC1⊥C2
E仍然成立的有(
)
A.2个
B.2个
C.3个
D.4个
二.填空题(每小题2分
共30分)
16.已知在△ABC和△A′B′C′中,∠C=∠C′=90°,要使△ABC≌△A′B′C′,可以添加条件:
_____________________________________________.
17.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌____,全等的根据是___.
第17题图
第19题图
第20题图
第21题图
18.判定两直角三角形全等的各种条件:(1)一锐角和一边对应相等(2)两边对应相等(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是____________
19.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF的度数是______,∠FBC的度数是________
20.如图,Rt△ABC中,AC=BC=6,D为AB的中点,DE⊥DF,DE,DF分别交AC、BC于点E、F.若已知DE=4,则四边形DECF的周长为______.
21.如图,在△ABC中,∠ABC=45°,F是高线AD和BE的交点,CD=4,则线段DF的长度为
22.如图,在△ABC和△ABD中,∠C=∠D=90°,若利甩“AAS”证明△ABC≌△ABD,则需要添加一个条件
或
;若利用“HL”证明:△ABC≌△ABD,则需要添加一个条件
或
.
第22题图
第23题图
第24题图
第25题图
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=
°.
24..如图,有两个长度相同的滑梯
(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=
度.
25.如图,在△ABC中,AD⊥BC于D,AD与BE相交于H,且BH=AC,DH=DC,那么∠ABC=
°.
26.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后△CAP与△PQB全等.
第26题图
第27题图
第28题图
第29题图
第30题图
27.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE=
cm.
28.如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,图中有
对全等的直角三角形.
29.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件
;
(2)若以“HL”为依据,需添加条件
.
30.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
时,△ABC和△PQA全等.
三.解答题(60分)
31.(6分)已知:如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE
求证:OB=OC.
32.(6分)已知:Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,求证:CD⊥BE
33.(6分)已知△ABC中,CD⊥AB于D,过D作DE⊥AC,F为BC中点,过F作FG⊥DC
求证:DG=EG.
34.(6分)如图,已知BN为∠ABC的平分线,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.求证:∠BAP+∠BCP=180°.
35.(6分)如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.
36.(6分)如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
37.(8分)如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线.点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上.(2)若AC=5,BC=12,求OE的长.
38..(8分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
39.(8分)CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;EF
|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
教师样卷
一.选择题(每小题2分
共30分)
1.
两个三角形的两条边及其中一条边的对角对应相等,则下列四个命题中,真命题的个数是(
C
)个①这两个三角形全等;
②相等的角为锐角时全等③相等的角为钝角对全等;
④相等的角为直角时全等
A.0
B.1
C.2
D.3
2.在下列定理中假命题是(
D
)
A.一个等腰三角形必能分成两个全等的直角三角形
B.一个直角三角形必能分成两个等腰三角形
C.两个全等的直角三角形必能拼成一个等腰三角形
D.两个等腰三角形必能拼成一个直角三角形
3.如图,Rt△ABC中,∠B=90°,∠ACB=60°,延长BC到D,使CD=AC则AC:BD=(
D
)
A.1:1
B.3:1
C.4:1
D.2:3
【解析】设BC=x则AC=2x,CD=2x
∴BD=3x∴AC:BD=2:3
第3题图
第4题图
第6题图
第8题图
4.如图,在Rt△ABC中,∠ACB=90°,CD、CE,分别是斜边AB上的高与中线,CF是∠ACB的平分线.则∠1与∠2的关系是(
B
)
A.∠1<∠2
B.∠1=∠2;
C.∠1>∠2
D.不能确定
【解析】∵CE为△ABC中线,∴AE=EC∴∠3=∠A∵CF平分∠ACB∴∠ACF=∠FCB
即∠3+∠1=∠2+∠4∵CD⊥AB,∠ACB=90°∴∠4=∠A∴∠3+∠1=∠2+∠A∴∠1=∠2
5.在直角三角形ABC中,若∠C=90°,D是BC边上的一点,且AD=2CD,则∠ADB的度数是(
C
)
A.30°
B.60°
C.120°
D.150°
【解析】∠ADC=60°∴∠ADB=120°
6.要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再取BF的垂线DE,使点A,C,E在同一条直线上(如图所示),可以证明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长.则判定△EDC≌△ABC的理由是(B)
A.
SAS
B.
ASA
C.
SSS
D.
HL
7.下列条件中,不能判定两个直角三角形全等的是(A)
A.
一条直角边和一个锐角分别相等
B.
两条直角边对应相等
C.
斜边和一条直角边对应相等
D.
斜边和一个锐角对应相等
8.如图,已知△ABC,求作一点P,使点P到∠BAC两边的距离相等,且PA=PB.下列确定点P的方法中,正确的是(B)
A.
P是∠BAC,∠ABC两角平分线的交点
B.
P为∠BAC的平分线与AB的垂直平分线的交点
C.
P为AB,AC两边上的高线的交点
D.
P为AC,AB两边的垂直平分线的交点
9.如图,直线l1,l2,l3表示相交的道路,现要选定一个货物中转站,要求该站到三条道路的距离相等,可供选择的点有(D)
A.
1处
B.
2处
C.
3处
D.
4处
【解】 如解图,作角平分线,利用角平分线上的点到角的两边的距离相等,可知P1,P2,P3,P4都满足条件.
第9题图
第11题图
第12题图
第14题图
10.下列说法正确的有( B )
①角平分线上任意一点到角两边的距离相等;②到一个角两边的距离相等的点在这个角的平分线上;③三角形三个角平分线的交点到三个顶点的距离相等;④三角形三条角平分线的交点到三边的距离相等.
A.1个
B.2个
C.3个
D.4个
11.如图,PD⊥AB,PE⊥AC,垂足分别为D,E,且PD=PE,判定△APD与△APE全等的理由是(
D
)
A.SAS
B.AAS
C.SSS
D.HL
12.如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是
(
A
)
A.AB=AC
B.∠BAC=90°
C.BD=AC
D.∠B=45°
13.不能使两个直角三角形全等的条件是(
D
)
A.一条直角边及其对角对应相等
B.斜边和一条直角边对应相等
C.斜边和两条直角边对应相等
D.两个锐角对应相等
14.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为
(
B
)
A.11
B.5.5
C.7
D.3.5
15.如(1)图,由已知AB⊥BD,ED⊥BD,AB=CD,BC=DE可证得AC⊥CE,若将CD沿CB方向平移到图(2)(3)(4)(5)的情形,其余条件不变,则这四种情况下,结论AC1⊥C2
E仍然成立的有(
D
)
A.2个
B.2个
C.3个
D.4个
二.填空题(每小题2分
共30分)
16.已知在△ABC和△A′B′C′中,∠C=∠C′=90°,要使△ABC≌△A′B′C′,可以添加条件:AC=A′C′,AB=A′B′(答案不唯一).
17.如图,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌__△DFE___,全等的根据是__HL___.
第17题图
第19题图
第20题图
第21题图
18.判定两直角三角形全等的各种条件:(1)一锐角和一边对应相等(2)两边对应相等(3)两锐角对应相等.其中能得到两个直角三角形全等的条件是(1)(2)
19.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,则∠EBF的度数是20°,∠FBC的度数是40°
20.如图,Rt△ABC中,AC=BC=6,D为AB的中点,DE⊥DF,DE,DF分别交AC、BC于点E、F.若已知DE=4,则四边形DECF的周长为14
21.如图,在△ABC中,∠ABC=45°,F是高线AD和BE的交点,CD=4,则线段DF的长度为
4
22.如图,在△ABC和△ABD中,∠C=∠D=90°,若利甩“AAS”证明△ABC≌△ABD,则需要添加一个条件
或
;若利用“HL”证明:△ABC≌△ABD,则需要添加一个条件
或
.
【答案】∠CAB=∠DAB
∠CBA=∠DBA
AC=AD
BC=BD
第22题图
第23题图
第24题图
第25题图
如图,∠AOB=70°,QC⊥OA于点C,QD⊥OB于点D,若QC=QD,则∠AOQ=
35
°.
24..如图,有两个长度相同的滑梯
(即BC=EF),左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则∠ABC+∠DFE=
90
度.
25.如图,在△ABC中,AD⊥BC于D,AD与BE相交于H,且BH=AC,DH=DC,那么∠ABC=
45
°.
26.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
4 分钟后△CAP与△PQB全等.
解:∵CA⊥AB于A,DB⊥AB于B,∴∠A=∠B=90°,设运动x分钟后△CAP与△PQB全等;则BP=xm,BQ=2xm,则AP=(12﹣x)m,分两种情况:①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,∴△CAP≌△PBQ;②若BP=AP,则12﹣x=x,解得:x=6,BQ=12≠AC,此时△CAP与△PQB不全等;综上所述:运动4分钟后△CAP与△PQB全等;故答案为:4.
第26题图
第27题图
第28题图
第29题图
第30题图
27.如图,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点B,C作过点A的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= 7
cm.
解:∵在Rt△ABC中,∠BAC=90°,∠ADB=∠AEC=90∴∠BAD+∠EAC=90°,∠BAD+∠B=90°∴∠EAC=∠B∵AB=AC∴△ABD≌△ACE(AAS)∴AD=CE,BD=AE∴DE=AD+AE=CE+BD=7cm.故填7.
28.如图,AB=AC,CD⊥AB于点D,BE⊥AC于点E,BE与CD相交于点O,图中有 3
对全等的直角三角形.
解:∵CD⊥AB,BE⊥AC,∴∠AEB=∠ADC=90°,在Rt△ABE和△Rt△ACD中
∴Rt△ABE≌△Rt△ACD(AAS),∴AD=AE,在Rt△AOD和Rt△AOE中∴Rt△AOD≌Rt△AOE(HL),∴OD=OE,在Rt△BOD和Rt△COE中
∴Rt△BOD≌Rt△COE(ASA),∴全等的直角三角形共有3对,故答案为:3.
29.如图,AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“SAS”为依据,需添加条件
AB=CD
;
(2)若以“HL”为依据,需添加条件
AD=BC
.
解:(1)若以“SAS”为依据,需添加条件:AB=CD;∵AC⊥AB,AC⊥CD,∴∠BAC=90°,∠DCA=90°,∴∠BAC=∠DCA,在△ABC和△CDA中,∵,
∴△ABC≌△CDA(SAS);
(2)若以“HL”为依据,需添加条件:AD=BC;在Rt△ABC和Rt△CDA中,
∴Rt△ABC≌Rt△CDA(HL).
30.如图,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段PQ=AB,P,Q两点分别在AC和过点A且垂直于AC的射线AO上运动,当AP=
5或10
时,△ABC和△PQA全等.
解:当AP=5或10时,△ABC和△PQA全等,理由是:∵∠C=90°,AO⊥AC,∴∠C=∠QAP=90°,①当AP=5=BC时,在Rt△ACB和Rt△QAP中∴Rt△ACB≌Rt△QAP(HL),②当AP=10=AC时,在Rt△ACB和Rt△PAQ中∴Rt△ACB≌Rt△PAQ(HL),故答案为:5或10.
三.解答题(60分)
31.(6分)已知:如图△ABC中,BD⊥AC,CE⊥AB,BD、CE交于O点,且BD=CE
求证:OB=OC.
证明:∵CE⊥AB,BD⊥AC,则∠BEC=∠CDB=90°∴在Rt△BCE与Rt△CBD中
∴Rt△BCE≌Rt△CBD(HL)∴∠1=∠2,∴OB=OC
32.(6分)已知:Rt△ABC中,∠ACB是直角,D是AB上一点,BD=BC,过D作AB的垂线交AC于E,求证:CD⊥BE
证明:∵DE⊥AB∴∠BDE=90°,∵∠ACB=90°∴在Rt△DEB中与Rt△CEB中BD=BC
BE=BE∴Rt△DEB≌Rt△CEB(HL)∴DE=EC又∵BD=BC∴E、B在CD的垂直平分线上即BE⊥CD.
33.(6分)已知△ABC中,CD⊥AB于D,过D作DE⊥AC,F为BC中点,过F作FG⊥DC
求证:DG=EG.
证明:作FQ⊥BD于Q,∴∠FQB=90°∵DE⊥AC∴∠DEC=90°∵FG⊥CD
CD⊥BD
∴BD//FG,∠BDC=∠FGC=90°∴QF//CD∴QF=DG,∴∠B=∠GFC∵F为BC中点∴BF=FC
在Rt△BQF与Rt△FGC中∴△BQF≌△FGC(AAS)∴QF=GC
∵QF=DG
∴DG=GC∴在Rt△DEC中,∵G为DC中点∴DG=EG
34.(6分)如图,已知BN为∠ABC的平分线,P为BN上一点,且PD⊥BC于点D,AB+BC=2BD.求证:∠BAP+∠BCP=180°.
【解】 过点P作PE⊥射线BA于点E.∵BN平分∠ABC,点P在BN上,PD⊥BC,PE⊥AB,∴PE=PD,∠BEP=∠BDP=90°.在Rt△PBE和Rt△PBD中,∵PB=PB,PE=PD,
∴Rt△PBE≌Rt△PBD(HL),∴BE=BD.∵AB+BC=2BD,AB=BE-AE,BC=BD+CD,
∴BE-AE+BD+CD=2BD,∴AE=CD.在△PEA和△PDC中,∵∴△PEA≌△PDC(SAS),∴∠PAE=∠PCD,即∠PAE=∠BCP.∵∠BAP+∠PAE=180°,∴∠BAP+∠BCP=180°.
35.(6分)如图,AB=AC,∠BAC=90°,BD⊥AE于D,CE⊥AE于E,且BD>CE.
求证:BD=EC+ED.
证明:∵∠BAC=90°,CE⊥AE,BD⊥AE,∴∠ABD+∠BAD=90°,∠BAD+∠DAC=90°,∠ADB=∠AEC=90°.∴∠ABD=∠DAC.∵在△ABD和△CAE中,
∴△ABD≌△CAE(AAS).∴BD=AE,EC=AD.∵AE=AD+DE,∴BD=EC+ED.
36.(6分)如图,有一直角三角形ABC,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动,问P点运动到AC上什么位置时△ABC才能和△APQ全等.
解:根据三角形全等的判定方法HL可知:①当P运动到AP=BC时,∵∠C=∠QAP=90°,在Rt△ABC与Rt△QPA中,∴Rt△ABC≌Rt△QPA(HL),即AP=BC=5cm;
②当P运动到与C点重合时,AP=AC,在Rt△ABC与Rt△QPA中,,∴Rt△QAP≌Rt△BCA(HL),即AP=AC=10cm,∴当点P与点C重合时,△ABC才能和△APQ全等.综上所述,当点P位于AC的中点处或当点P与点C重合时,△ABC才能和△APQ全等.
37.(8分)如图,在Rt△ABC中,∠C=90°,BD是△ABC的角平分线.点O,E,F分别在BD,BC,AC上,且四边形OECF是正方形.
(1)求证:点O在∠BAC的平分线上.(2)若AC=5,BC=12,求OE的长.
【解】 (1)过点O作OM⊥AB于点M,连结AO.∵四边形OECF是正方形,∴OE=EC=CF=OF,OE⊥BC,OF⊥AC.又∵BD平分∠ABC,OM⊥AB,OE⊥BC,∴OM=OE,∴OM=OF.又∵AO=AO,∴Rt△AMO≌Rt△AFO(HL),∴∠MAO=∠FAO,∴点O在∠BAC的平分线上.
(2)在Rt△ABC中,∵∠C=90°,AC=5,BC=12,∴AB=13.又∵BE=BC-CE,AF=AC-CF,CE=CF=OE,∴BE=12-OE,AF=5-OE.易证BE=BM,AF=AM.∵BM+AM=AB,∴BE+AF=13,∴12-OE+5-OE=13,∴OE=2.
38..(8分)如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
(2)若B、C在DE的两侧(如图所示),且AD=CE,其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
【解】(1)证明:∵BD⊥DE,CE⊥DE,∴∠ADB=∠AEC=90°,在Rt△ABD和Rt△ACE中,∵,∴Rt△ABD≌Rt△CAE.∴∠DAB=∠ECA,∠DBA=∠EAC.∵∠DAB+∠DBA=90°,∠EAC+∠ACE=90°,∴∠BAD+∠CAE=90°.∠BAC=180°﹣(∠BAD+∠CAE)=90°.∴AB⊥AC.
(2)AB⊥AC.理由如下:同(1)一样可证得Rt△ABD≌Rt△CAE.∴∠DAB=∠ECA,∠DBA=∠EAC,∵∠CAE+∠ECA=90°,∴∠CAE+∠BAD=90°,即∠BAC=90°,∴AB⊥AC.
39.(8分)CD经过∠BCA顶点C的一条直线,CA=CB.E,F分别是直线CD上两点,且∠BEC=∠CFA=∠α.
(1)若直线CD经过∠BCA的内部,且E,F在射线CD上,请解决下面两个问题:
①如图1,若∠BCA=90°,∠α=90°,则BE
CF;EF
|BE﹣AF|(填“>”,“<”或“=”);
②如图2,若0°<∠BCA<180°,请添加一个关于∠α与∠BCA关系的条件
,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出EF,BE,AF三条线段数量关系的合理猜想(不要求证明).
解:(1)①∵∠BCA=90°,∠α=90°,∴∠BCE+∠CBE=90°,∠BCE+∠ACF=90°,
∴∠CBE=∠ACF,∵CA=CB,∠BEC=∠CFA;∴△BCE≌△CAF,∴BE=CF;EF=|CF﹣CE|=|BE﹣AF|.
②所填的条件是:∠α+∠BCA=180°.证明:在△BCE中,∠CBE+∠BCE=180°﹣∠BEC=180°﹣∠α.∵∠BCA=180°﹣∠α,∴∠CBE+∠BCE=∠BCA.又∵∠ACF+∠BCE=∠BCA,∴∠CBE=∠ACF,又∵BC=CA,∠BEC=∠CFA,∴△BCE≌△CAF(AAS)∴BE=CF,CE=AF,又∵EF=CF﹣CE,∴EF=|BE﹣AF|.
(2)猜想:EF=BE+AF.证明过程:∵∠BEC=∠CFA=∠α,∠α=∠BCA,∠BCA+∠BCE+∠ACF=180°,∠CFA+∠CAF+∠ACF=180°,∴∠BCE=∠CAF,又∵BC=CA,
∴△BCE≌△CAF(AAS).∴BE=CF,EC=FA,∴EF=EC+CF=BE+AF.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
