2021-2022学年苏科版九年级数学上册2.1 圆(1)培优训练(word版、含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册2.1 圆(1)培优训练(word版、含答案) | 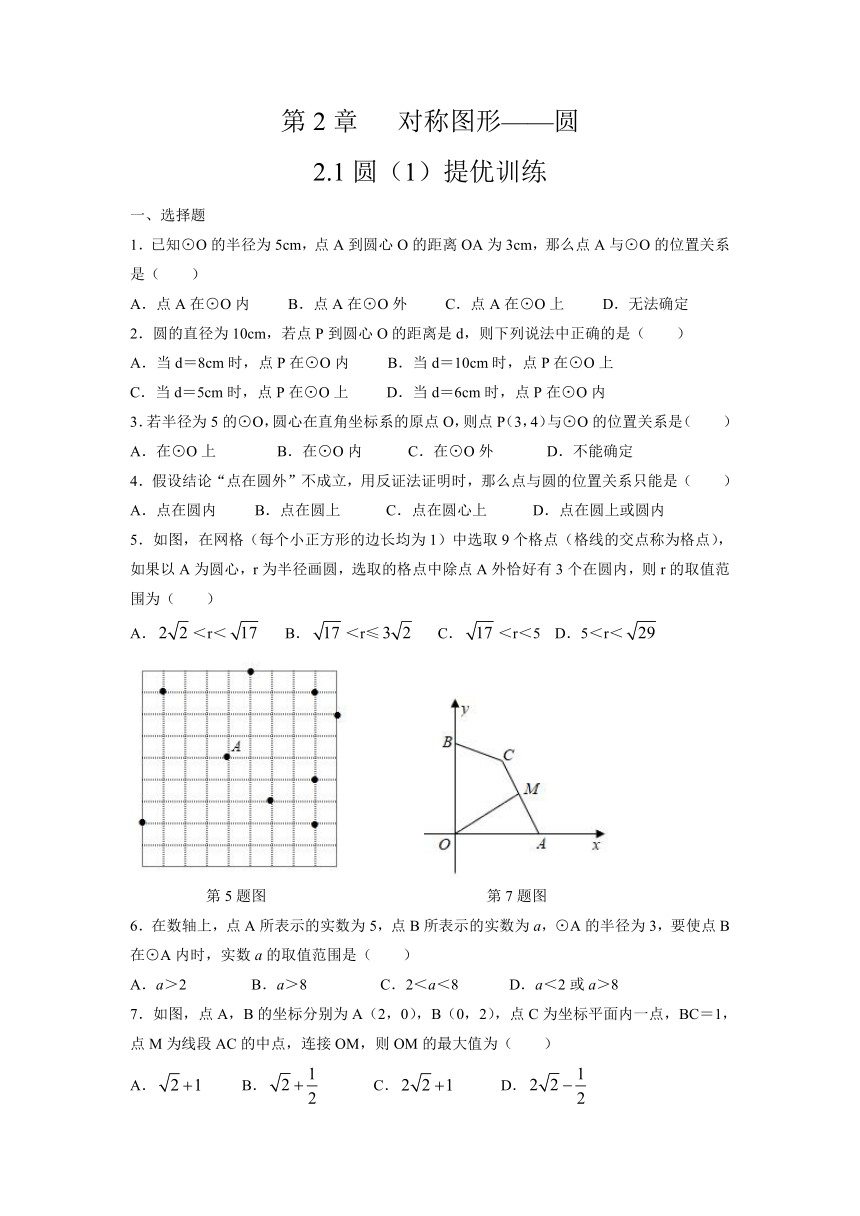 | |
| 格式 | doc | ||
| 文件大小 | 131.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 19:12:11 | ||
图片预览


文档简介
第2章
对称图形——圆
2.1圆(1)提优训练
一、选择题
1.已知⊙O的半径为5cm,点A到圆心O的距离OA为3cm,那么点A与⊙O的位置关系是(
)
A.点A在⊙O内
B.点A在⊙O外
C.点A在⊙O上
D.无法确定
2.圆的直径为10cm,若点P到圆心O的距离是d,则下列说法中正确的是(
)
A.当d=8cm时,点P在⊙O内
B.当d=10cm时,点P在⊙O上
C.当d=5cm时,点P在⊙O上
D.当d=6cm时,点P在⊙O内
3.若半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,4)与⊙O的位置关系是(
)
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.不能确定
4.假设结论“点在圆外”不成立,用反证法证明时,那么点与圆的位置关系只能是(
)
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
5.如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
A.<r<
B.<r≤
C.<r<5
D.5<r<
第5题图
第7题图
6.在数轴上,点A所表示的实数为5,点B所表示的实数为a,⊙A的半径为3,要使点B在⊙A内时,实数a的取值范围是( )
A.a>2
B.a>8
C.2<a<8
D.a<2或a>8
7.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.
B.
C.
D.
二、填空题
8.已知⊙O的半径为3,点P到圆心O的距离是关于x的一元二次方程x2-x-6=0的一根,则点P与⊙O的位置关系是
.
9.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,则经过
秒后,点P在⊙O上.
第9题图
10.若⊙O所在平面内有一点P,这一点P到⊙O上的点的最大距离为6,最小距离为2,则此圆的半径为
.
三、解答题
11.已知⊙O的半径r=10,圆心O到直线l的距离OD=6,在直线l上有A、B、C三点,AD=6,BD=8,CD=,判断A、B、C三点与⊙O的位置关系.
12.如图,已知点P、Q,且PQ=3cm.请在下列方格纸上画出图形,并用阴影部分将图形表示出来.画图要求如下:到点P的距离小于或等于2cm,且到点Q的距离小于或等于5cm的点的集合.(注:方格纸中每格长度代表1cm,不要求写法.)
13.如图,在四边形ABCD中,∠ABC,∠ADC均为直角,且AB=3,BC=4,AD=2.
(1)求证:A,B,C,D四个点都在同一个圆上;
(2)求这个圆的半径,并计算它的面积.
14.在△ABC中,∠C=90°,AC=4cm,BC=3cm,以点C为圆心,为半径作⊙C.
(1)若A,B两点都不在⊙C内,求半径r的取值范围;
(2)若A,B两点都在⊙C内,求半径r的取值范围;
(3)若A,B两点中只有一个点在⊙C内,求半径r的取值范围.
15.如图,矩形纸片ABCD一边BC过圆心O,且AB=4cm,BE=3cm,AF=5cm,求圆的半径.
参考答案
一、选择题
1—7
ACADBCB
二、填空题
8.点在圆上
9.2或
10.2或4
三、解答题
11.由题意,得
因为⊙O的半径
所以点在⊙O内,点在⊙O上,点在⊙O外.
12.解:如下图所示
13.(1)取直角三角形ABC斜边AC的中点E,连接BE、DE.
因为均为直角,
所以和均为直角三角形,
所以
所以A,B,C,D四个点都在以E为圆心的同一个圆上.
(2)在Rt△ABC中,,
所以该圆的半径,.
14.()因为A,B两点都不在⊙C内,所以半径r小于BC,所以0
cm<r≤3
cm
(2)因为A,B两点都在⊙C内,所以半径r大于AC,所以r>4cm
(3)因为A,B两点中只有一个点在⊙C内,所以半径r大于BC且小于AC,所以3
cm<r≤4
cm
15.过点F作FH⊥BC,垂足为H,连接OF,则AF=BH=5cm,AB=FH=4cm
因为BE=3cm,所以EH=2cm
设圆的半径为r
cm,则OF=r
cm,OH=(r—2)cm
在Rt△OFH中,,解得r=5
故圆的半径为5cm.
l
对称图形——圆
2.1圆(1)提优训练
一、选择题
1.已知⊙O的半径为5cm,点A到圆心O的距离OA为3cm,那么点A与⊙O的位置关系是(
)
A.点A在⊙O内
B.点A在⊙O外
C.点A在⊙O上
D.无法确定
2.圆的直径为10cm,若点P到圆心O的距离是d,则下列说法中正确的是(
)
A.当d=8cm时,点P在⊙O内
B.当d=10cm时,点P在⊙O上
C.当d=5cm时,点P在⊙O上
D.当d=6cm时,点P在⊙O内
3.若半径为5的⊙O,圆心在直角坐标系的原点O,则点P(3,4)与⊙O的位置关系是(
)
A.在⊙O上
B.在⊙O内
C.在⊙O外
D.不能确定
4.假设结论“点在圆外”不成立,用反证法证明时,那么点与圆的位置关系只能是(
)
A.点在圆内
B.点在圆上
C.点在圆心上
D.点在圆上或圆内
5.如图,在网格(每个小正方形的边长均为1)中选取9个格点(格线的交点称为格点),如果以A为圆心,r为半径画圆,选取的格点中除点A外恰好有3个在圆内,则r的取值范围为( )
A.<r<
B.<r≤
C.<r<5
D.5<r<
第5题图
第7题图
6.在数轴上,点A所表示的实数为5,点B所表示的实数为a,⊙A的半径为3,要使点B在⊙A内时,实数a的取值范围是( )
A.a>2
B.a>8
C.2<a<8
D.a<2或a>8
7.如图,点A,B的坐标分别为A(2,0),B(0,2),点C为坐标平面内一点,BC=1,点M为线段AC的中点,连接OM,则OM的最大值为( )
A.
B.
C.
D.
二、填空题
8.已知⊙O的半径为3,点P到圆心O的距离是关于x的一元二次方程x2-x-6=0的一根,则点P与⊙O的位置关系是
.
9.如图,数轴上半径为1的⊙O从原点O开始以每秒1个单位的速度向右运动,同时,距原点右边7个单位有一点P以每秒2个单位的速度向左运动,则经过
秒后,点P在⊙O上.
第9题图
10.若⊙O所在平面内有一点P,这一点P到⊙O上的点的最大距离为6,最小距离为2,则此圆的半径为
.
三、解答题
11.已知⊙O的半径r=10,圆心O到直线l的距离OD=6,在直线l上有A、B、C三点,AD=6,BD=8,CD=,判断A、B、C三点与⊙O的位置关系.
12.如图,已知点P、Q,且PQ=3cm.请在下列方格纸上画出图形,并用阴影部分将图形表示出来.画图要求如下:到点P的距离小于或等于2cm,且到点Q的距离小于或等于5cm的点的集合.(注:方格纸中每格长度代表1cm,不要求写法.)
13.如图,在四边形ABCD中,∠ABC,∠ADC均为直角,且AB=3,BC=4,AD=2.
(1)求证:A,B,C,D四个点都在同一个圆上;
(2)求这个圆的半径,并计算它的面积.
14.在△ABC中,∠C=90°,AC=4cm,BC=3cm,以点C为圆心,为半径作⊙C.
(1)若A,B两点都不在⊙C内,求半径r的取值范围;
(2)若A,B两点都在⊙C内,求半径r的取值范围;
(3)若A,B两点中只有一个点在⊙C内,求半径r的取值范围.
15.如图,矩形纸片ABCD一边BC过圆心O,且AB=4cm,BE=3cm,AF=5cm,求圆的半径.
参考答案
一、选择题
1—7
ACADBCB
二、填空题
8.点在圆上
9.2或
10.2或4
三、解答题
11.由题意,得
因为⊙O的半径
所以点在⊙O内,点在⊙O上,点在⊙O外.
12.解:如下图所示
13.(1)取直角三角形ABC斜边AC的中点E,连接BE、DE.
因为均为直角,
所以和均为直角三角形,
所以
所以A,B,C,D四个点都在以E为圆心的同一个圆上.
(2)在Rt△ABC中,,
所以该圆的半径,.
14.()因为A,B两点都不在⊙C内,所以半径r小于BC,所以0
cm<r≤3
cm
(2)因为A,B两点都在⊙C内,所以半径r大于AC,所以r>4cm
(3)因为A,B两点中只有一个点在⊙C内,所以半径r大于BC且小于AC,所以3
cm<r≤4
cm
15.过点F作FH⊥BC,垂足为H,连接OF,则AF=BH=5cm,AB=FH=4cm
因为BE=3cm,所以EH=2cm
设圆的半径为r
cm,则OF=r
cm,OH=(r—2)cm
在Rt△OFH中,,解得r=5
故圆的半径为5cm.
l
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
