2021-2022学年苏科版八年级数学上册第一章全等三角形阶段培优练习题(练习范围1.3--SAS、ASA、AAS、SSS)(word版、含解析)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册第一章全等三角形阶段培优练习题(练习范围1.3--SAS、ASA、AAS、SSS)(word版、含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 00:00:00 | ||
图片预览


文档简介
第一章
阶段培优练习题(练习范围1.3--SAS、ASA、AAS、SSS)
2021-2022学年苏科版八年级数学上册
一、选择题
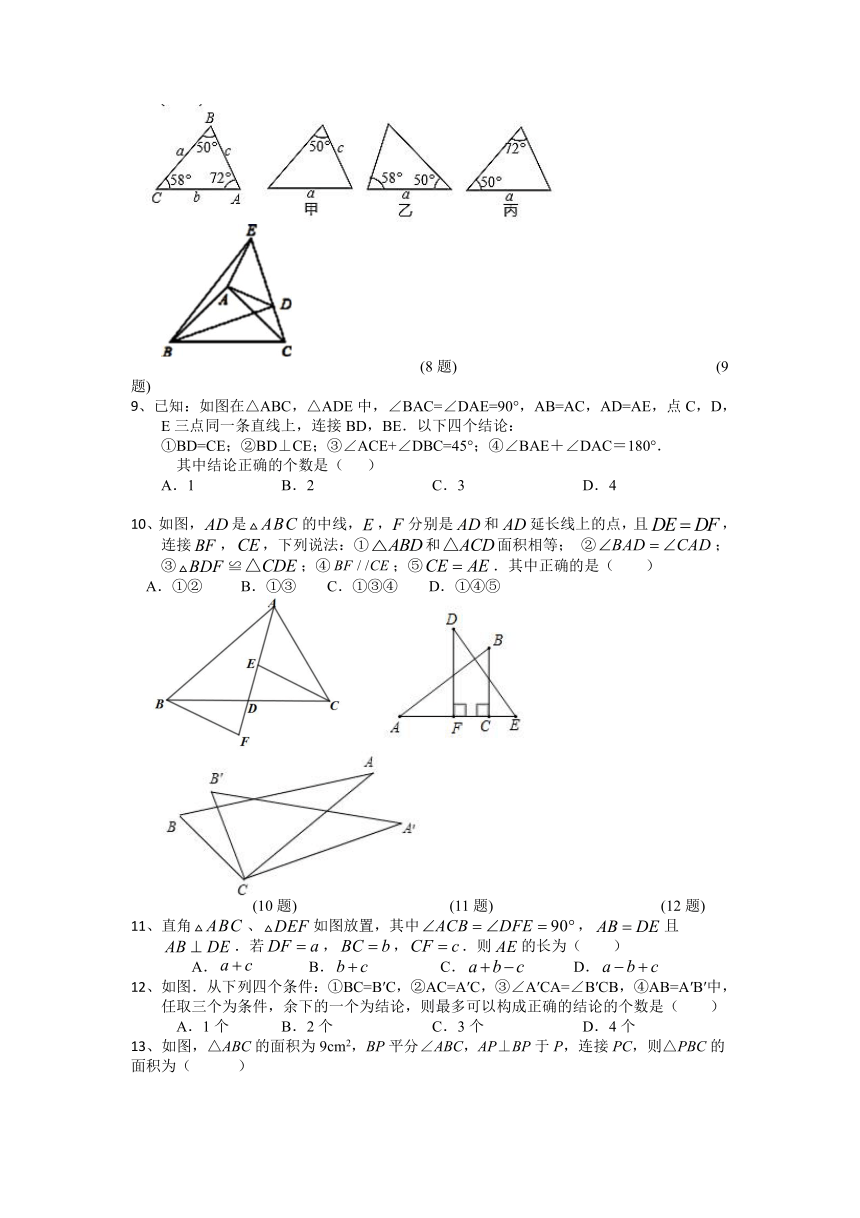
1、根据下列已知条件,能画出唯一的△ABC的是(
)
A.,,
B.,,
C.,
D.,,
2、如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE;可利用的是(
)
A.①或②
B.②或③
C.③或①
D.①或④
(2题)
(3题)
(4题)
3、如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是(
)
A.∠B=∠E,BC=EF
B.∠A=∠D,BC=EF
C.∠A=∠D,∠B=∠E
D.BC=EF,AC=DF
4、如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
5、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=60°,∠B=25°,则∠EOB的度数为(
)
A.60°
B.70°
C.75°
D.85°
(5题)
(6题)
(7题)
6、如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6
B.0.8
C.1
D.1.6
7、如图,在△ABC中,∠A=50°,∠B=∠C,点D,E,F分别在边BC,CA,AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为( )
A.75°
B.80°
C.65°
D.95°
8、如图,已知△的六个元素,则下面甲、乙、丙三个三角形和△全等的图是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
(8题)
(9题)
9、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠BAE+∠DAC=180°.
其中结论正确的个数是(
)
A.1
B.2
C.3
D.4
10、如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和面积相等;
②;
③≌;④;⑤.其中正确的是(
)
A.①②
B.①③
C.①③④
D.①④⑤
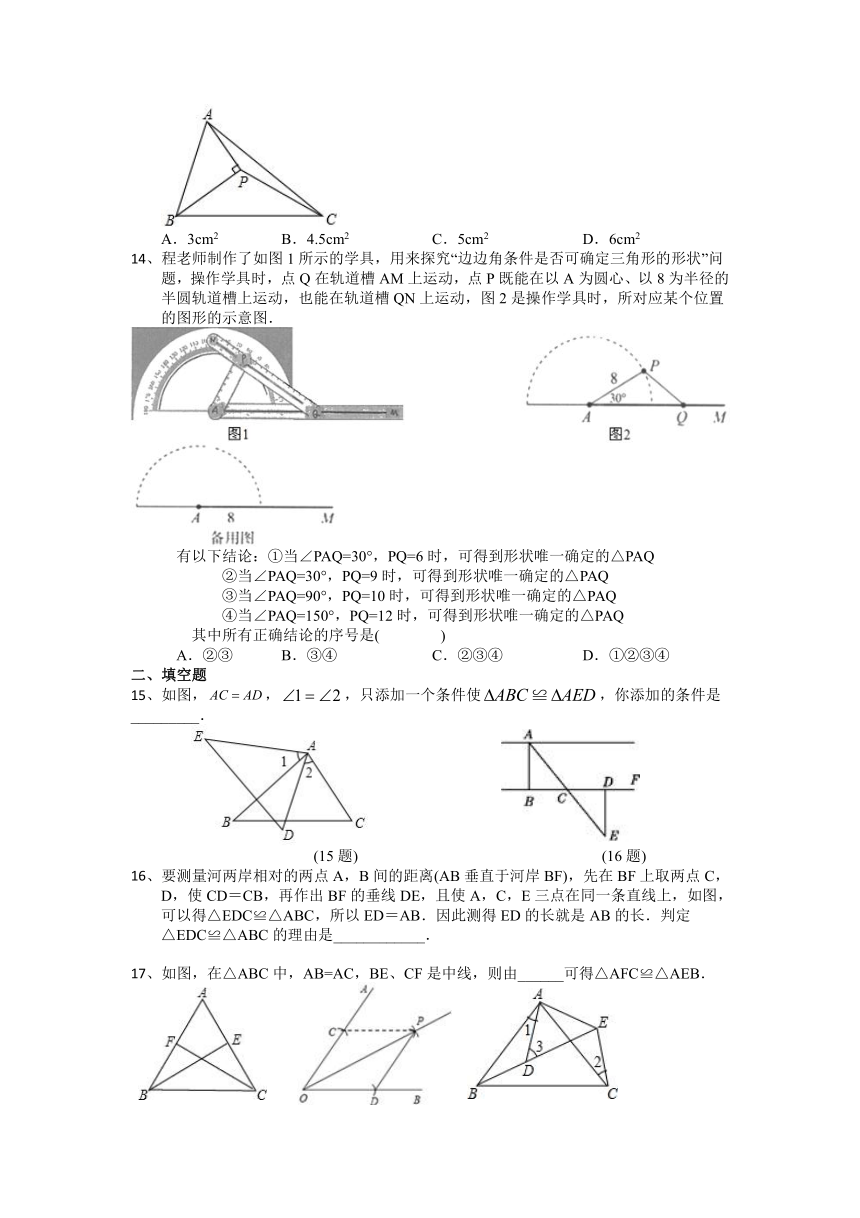
(10题)
(11题)
(12题)
11、直角、如图放置,其中,且.若,,.则的长为(
)
A.
B.
C.
D.
12、如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
13、如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4.5cm2
C.5cm2
D.6cm2
14、程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
其中所有正确结论的序号是(
)
A.②③
B.③④
C.②③④
D.①②③④
二、填空题
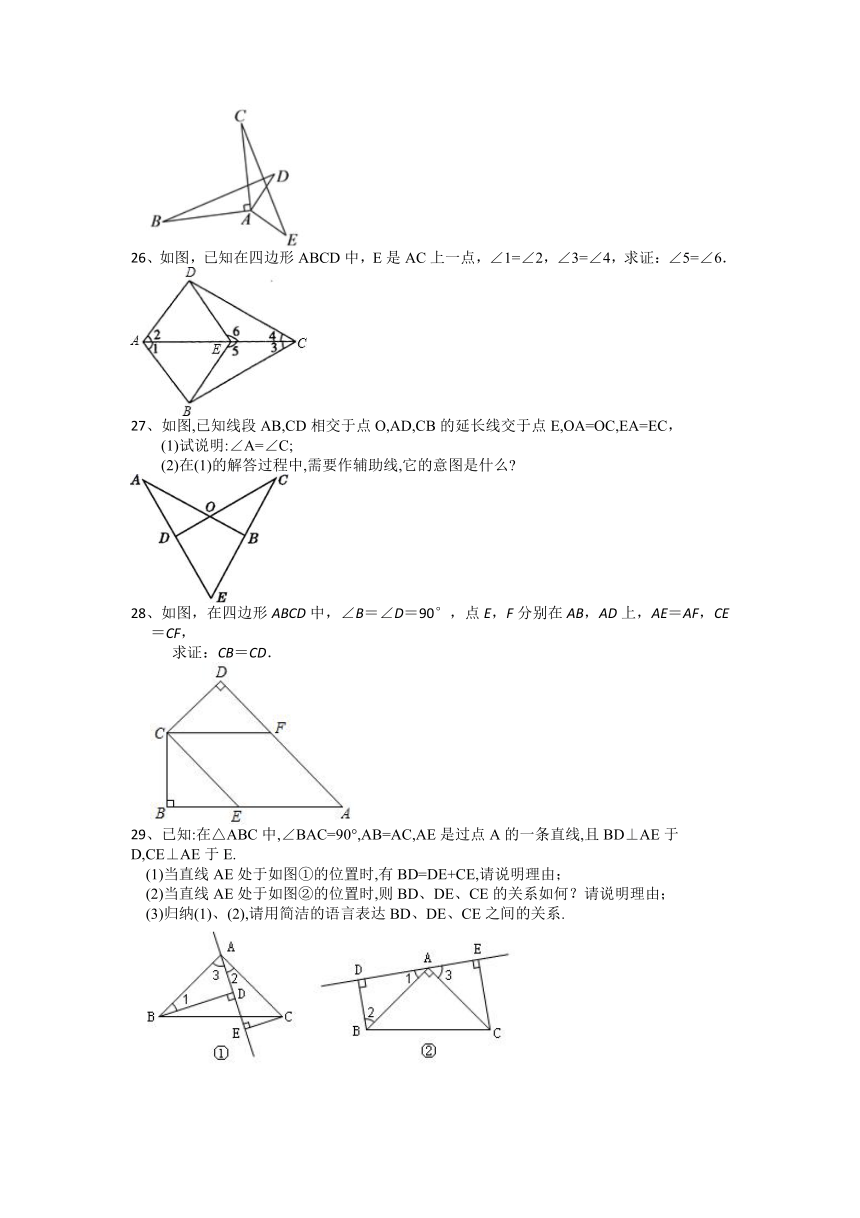
15、如图,,,只添加一个条件使,你添加的条件是_________.
(15题)
(16题)
16、要测量河两岸相对的两点A,B间的距离(AB垂直于河岸BF),先在BF上取两点C,D,使CD=CB,再作出BF的垂线DE,且使A,C,E三点在同一条直线上,如图,可以得△EDC≌△ABC,所以ED=AB.因此测得ED的长就是AB的长.判定△EDC≌△ABC的理由是____________.
17、如图,在△ABC中,AB=AC,BE、CF是中线,则由______可得△AFC≌△AEB.
(17题)
(18题)
(19题)
(20题)
18、尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP.
由作法得△OCP≌△ODP的根据是_________.
19、如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
20、如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是__________
21、如图,在Rt△ABC中,∠ABC=90°,BC=5,BD⊥AC于点D,点E在边AB上,且BE=BC,过点E作EF⊥AB交BD延长线于点F,若EF=12,则AE=_____.
(21题)
(22题)
(23题)
(24题)
22、如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
23、已知中,,,点为的中点,点、分别为边、上的动点,且,连接,下列说法正确的是______.(写出所有正确结论的序号)
①;②;③;④
24、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E、作QF⊥l于F,当点P运动
秒时,以P、E、C为顶点的三角形和以Q、F、C为顶点的三角形全等.
三、解答题
25、如图,已知,,,,
试猜想与的位置关系并说明理由.
26、如图,已知在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4,求证:∠5=∠6.
27、如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC,
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
28、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,
求证:CB=CD.
29、已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
30、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE为多少?说明理由;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?
请直接写出你的结论,不需证明.
第一章
阶段培优练习题(练习范围1.3--SAS、ASA、AAS、SSS)
2021-2022学年苏科版八年级数学上册
一、选择题
1、根据下列已知条件,能画出唯一的△ABC的是(
)
A.,,
B.,,
C.,
D.,,
【答案】B
【解析】A、不符合三角形三边之间的关系,不能作出三角形,错误;
B、符合全等三角形判定中的SSS,正确;
C、只有两个条件,不足以构成三角形,错误;
D、三个角不能画出唯一的三角形,错误,
故选B.
2、如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE;可利用的是(
)
A.①或②
B.②或③
C.③或①
D.①或④
【答案】A
【解析】
试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
3、如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是(
)
A.∠B=∠E,BC=EF
B.∠A=∠D,BC=EF
C.∠A=∠D,∠B=∠E
D.BC=EF,AC=DF
【答案】B
【分析】根据全等三角形的判定定理对选项逐一进行判断即可.
【详解】添加∠B=∠E,BC=EF可用SAS判定两个三角形全等,故A选项不符合题意,
添加∠A=∠D,BC=EF是SSA,不能判定两个三角形全等,故B选项符合题意,
添加∠A=∠D,∠B=∠E可用ASA判定两个三角形全等,故C选项不符合题意,
添加BC=EF,AC=DF可用SSS判定两个三角形全等,故D选项不符合题意.
故选B.
4、如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
【答案】B
【解析】
试题分析:∵AE=CF,∴AE+EF=CF+EF.∴AF=CE.
A.∵在△ADF和△CBE中,,∴△ADF≌△CBE(ASA),正确,故本选项错误.
B.根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确.
C.∵在△ADF和△CBE中,,∴△ADF≌△CBE(SAS),正确,故本选项错误.
D.∵AD∥BC,∴∠A=∠C.由A选项可知,△ADF≌△CBE(ASA),正确,故本选项错误.
故选B.
5、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=60°,∠B=25°,则∠EOB的度数为(
)
A.60°
B.70°
C.75°
D.85°
【答案】B
【解析】
试题解析:
故选B.
6、如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6
B.0.8
C.1
D.1.6
【分析】根据AAS证明△DBF与△ABC全等,利用全等三角形的性质解答即可.
【解析】∵DE⊥AC于E,∴∠FDB+∠C=90°,
∵∠ABC=90°,∴∠D+∠DFB=90°,∴∠C=∠BFD,
在△DBF与△ABC中,
∴△DBF≌△ABC(AAS),∴BF=BC,
∵DC=2.6,BF=1,
∴AF=AB﹣BF=BD﹣BF=DC﹣BF﹣BF=2.6﹣1﹣1=0.6,
故选:A.
7、如图,在△ABC中,∠A=50°,∠B=∠C,点D,E,F分别在边BC,CA,AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为( )
A.75°
B.80°
C.65°
D.95°
【分析】由∠B=∠C,∠A=50°,利用三角形内角和为180°得∠B=65°,∠FDB=85°,再由BF=CD,BD=CE,利用SAS得到△BDF≌△CED,利用全等三角形对应角相等得到∠BFD=∠CDE,利用三角形内角和即可得证.
【解析】∵∠B=∠C,∠A=50°,∴∠B=∠C=×(180°﹣50°)=65°,
∵∠BFD=30°,∠BFD+∠B+∠FDB=180°,
∴∠FDB=85°
在△BDF和△CED中,
∴△BDF≌△CED(SAS),∴∠BFD=∠CDE=30°,
又∵∠FDE+∠FDB+∠CDE=180°,
∴∠FDE=180°﹣30°﹣85°=65°.
故选:C.
8、如图,已知△的六个元素,则下面甲、乙、丙三个三角形和△全等的图是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
【答案】B
【分析】根据全等三角形的判定方法进行逐个验证,做题时要找准对应边,对应角.
【详解】解:如图:
图甲不符合三角形全等的判定定理,即图甲和不全等;
在和中,?∴,
图乙符合定理,即图乙和全等;
在和中,∴,
图丙符合定理,即图丙和全等.
甲、乙、丙三个三角形中和全等的图形是:乙或丙.
故选:.
9、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠BAE+∠DAC=180°.
其中结论正确的个数是(
)
A.1
B.2
C.3
D.4
【答案】D
【分析】①由AB=AC,AD=AE,利用等式的性质得到夹角相等,利用SAS得出△ABD≌△ACE,由全等三角形的对应边相等得到BD=CE;
②由△ABD≌△ACE得到一对角相等,再利用等腰直角三角形的性质及等量代换得到BD垂直于CE;
③由等腰直角三角形的性质得到∠ABD+∠DBC=45°,等量代换得到∠ACE+∠DBC=45°;
④由题意,∠BAE+∠DAC=360°-∠BAC-∠DAE=180°.
【详解】
解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE,本选项正确;
②∵△BAD≌△CAE,∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD⊥CE,本选项正确;
③∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ABD+∠DBC=45°,
∵∠ABD=∠ACE,
∴∠ACE+∠DBC=45°,本选项正确;
④由题意,∠BAE+∠DAC=360°-∠BAC-∠DAE=360°-90°-90°=180°,本选项正确;
故选D.
10、如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和面积相等;
②;
③≌;④;⑤.其中正确的是(
)
A.①②
B.①③
C.①③④
D.①④⑤
【答案】C
【分析】根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE.
【详解】解:∵AD是△ABC的中线,∴BD=CD,∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,,∴△BDF≌△CDE(SAS),故③正确;
∴∠F=∠DEC,∴BF∥CE,故④正确;
∵△BDF≌△CDE,∴CE=BF,故⑤错误,
正确的结论为:①③④,
故选:C.
11、直角、如图放置,其中,且.若,,.则的长为(
)
A.
B.
C.
D.
【答案】C
【分析】先利用AAS证明,再根据全等三角形的性质进行线段和差计算即可.
【详解】解:,,,,,
在与中,;
,,
∵,,,,∴
故选C.
12、如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【分析】将条件进行组合后,利用三角形全等的判定进行判断即可.
【详解】①②③为条件,根据SAS,可判定;可得结论④;
①②④为条件,根据SSS,可判定;可得结论③;
①③④为条件,SSA不能证明,
②③④为条件,SSA不能证明,
最多可以构成正确结论2个,故选B.
13、如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4.5cm2
C.5cm2
D.6cm2
【答案】B
【分析】根据已知条件证得△ABP≌△EBP,根据全等三角形的性质得到AP=PE,得出S△ABP=S△EBP,S△ACP=S△ECP,推出S△PBC=S△ABC,代入求出即可.
【详解】解:延长AP交BC于E,
∵BP平分∠ABC,∴∠ABP=∠EBP,
∵AP⊥BP,∴∠APB=∠EPB=90°,
在△ABP和△EBP中,,∴△ABP≌△EBP(ASA),
∴AP=PE,∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×9cm2=4.5cm2,
故选:B.
14、程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
其中所有正确结论的序号是(
)
A.②③
B.③④
C.②③④
D.①②③④
【答案】C
【分析】分别在以上四种情况下以P为圆心,PQ的长度为半径画弧,观察弧与直线AM的交点即为Q点,作出后可得答案.
【详解】如下图,当∠PAQ=30°,PQ=6时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现两个位置的Q都符合题意,所以不唯一,所以①错误.
如下图,当∠PAQ=30°,PQ=9时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现左边位置的Q不符合题意,所以唯一,所以②正确.
如下图,当∠PAQ=90°,PQ=10时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现两个位置的Q都符合题意,但是此时两个三角形全等,所以形状相同,所以唯一,所以③正确.
如下图,当∠PAQ=150°,PQ=12时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现左边位置的Q不符合题意,所以唯一,所以④正确.
综上:②③④正确.
故选C.
二、填空题
15、如图,,,只添加一个条件使,你添加的条件是_________.
【答案】∠C=∠D或∠B=∠E或AB=AE
【分析】由已知∠1=∠2可得∠BAC=∠EAD,又有AC=AD,还缺少边或角对应相等的条件,结合判定方法及图形进行选择即可.可根据判定定理ASA、SAS尝试添加条件.
【详解】(1)添加∠C=∠D.
∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,∴∠CAB=∠DAE,
在△ABC与△AED中,,∴△ABC≌△AED(ASA);
(2)添加∠B=∠E.
∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,
∴∠CAB=∠DAE,
在△ABC与△AED中,,∴△ABC≌△AED(AAS);
(3)添加AB=AE,
∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,∴∠CAB=∠DAE,
在△ABC与△AED中,,∴△ABC≌△AED(SAS),
故答案为:∠C=∠D或∠B=∠E或AB=AE.
16、要测量河两岸相对的两点A,B间的距离(AB垂直于河岸BF),先在BF上取两点C,D,使CD=CB,再作出BF的垂线DE,且使A,C,E三点在同一条直线上,如图,可以得△EDC≌△ABC,所以ED=AB.因此测得ED的长就是AB的长.判定△EDC≌△ABC的理由是____________.
【答案】ASA
【分析】由已知可以得到∠ABC=∠BDE=90°,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC.
【详解】∵BF⊥AB,DE⊥BD,∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE,∴△EDC≌△ABC(ASA)
故答案为ASA
17、如图,在△ABC中,AB=AC,BE、CF是中线,则由______可得△AFC≌△AEB.
【答案】:SAS.
【解析】
【分析】由AB=AC,BE、CF是中线可知AE=AF,由∠A是公共角,AB=AC即可根据SAS证明△AFC≌△AEB.
【详解】∵BE、CF是中线,∴AF=AB,AE=AC,
∵AB=AC∴AE=AF,
∵AE=AF,∠A=∠A,AB=AC,∴△AFC≌△AEB(SAS).
故答案为SAS
18、尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP.
由作法得△OCP≌△ODP的根据是_________.
【答案】SSS
【解析】
解:∵以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD.以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP.在△OCP和△ODP中,∵OC=OD,OP=OP,CP=DP,∴△OCP≌△ODP(SSS).故答案为SSS.
19、如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
【分析】求出∠BAD=∠EAC,证△BAD≌△CAE,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解析】∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴∠2=∠ABD=30°,
∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
20、如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是__________
【答案】2<AD<4
【分析】此题要倍长中线,再连接,构造全等三角形.根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
【详解】
解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,∴BD=CD,
在△ADC与△EDB中,∴△ADC≌△EDB(SAS),∴EB=AC,
根据三角形的三边关系定理:6-2<AE<6+2,
∴2<AD<4,
故AD的取值范围为2<AD<4.
21、如图,在Rt△ABC中,∠ABC=90°,BC=5,BD⊥AC于点D,点E在边AB上,且BE=BC,过点E作EF⊥AB交BD延长线于点F,若EF=12,则AE=_____.
【答案】7
【分析】由题意知:BD⊥AC,EF⊥AB,∠ADB=∠FEB=90°,∠A=∠F,△ABC≌△FEB(AAS),
AB=EF=12,AE=7.
【详解】解:∵BD⊥AC,EF⊥AB,∴∠ADB=∠FEB=90°,
∴∠A+∠ABD=∠F+∠FBE=90°,∴∠A=∠F,
在△ABC和△FEB中,
,∴△ABC≌△FEB(AAS),
∴AB=EF=12,
∵BE=BC=5,∴AE=AB﹣BE=7.
故填:7.
22、如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
【答案】①②③
【分析】∠E=∠F=90°,∠B=∠C,AE=AF可得△ABE≌△ACF,三角形全等的性质BE=CF;∠BAE=∠CAF可得①∠1=∠2;由ASA可得△ACN≌△ABM.④CD=DN不成立.
【详解】解:∵∠E=∠F=90°,∠B=∠C,AE=AF,∴△ABE≌△ACF,
∴BE=CF,
∠BAE=∠CAF
∠BAE-∠BAC=∠CAF-∠BAC,
∴∠1=∠2
△ABE≌△ACF,
∴∠B=∠C,AB=AC
又∠BAC=∠CAB,
△ACN≌△ABM.
④CD=DN不能证明成立,3个结论对.
故答案是:①②③
23、已知中,,,点为的中点,点、分别为边、上的动点,且,连接,下列说法正确的是______.(写出所有正确结论的序号)
①;②;③;④
【答案】①②④
【分析】
根据补角的性质计算可得①;连接D,证明,根据三角形全等的性质判断可得后面的结果;
【详解】,
,
,
;故①正确;
连接AD,
∵,,∴,
又∵点为的中点,
∴,,,即,
又∵,∴,
又∵,∴,
在△BED和△AFD中,,∴,∴ED=FD;故②正确;
∵,∴,
则,故④正确;
当点E移动到点A时,此时点F与点C重合,很明显此时EF=AC,FC=0,即;故③错误;
故答案为①②④.
24、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E、作QF⊥l于F,当点P运动
秒时,以P、E、C为顶点的三角形和以Q、F、C为顶点的三角形全等.
【解题思路】根据题意分为五种情况,根据全等三角形的性质得出CP=CQ,代入得出关于t的方程,解方程即可.
【解答过程】解:分为五种情况:
①如图1,P在AC上,Q在BC上,则PC=6﹣t,QC=8﹣3t,
∵PE⊥l,QF⊥l,∴∠PEC=∠QFC=90°,
∵∠ACB=90°,∴∠EPC+∠PCE=90°,∠PCE+∠QCF=90°,∴∠EPC=∠QCF,
∵△PCE≌△CQF,∴PC=CQ,即6﹣t=8﹣3t,t=1;
②如图2,P在BC上,Q在AC上,则PC=t﹣6,QC=3t﹣8,
∵由①知:PC=CQ,∴t﹣6=3t﹣8,t=1;t﹣6<0,即此种情况不符合题意;
③当P、Q都在AC上时,如图3,CP=6﹣t=3t﹣8,t=;
④当Q到A点停止,P在BC上时,AC=PC,t﹣6=6时,解得t=12.
⑤P和Q都在BC上的情况不存在,因为P的速度是每秒1cm,Q的速度是每秒3cm;
答:点P运动1或或12秒时,以P、E、C为顶点的三角形上以O、F、C为顶点的三角形全等.
故答案为:1或或12.
三、解答题
25、如图,已知,,,,
试猜想与的位置关系并说明理由.
【答案】.理由见解析
【解析】
试题分析:根据SSS证明△ABD≌△ACE,从而得∠BAD=∠CAE,再由∠CAD是公共角,从而可得∠DAE=∠BAC=90°,从而得到AD⊥AE.
试题解析:∵AB⊥AC,∴∠BAC=90°,
在△ABD和△ACE中,∴△ABD≌△ACE(SSS),∴∠BAD=∠CAE,
∴∠BAD-∠CAD=∠CAE-∠CAD,
即∠DAE=∠BAC=90°,
∴AD⊥AE.
26、如图,已知在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4,求证:∠5=∠6.
【答案】证明见解析
【分析】因为∠1=∠2,∠3=∠4,AC=CA,根据ASA易证△ADC≌△ABC,所以有DC=BC,又因为∠3=∠4,EC=CE,则可根据SAS判定△CED≌△CEB,故∠5=∠6.
【详解】
证明:∵,∴△ADC≌△ABC(ASA).∴DC=BC.
又∵,∴△CED≌△CEB(SAS).∴∠5=∠6.
27、如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC,
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
【答案】(1)见解析;(2)构造全等三角形.
【分析】(1)根据题意,没有证明两三角形全等的条件,所以要作条辅助线,连接OE;然后就可以利用SSS全等判定定理证明两三角形全等,继而∠A=∠C,本题即可证明;
(2)说明OE的意义即可.
【详解】(1)如图,连接OE.
在△EAO和△ECO中,,所以△EAO≌△ECO(SSS).
所以∠A=∠C(全等三角形的对应角相等).
(2)
在(1)的解答过程中,需要作辅助线,它的意图是构造全等三角形.
28、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,
求证:CB=CD.
【分析】连接AC,先利用SSS证明△ACE≌△ACF,可得∠EAC=∠FAC,再利用AAS证明△ACB≌△ACD即可得结论.
【解答】证明:如图,连接AC,
在△ACE和△ACF中,
∴△ACE≌△ACF(SSS),∴∠EAC=∠FAC,
在△ACB和△ACD中,
∴△ACB≌△ACD(AAS),∴CB=CD.
29、已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
【答案】(1)见解析
(2)见解析
(3)BD=DE-CE
【解析】此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,利用了转化及等量代换的思想,熟练掌握全等三角形的判定与性质是解本题的关键.
(1)由BD垂直于AE,得到三角形ABD为直角三角形,利用直角三角形两锐角互余得到一对角互余,再由∠BAC=90°,得到一对角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,AB=AC,利用AAS可得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=AD+DE,等量代换即可得证;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系为BD=DE-CE,理由为:同(1)得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=DE-AD等量代换即可得证;
(3)由(1)(2)总结得到当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.
解:(1)证明:∵BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°,∴∠ABD+∠BAD=90°,
∵∠BAC=90°,∴∠BAD+∠EAC=90°,∴∠ABD=∠EAC,
在△ABD和△CAE中∵
∴△ABD≌△CAE(AAS),∴AD=CE,BD=AE,
∵AE=AD+DE,∴BD=DE+CE;
(2)BD、DE、CE的关系为BD=DE-CE,理由为:
证明:在△ABD和△CAE中
△ABD≌△CAE(AAS),∴AD=CE,BD=AE,
∵AE=DE-AD,∴BD=DE-CE;
(3)当D、E位于直线BC异侧时,BD=DE+CE;
当D、E位于直线BC同侧时,BD=DE-CE.
30、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE为多少?说明理由;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?
请直接写出你的结论,不需证明.
【答案】(1)90°;(2)①α+β=180°,理由见详解;②点D在直线BC上移动,α+β=180°或α=β.
【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD≌△CAE,可得∠ABC=∠ACE=45°,可求∠BCE的度数;
(2)①由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论;②分两种情况画出图形,由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论.
【详解】解:(1)∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,
∵∠DAE=∠BAC,∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△BAD≌△CAE(SAS)
∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°;
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,∴∠BAC?∠DAC=∠DAE?∠DAC.即∠BAD=∠CAE.
在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,∴α+β=180°;
②如图1:当点D在射线BC上时,α+β=180°,
连接CE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°,
即:∠BCE+∠BAC=180°,∴α+β=180°,
如图2:当点D在射线BC的反向延长线上时,α=β.
连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,
∴∠ABD=∠ACE=∠ACB+∠BCE,
∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,
∵∠BAC=180°?∠ABC?∠ACB,∴∠BAC=∠BCE.∴α=β;
综上所述:点D在直线BC上移动,α+β=180°或α=β.
阶段培优练习题(练习范围1.3--SAS、ASA、AAS、SSS)
2021-2022学年苏科版八年级数学上册
一、选择题
1、根据下列已知条件,能画出唯一的△ABC的是(
)
A.,,
B.,,
C.,
D.,,
2、如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE;可利用的是(
)
A.①或②
B.②或③
C.③或①
D.①或④
(2题)
(3题)
(4题)
3、如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是(
)
A.∠B=∠E,BC=EF
B.∠A=∠D,BC=EF
C.∠A=∠D,∠B=∠E
D.BC=EF,AC=DF
4、如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
5、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=60°,∠B=25°,则∠EOB的度数为(
)
A.60°
B.70°
C.75°
D.85°
(5题)
(6题)
(7题)
6、如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6
B.0.8
C.1
D.1.6
7、如图,在△ABC中,∠A=50°,∠B=∠C,点D,E,F分别在边BC,CA,AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为( )
A.75°
B.80°
C.65°
D.95°
8、如图,已知△的六个元素,则下面甲、乙、丙三个三角形和△全等的图是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
(8题)
(9题)
9、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠BAE+∠DAC=180°.
其中结论正确的个数是(
)
A.1
B.2
C.3
D.4
10、如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和面积相等;
②;
③≌;④;⑤.其中正确的是(
)
A.①②
B.①③
C.①③④
D.①④⑤
(10题)
(11题)
(12题)
11、直角、如图放置,其中,且.若,,.则的长为(
)
A.
B.
C.
D.
12、如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
13、如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4.5cm2
C.5cm2
D.6cm2
14、程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
其中所有正确结论的序号是(
)
A.②③
B.③④
C.②③④
D.①②③④
二、填空题
15、如图,,,只添加一个条件使,你添加的条件是_________.
(15题)
(16题)
16、要测量河两岸相对的两点A,B间的距离(AB垂直于河岸BF),先在BF上取两点C,D,使CD=CB,再作出BF的垂线DE,且使A,C,E三点在同一条直线上,如图,可以得△EDC≌△ABC,所以ED=AB.因此测得ED的长就是AB的长.判定△EDC≌△ABC的理由是____________.
17、如图,在△ABC中,AB=AC,BE、CF是中线,则由______可得△AFC≌△AEB.
(17题)
(18题)
(19题)
(20题)
18、尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP.
由作法得△OCP≌△ODP的根据是_________.
19、如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
20、如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是__________
21、如图,在Rt△ABC中,∠ABC=90°,BC=5,BD⊥AC于点D,点E在边AB上,且BE=BC,过点E作EF⊥AB交BD延长线于点F,若EF=12,则AE=_____.
(21题)
(22题)
(23题)
(24题)
22、如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
23、已知中,,,点为的中点,点、分别为边、上的动点,且,连接,下列说法正确的是______.(写出所有正确结论的序号)
①;②;③;④
24、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E、作QF⊥l于F,当点P运动
秒时,以P、E、C为顶点的三角形和以Q、F、C为顶点的三角形全等.
三、解答题
25、如图,已知,,,,
试猜想与的位置关系并说明理由.
26、如图,已知在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4,求证:∠5=∠6.
27、如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC,
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
28、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,
求证:CB=CD.
29、已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
30、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE为多少?说明理由;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?
请直接写出你的结论,不需证明.
第一章
阶段培优练习题(练习范围1.3--SAS、ASA、AAS、SSS)
2021-2022学年苏科版八年级数学上册
一、选择题
1、根据下列已知条件,能画出唯一的△ABC的是(
)
A.,,
B.,,
C.,
D.,,
【答案】B
【解析】A、不符合三角形三边之间的关系,不能作出三角形,错误;
B、符合全等三角形判定中的SSS,正确;
C、只有两个条件,不足以构成三角形,错误;
D、三个角不能画出唯一的三角形,错误,
故选B.
2、如图,点A,E,B,F在一条直线上,在△ABC和△FED中,AC=FD,BC=DE,要利用“SSS”来判定△ABC≌△FED时,下面4个条件中:①AE=FB;②AB=FE;③AE=BE;④BF=BE;可利用的是(
)
A.①或②
B.②或③
C.③或①
D.①或④
【答案】A
【解析】
试题解析:由题意可得,要用SSS进行△ABC和△FED全等的判定,需要AB=FE,
若添加①AE=FB,则可得AE+BE=FB+BE,即AB=FE,故①可以;
若添加AB=FE,则可直接证明两三角形的全等,故②可以,
若添加AE=BE,或BF=BE,均不能得出AB=FE,不可以利用SSS进行全等的证明,故③④不可以.
故选A.
3、如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF,不能添加的一组条件是(
)
A.∠B=∠E,BC=EF
B.∠A=∠D,BC=EF
C.∠A=∠D,∠B=∠E
D.BC=EF,AC=DF
【答案】B
【分析】根据全等三角形的判定定理对选项逐一进行判断即可.
【详解】添加∠B=∠E,BC=EF可用SAS判定两个三角形全等,故A选项不符合题意,
添加∠A=∠D,BC=EF是SSA,不能判定两个三角形全等,故B选项符合题意,
添加∠A=∠D,∠B=∠E可用ASA判定两个三角形全等,故C选项不符合题意,
添加BC=EF,AC=DF可用SSS判定两个三角形全等,故D选项不符合题意.
故选B.
4、如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是
A.∠A=∠C
B.AD=CB
C.BE=DF
D.AD∥BC
【答案】B
【解析】
试题分析:∵AE=CF,∴AE+EF=CF+EF.∴AF=CE.
A.∵在△ADF和△CBE中,,∴△ADF≌△CBE(ASA),正确,故本选项错误.
B.根据AD=CB,AF=CE,∠AFD=∠CEB不能推出△ADF≌△CBE,错误,故本选项正确.
C.∵在△ADF和△CBE中,,∴△ADF≌△CBE(SAS),正确,故本选项错误.
D.∵AD∥BC,∴∠A=∠C.由A选项可知,△ADF≌△CBE(ASA),正确,故本选项错误.
故选B.
5、如图,AE=AF,AB=AC,EC与BF交于点O,∠A=60°,∠B=25°,则∠EOB的度数为(
)
A.60°
B.70°
C.75°
D.85°
【答案】B
【解析】
试题解析:
故选B.
6、如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6
B.0.8
C.1
D.1.6
【分析】根据AAS证明△DBF与△ABC全等,利用全等三角形的性质解答即可.
【解析】∵DE⊥AC于E,∴∠FDB+∠C=90°,
∵∠ABC=90°,∴∠D+∠DFB=90°,∴∠C=∠BFD,
在△DBF与△ABC中,
∴△DBF≌△ABC(AAS),∴BF=BC,
∵DC=2.6,BF=1,
∴AF=AB﹣BF=BD﹣BF=DC﹣BF﹣BF=2.6﹣1﹣1=0.6,
故选:A.
7、如图,在△ABC中,∠A=50°,∠B=∠C,点D,E,F分别在边BC,CA,AB上,且满足BF=CD,BD=CE,∠BFD=30°,则∠FDE的度数为( )
A.75°
B.80°
C.65°
D.95°
【分析】由∠B=∠C,∠A=50°,利用三角形内角和为180°得∠B=65°,∠FDB=85°,再由BF=CD,BD=CE,利用SAS得到△BDF≌△CED,利用全等三角形对应角相等得到∠BFD=∠CDE,利用三角形内角和即可得证.
【解析】∵∠B=∠C,∠A=50°,∴∠B=∠C=×(180°﹣50°)=65°,
∵∠BFD=30°,∠BFD+∠B+∠FDB=180°,
∴∠FDB=85°
在△BDF和△CED中,
∴△BDF≌△CED(SAS),∴∠BFD=∠CDE=30°,
又∵∠FDE+∠FDB+∠CDE=180°,
∴∠FDE=180°﹣30°﹣85°=65°.
故选:C.
8、如图,已知△的六个元素,则下面甲、乙、丙三个三角形和△全等的图是(
)
A.甲和乙
B.乙和丙
C.只有乙
D.只有丙
【答案】B
【分析】根据全等三角形的判定方法进行逐个验证,做题时要找准对应边,对应角.
【详解】解:如图:
图甲不符合三角形全等的判定定理,即图甲和不全等;
在和中,?∴,
图乙符合定理,即图乙和全等;
在和中,∴,
图丙符合定理,即图丙和全等.
甲、乙、丙三个三角形中和全等的图形是:乙或丙.
故选:.
9、已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④∠BAE+∠DAC=180°.
其中结论正确的个数是(
)
A.1
B.2
C.3
D.4
【答案】D
【分析】①由AB=AC,AD=AE,利用等式的性质得到夹角相等,利用SAS得出△ABD≌△ACE,由全等三角形的对应边相等得到BD=CE;
②由△ABD≌△ACE得到一对角相等,再利用等腰直角三角形的性质及等量代换得到BD垂直于CE;
③由等腰直角三角形的性质得到∠ABD+∠DBC=45°,等量代换得到∠ACE+∠DBC=45°;
④由题意,∠BAE+∠DAC=360°-∠BAC-∠DAE=180°.
【详解】
解:①∵∠BAC=∠DAE=90°,
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD和△CAE中,,∴△BAD≌△CAE(SAS),∴BD=CE,本选项正确;
②∵△BAD≌△CAE,∴∠ABD=∠ACE,
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°,
∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°,则BD⊥CE,本选项正确;
③∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°,∴∠ABD+∠DBC=45°,
∵∠ABD=∠ACE,
∴∠ACE+∠DBC=45°,本选项正确;
④由题意,∠BAE+∠DAC=360°-∠BAC-∠DAE=360°-90°-90°=180°,本选项正确;
故选D.
10、如图,是的中线,,分别是和延长线上的点,且,连接,,下列说法:①和面积相等;
②;
③≌;④;⑤.其中正确的是(
)
A.①②
B.①③
C.①③④
D.①④⑤
【答案】C
【分析】根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE.
【详解】解:∵AD是△ABC的中线,∴BD=CD,∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,,∴△BDF≌△CDE(SAS),故③正确;
∴∠F=∠DEC,∴BF∥CE,故④正确;
∵△BDF≌△CDE,∴CE=BF,故⑤错误,
正确的结论为:①③④,
故选:C.
11、直角、如图放置,其中,且.若,,.则的长为(
)
A.
B.
C.
D.
【答案】C
【分析】先利用AAS证明,再根据全等三角形的性质进行线段和差计算即可.
【详解】解:,,,,,
在与中,;
,,
∵,,,,∴
故选C.
12、如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( )
A.1个
B.2个
C.3个
D.4个
【答案】B
【分析】将条件进行组合后,利用三角形全等的判定进行判断即可.
【详解】①②③为条件,根据SAS,可判定;可得结论④;
①②④为条件,根据SSS,可判定;可得结论③;
①③④为条件,SSA不能证明,
②③④为条件,SSA不能证明,
最多可以构成正确结论2个,故选B.
13、如图,△ABC的面积为9cm2,BP平分∠ABC,AP⊥BP于P,连接PC,则△PBC的面积为( )
A.3cm2
B.4.5cm2
C.5cm2
D.6cm2
【答案】B
【分析】根据已知条件证得△ABP≌△EBP,根据全等三角形的性质得到AP=PE,得出S△ABP=S△EBP,S△ACP=S△ECP,推出S△PBC=S△ABC,代入求出即可.
【详解】解:延长AP交BC于E,
∵BP平分∠ABC,∴∠ABP=∠EBP,
∵AP⊥BP,∴∠APB=∠EPB=90°,
在△ABP和△EBP中,,∴△ABP≌△EBP(ASA),
∴AP=PE,∴S△ABP=S△EBP,S△ACP=S△ECP,
∴S△PBC=S△ABC=×9cm2=4.5cm2,
故选:B.
14、程老师制作了如图1所示的学具,用来探究“边边角条件是否可确定三角形的形状”问题,操作学具时,点Q在轨道槽AM上运动,点P既能在以A为圆心、以8为半径的半圆轨道槽上运动,也能在轨道槽QN上运动,图2是操作学具时,所对应某个位置的图形的示意图.
有以下结论:①当∠PAQ=30°,PQ=6时,可得到形状唯一确定的△PAQ
②当∠PAQ=30°,PQ=9时,可得到形状唯一确定的△PAQ
③当∠PAQ=90°,PQ=10时,可得到形状唯一确定的△PAQ
④当∠PAQ=150°,PQ=12时,可得到形状唯一确定的△PAQ
其中所有正确结论的序号是(
)
A.②③
B.③④
C.②③④
D.①②③④
【答案】C
【分析】分别在以上四种情况下以P为圆心,PQ的长度为半径画弧,观察弧与直线AM的交点即为Q点,作出后可得答案.
【详解】如下图,当∠PAQ=30°,PQ=6时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现两个位置的Q都符合题意,所以不唯一,所以①错误.
如下图,当∠PAQ=30°,PQ=9时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现左边位置的Q不符合题意,所以唯一,所以②正确.
如下图,当∠PAQ=90°,PQ=10时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现两个位置的Q都符合题意,但是此时两个三角形全等,所以形状相同,所以唯一,所以③正确.
如下图,当∠PAQ=150°,PQ=12时,以P为圆心,PQ的长度为半径画弧,弧与直线AM有两个交点,作出,发现左边位置的Q不符合题意,所以唯一,所以④正确.
综上:②③④正确.
故选C.
二、填空题
15、如图,,,只添加一个条件使,你添加的条件是_________.
【答案】∠C=∠D或∠B=∠E或AB=AE
【分析】由已知∠1=∠2可得∠BAC=∠EAD,又有AC=AD,还缺少边或角对应相等的条件,结合判定方法及图形进行选择即可.可根据判定定理ASA、SAS尝试添加条件.
【详解】(1)添加∠C=∠D.
∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,∴∠CAB=∠DAE,
在△ABC与△AED中,,∴△ABC≌△AED(ASA);
(2)添加∠B=∠E.
∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,
∴∠CAB=∠DAE,
在△ABC与△AED中,,∴△ABC≌△AED(AAS);
(3)添加AB=AE,
∵∠1=∠2,∴∠1+∠BAD=∠2+∠BAD,∴∠CAB=∠DAE,
在△ABC与△AED中,,∴△ABC≌△AED(SAS),
故答案为:∠C=∠D或∠B=∠E或AB=AE.
16、要测量河两岸相对的两点A,B间的距离(AB垂直于河岸BF),先在BF上取两点C,D,使CD=CB,再作出BF的垂线DE,且使A,C,E三点在同一条直线上,如图,可以得△EDC≌△ABC,所以ED=AB.因此测得ED的长就是AB的长.判定△EDC≌△ABC的理由是____________.
【答案】ASA
【分析】由已知可以得到∠ABC=∠BDE=90°,又CD=BC,∠ACB=∠DCE,由此根据角边角即可判定△EDC≌△ABC.
【详解】∵BF⊥AB,DE⊥BD,∴∠ABC=∠BDE
又∵CD=BC,∠ACB=∠DCE,∴△EDC≌△ABC(ASA)
故答案为ASA
17、如图,在△ABC中,AB=AC,BE、CF是中线,则由______可得△AFC≌△AEB.
【答案】:SAS.
【解析】
【分析】由AB=AC,BE、CF是中线可知AE=AF,由∠A是公共角,AB=AC即可根据SAS证明△AFC≌△AEB.
【详解】∵BE、CF是中线,∴AF=AB,AE=AC,
∵AB=AC∴AE=AF,
∵AE=AF,∠A=∠A,AB=AC,∴△AFC≌△AEB(SAS).
故答案为SAS
18、尺规作图作∠AOB的平分线方法如下:以O为圆心,任意长为半径画弧交OA,OB于C,D,再分别以点C,D为圆心,以大于长为半径画弧,两弧交于点P,作射线OP.
由作法得△OCP≌△ODP的根据是_________.
【答案】SSS
【解析】
解:∵以O为圆心,任意长为半径画弧交OA,OB于C,D,即OC=OD.以点C,D为圆心,以大于CD长为半径画弧,两弧交于点P,即CP=DP.在△OCP和△ODP中,∵OC=OD,OP=OP,CP=DP,∴△OCP≌△ODP(SSS).故答案为SSS.
19、如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3= .
【分析】求出∠BAD=∠EAC,证△BAD≌△CAE,推出∠2=∠ABD=30°,根据三角形的外角性质求出即可.
【解析】∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠1=∠EAC,
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴∠2=∠ABD=30°,
∵∠1=25°,∴∠3=∠1+∠ABD=25°+30°=55°,
故答案为:55°.
20、如图所示,AD是△ABC中BC边上的中线,若AB=2,AC=6,则AD的取值范围是__________
【答案】2<AD<4
【分析】此题要倍长中线,再连接,构造全等三角形.根据三角形的三边关系:任意两边之和大于第三边,任意两边之差小于第三边.即可求解.
【详解】
解:延长AD到E,使AD=DE,连接BE,
∵AD是△ABC的中线,∴BD=CD,
在△ADC与△EDB中,∴△ADC≌△EDB(SAS),∴EB=AC,
根据三角形的三边关系定理:6-2<AE<6+2,
∴2<AD<4,
故AD的取值范围为2<AD<4.
21、如图,在Rt△ABC中,∠ABC=90°,BC=5,BD⊥AC于点D,点E在边AB上,且BE=BC,过点E作EF⊥AB交BD延长线于点F,若EF=12,则AE=_____.
【答案】7
【分析】由题意知:BD⊥AC,EF⊥AB,∠ADB=∠FEB=90°,∠A=∠F,△ABC≌△FEB(AAS),
AB=EF=12,AE=7.
【详解】解:∵BD⊥AC,EF⊥AB,∴∠ADB=∠FEB=90°,
∴∠A+∠ABD=∠F+∠FBE=90°,∴∠A=∠F,
在△ABC和△FEB中,
,∴△ABC≌△FEB(AAS),
∴AB=EF=12,
∵BE=BC=5,∴AE=AB﹣BE=7.
故填:7.
22、如图,在△ABE和△ACF中,EB交AC于点M,交FC于点D,AB交FC于点N,∠E=∠F=90°,∠B=∠C,AE=AF.下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中,正确的是_________.(填序号)
【答案】①②③
【分析】∠E=∠F=90°,∠B=∠C,AE=AF可得△ABE≌△ACF,三角形全等的性质BE=CF;∠BAE=∠CAF可得①∠1=∠2;由ASA可得△ACN≌△ABM.④CD=DN不成立.
【详解】解:∵∠E=∠F=90°,∠B=∠C,AE=AF,∴△ABE≌△ACF,
∴BE=CF,
∠BAE=∠CAF
∠BAE-∠BAC=∠CAF-∠BAC,
∴∠1=∠2
△ABE≌△ACF,
∴∠B=∠C,AB=AC
又∠BAC=∠CAB,
△ACN≌△ABM.
④CD=DN不能证明成立,3个结论对.
故答案是:①②③
23、已知中,,,点为的中点,点、分别为边、上的动点,且,连接,下列说法正确的是______.(写出所有正确结论的序号)
①;②;③;④
【答案】①②④
【分析】
根据补角的性质计算可得①;连接D,证明,根据三角形全等的性质判断可得后面的结果;
【详解】,
,
,
;故①正确;
连接AD,
∵,,∴,
又∵点为的中点,
∴,,,即,
又∵,∴,
又∵,∴,
在△BED和△AFD中,,∴,∴ED=FD;故②正确;
∵,∴,
则,故④正确;
当点E移动到点A时,此时点F与点C重合,很明显此时EF=AC,FC=0,即;故③错误;
故答案为①②④.
24、如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A→C→B路径向终点运动,终点为B点;点Q从B点出发沿B→C→A路径向终点运动,终点为A点.点P和Q分别以每秒1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E、作QF⊥l于F,当点P运动
秒时,以P、E、C为顶点的三角形和以Q、F、C为顶点的三角形全等.
【解题思路】根据题意分为五种情况,根据全等三角形的性质得出CP=CQ,代入得出关于t的方程,解方程即可.
【解答过程】解:分为五种情况:
①如图1,P在AC上,Q在BC上,则PC=6﹣t,QC=8﹣3t,
∵PE⊥l,QF⊥l,∴∠PEC=∠QFC=90°,
∵∠ACB=90°,∴∠EPC+∠PCE=90°,∠PCE+∠QCF=90°,∴∠EPC=∠QCF,
∵△PCE≌△CQF,∴PC=CQ,即6﹣t=8﹣3t,t=1;
②如图2,P在BC上,Q在AC上,则PC=t﹣6,QC=3t﹣8,
∵由①知:PC=CQ,∴t﹣6=3t﹣8,t=1;t﹣6<0,即此种情况不符合题意;
③当P、Q都在AC上时,如图3,CP=6﹣t=3t﹣8,t=;
④当Q到A点停止,P在BC上时,AC=PC,t﹣6=6时,解得t=12.
⑤P和Q都在BC上的情况不存在,因为P的速度是每秒1cm,Q的速度是每秒3cm;
答:点P运动1或或12秒时,以P、E、C为顶点的三角形上以O、F、C为顶点的三角形全等.
故答案为:1或或12.
三、解答题
25、如图,已知,,,,
试猜想与的位置关系并说明理由.
【答案】.理由见解析
【解析】
试题分析:根据SSS证明△ABD≌△ACE,从而得∠BAD=∠CAE,再由∠CAD是公共角,从而可得∠DAE=∠BAC=90°,从而得到AD⊥AE.
试题解析:∵AB⊥AC,∴∠BAC=90°,
在△ABD和△ACE中,∴△ABD≌△ACE(SSS),∴∠BAD=∠CAE,
∴∠BAD-∠CAD=∠CAE-∠CAD,
即∠DAE=∠BAC=90°,
∴AD⊥AE.
26、如图,已知在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4,求证:∠5=∠6.
【答案】证明见解析
【分析】因为∠1=∠2,∠3=∠4,AC=CA,根据ASA易证△ADC≌△ABC,所以有DC=BC,又因为∠3=∠4,EC=CE,则可根据SAS判定△CED≌△CEB,故∠5=∠6.
【详解】
证明:∵,∴△ADC≌△ABC(ASA).∴DC=BC.
又∵,∴△CED≌△CEB(SAS).∴∠5=∠6.
27、如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC,
(1)试说明:∠A=∠C;
(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?
【答案】(1)见解析;(2)构造全等三角形.
【分析】(1)根据题意,没有证明两三角形全等的条件,所以要作条辅助线,连接OE;然后就可以利用SSS全等判定定理证明两三角形全等,继而∠A=∠C,本题即可证明;
(2)说明OE的意义即可.
【详解】(1)如图,连接OE.
在△EAO和△ECO中,,所以△EAO≌△ECO(SSS).
所以∠A=∠C(全等三角形的对应角相等).
(2)
在(1)的解答过程中,需要作辅助线,它的意图是构造全等三角形.
28、如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,
求证:CB=CD.
【分析】连接AC,先利用SSS证明△ACE≌△ACF,可得∠EAC=∠FAC,再利用AAS证明△ACB≌△ACD即可得结论.
【解答】证明:如图,连接AC,
在△ACE和△ACF中,
∴△ACE≌△ACF(SSS),∴∠EAC=∠FAC,
在△ACB和△ACD中,
∴△ACB≌△ACD(AAS),∴CB=CD.
29、已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.
(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;
(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.
【答案】(1)见解析
(2)见解析
(3)BD=DE-CE
【解析】此题考查了全等三角形的判定与性质,以及等腰直角三角形的性质,利用了转化及等量代换的思想,熟练掌握全等三角形的判定与性质是解本题的关键.
(1)由BD垂直于AE,得到三角形ABD为直角三角形,利用直角三角形两锐角互余得到一对角互余,再由∠BAC=90°,得到一对角互余,利用同角的余角相等得到一对角相等,再由一对直角相等,AB=AC,利用AAS可得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=AD+DE,等量代换即可得证;
(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系为BD=DE-CE,理由为:同(1)得出三角形ABD与三角形ACE全等,由全等三角形的对应边相等得到AD=CE,BD=AE,由AE=DE-AD等量代换即可得证;
(3)由(1)(2)总结得到当D、E位于直线BC异侧时,BD=DE+CE;当D、E位于直线BC同侧时,BD=DE-CE.
解:(1)证明:∵BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°,∴∠ABD+∠BAD=90°,
∵∠BAC=90°,∴∠BAD+∠EAC=90°,∴∠ABD=∠EAC,
在△ABD和△CAE中∵
∴△ABD≌△CAE(AAS),∴AD=CE,BD=AE,
∵AE=AD+DE,∴BD=DE+CE;
(2)BD、DE、CE的关系为BD=DE-CE,理由为:
证明:在△ABD和△CAE中
△ABD≌△CAE(AAS),∴AD=CE,BD=AE,
∵AE=DE-AD,∴BD=DE-CE;
(3)当D、E位于直线BC异侧时,BD=DE+CE;
当D、E位于直线BC同侧时,BD=DE-CE.
30、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE为多少?说明理由;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?
请直接写出你的结论,不需证明.
【答案】(1)90°;(2)①α+β=180°,理由见详解;②点D在直线BC上移动,α+β=180°或α=β.
【分析】(1)由等腰直角三角形的性质可得∠ABC=∠ACB=45°,由“SAS”可证△BAD≌△CAE,可得∠ABC=∠ACE=45°,可求∠BCE的度数;
(2)①由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论;②分两种情况画出图形,由“SAS”可证△ABD≌△ACE得出∠ABD=∠ACE,再用三角形的内角和即可得出结论.
【详解】解:(1)∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,
∵∠DAE=∠BAC,∴∠BAD=∠CAE,且AB=AC,AD=AE,
∴△BAD≌△CAE(SAS)
∴∠ABC=∠ACE=45°,∴∠BCE=∠ACB+∠ACE=90°;
(2)①α+β=180°,
理由:∵∠BAC=∠DAE,∴∠BAC?∠DAC=∠DAE?∠DAC.即∠BAD=∠CAE.
在△ABD与△ACE中,,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.
∴∠B+∠ACB=∠ACE+∠ACB.
∵∠ACE+∠ACB=β,∴∠B+∠ACB=β,
∵α+∠B+∠ACB=180°,∴α+β=180°;
②如图1:当点D在射线BC上时,α+β=180°,
连接CE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,
在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,
在△ABC中,∠BAC+∠B+∠ACB=180°,
∴∠BAC+∠ACE+∠ACB=∠BAC+∠BCE=180°,
即:∠BCE+∠BAC=180°,∴α+β=180°,
如图2:当点D在射线BC的反向延长线上时,α=β.
连接BE,∵∠BAC=∠DAE,∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,
∴∠ABD=∠ACE=∠ACB+∠BCE,
∴∠ABD+∠ABC=∠ACE+∠ABC=∠ACB+∠BCE+∠ABC=180°,
∵∠BAC=180°?∠ABC?∠ACB,∴∠BAC=∠BCE.∴α=β;
综上所述:点D在直线BC上移动,α+β=180°或α=β.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
