2021-2022学年苏科版九年级数学上册2.1圆-2.4圆周角(2)培优训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册2.1圆-2.4圆周角(2)培优训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 11:34:35 | ||
图片预览


文档简介
2.1圆~2.4圆周角(2)
-2021-2022学年苏科版九年级数学上册
培优训练
一、选择题
1、若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P与⊙A的位置关系是( )
A.P在⊙A上
B.P在⊙A内
C.P在⊙A外
D.不确定
2、下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧.其中错误的结论有( )
A.1个
B.2个
C.3个
D.0个
3、P为⊙O内一点,,⊙O半径为5,则经过P点的最短弦长为(
)
A.5
B.6
C.8
D.10
4、如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( )
A.60°
B.70°
C.80°
D.90°
(4题)
(5题)
(6题)
(7题)
5、如图,在正方形网格中,一条圆弧经过,,三点,那么点在这条圆弧所在圆的(
).
A.内部
B.外部
C.圆上
D.不能确定
6、如图,A,B,C是半径为1的⊙O上的三个点,若AB=,∠CAB=30°,则∠ABC的度数为(
)
A.95°
B.100°
C.105°
D.110°
7、如图,四边形内接于,、为其两条对角线,,,,连接,则的大小为(
)
A.
B.
C.
D.
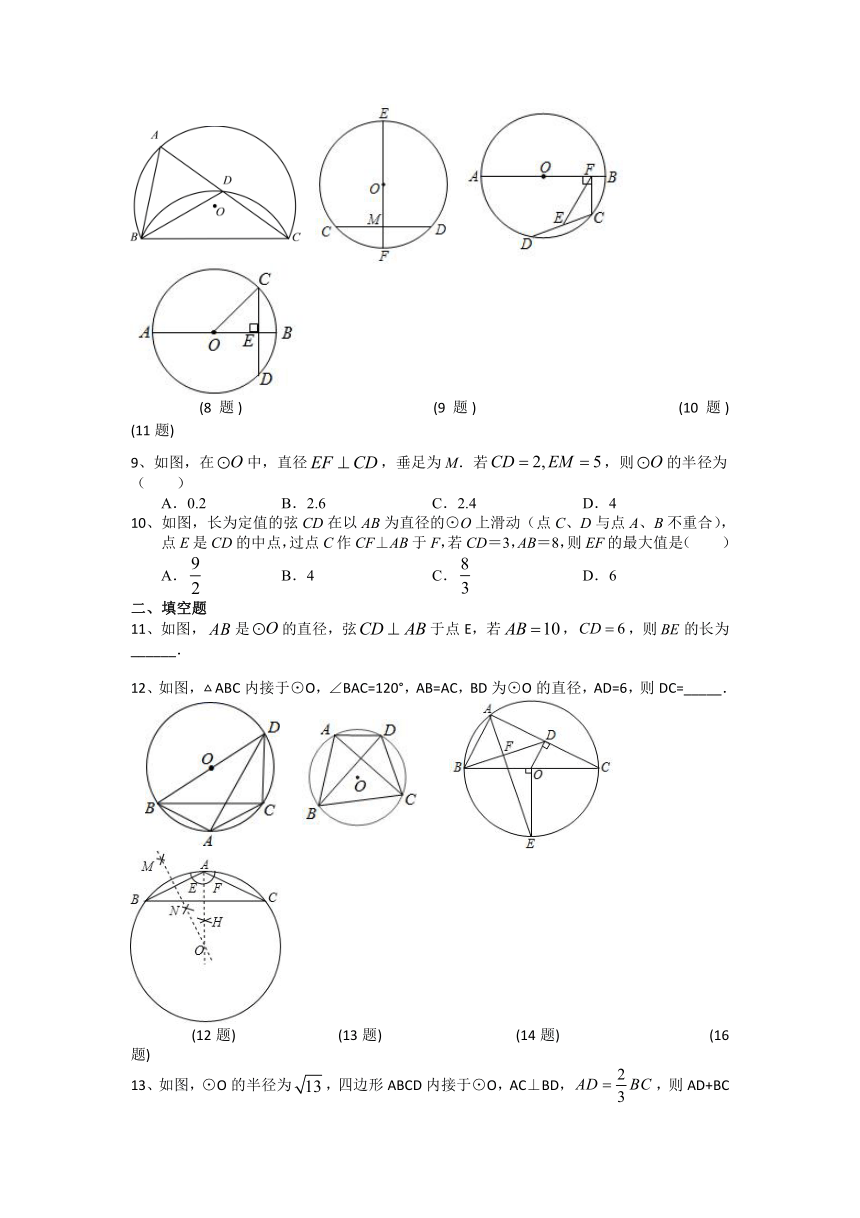
8、如图,△ABC内接于⊙O,将沿BC翻折,交AC于点D,连接BD,若∠BAC=66°,则∠ABD的度数是(
)
A.66
B.44
C.46
D.48
(8题)
(9题)
(10题)
(11题)
9、如图,在中,直径,垂足为M.若,则的半径为(
)
A.0.2
B.2.6
C.2.4
D.4
10、如图,长为定值的弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),点E是CD的中点,过点C作CF⊥AB于F,若CD=3,AB=8,则EF的最大值是( )
A.
B.4
C.
D.6
二、填空题
11、如图,是的直径,弦于点E,若,,则的长为______.
12、如图,ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC=_____.
(12题)
(13题)
(14题)
(16题)
13、如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,,则AD+BC的值为_____.
14、如图所示,已知内接于,是的直径,于点D,连接,半径,连接于点F,若,则______.
15、已知直线l:y=x?4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为______时,过P,A,B三点不能作出一个圆.
16、如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;③以点O为圆心,线段OA长为半径作圆.则⊙O的半径为______.
17、已知⊙O是△ABC的外接圆,⊙O的半径为2,AB=2,AC=2,则∠BAC= .
18、如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
(18题)
(19题)
(20题)
19、如图Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于
.
20、如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是AB的中点,点E是以点B为圆心,BD长为半径的圆上的一动点,连接AE,点F为AE的中点,则CF长度的最大值是
.
三、解答题
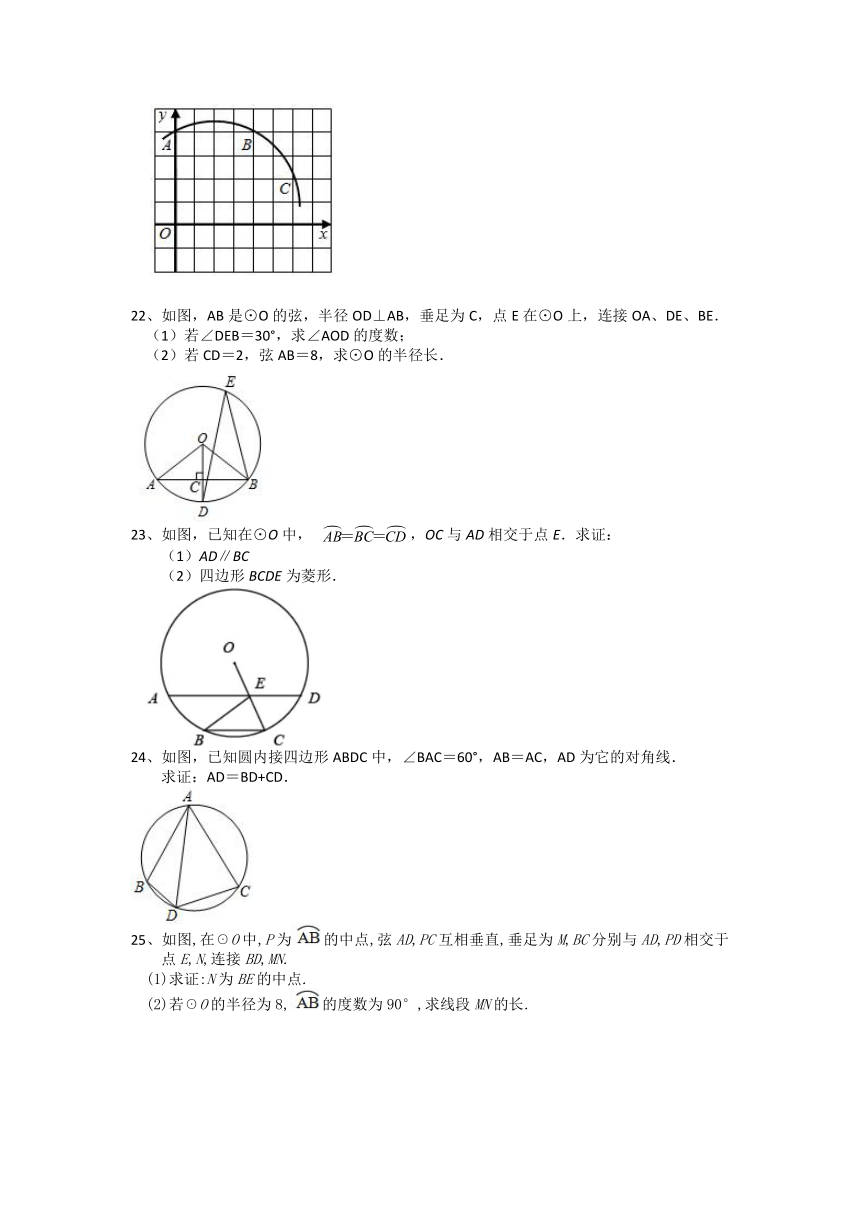
21、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
;
(2)这个圆的半径为
;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M
(填内、外、上).
22、如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.
(1)若∠DEB=30°,求∠AOD的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
23、如图,已知在⊙O中,
,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
24、如图,已知圆内接四边形ABDC中,∠BAC=60°,AB=AC,AD为它的对角线.
求证:AD=BD+CD.
25、如图,在☉O中,P为的中点,弦AD,PC互相垂直,垂足为M,BC分别与AD,PD相交于点E,N,连接BD,MN.
(1)求证:N为BE的中点.
(2)若☉O的半径为8,的度数为90°,求线段MN的长.
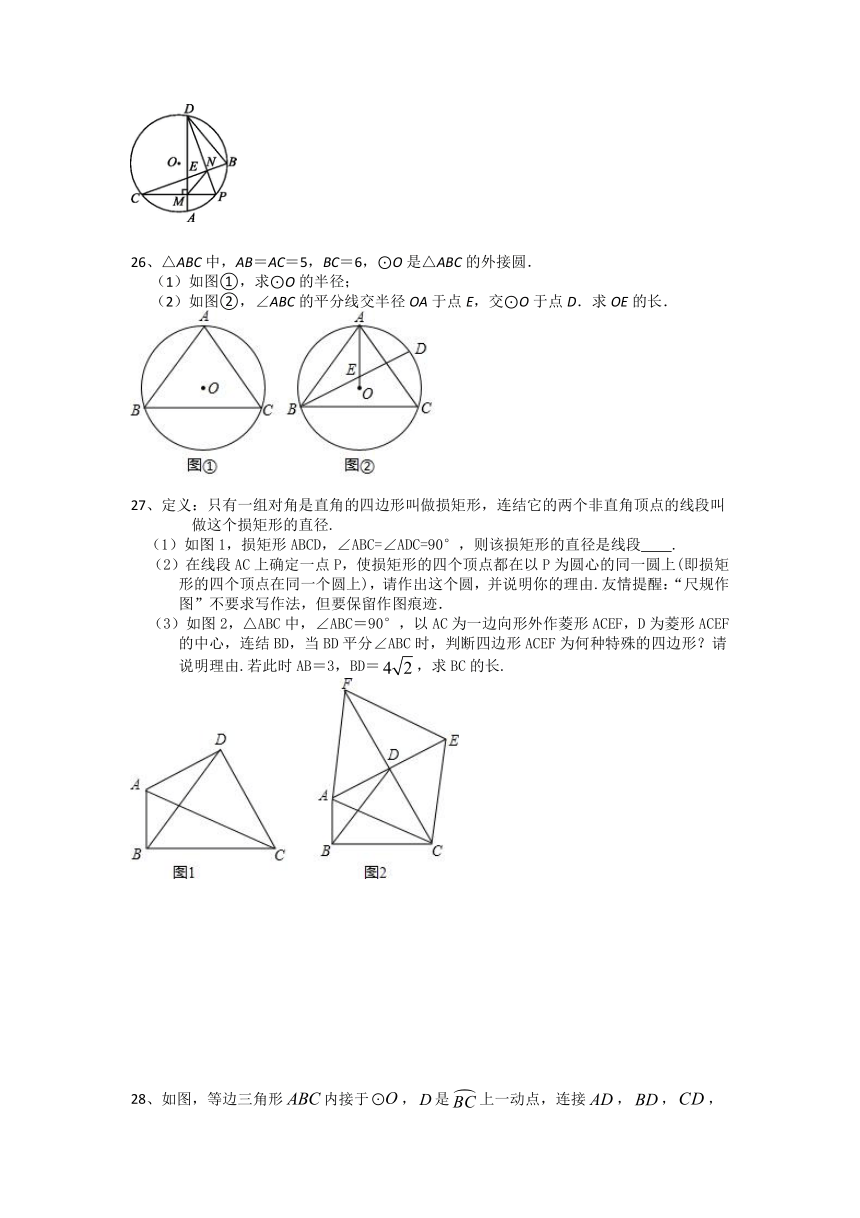
26、△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
27、定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段
.
(2)在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由.友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
(3)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.若此时AB=3,BD=,求BC的长.
28、如图,等边三角形内接于,是上一动点,连接,,,延长到点,使,连接.
(1)求证:是等边三角形;
(2)填空:①若,,则的长为____________;
②当的度数为_________时,四边形为菱形.
2.1圆~2.4圆周角(2)
-2021-2022学年苏科版九年级数学上册
培优训练(有答案)
一、选择题
1、若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P与⊙A的位置关系是( )
A.P在⊙A上
B.P在⊙A内
C.P在⊙A外
D.不确定
【点拨】首先根据两点的坐标求得两点之间的距离,然后利用两点之间的距离和圆A的半径求得点与圆的位置关系.
【解析】解:∵A的坐标为(3,4),点P的坐标是(5,8),∴AP==2,
∵⊙A的半径为5,
∴点P在⊙A的内部
故选:B.
2、下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧.其中错误的结论有( )
A.1个
B.2个
C.3个
D.0个
解:①任意三点确定一个圆;错误,应该是不在同一直线上的三点可以确定一个圆;
②相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中;
③平分弦的直径垂直于弦;并且平分弦所对的弧,错误,此弦不是直径;
故选:C.
3、P为⊙O内一点,,⊙O半径为5,则经过P点的最短弦长为(
)
A.5
B.6
C.8
D.10
【答案】C
【分析】根据勾股定理和垂径定理即可求得.
【详解】解:在过点P的所有⊙O的弦中,
如图,当弦与OP垂直时,弦最短,
此时,
得其半弦长为4,则弦长是8,
故选:C.
4、如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( )
A.60°
B.70°
C.80°
D.90°
解:∵点O为△ABC的外心,∠A=40°,
∴∠A=∠BOC,
∴∠BOC=2∠A=80°,
故选:C.
5、如图,在正方形网格中,一条圆弧经过,,三点,那么点在这条圆弧所在圆的(
).
A.内部
B.外部
C.圆上
D.不能确定
【分析】根据弦的中垂线的交点是弧所在圆的圆心,先确定圆心的位置,再求出半径,最后根据点和圆心的距离,判断点和圆的位置关系.
【详解】
如图,根据弦的中垂线的交点是弧所在圆的圆心,确定圆心为O,
∵
,∴点M在圆上,
故选C.
6、如图,A,B,C是半径为1的⊙O上的三个点,若AB=,∠CAB=30°,则∠ABC的度数为(
)
A.95°
B.100°
C.105°
D.110°
【答案】C
【解析】解:如图,连接OB,OC,
∵OA=OB=1,AB=,∴OA2+OB2=AB2,∴∠AOB=90°,
又∵OA=OB,∴∠ABO=∠BAO=45°,
∵∠CAB=30°,∴∠COB=2∠CAB=60°,
又∵OC=OB,∴∠OBC=∠OCB=60°,
∴∠ABC=∠ABO+∠OBC=105°,故选:C.
7、如图,四边形内接于,、为其两条对角线,,,,连接,则的大小为(
)
A.
B.
C.
D.
【答案】A
【解析】∵,,∴,,
∴.
∵,∴,∴.
∴,
∴.
∵,∴.
故选A.
8、如图,△ABC内接于⊙O,将沿BC翻折,交AC于点D,连接BD,若∠BAC=66°,则∠ABD的度数是(
)
A.66
B.44
C.46
D.48
【答案】D
【分析】根据折叠的性质和圆内接四边形的性质得到∠A+∠BDC=180°,求得∠BDC的度数,再根据三角形的外角性质即可求得结果.
【解析】解:如图,补全翻折前的图形,点与点关于BC对称,∴,
∵四边形内接于⊙O,∴,∴,
∵,∴,
∵,∴,
故选:D.
9、如图,在中,直径,垂足为M.若,则的半径为(
)
A.0.2
B.2.6
C.2.4
D.4
【答案】B
【分析】连接OC,设⊙O的半径为R,则OC=R,OM=5-R,根据垂径定理求出CM,根据勾股定理得出方程,求出即可.
【详解】解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,
∵直径EF⊥CD,垂足为M,CD=2,∴CM=DM=1,
在Rt△OMC中,由勾股定理得:OC2=OM2+CM2,
R2=(5-R)2+1?,解得R=2.6.
故选:B.
10、如图,长为定值的弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),点E是CD的中点,过点C作CF⊥AB于F,若CD=3,AB=8,则EF的最大值是( )
A.
B.4
C.
D.6
【答案】B
【分析】如图,延长CF交⊙O于T,连接DT.利用三角形的中位线定理证明EF=DT,当DT是直径时,EF的值最大.
【详解】解:如图,延长CF交⊙O于T,连接DT.
∵AB是直径,AB⊥CT,∴CF=FT,
∵点E是CD中点,∴EF=DT,
∴当DT是直径时,EF的值最大,最大值=×8=4,
故选:B.
二、填空题
11、如图,是的直径,弦于点E,若,,则的长为______.
【答案】1
【解析】解:∵是的直径,,∴,
∵,,∴,
∴,∴,
故答案为1.
12、如图,ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC=_____.
【答案】
【解析】∵BD为⊙O的直径,∴∠BAD=∠BCD=90°.
∵∠BAC=120°,∴∠CAD=120°﹣90°=30°.∴∠CBD=∠CAD=30°.
又∵∠BAC=120°,∴∠BDC=180°﹣∠BAC=180°﹣120°=60°.
∵AB=AC,∴∠ADB=∠ADC.∴∠ADB=∠BDC=×60°=30°.
∵AD=6,∴在Rt△ABD中,.
在Rt△BCD中,.
13、如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,,则AD+BC的值为_____.
【答案】10
【解析】解:作直径BE,连接DE,EC.
∵BE是直径,∴∠BDE=∠BCE=90°,∴BD⊥DE,
∵AC⊥BD,∴DE∥AC,
∴∠CDE=∠ACD,∴=,∴AD=EC,
∵AD=BC,∴EC=BC,∴可以假设EC=2k,BC=3k,
∵BC2+EC2=BE2,∴(3k)2+(2k)2=()2,
∴k=2或﹣2(舍弃),
∴BC=6,EC=4,∴AD=EC=4,
∴AD+BC=10,故答案为10.
14、如图所示,已知内接于,是的直径,于点D,连接,半径,连接于点F,若,则______.
【答案】
【解析】解:是的直径,,
,,,
,
,,,
,,
设,则,
,,,解得..
,,,
,,
故答案为:.
15、已知直线l:y=x?4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为______时,过P,A,B三点不能作出一个圆.
【解析】设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,解得,∴y=?x+2.
解方程组,得,
∴当P的坐标为(3,?1)时,过P,A,B三点不能作出一个圆.故答案为(3,?1).
16、如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;③以点O为圆心,线段OA长为半径作圆.则⊙O的半径为______.
【答案】5
【分析】如图,设交于.解直角三角形求出,再在中,利用勾股定理构建方程即可解决问题.
【详解】解:如图,设交于.半径为,
,平分,,,
,
在中,则有,
解得,
故答案为:5.
17、已知⊙O是△ABC的外接圆,⊙O的半径为2,AB=2,AC=2,则∠BAC= .
【分析】当AB和AC在OA的两旁,连接OA、OB、OC,如图,先证明△OAB为等边三角形得到∠BAO=60°,再利用勾股定理的逆定理证明△OAC为等腰直角三角形,则∠OAC=45°,则∠BAC=∠BAO+∠OAC=105°;当AB和AC在OA的同旁,如图,AB′=2,同理可得∠B′AC=∠B′AO﹣∠OAC=15°.
【解析】当AB和AC在OA的两旁,连接OA、OB、OC,如图,
∵AB=OB=OA=2,∴△OAB为等边三角形,∴∠BAO=60°,
∵OA=2,OC=2,AC=2,
∴OA2+OC2=AC2,∴△OAC为等腰直角三角形,∴∠OAC=45°,
∴∠BAC=∠BAO+∠OAC=60°+45°=105°;
当AB和AC在OA的同旁时,如图,AB′=2,
同理可得∠B′AC=∠B′AO﹣∠OAC=60°﹣45°=15°;
综上所述,∠BAC的度数为15°或105°.
故答案为15°或105°.
18、如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
解:连接CD,
∵AB=BC,∠BAC=30°,∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,∴∠D=180°﹣∠B=60°,
∵AD是直径,∴∠ACD=90°,
∵∠CAD=30°,AD=8,∴CD=AD=4,∴AC==4,
故答案为:4.
19、如图Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于
.
解:当点C关于直线BD的对称点落在⊙O上时,
则==45,
,
故答案为:2.
20、如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是AB的中点,点E是以点B为圆心,BD长为半径的圆上的一动点,连接AE,点F为AE的中点,则CF长度的最大值是
.
解:如图,延长AC到T,使得CT=AC,连接BT,TE,BE.
∵AC=CT,BC⊥AT,∴BA=BT,
∵∠ACB=90°,∠ABC=30°,BC=3,
∴∠BAT=60°,AC=BC?tan30°=3,
∴AB=2AC=6,∴△ABT是等边三角形,∴BT=AB=6,
∵AD=BD=BE,∴BE=3,
∵ET≤BT+BE,∴ET≤9,∴ET的最大值为9,
∵AC=CT,AF=FE,∴CF=ET,∴CF的最大值为.
故答案为:.
三、解答题
21、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
;
(2)这个圆的半径为
;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M
(填内、外、上).
【分析】(1),利用网格特点,作AB和BC的垂直平分线,它们的交点为M点,从而得到点M的坐标;
(2)利用两点间的距离公式计算出MA即可;
(3)先计算出DM,然后根据点与圆的位置关系的判定方法判断点D与⊙M的位置关系.
【解析】(1)如图,圆心M的坐标为(2,0);
(2)∵A(0,4),M(2,0),
即⊙M的半径为2;
(3)∵D(5,﹣2),M(2,0),
∵2,
∴点D在⊙M内.
故答案为(2,0);2;内.
22、如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.
(1)若∠DEB=30°,求∠AOD的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
【答案】(1)60°;(2)5.
【解析】解:(1)∵∠BOD=2∠DEB,∠DEB=30°,∴∠BOD=60°,
∵OD⊥AB,∴=,∴∠AOD=∠BOD=60°;
(2)设⊙O的半径为r,则OC=r?2,
∵OD⊥AB,∴AC=BC=AB=×8=4,
在Rt△OAC中,由勾股定理得:(r?2)2+42=r2,
解得:r=5,即⊙O的半径长为5.
23、如图,已知在⊙O中,
,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
【答案】(1)见解析;(2)见解析
【解析】解:(1)连接BD,
∵,∴∠ADB=∠CBD,∴AD∥BC;
(2)连接CD,
∵AD∥BC,∴∠EDF=∠CBF,
∵,∴BC=CD,∴BF=DF,又∠DFE=∠BFC,
∴△DEF≌△BCF(ASA),∴DE=BC,
∴四边形BCDE是平行四边形,又BC=CD,
∴四边形BCDE是菱形.
24、如图,已知圆内接四边形ABDC中,∠BAC=60°,AB=AC,AD为它的对角线.
求证:AD=BD+CD.
【答案】见解析.
【解析】解:连接BC,
∠BAC=60°,AB=AC,
△ABC为等边三角形,
∠ABC=∠ACB=60°,
∠ADC=∠ABC
∠ADB=∠ACB
在AD上取点E、F,使DE=DB、DF=DC,连接BE、CF,
∴△BDE、△CDF为等边三角形,
∴∠DEB=∠DFC=60°,
∴∠AEB=∠CFA=120°,
又∠FAC+∠FCA=∠DFC=60°、∠FAC+∠EAB=∠BAC=60°,∴∠EAB=∠FCA,
在△ABE和△CAF中,∵
,∴△ABE≌△CAF(AAS),
∴AE=CF,
∴AD=DE+AE=BD+FC=BD+CD.
25、如图,在☉O中,P为的中点,弦AD,PC互相垂直,垂足为M,BC分别与AD,PD相交于点E,N,连接BD,MN.
(1)求证:N为BE的中点.
(2)若☉O的半径为8,的度数为90°,求线段MN的长.
解:(1)证明∵AD⊥PC,∴∠EMC=90°.
∵P为的中点,∴=,∴∠ADP=∠BCP.
∵∠CEM=∠DEN,∴∠DNE=∠EMC=90°=∠DNB.
∵=,∴∠BDP=∠ADP,
∴∠DEN=∠DBN,∴DE=DB,∴EN=BN,∴N为BE的中点.
(2)如图,连接OA,OB,AB,AC.
∵的度数为90°,∴∠AOB=90°.∵OA=OB=8,∴AB=8.
由(1)同理得AM=EM.∵EN=BN,∴MN是△AEB的中位线,
∴MN=AB=4.
26、△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
【分析】(1)过A点作AH⊥BC于H,如图①,利用等腰三角形的性质得BH=CH=3,根据垂径定理的推论可判断点O在AH上,则利用勾股定理可计算出AH=4,连接OB,设⊙O的半径为r,在Rt△OBH中利用勾股定理得到32+(4﹣r)2=r2,然后解方程即可;
(2)作EF⊥AB于F,如图,根据角平分线的性质得到EH=EF,利用面积法得到,所以EH=AH=,然后利用(1)得OH=,从而计算EH﹣OH得到OE的长.
【解析】(1)过A点作AH⊥BC于H,如图①,
∵AB=AC,∴BH=CH=BC=3,即AH垂直平分BC,∴点O在AH上,
在Rt△ABH中,AH==4,
连接OB,设⊙O的半径为r,则OB=r,OH=AH﹣OA=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,解得r=,即⊙O的半径为;
(2)作EF⊥AB于F,如图,
∵BD平分∠ABC,∴EH=EF,
27、定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段
.
(2)在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由.友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
(3)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.若此时AB=3,BD=,求BC的长.
【解析】(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;
(2)
作图如图;
∵点P为AC中点,∴PA=PC=AC.
∵∠ABC=∠ADC=90°,∴BP=DP=AC,∴PA=PB=PC=PD,
∴点A、B、C、D在以P为圆心,AC为半径的同一个圆上.
(3)∵菱形ACEF,∴∠ADC=90°,AE=2AD,FC=2CD,∴四边形ABCD为损矩形,
∴由(2)可知,点A、B、C、D在同一个圆上.
∵AM平分∠BAD,∴∠ABD=∠CBD=45°,∴AD=CD,∴四边形ACEF为正方形.
∵点BD平分∠ABC,BD=,∴点D到AB、BC的距离h为4,
∴=6.
,
,,
∵,∴+=6+2BC,
∴BC=5或BC=-3(舍去),
∴BC=5.
28、如图,等边三角形内接于,是上一动点,连接,,,延长到点,使,连接.
(1)求证:是等边三角形;
(2)填空:①若,,则的长为____________;
②当的度数为_________时,四边形为菱形.
【答案】(1)证明见解析;(2)①3;②30°.
【解析】(1)∵△ABC是等边三角形,∴AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,
∵∠CBD与∠CAD是所对的圆周角,∴∠CBD=∠CAD,
同理可得:∠ABC=∠ADC=60°,
∵∠ACE=∠CAD+∠ADC,∴∠ACE=∠ABC+∠CBD=∠ABD,
在△ABD和△ACE中,,
∴△ABD≌△ACE,∴AD=AE,∴△ADE是等边三角形.
(2)①∵BD=CE=1,DE=CD+CE,CD=2,∴DE=3,
∵△ADE是等边三角形,∴AD=DE=3.
故答案为:3
②如图,连接OB、OC,
∵∠BAC和∠BOC分别是所对的圆周角和圆心角,∴∠BOC=2∠BAC=120°,
∵OB=OC,∴∠OCB=30°,
∵四边形为菱形,∴∠BCD=∠OCB=30°,
∵∠BAD和∠BCD都是所对的圆周角,∴∠BAD=∠BCD=30°,
∴当的度数为30°时,四边形为菱形.
故答案为:30°
-2021-2022学年苏科版九年级数学上册
培优训练
一、选择题
1、若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P与⊙A的位置关系是( )
A.P在⊙A上
B.P在⊙A内
C.P在⊙A外
D.不确定
2、下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧.其中错误的结论有( )
A.1个
B.2个
C.3个
D.0个
3、P为⊙O内一点,,⊙O半径为5,则经过P点的最短弦长为(
)
A.5
B.6
C.8
D.10
4、如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( )
A.60°
B.70°
C.80°
D.90°
(4题)
(5题)
(6题)
(7题)
5、如图,在正方形网格中,一条圆弧经过,,三点,那么点在这条圆弧所在圆的(
).
A.内部
B.外部
C.圆上
D.不能确定
6、如图,A,B,C是半径为1的⊙O上的三个点,若AB=,∠CAB=30°,则∠ABC的度数为(
)
A.95°
B.100°
C.105°
D.110°
7、如图,四边形内接于,、为其两条对角线,,,,连接,则的大小为(
)
A.
B.
C.
D.
8、如图,△ABC内接于⊙O,将沿BC翻折,交AC于点D,连接BD,若∠BAC=66°,则∠ABD的度数是(
)
A.66
B.44
C.46
D.48
(8题)
(9题)
(10题)
(11题)
9、如图,在中,直径,垂足为M.若,则的半径为(
)
A.0.2
B.2.6
C.2.4
D.4
10、如图,长为定值的弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),点E是CD的中点,过点C作CF⊥AB于F,若CD=3,AB=8,则EF的最大值是( )
A.
B.4
C.
D.6
二、填空题
11、如图,是的直径,弦于点E,若,,则的长为______.
12、如图,ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC=_____.
(12题)
(13题)
(14题)
(16题)
13、如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,,则AD+BC的值为_____.
14、如图所示,已知内接于,是的直径,于点D,连接,半径,连接于点F,若,则______.
15、已知直线l:y=x?4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为______时,过P,A,B三点不能作出一个圆.
16、如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;③以点O为圆心,线段OA长为半径作圆.则⊙O的半径为______.
17、已知⊙O是△ABC的外接圆,⊙O的半径为2,AB=2,AC=2,则∠BAC= .
18、如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
(18题)
(19题)
(20题)
19、如图Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于
.
20、如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是AB的中点,点E是以点B为圆心,BD长为半径的圆上的一动点,连接AE,点F为AE的中点,则CF长度的最大值是
.
三、解答题
21、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
;
(2)这个圆的半径为
;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M
(填内、外、上).
22、如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.
(1)若∠DEB=30°,求∠AOD的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
23、如图,已知在⊙O中,
,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
24、如图,已知圆内接四边形ABDC中,∠BAC=60°,AB=AC,AD为它的对角线.
求证:AD=BD+CD.
25、如图,在☉O中,P为的中点,弦AD,PC互相垂直,垂足为M,BC分别与AD,PD相交于点E,N,连接BD,MN.
(1)求证:N为BE的中点.
(2)若☉O的半径为8,的度数为90°,求线段MN的长.
26、△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
27、定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段
.
(2)在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由.友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
(3)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.若此时AB=3,BD=,求BC的长.
28、如图,等边三角形内接于,是上一动点,连接,,,延长到点,使,连接.
(1)求证:是等边三角形;
(2)填空:①若,,则的长为____________;
②当的度数为_________时,四边形为菱形.
2.1圆~2.4圆周角(2)
-2021-2022学年苏科版九年级数学上册
培优训练(有答案)
一、选择题
1、若⊙A的半径为5,圆心A的坐标为(3,4),点P的坐标是(5,8),则点P与⊙A的位置关系是( )
A.P在⊙A上
B.P在⊙A内
C.P在⊙A外
D.不确定
【点拨】首先根据两点的坐标求得两点之间的距离,然后利用两点之间的距离和圆A的半径求得点与圆的位置关系.
【解析】解:∵A的坐标为(3,4),点P的坐标是(5,8),∴AP==2,
∵⊙A的半径为5,
∴点P在⊙A的内部
故选:B.
2、下列有关圆的一些结论:①任意三点确定一个圆;②相等的圆心角所对的弧相等;③平分弦的直径垂直于弦;并且平分弦所对的弧.其中错误的结论有( )
A.1个
B.2个
C.3个
D.0个
解:①任意三点确定一个圆;错误,应该是不在同一直线上的三点可以确定一个圆;
②相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中;
③平分弦的直径垂直于弦;并且平分弦所对的弧,错误,此弦不是直径;
故选:C.
3、P为⊙O内一点,,⊙O半径为5,则经过P点的最短弦长为(
)
A.5
B.6
C.8
D.10
【答案】C
【分析】根据勾股定理和垂径定理即可求得.
【详解】解:在过点P的所有⊙O的弦中,
如图,当弦与OP垂直时,弦最短,
此时,
得其半弦长为4,则弦长是8,
故选:C.
4、如图,已知点O是△ABC的外心,∠A=40°,连结BO,CO,则∠BOC的度数是( )
A.60°
B.70°
C.80°
D.90°
解:∵点O为△ABC的外心,∠A=40°,
∴∠A=∠BOC,
∴∠BOC=2∠A=80°,
故选:C.
5、如图,在正方形网格中,一条圆弧经过,,三点,那么点在这条圆弧所在圆的(
).
A.内部
B.外部
C.圆上
D.不能确定
【分析】根据弦的中垂线的交点是弧所在圆的圆心,先确定圆心的位置,再求出半径,最后根据点和圆心的距离,判断点和圆的位置关系.
【详解】
如图,根据弦的中垂线的交点是弧所在圆的圆心,确定圆心为O,
∵
,∴点M在圆上,
故选C.
6、如图,A,B,C是半径为1的⊙O上的三个点,若AB=,∠CAB=30°,则∠ABC的度数为(
)
A.95°
B.100°
C.105°
D.110°
【答案】C
【解析】解:如图,连接OB,OC,
∵OA=OB=1,AB=,∴OA2+OB2=AB2,∴∠AOB=90°,
又∵OA=OB,∴∠ABO=∠BAO=45°,
∵∠CAB=30°,∴∠COB=2∠CAB=60°,
又∵OC=OB,∴∠OBC=∠OCB=60°,
∴∠ABC=∠ABO+∠OBC=105°,故选:C.
7、如图,四边形内接于,、为其两条对角线,,,,连接,则的大小为(
)
A.
B.
C.
D.
【答案】A
【解析】∵,,∴,,
∴.
∵,∴,∴.
∴,
∴.
∵,∴.
故选A.
8、如图,△ABC内接于⊙O,将沿BC翻折,交AC于点D,连接BD,若∠BAC=66°,则∠ABD的度数是(
)
A.66
B.44
C.46
D.48
【答案】D
【分析】根据折叠的性质和圆内接四边形的性质得到∠A+∠BDC=180°,求得∠BDC的度数,再根据三角形的外角性质即可求得结果.
【解析】解:如图,补全翻折前的图形,点与点关于BC对称,∴,
∵四边形内接于⊙O,∴,∴,
∵,∴,
∵,∴,
故选:D.
9、如图,在中,直径,垂足为M.若,则的半径为(
)
A.0.2
B.2.6
C.2.4
D.4
【答案】B
【分析】连接OC,设⊙O的半径为R,则OC=R,OM=5-R,根据垂径定理求出CM,根据勾股定理得出方程,求出即可.
【详解】解:连接OC,设⊙O的半径为R,则OC=R,OM=5-R,
∵直径EF⊥CD,垂足为M,CD=2,∴CM=DM=1,
在Rt△OMC中,由勾股定理得:OC2=OM2+CM2,
R2=(5-R)2+1?,解得R=2.6.
故选:B.
10、如图,长为定值的弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),点E是CD的中点,过点C作CF⊥AB于F,若CD=3,AB=8,则EF的最大值是( )
A.
B.4
C.
D.6
【答案】B
【分析】如图,延长CF交⊙O于T,连接DT.利用三角形的中位线定理证明EF=DT,当DT是直径时,EF的值最大.
【详解】解:如图,延长CF交⊙O于T,连接DT.
∵AB是直径,AB⊥CT,∴CF=FT,
∵点E是CD中点,∴EF=DT,
∴当DT是直径时,EF的值最大,最大值=×8=4,
故选:B.
二、填空题
11、如图,是的直径,弦于点E,若,,则的长为______.
【答案】1
【解析】解:∵是的直径,,∴,
∵,,∴,
∴,∴,
故答案为1.
12、如图,ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC=_____.
【答案】
【解析】∵BD为⊙O的直径,∴∠BAD=∠BCD=90°.
∵∠BAC=120°,∴∠CAD=120°﹣90°=30°.∴∠CBD=∠CAD=30°.
又∵∠BAC=120°,∴∠BDC=180°﹣∠BAC=180°﹣120°=60°.
∵AB=AC,∴∠ADB=∠ADC.∴∠ADB=∠BDC=×60°=30°.
∵AD=6,∴在Rt△ABD中,.
在Rt△BCD中,.
13、如图,⊙O的半径为,四边形ABCD内接于⊙O,AC⊥BD,,则AD+BC的值为_____.
【答案】10
【解析】解:作直径BE,连接DE,EC.
∵BE是直径,∴∠BDE=∠BCE=90°,∴BD⊥DE,
∵AC⊥BD,∴DE∥AC,
∴∠CDE=∠ACD,∴=,∴AD=EC,
∵AD=BC,∴EC=BC,∴可以假设EC=2k,BC=3k,
∵BC2+EC2=BE2,∴(3k)2+(2k)2=()2,
∴k=2或﹣2(舍弃),
∴BC=6,EC=4,∴AD=EC=4,
∴AD+BC=10,故答案为10.
14、如图所示,已知内接于,是的直径,于点D,连接,半径,连接于点F,若,则______.
【答案】
【解析】解:是的直径,,
,,,
,
,,,
,,
设,则,
,,,解得..
,,,
,,
故答案为:.
15、已知直线l:y=x?4,点A(0,2),点B(2,0),设点P为直线l上一动点,当P的坐标为______时,过P,A,B三点不能作出一个圆.
【解析】设直线AB的解析式为y=kx+b,
∵A(0,2),点B(2,0),
∴,解得,∴y=?x+2.
解方程组,得,
∴当P的坐标为(3,?1)时,过P,A,B三点不能作出一个圆.故答案为(3,?1).
16、如图,在等腰△ABC中,AB=AC=2,BC=8,按下列步骤作图:①以点A为圆心,适当的长度为半径作弧,分别交AB,AC于点E,F,再分别以点E,F为圆心,大于EF的长为半径作弧相交于点H,作射线AH;②分别以点A,B为圆心,大于AB的长为半径作弧相交于点M,N,作直线MN,交射线AH于点O;③以点O为圆心,线段OA长为半径作圆.则⊙O的半径为______.
【答案】5
【分析】如图,设交于.解直角三角形求出,再在中,利用勾股定理构建方程即可解决问题.
【详解】解:如图,设交于.半径为,
,平分,,,
,
在中,则有,
解得,
故答案为:5.
17、已知⊙O是△ABC的外接圆,⊙O的半径为2,AB=2,AC=2,则∠BAC= .
【分析】当AB和AC在OA的两旁,连接OA、OB、OC,如图,先证明△OAB为等边三角形得到∠BAO=60°,再利用勾股定理的逆定理证明△OAC为等腰直角三角形,则∠OAC=45°,则∠BAC=∠BAO+∠OAC=105°;当AB和AC在OA的同旁,如图,AB′=2,同理可得∠B′AC=∠B′AO﹣∠OAC=15°.
【解析】当AB和AC在OA的两旁,连接OA、OB、OC,如图,
∵AB=OB=OA=2,∴△OAB为等边三角形,∴∠BAO=60°,
∵OA=2,OC=2,AC=2,
∴OA2+OC2=AC2,∴△OAC为等腰直角三角形,∴∠OAC=45°,
∴∠BAC=∠BAO+∠OAC=60°+45°=105°;
当AB和AC在OA的同旁时,如图,AB′=2,
同理可得∠B′AC=∠B′AO﹣∠OAC=60°﹣45°=15°;
综上所述,∠BAC的度数为15°或105°.
故答案为15°或105°.
18、如图,△ABC是⊙O的内接三角形,AB=BC,∠BAC=30°,AD是直径,AD=8,则AC的长为
解:连接CD,
∵AB=BC,∠BAC=30°,∴∠ACB=∠BAC=30°,
∴∠B=180°﹣30°﹣30°=120°,∴∠D=180°﹣∠B=60°,
∵AD是直径,∴∠ACD=90°,
∵∠CAD=30°,AD=8,∴CD=AD=4,∴AC==4,
故答案为:4.
19、如图Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于
.
解:当点C关于直线BD的对称点落在⊙O上时,
则==45,
,
故答案为:2.
20、如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3,点D是AB的中点,点E是以点B为圆心,BD长为半径的圆上的一动点,连接AE,点F为AE的中点,则CF长度的最大值是
.
解:如图,延长AC到T,使得CT=AC,连接BT,TE,BE.
∵AC=CT,BC⊥AT,∴BA=BT,
∵∠ACB=90°,∠ABC=30°,BC=3,
∴∠BAT=60°,AC=BC?tan30°=3,
∴AB=2AC=6,∴△ABT是等边三角形,∴BT=AB=6,
∵AD=BD=BE,∴BE=3,
∵ET≤BT+BE,∴ET≤9,∴ET的最大值为9,
∵AC=CT,AF=FE,∴CF=ET,∴CF的最大值为.
故答案为:.
三、解答题
21、如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
;
(2)这个圆的半径为
;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M
(填内、外、上).
【分析】(1),利用网格特点,作AB和BC的垂直平分线,它们的交点为M点,从而得到点M的坐标;
(2)利用两点间的距离公式计算出MA即可;
(3)先计算出DM,然后根据点与圆的位置关系的判定方法判断点D与⊙M的位置关系.
【解析】(1)如图,圆心M的坐标为(2,0);
(2)∵A(0,4),M(2,0),
即⊙M的半径为2;
(3)∵D(5,﹣2),M(2,0),
∵2,
∴点D在⊙M内.
故答案为(2,0);2;内.
22、如图,AB是⊙O的弦,半径OD⊥AB,垂足为C,点E在⊙O上,连接OA、DE、BE.
(1)若∠DEB=30°,求∠AOD的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
【答案】(1)60°;(2)5.
【解析】解:(1)∵∠BOD=2∠DEB,∠DEB=30°,∴∠BOD=60°,
∵OD⊥AB,∴=,∴∠AOD=∠BOD=60°;
(2)设⊙O的半径为r,则OC=r?2,
∵OD⊥AB,∴AC=BC=AB=×8=4,
在Rt△OAC中,由勾股定理得:(r?2)2+42=r2,
解得:r=5,即⊙O的半径长为5.
23、如图,已知在⊙O中,
,OC与AD相交于点E.求证:
(1)AD∥BC
(2)四边形BCDE为菱形.
【答案】(1)见解析;(2)见解析
【解析】解:(1)连接BD,
∵,∴∠ADB=∠CBD,∴AD∥BC;
(2)连接CD,
∵AD∥BC,∴∠EDF=∠CBF,
∵,∴BC=CD,∴BF=DF,又∠DFE=∠BFC,
∴△DEF≌△BCF(ASA),∴DE=BC,
∴四边形BCDE是平行四边形,又BC=CD,
∴四边形BCDE是菱形.
24、如图,已知圆内接四边形ABDC中,∠BAC=60°,AB=AC,AD为它的对角线.
求证:AD=BD+CD.
【答案】见解析.
【解析】解:连接BC,
∠BAC=60°,AB=AC,
△ABC为等边三角形,
∠ABC=∠ACB=60°,
∠ADC=∠ABC
∠ADB=∠ACB
在AD上取点E、F,使DE=DB、DF=DC,连接BE、CF,
∴△BDE、△CDF为等边三角形,
∴∠DEB=∠DFC=60°,
∴∠AEB=∠CFA=120°,
又∠FAC+∠FCA=∠DFC=60°、∠FAC+∠EAB=∠BAC=60°,∴∠EAB=∠FCA,
在△ABE和△CAF中,∵
,∴△ABE≌△CAF(AAS),
∴AE=CF,
∴AD=DE+AE=BD+FC=BD+CD.
25、如图,在☉O中,P为的中点,弦AD,PC互相垂直,垂足为M,BC分别与AD,PD相交于点E,N,连接BD,MN.
(1)求证:N为BE的中点.
(2)若☉O的半径为8,的度数为90°,求线段MN的长.
解:(1)证明∵AD⊥PC,∴∠EMC=90°.
∵P为的中点,∴=,∴∠ADP=∠BCP.
∵∠CEM=∠DEN,∴∠DNE=∠EMC=90°=∠DNB.
∵=,∴∠BDP=∠ADP,
∴∠DEN=∠DBN,∴DE=DB,∴EN=BN,∴N为BE的中点.
(2)如图,连接OA,OB,AB,AC.
∵的度数为90°,∴∠AOB=90°.∵OA=OB=8,∴AB=8.
由(1)同理得AM=EM.∵EN=BN,∴MN是△AEB的中位线,
∴MN=AB=4.
26、△ABC中,AB=AC=5,BC=6,⊙O是△ABC的外接圆.
(1)如图①,求⊙O的半径;
(2)如图②,∠ABC的平分线交半径OA于点E,交⊙O于点D.求OE的长.
【分析】(1)过A点作AH⊥BC于H,如图①,利用等腰三角形的性质得BH=CH=3,根据垂径定理的推论可判断点O在AH上,则利用勾股定理可计算出AH=4,连接OB,设⊙O的半径为r,在Rt△OBH中利用勾股定理得到32+(4﹣r)2=r2,然后解方程即可;
(2)作EF⊥AB于F,如图,根据角平分线的性质得到EH=EF,利用面积法得到,所以EH=AH=,然后利用(1)得OH=,从而计算EH﹣OH得到OE的长.
【解析】(1)过A点作AH⊥BC于H,如图①,
∵AB=AC,∴BH=CH=BC=3,即AH垂直平分BC,∴点O在AH上,
在Rt△ABH中,AH==4,
连接OB,设⊙O的半径为r,则OB=r,OH=AH﹣OA=4﹣r,
在Rt△OBH中,32+(4﹣r)2=r2,解得r=,即⊙O的半径为;
(2)作EF⊥AB于F,如图,
∵BD平分∠ABC,∴EH=EF,
27、定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段
.
(2)在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由.友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
(3)如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由.若此时AB=3,BD=,求BC的长.
【解析】(1)只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.因此AC是该损矩形的直径;
(2)
作图如图;
∵点P为AC中点,∴PA=PC=AC.
∵∠ABC=∠ADC=90°,∴BP=DP=AC,∴PA=PB=PC=PD,
∴点A、B、C、D在以P为圆心,AC为半径的同一个圆上.
(3)∵菱形ACEF,∴∠ADC=90°,AE=2AD,FC=2CD,∴四边形ABCD为损矩形,
∴由(2)可知,点A、B、C、D在同一个圆上.
∵AM平分∠BAD,∴∠ABD=∠CBD=45°,∴AD=CD,∴四边形ACEF为正方形.
∵点BD平分∠ABC,BD=,∴点D到AB、BC的距离h为4,
∴=6.
,
,,
∵,∴+=6+2BC,
∴BC=5或BC=-3(舍去),
∴BC=5.
28、如图,等边三角形内接于,是上一动点,连接,,,延长到点,使,连接.
(1)求证:是等边三角形;
(2)填空:①若,,则的长为____________;
②当的度数为_________时,四边形为菱形.
【答案】(1)证明见解析;(2)①3;②30°.
【解析】(1)∵△ABC是等边三角形,∴AB=AC=BC,∠ABC=∠ACB=∠BAC=60°,
∵∠CBD与∠CAD是所对的圆周角,∴∠CBD=∠CAD,
同理可得:∠ABC=∠ADC=60°,
∵∠ACE=∠CAD+∠ADC,∴∠ACE=∠ABC+∠CBD=∠ABD,
在△ABD和△ACE中,,
∴△ABD≌△ACE,∴AD=AE,∴△ADE是等边三角形.
(2)①∵BD=CE=1,DE=CD+CE,CD=2,∴DE=3,
∵△ADE是等边三角形,∴AD=DE=3.
故答案为:3
②如图,连接OB、OC,
∵∠BAC和∠BOC分别是所对的圆周角和圆心角,∴∠BOC=2∠BAC=120°,
∵OB=OC,∴∠OCB=30°,
∵四边形为菱形,∴∠BCD=∠OCB=30°,
∵∠BAD和∠BCD都是所对的圆周角,∴∠BAD=∠BCD=30°,
∴当的度数为30°时,四边形为菱形.
故答案为:30°
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
