第十章概率单元基础试题-2020-2021学年高一数学人教A版必修第二册(Word含答案解析)
文档属性
| 名称 | 第十章概率单元基础试题-2020-2021学年高一数学人教A版必修第二册(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 853.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 09:08:32 | ||
图片预览




文档简介
高一第二学期数学第十章概率单元基础试题-2020-2021学年人教A版必修第二册
一、单选题
1.给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②“当x为某一实数时,可使x2≤0”是不可能事件;③“明天天津市要下雨”是必然事件;④“从100个灯泡(含有10个次品)中取出5个,5个全是次品”是随机事件.
其中正确命题的个数是(
)
A.0
B.1
C.2
D.3
2.抽查10件产品,设试验的样本空间为Ω,A=“至多有1件次品”,B=“至少有两件次品”,则(
)
A.A?B
B.B?A
C.A∩B≠?
D.A∩B=?,且A∪B=Ω
3.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马劣于齐王的上等马,优于齐王的中等马,田忌的中等马劣于齐王的中等马,优于齐王的下等马,田忌的下等马劣于齐王的下等马,现两人进行赛马比赛,比赛规则为:每匹马只能用一次,每场比赛双方各出一匹马,共比赛三场.每场比赛中胜者得1分,否则得0分.若每场比赛之前彼此都不知道对方所用之马,则比赛结束时,田忌得2分的概率为(
).
A.
B.
C.
D.
4.围棋盒子中有若干粒黑子和白子,从中任意取出2粒,2粒都是黑子的概率为,都是白子的概率为,则取出的2粒颜色不同的概率为(
)
A.
B.
C.
D.
5.某工厂生产了一批节能灯泡,这批产品按质量分为一等品、二等品、不合格品.从这批产品中随机抽取一件进行检测,设“抽到一等品”的概率为,“抽到二等品”的概率为,则“抽到不合格品”的概率为(
)
A.0.05
B.0.25
C.0.8
D.0.95
6.从数字中随机取两个不同的数,分别记为和,则为整数的概率是(
)
A.
B.
C.
D.
7.下列命题中正确的是(
)
A.事件发生的概率等于事件发生的频率
B.一个质地均匀的骰子掷一次得到3点的概率是,说明这个骰子掷6次一定会出现一次3点
C.掷两枚质地均匀的硬币,事件为“一枚正面朝上,一枚反面朝上”,事件为“两枚都是正面朝上”,则
D.对于两个事件、,若,则事件与事件互斥
8.某次战役中,狙击手A受命射击敌机,若要击落敌机,需命中机首2次或命中机中3次或命中机尾1次,已知A每次射击,命中机首、机中、机尾的概率分别为0.2、0.4、0.1,未命中敌机的概率为0.3,且各次射击相互独立.若A至多射击两次,则他能击落敌机的概率为
A.0.23
B.0.2
C.0.16
D.0.1
二、多选题
9.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以,和表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以表示由乙罐取出的球是红球的事件,则下列结论中正确的是(
)
A.
B.
C.事件与事件相互独立
D.,,是两两互斥的事件
10.下列对各事件发生的概率判断正确的是(
)
A.某学生在上学的路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,那么该生在上学路上到第3个路口首次遇到红灯的概率为
B.三人独立地破译一份密码,他们能单独译出的概率分别为,,,假设他们破译密码是彼此独立的,则此密码被破译的概率为
C.甲袋中有8个白球,4个红球,乙袋中有6个白球,6个红球,从每袋中各任取一个球,则取到同色球的概率为
D.设两个独立事件A和B都不发生的概率为,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率是
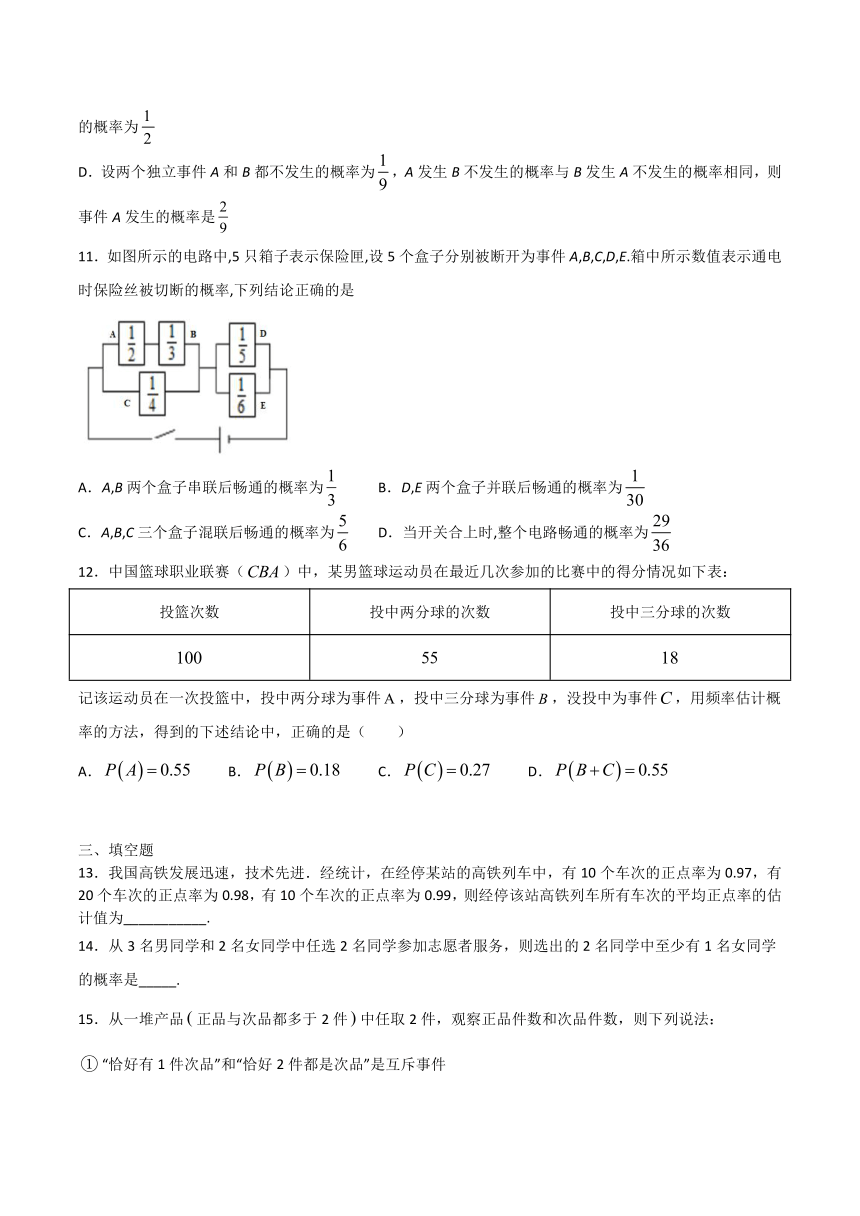
11.如图所示的电路中,5只箱子表示保险匣,设5个盒子分别被断开为事件A,B,C,D,E.箱中所示数值表示通电时保险丝被切断的概率,下列结论正确的是
A.A,B两个盒子串联后畅通的概率为
B.D,E两个盒子并联后畅通的概率为
C.A,B,C三个盒子混联后畅通的概率为
D.当开关合上时,整个电路畅通的概率为
12.中国篮球职业联赛()中,某男篮球运动员在最近几次参加的比赛中的得分情况如下表:
投篮次数
投中两分球的次数
投中三分球的次数
记该运动员在一次投篮中,投中两分球为事件,投中三分球为事件,没投中为事件,用频率估计概率的方法,得到的下述结论中,正确的是(
)
A.
B.
C.
D.
三、填空题
13.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
14.从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是_____.
15.从一堆产品正品与次品都多于2件中任取2件,观察正品件数和次品件数,则下列说法:
“恰好有1件次品”和“恰好2件都是次品”是互斥事件
“至少有1件正品”和“全是次品”是对立事件
“至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
“至少有1件次品”和“全是正品”是互斥事件也是对立事件
其中正确的有______填序号.
16.口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件“取出的两球同色”,“取出的2球中至少有一个黄球”,“取出的2球至少有一个白球”,“取出的两球不同色”,“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①与为对立事件;②与是互斥事件;③与是对立事件:④;⑤.
17.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为__________.
18.甲、乙两队进行篮球决赛,采取三场二胜制(当一队赢得二场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主客主”.设甲队主场取胜的概率为,客场取胜的概率为,且各场比赛结果相互独立,则甲队以获胜的概率是_____.
四、解答题
19.
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
20.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布直方图中的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率.
21.自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加
不准备参加
待定
男生
30
6
15
女生
15
9
25
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
22.中国共产党第十九次全国代表大会简称党的“十九大”在北京召开一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在内,按成绩分成5组:第1组,第2组,第3组,第4组,第5组,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
求这100人的平均得分同一组数据用该区间的中点值作代表;
求第3,4,5组分别选取的作深入学习的人数;
若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
23.电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型
第一类
第二类
第三类
第四类
第五类
第六类
电影部数
好评率
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加,哪类电影的好评率减少,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
参考答案
1.C
对于①,三个球全部放入两个盒子,有两种情况:1+2和3+0,故必有一个盒子有一个以上的球,所以该事件是必然事件,①正确;
对于②,x=0时x2=0,所以该事件不是不可能事件,②错误;
对于③,“明天天津市要下雨”是偶然事件,所以该事件是随机事件,③错误;
对于④,“从100个灯泡(含有10个次品)中取出5个,5个全是次品”,发生与否是随机的,所以该事件是随机事件,④正确.故正确命题有2个.
故选:C.
2.D
A=“至多有1件次品”,包含:0件次品和1件次品;
B=“至少有两件次品”包含:2件次品、3件次品、4件次品、5件次品、6件次品、7件次品、8件次品、9件次品和10件次品、
故A∩B=?,且A∪B=Ω.
故选:D
3.C
设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,双方各出上、中、下等马各1匹分组分别进行1场比赛,
所有的可能为:
Aa,Bb,Cc,田忌得0分;
Aa,Bc,Cb,田忌得1分
Ba,Ab,Cc,田忌得1分
Ba,Ac,Cb,田忌得1分;
Ca,Ab,Bc,田忌得2分,
Ca,Ac,Bb,田忌得1分
田忌得2分概率为,
故选:C
4.D
2粒都是黑子或2粒都是白子的概率为,
取出的2粒颜色不同的概率为.
故选:D.
5.A
“抽到一等品”与“抽到二等品”是互斥事件,
所以“抽到一等品或二等品”的概率为,
“抽到不合格品”与“抽到一等品或二等品”是对立事件,
故其概率为.
故选:A.
6.B
解:从数字中随机取两个不同的数,
则有种选法,有种选法,共有种情况;
则满足为整数的情况如下:
当时,或有种情况;
当时,有种情况;
当或时,则不可能为整数,
故共有种情况,
故为整数的概率是:.
故选:B.
7.C
解:对于A选项,频率与实验次数有关,且在概率附近摆动,故A选项错误;
对于B选项,根据概率的意义,一个质地均匀的骰子掷一次得到3点的概率是,表示一次实验发生的可能性是,故骰子掷6次出现3点的次数也不确定,故B选项错误;
对于C选项,根据概率的计算公式得,,故,故C选项正确;
对于D选项,设,A事件表示从中任取一个数,使得的事件,则,B事件表示从中任取一个数,使得的事件,则,显然,此时A事件与B事件不互斥,故D选项错误.
8.A
每次射击,命中机首、机中、机尾的概率分别为,未命中敌机的概率为,且各次射击相互独立,若射击一次就击落敌机,则他击中利敌机的机尾,故概率为;若射击次就击落敌机,则他次都击中利敌机的机首,概率为;或者第一次没有击中机尾、且第二次击中了机尾,概率为
,若至多射击两次,则他能击落敌机的概率为
,故选.
9.BD
因为每次取一球,所以,,是两两互斥的事件,故D正确;
因为,
所以,故B正确;
同理,
所以,故AC错误;
故选:BD
10.AC
对于A,该生在第3个路口首次遇到红灯的情况为前2个路口不是红灯,第3个路口是红灯,所以概率为,故A正确;
对于B,用A、B、C分別表示甲、乙、丙三人能破译出密码,则,,,“三个人都不能破译出密码”发生的概率为,所以此密码被破译的概率为,故B不正确;
对于C,设“从甲袋中取到白球”为事件A,则,设“从乙袋中取到白球”为事件B,则,故取到同色球的概率为,故C正确;
对于D,易得,即,
即,∴,又,
∴,∴,故D错误
故选AC
11.ACD
由题意知,,,,,,所以A,B两个盒子畅通的概率为,因此A正确;D,E两个盒子并联后畅通的概率为,因此B错误;A,B,C三个盘子混联后畅通的概率为,C正确;根据上述分析可知,当开关合上时,电路畅通的概率为,D正确.
故选:ACD
12.ABC
由题意可知,,,
事件与事件为对立事件,且事件、、互斥,
,.
故选:ABC.
13.0.98.
由题意得,经停该高铁站的列车正点数约为,其中高铁个数为10+20+10=40,所以该站所有高铁平均正点率约为.
14..
从3名男同学和2名女同学中任选2名同学参加志愿服务,共有种情况.
若选出的2名学生恰有1名女生,有种情况,
若选出的2名学生都是女生,有种情况,
所以所求的概率为.
15.
“恰好有1件次品”和“恰好2件都是次品”不能同时发生,是互斥事件,故正确;
“至少有1件正品”和“全是次品”,不能同时发生,是互斥事件也是对立事件,故正确;
“至少有1件正品”和“至少有1件次品”存在恰有一件正品和一件次品,
不是互斥事件但不是对立事件,故不正确;
“至少有1件次品”和“全是正品”不能同时发生,是互斥事件也是对立事件,正确.
故答案为.
16.①④
口袋里装有1红,2白,3黄共6个形状相同小球,从中取出2球,
事件
“取出的两球同色”,
“取出的2球中至少有一个黄球”,
“取出的2球至少有一个白球”,
“取出的两球不同色”,
“取出的2球中至多有一个白球”,
①,由对立事件定义得与为对立事件,故①正确;
②,与有可能同时发生,故与不是互斥事件,故②错误;
③,与有可能同时发生,不是对立事件,故③错误;
④,(C),(E),,
从而(C)(E),故④正确;
⑤,,从而(B)(C),故⑤错误.
故答案为:①④.
17..
解:由题意可知了,比赛可能的方法有种,
其中田忌可获胜的比赛方法有三种:田忌的中等马对齐王的下等马,
田忌的上等马对齐王的下等马,田忌的上等马对齐王的中等马,
结合古典概型公式可得,田忌的马获胜的概率为.
点睛:有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举.(2)注意区分排列与组合,以及计数原理的正确使用.
18.
甲队的主客场安排依次为“主客主”.
设甲队主场取胜的概率为,客场取胜的概率为,且各场比赛结果相互独立,
甲队以获胜的是指甲队前两场比赛中一胜一负,第三场比赛甲胜,
则甲队以获胜的概率是:.
故答案为:.
19.(1);(2)0.1
(1)由题意可知,所包含的事件为“甲连赢两球或乙连赢两球”
所以
(2)由题意可知,包含的事件为“前两球甲乙各得分,后两球均为甲得分”
所以
20.(1)0.006;(2);(3).
(1)因为,
所以
(2)由所给频率分布直方图知,50名受访职工评分不低于80的频率为,
所以该企业职工对该部门评分不低于80的概率的估计值为
(3)受访职工评分在[50,60)的有:50×0.006×10=3(人),
即为;
受访职工评分在[40,50)的有:
50×0.004×10=2(人),即为.
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是
又因为所抽取2人的评分都在[40,50)的结果有1种,即,
故所求的概率为
21.
解:
(1)分层抽样时的抽样比为=0.2,所以,在“准备参加”的同学中应抽取(30+15)×0.2=9(人),在“不准备参加”的同学中应抽取(6+9)×0.2=3(人),在“待定”的同学中应抽取(15+25)×0.2=8(人).
(2)在“准备参加”的同学中用分层抽样方法抽取6人,
则男生抽4人,女生抽2人,男生4人分别记作1,2,3,4,女生2人分别记作5,6.
从6人中任取2人共有以下15种情况:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),
(5,6).
其中至少有一名女生的情况共有9种:(1,5),(1,6),(2,5),(2,6),(3,5),(3,6),(4,5),(4,6),(5,6).
所以,至少有一名女生的概率P==0.6.
22.这100人的平均得分为:
.
第3组的人数为,
第4组的人数为,
第5组的人数为,故共有60人,
用分层抽样在这三个组选取的人数分别为:3,2,
记其他人为甲、乙、丙、丁、戊、己,
则所有选取的结果为甲、乙、甲、丙、甲、丁、甲、戊、甲、己、
乙、丙、乙、丁、乙、戊、乙、己?、丙、丁、丙、戊、丙、己、
丁、戊、丁、己?、戊、己共15种情况,
其中甲、乙、丙这3人至多有一人被选取有12种情况,
故甲、乙、丙这3人至多有一人被选取的概率为
23.
(Ⅰ)由题意知,样本中电影的总部数是,
第四类电影中获得好评的电影部数是,
故所求概率为;
(Ⅱ)设“随机选取部电影,这部电影没有获得好评”为事件B.
没有获得好评的电影共有部,
由古典概型概率公式得;
(Ⅲ)增加第五类电影的好评率,
减少第二类电影的好评率.
试卷第1页,总3页
一、单选题
1.给出下列四个命题:
①“三个球全部放入两个盒子,其中必有一个盒子有一个以上的球”是必然事件;②“当x为某一实数时,可使x2≤0”是不可能事件;③“明天天津市要下雨”是必然事件;④“从100个灯泡(含有10个次品)中取出5个,5个全是次品”是随机事件.
其中正确命题的个数是(
)
A.0
B.1
C.2
D.3
2.抽查10件产品,设试验的样本空间为Ω,A=“至多有1件次品”,B=“至少有两件次品”,则(
)
A.A?B
B.B?A
C.A∩B≠?
D.A∩B=?,且A∪B=Ω
3.《史记》卷六十五《孙子吴起列传第五》中有这样一道题:齐王与田忌赛马,田忌的上等马劣于齐王的上等马,优于齐王的中等马,田忌的中等马劣于齐王的中等马,优于齐王的下等马,田忌的下等马劣于齐王的下等马,现两人进行赛马比赛,比赛规则为:每匹马只能用一次,每场比赛双方各出一匹马,共比赛三场.每场比赛中胜者得1分,否则得0分.若每场比赛之前彼此都不知道对方所用之马,则比赛结束时,田忌得2分的概率为(
).
A.
B.
C.
D.
4.围棋盒子中有若干粒黑子和白子,从中任意取出2粒,2粒都是黑子的概率为,都是白子的概率为,则取出的2粒颜色不同的概率为(
)
A.
B.
C.
D.
5.某工厂生产了一批节能灯泡,这批产品按质量分为一等品、二等品、不合格品.从这批产品中随机抽取一件进行检测,设“抽到一等品”的概率为,“抽到二等品”的概率为,则“抽到不合格品”的概率为(
)
A.0.05
B.0.25
C.0.8
D.0.95
6.从数字中随机取两个不同的数,分别记为和,则为整数的概率是(
)
A.
B.
C.
D.
7.下列命题中正确的是(
)
A.事件发生的概率等于事件发生的频率
B.一个质地均匀的骰子掷一次得到3点的概率是,说明这个骰子掷6次一定会出现一次3点
C.掷两枚质地均匀的硬币,事件为“一枚正面朝上,一枚反面朝上”,事件为“两枚都是正面朝上”,则
D.对于两个事件、,若,则事件与事件互斥
8.某次战役中,狙击手A受命射击敌机,若要击落敌机,需命中机首2次或命中机中3次或命中机尾1次,已知A每次射击,命中机首、机中、机尾的概率分别为0.2、0.4、0.1,未命中敌机的概率为0.3,且各次射击相互独立.若A至多射击两次,则他能击落敌机的概率为
A.0.23
B.0.2
C.0.16
D.0.1
二、多选题
9.甲罐中有5个红球,2个白球和3个黑球,乙罐中有4个红球,3个白球和3个黑球.先从甲罐中随机取出一球放入乙罐,分别以,和表示由甲罐取出的球是红球,白球和黑球的事件;再从乙罐中随机取出一球,以表示由乙罐取出的球是红球的事件,则下列结论中正确的是(
)
A.
B.
C.事件与事件相互独立
D.,,是两两互斥的事件
10.下列对各事件发生的概率判断正确的是(
)
A.某学生在上学的路上要经过4个路口,假设在各路口是否遇到红灯是相互独立的,遇到红灯的概率都是,那么该生在上学路上到第3个路口首次遇到红灯的概率为
B.三人独立地破译一份密码,他们能单独译出的概率分别为,,,假设他们破译密码是彼此独立的,则此密码被破译的概率为
C.甲袋中有8个白球,4个红球,乙袋中有6个白球,6个红球,从每袋中各任取一个球,则取到同色球的概率为
D.设两个独立事件A和B都不发生的概率为,A发生B不发生的概率与B发生A不发生的概率相同,则事件A发生的概率是
11.如图所示的电路中,5只箱子表示保险匣,设5个盒子分别被断开为事件A,B,C,D,E.箱中所示数值表示通电时保险丝被切断的概率,下列结论正确的是
A.A,B两个盒子串联后畅通的概率为
B.D,E两个盒子并联后畅通的概率为
C.A,B,C三个盒子混联后畅通的概率为
D.当开关合上时,整个电路畅通的概率为
12.中国篮球职业联赛()中,某男篮球运动员在最近几次参加的比赛中的得分情况如下表:
投篮次数
投中两分球的次数
投中三分球的次数
记该运动员在一次投篮中,投中两分球为事件,投中三分球为事件,没投中为事件,用频率估计概率的方法,得到的下述结论中,正确的是(
)
A.
B.
C.
D.
三、填空题
13.我国高铁发展迅速,技术先进.经统计,在经停某站的高铁列车中,有10个车次的正点率为0.97,有20个车次的正点率为0.98,有10个车次的正点率为0.99,则经停该站高铁列车所有车次的平均正点率的估计值为___________.
14.从3名男同学和2名女同学中任选2名同学参加志愿者服务,则选出的2名同学中至少有1名女同学的概率是_____.
15.从一堆产品正品与次品都多于2件中任取2件,观察正品件数和次品件数,则下列说法:
“恰好有1件次品”和“恰好2件都是次品”是互斥事件
“至少有1件正品”和“全是次品”是对立事件
“至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
“至少有1件次品”和“全是正品”是互斥事件也是对立事件
其中正确的有______填序号.
16.口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件“取出的两球同色”,“取出的2球中至少有一个黄球”,“取出的2球至少有一个白球”,“取出的两球不同色”,“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①与为对立事件;②与是互斥事件;③与是对立事件:④;⑤.
17.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马,田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为__________.
18.甲、乙两队进行篮球决赛,采取三场二胜制(当一队赢得二场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主客主”.设甲队主场取胜的概率为,客场取胜的概率为,且各场比赛结果相互独立,则甲队以获胜的概率是_____.
四、解答题
19.
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
20.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
(1)求频率分布直方图中的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在的受访职工中,随机抽取2人,求此2人评分都在的概率.
21.自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加
不准备参加
待定
男生
30
6
15
女生
15
9
25
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.
22.中国共产党第十九次全国代表大会简称党的“十九大”在北京召开一段时间后,某单位就“十九大”精神的领会程度随机抽取100名员工进行问卷调查,调查问卷共有20个问题,每个问题5分,调查结束后,发现这100名员工的成绩都在内,按成绩分成5组:第1组,第2组,第3组,第4组,第5组,绘制成如图所示的频率分布直方图,已知甲、乙、丙分别在第3,4,5组,现在用分层抽样的方法在第3,4,5组共选取6人对“十九大”精神作深入学习.
求这100人的平均得分同一组数据用该区间的中点值作代表;
求第3,4,5组分别选取的作深入学习的人数;
若甲、乙、丙都被选取对“十九大”精神作深入学习,之后要从这6人随机选取2人再全面考查他们对“十九大”精神的领会程度,求甲、乙、丙这3人至多有一人被选取的概率.
23.电影公司随机收集了电影的有关数据,经分类整理得到下表:
电影类型
第一类
第二类
第三类
第四类
第五类
第六类
电影部数
好评率
好评率是指:一类电影中获得好评的部数与该类电影的部数的比值.
(Ⅰ)从电影公司收集的电影中随机选取部,求这部电影是获得好评的第四类电影的概率;
(Ⅱ)随机选取部电影,估计这部电影没有获得好评的概率;
(Ⅲ)电影公司为增加投资回报,拟改变投资策略,这将导致不同类型电影的好评率发生变化.假设表格中只有两类电影的好评率数据发生变化,那么哪类电影的好评率增加,哪类电影的好评率减少,使得获得好评的电影总部数与样本中的电影总部数的比值达到最大?(只需写出结论)
参考答案
1.C
对于①,三个球全部放入两个盒子,有两种情况:1+2和3+0,故必有一个盒子有一个以上的球,所以该事件是必然事件,①正确;
对于②,x=0时x2=0,所以该事件不是不可能事件,②错误;
对于③,“明天天津市要下雨”是偶然事件,所以该事件是随机事件,③错误;
对于④,“从100个灯泡(含有10个次品)中取出5个,5个全是次品”,发生与否是随机的,所以该事件是随机事件,④正确.故正确命题有2个.
故选:C.
2.D
A=“至多有1件次品”,包含:0件次品和1件次品;
B=“至少有两件次品”包含:2件次品、3件次品、4件次品、5件次品、6件次品、7件次品、8件次品、9件次品和10件次品、
故A∩B=?,且A∪B=Ω.
故选:D
3.C
设齐王的上,中,下三个等次的马分别为a,b,c,田忌的上,中,下三个等次的马分别为记为A,B,C,双方各出上、中、下等马各1匹分组分别进行1场比赛,
所有的可能为:
Aa,Bb,Cc,田忌得0分;
Aa,Bc,Cb,田忌得1分
Ba,Ab,Cc,田忌得1分
Ba,Ac,Cb,田忌得1分;
Ca,Ab,Bc,田忌得2分,
Ca,Ac,Bb,田忌得1分
田忌得2分概率为,
故选:C
4.D
2粒都是黑子或2粒都是白子的概率为,
取出的2粒颜色不同的概率为.
故选:D.
5.A
“抽到一等品”与“抽到二等品”是互斥事件,
所以“抽到一等品或二等品”的概率为,
“抽到不合格品”与“抽到一等品或二等品”是对立事件,
故其概率为.
故选:A.
6.B
解:从数字中随机取两个不同的数,
则有种选法,有种选法,共有种情况;
则满足为整数的情况如下:
当时,或有种情况;
当时,有种情况;
当或时,则不可能为整数,
故共有种情况,
故为整数的概率是:.
故选:B.
7.C
解:对于A选项,频率与实验次数有关,且在概率附近摆动,故A选项错误;
对于B选项,根据概率的意义,一个质地均匀的骰子掷一次得到3点的概率是,表示一次实验发生的可能性是,故骰子掷6次出现3点的次数也不确定,故B选项错误;
对于C选项,根据概率的计算公式得,,故,故C选项正确;
对于D选项,设,A事件表示从中任取一个数,使得的事件,则,B事件表示从中任取一个数,使得的事件,则,显然,此时A事件与B事件不互斥,故D选项错误.
8.A
每次射击,命中机首、机中、机尾的概率分别为,未命中敌机的概率为,且各次射击相互独立,若射击一次就击落敌机,则他击中利敌机的机尾,故概率为;若射击次就击落敌机,则他次都击中利敌机的机首,概率为;或者第一次没有击中机尾、且第二次击中了机尾,概率为
,若至多射击两次,则他能击落敌机的概率为
,故选.
9.BD
因为每次取一球,所以,,是两两互斥的事件,故D正确;
因为,
所以,故B正确;
同理,
所以,故AC错误;
故选:BD
10.AC
对于A,该生在第3个路口首次遇到红灯的情况为前2个路口不是红灯,第3个路口是红灯,所以概率为,故A正确;
对于B,用A、B、C分別表示甲、乙、丙三人能破译出密码,则,,,“三个人都不能破译出密码”发生的概率为,所以此密码被破译的概率为,故B不正确;
对于C,设“从甲袋中取到白球”为事件A,则,设“从乙袋中取到白球”为事件B,则,故取到同色球的概率为,故C正确;
对于D,易得,即,
即,∴,又,
∴,∴,故D错误
故选AC
11.ACD
由题意知,,,,,,所以A,B两个盒子畅通的概率为,因此A正确;D,E两个盒子并联后畅通的概率为,因此B错误;A,B,C三个盘子混联后畅通的概率为,C正确;根据上述分析可知,当开关合上时,电路畅通的概率为,D正确.
故选:ACD
12.ABC
由题意可知,,,
事件与事件为对立事件,且事件、、互斥,
,.
故选:ABC.
13.0.98.
由题意得,经停该高铁站的列车正点数约为,其中高铁个数为10+20+10=40,所以该站所有高铁平均正点率约为.
14..
从3名男同学和2名女同学中任选2名同学参加志愿服务,共有种情况.
若选出的2名学生恰有1名女生,有种情况,
若选出的2名学生都是女生,有种情况,
所以所求的概率为.
15.
“恰好有1件次品”和“恰好2件都是次品”不能同时发生,是互斥事件,故正确;
“至少有1件正品”和“全是次品”,不能同时发生,是互斥事件也是对立事件,故正确;
“至少有1件正品”和“至少有1件次品”存在恰有一件正品和一件次品,
不是互斥事件但不是对立事件,故不正确;
“至少有1件次品”和“全是正品”不能同时发生,是互斥事件也是对立事件,正确.
故答案为.
16.①④
口袋里装有1红,2白,3黄共6个形状相同小球,从中取出2球,
事件
“取出的两球同色”,
“取出的2球中至少有一个黄球”,
“取出的2球至少有一个白球”,
“取出的两球不同色”,
“取出的2球中至多有一个白球”,
①,由对立事件定义得与为对立事件,故①正确;
②,与有可能同时发生,故与不是互斥事件,故②错误;
③,与有可能同时发生,不是对立事件,故③错误;
④,(C),(E),,
从而(C)(E),故④正确;
⑤,,从而(B)(C),故⑤错误.
故答案为:①④.
17..
解:由题意可知了,比赛可能的方法有种,
其中田忌可获胜的比赛方法有三种:田忌的中等马对齐王的下等马,
田忌的上等马对齐王的下等马,田忌的上等马对齐王的中等马,
结合古典概型公式可得,田忌的马获胜的概率为.
点睛:有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏,可借助“树状图”列举.(2)注意区分排列与组合,以及计数原理的正确使用.
18.
甲队的主客场安排依次为“主客主”.
设甲队主场取胜的概率为,客场取胜的概率为,且各场比赛结果相互独立,
甲队以获胜的是指甲队前两场比赛中一胜一负,第三场比赛甲胜,
则甲队以获胜的概率是:.
故答案为:.
19.(1);(2)0.1
(1)由题意可知,所包含的事件为“甲连赢两球或乙连赢两球”
所以
(2)由题意可知,包含的事件为“前两球甲乙各得分,后两球均为甲得分”
所以
20.(1)0.006;(2);(3).
(1)因为,
所以
(2)由所给频率分布直方图知,50名受访职工评分不低于80的频率为,
所以该企业职工对该部门评分不低于80的概率的估计值为
(3)受访职工评分在[50,60)的有:50×0.006×10=3(人),
即为;
受访职工评分在[40,50)的有:
50×0.004×10=2(人),即为.
从这5名受访职工中随机抽取2人,所有可能的结果共有10种,它们是
又因为所抽取2人的评分都在[40,50)的结果有1种,即,
故所求的概率为
21.
解:
(1)分层抽样时的抽样比为=0.2,所以,在“准备参加”的同学中应抽取(30+15)×0.2=9(人),在“不准备参加”的同学中应抽取(6+9)×0.2=3(人),在“待定”的同学中应抽取(15+25)×0.2=8(人).
(2)在“准备参加”的同学中用分层抽样方法抽取6人,
则男生抽4人,女生抽2人,男生4人分别记作1,2,3,4,女生2人分别记作5,6.
从6人中任取2人共有以下15种情况:
(1,2),(1,3),(1,4),(1,5),(1,6),
(2,3),(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6),
(4,5),(4,6),
(5,6).
其中至少有一名女生的情况共有9种:(1,5),(1,6),(2,5),(2,6),(3,5),(3,6),(4,5),(4,6),(5,6).
所以,至少有一名女生的概率P==0.6.
22.这100人的平均得分为:
.
第3组的人数为,
第4组的人数为,
第5组的人数为,故共有60人,
用分层抽样在这三个组选取的人数分别为:3,2,
记其他人为甲、乙、丙、丁、戊、己,
则所有选取的结果为甲、乙、甲、丙、甲、丁、甲、戊、甲、己、
乙、丙、乙、丁、乙、戊、乙、己?、丙、丁、丙、戊、丙、己、
丁、戊、丁、己?、戊、己共15种情况,
其中甲、乙、丙这3人至多有一人被选取有12种情况,
故甲、乙、丙这3人至多有一人被选取的概率为
23.
(Ⅰ)由题意知,样本中电影的总部数是,
第四类电影中获得好评的电影部数是,
故所求概率为;
(Ⅱ)设“随机选取部电影,这部电影没有获得好评”为事件B.
没有获得好评的电影共有部,
由古典概型概率公式得;
(Ⅲ)增加第五类电影的好评率,
减少第二类电影的好评率.
试卷第1页,总3页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
