2020-2021学年高一下学期数学人教A版必修第二册第九章 统计 单元测试(含答案)
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版必修第二册第九章 统计 单元测试(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 00:00:00 | ||
图片预览


文档简介
人教版必修第二册2020-2021年高一数学下册第九章《统计》单元卷
一、单选题
1.某中学有300名教师,其中初级教师60名,中级教师150名,高级教师90名.考虑采用分层抽样或系统抽样方法,从全校教师中抽取10人参加一个网络教学座谈会.采用分层抽样时,将初级教师随机编号为1~60,中级教师随机编号为61~210,高级教师随机编号为211~300;采用系统抽样时,将全校教师统一随机编号为1,2,…,300,并将整个编号从小到大依次均分为10组.
给出下列两组样本号码:①7,34,61,88,115,142,169,223,250,288;②26,32,90,100,138,172,188,211,254,297.
则下列结论中错误的是(
)
A.样本①可能为分层抽样
B.样本②可能为分层抽样
C.样本①可能为系统抽样
D.样本②可能为系统抽样
2.总体由编号为的个个体组成,利用随机数表从中抽取个个体,下面提供随机数表的第行到第行:
若从表中第行第列开始向右依次读取,则抽取的第个个体的编号是(
)
A.
B.
C.
D.
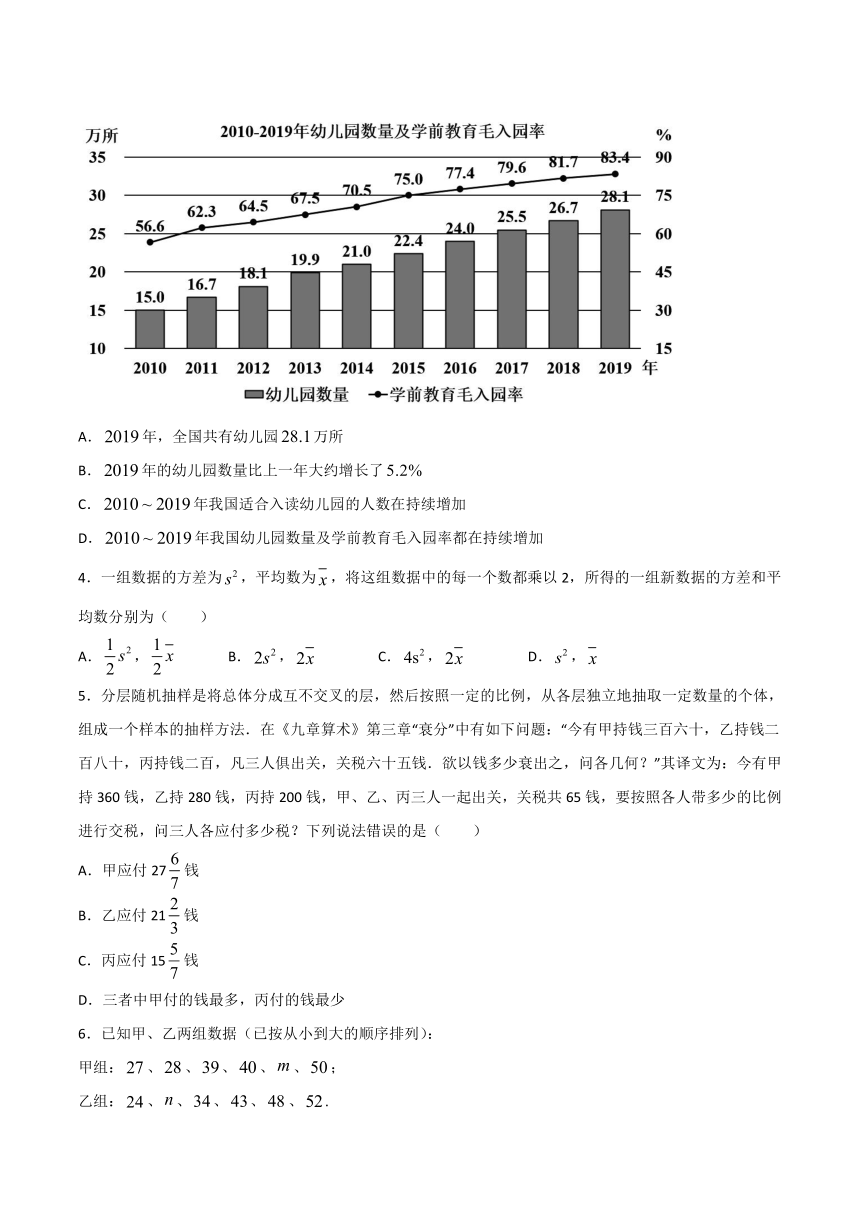
3.近年来,我国继续大力发展公办幼儿园,积极扶持普惠性民办幼儿园,使得普惠性学前教育资源迅速增加.如图为国家统计局发布的年幼儿园数量及学前教育毛入园率统计图.根据该统计图,下列说法不一定正确的是(
)
注:
.
A.年,全国共有幼儿园万所
B.年的幼儿园数量比上一年大约增长了
C.年我国适合入读幼儿园的人数在持续增加
D.年我国幼儿园数量及学前教育毛入园率都在持续增加
4.一组数据的方差为,平均数为,将这组数据中的每一个数都乘以2,所得的一组新数据的方差和平均数分别为(
)
A.,
B.,
C.,
D.,
5.分层随机抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱三百六十,乙持钱二百八十,丙持钱二百,凡三人俱出关,关税六十五钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持360钱,乙持280钱,丙持200钱,甲、乙、丙三人一起出关,关税共65钱,要按照各人带多少的比例进行交税,问三人各应付多少税?下列说法错误的是(
)
A.甲应付27钱
B.乙应付21钱
C.丙应付15钱
D.三者中甲付的钱最多,丙付的钱最少
6.已知甲、乙两组数据(已按从小到大的顺序排列):
甲组:、、、、、;
乙组:、、、、、.
若这两组数据的百分位数、百分位数分别相等,则等于(
)
A.
B.
C.
D.
7.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为(
)
A.40
B.39
C.38
D.37
8.某高中为了解学生课外知识的积累情况,随机抽取名同学参加课外知识测试,测试共道题,每答对一题得分,答错得分.已知每名同学至少能答对道题,得分不少于分记为及格,不少于分记为优秀,测试成绩百分比分布图如图所示,则下列说法正确的是(
)
A.该次课外知识测试及格率为
B.该次课外知识测试得满分的同学有名
C.该次测试成绩的中位数大于测试成绩的平均数
D.若该校共有名学生,则课外知识测试成绩能得优秀的同学大约有名
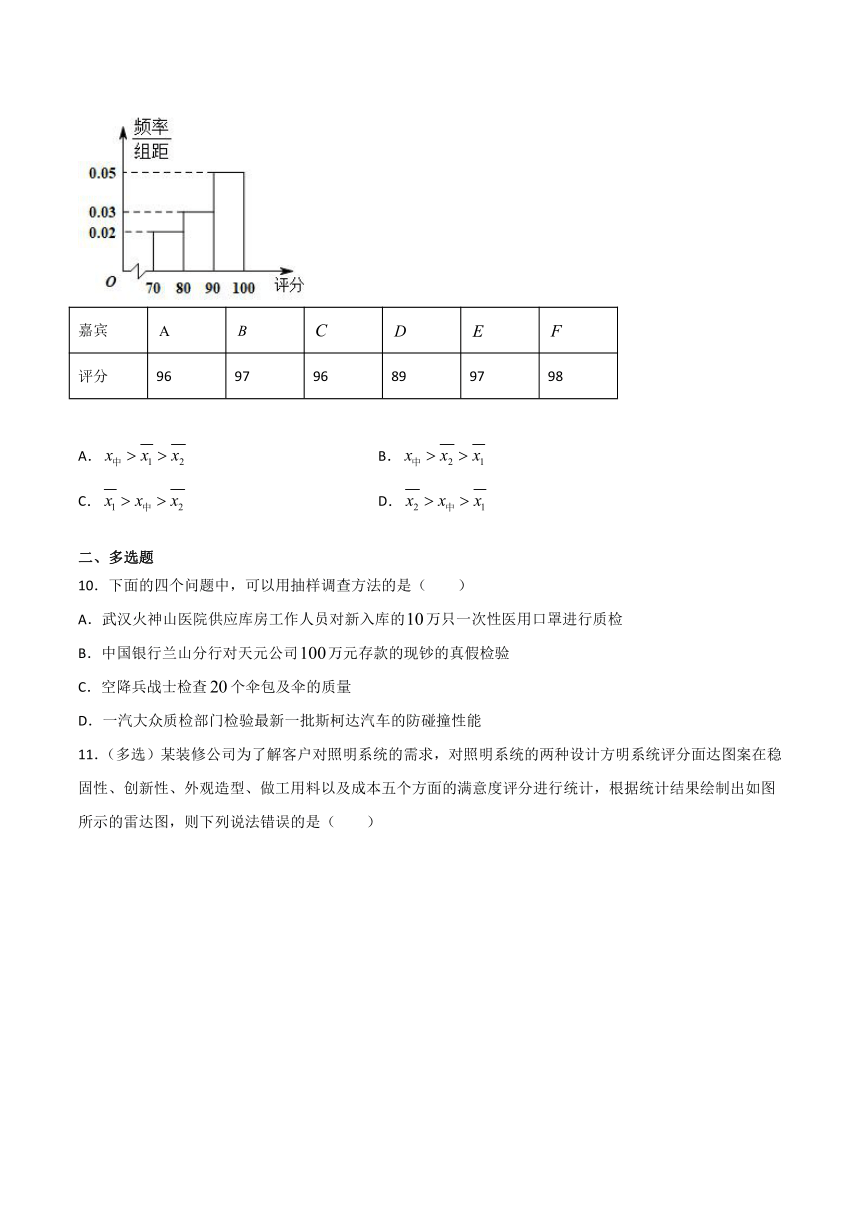
9.“脱口秀大赛”上选手的分数分为观众评分和嘉宾评分.组织方将观众评分按照,,分组,绘制频率分布直方图如图所示.嘉宾评分的平均数为,观众评分的平均数为,中位数为,则下列选项正确的是(
)
嘉宾
评分
96
97
96
89
97
98
A.
B.
C.
D.
二、多选题
10.下面的四个问题中,可以用抽样调查方法的是(
)
A.武汉火神山医院供应库房工作人员对新入库的万只一次性医用口罩进行质检
B.中国银行兰山分行对天元公司万元存款的现钞的真假检验
C.空降兵战士检查个伞包及伞的质量
D.一汽大众质检部门检验最新一批斯柯达汽车的防碰撞性能
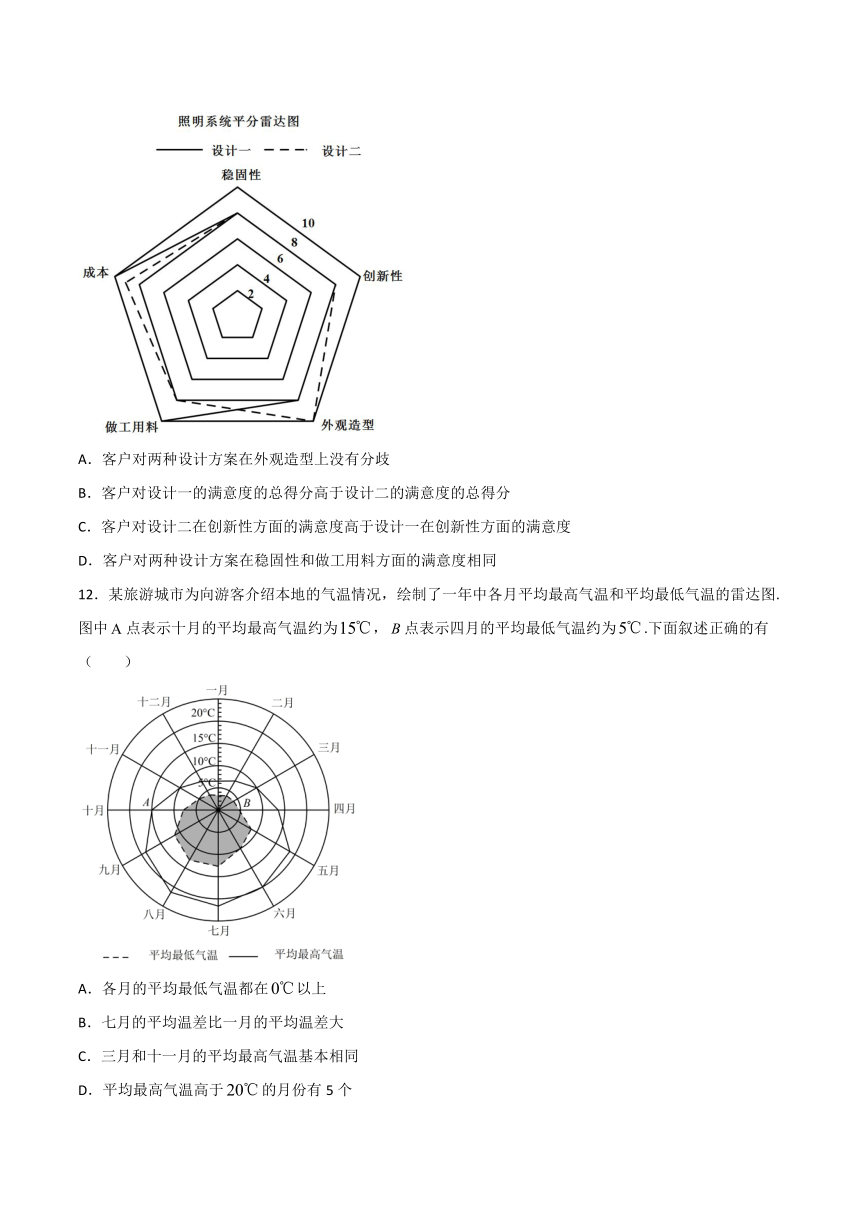
11.(多选)某装修公司为了解客户对照明系统的需求,对照明系统的两种设计方明系统评分面达图案在稳固性、创新性、外观造型、做工用料以及成本五个方面的满意度评分进行统计,根据统计结果绘制出如图所示的雷达图,则下列说法错误的是(
)
A.客户对两种设计方案在外观造型上没有分歧
B.客户对设计一的满意度的总得分高于设计二的满意度的总得分
C.客户对设计二在创新性方面的满意度高于设计一在创新性方面的满意度
D.客户对两种设计方案在稳固性和做工用料方面的满意度相同
12.某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中点表示十月的平均最高气温约为,点表示四月的平均最低气温约为.下面叙述正确的有(
)
A.各月的平均最低气温都在以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于的月份有5个
三、填空题
13.某林场新种了一批树苗,其中杉树苗棵,树苗棵.为调查树苗的生长情况,按树苗的种类采用分层抽样的方法从中抽取样本.若样本中松树苗有棵,则杉树苗的棵数为________.
14.如图所示是一个样本容量为100的频率分布直方图,则由图形中的数据,可知其25%分位数为____________.
15.已知某篮球运动员在最近5场比赛中的得分的折线图如图所示,则该运动员得分的标准差为__________.
16.某高中针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级
高二年级
高三年级
泥塑
a
b
c
剪纸
x
y
z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取________人.
17.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
四、解答题
18.某地区拟举办汉字听写大赛,某校为了选拔优秀的学生参加比赛,在本校举行了次汉字听写大赛,其中甲、乙两位同学的成绩最优异,由甲、乙两位同学的成绩绘制的茎叶图如图所示.已知甲成绩的中位数小于乙成绩的中位数.
(1)求的值;
(2)若要从甲、乙中选择一名同学参加该地区举办的汉字听写大赛,试从统计学的角度分析,选哪位同学比较合适.
19.年,面对突如其来的新冠肺炎疫情冲击,在党中央领导下,各地区各部门统筹疫情防控和经济社会发展取得显著成效,商业模式创新发展,消费结构升级持续发展.某主打线上零售产品的企业随机抽取了名销售员,统计了其年的月均销售额(单位:万元),将数据按照分成组,制成了如图所示的频率分布直方图.已知组的频数比组多.
(1)求频率分布直方图中和的值;
(2)该企业为了挖掘销售员的工作潜力,对销售员实行冲刺目标管理,即给销售员确定一个具体的冲刺目标,完成这个冲刺目标,则给予额外的奖励,若公司希望恰有的销售人员能够获得额外奖励,求该企业应该制定的月销售冲刺目标值.
20.某网络营销部门随机抽查了某市200名网友在2019年11月11日的网购金额,所得数据如下表:
网购金额(单位:千元)
人数
频率
[0,1)
16
0.08
[1,2)
24
0.12
[2,3)
x
p
[3,4)
y
q
[4,5)
16
0.08
[5,6]
14
0.07
合计
200
1.00
已知网购金额低于3千元与不低于3千元的人数比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率直方图;
(2)估计网购金额的25百分位数(结果保留3位有效数字).
21.某家水果店的店长为了解本店苹果的日销售情况,记录了近期连续120天苹果的日销售量(单位:),并绘制频率分布直方图如下:
(1)请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数;(同一组中的数据以这组数据所在区间中点的值作代表)
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在10天中,大约有8天可以满足顾客的需求).请问每天应该进多少千克苹果?(精确到整数位)
22.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成两组,每组100只,其中给A组小鼠服用甲离子溶液,给B组小鼠服用乙离子溶液,给每组小鼠服用的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到的估计值为0.70.
(1)求乙离子残留百分比直方图中的值;
(2)估计甲离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
(3)估计乙离子残留百分比的中位数.(保留2位有效数字)
参考答案
1.C
若采用分层抽样,则抽样比例为,
从而初,中,高级教师抽取的人数分别为2,5,3,
所以在编号1~60内抽取2个号码,在编号61~210内抽取5个号码,
在编号211~300内抽取3个号码,样本①,②都符合.
若采用系统抽样,则每30个编号抽取1个号码,
即在编号1~30,31~60,61~90,…,271~300内各抽取1个号码.
因为61,88都在编号61~90范围内,则样本①不符合,
但样本②符合,
2.B
利用随机数表从第行第列开始向右读取,依次为09,84(去除),96(去除),57(去除),,09(重复,去除),84(去除),73(去除),03,所以抽取的第个个体的编号是03.
故选:B.
3.C
对于A:由统计图得:年,全国共有幼儿园万所,故A正确;
对于B:由统计图得:年的幼儿园数量比上一年大约增长了,故B正确;
对于C:年我国学前教育毛入园率在持续增加,但毛入园率由适合入读幼儿园的人数及入读幼儿园的人数共同决定,故C不一定正确.
对于D:由统计图得:年我国幼儿园数量及学前教育毛入园率都在持续增加,故D正确;
故选:C.
4.C
设该组数据为,将这组数据中的每一个数都乘以2,则有,平均数为.又,则新数据的方差为,
5.C
解:∵360∶280∶200=9∶7∶5,
∴甲付×65=27
(钱),乙付×65=21
(钱),丙付×65=15
(钱),则C说法错误.
故选:C.
6.A
因为,,
所以,乙组的百分位数为,甲组的百分位数为,
因此,.
故选:A.
7.C
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
因为,而
,
所以中位数位于,设中位数为,
则,
解得:,
故选:C.
8.C
由图知,及格率为,故A错误.
该测试满分同学的百分比为,即有名,B错误.
由图知,中位数为分,平均数为分,故C正确.
由题意,名学生成绩能得优秀的同学有,故D错误.
故选:C
9.C
由表格中的数据可知,,
由频率分布直方图可知,,,
则.
故选:C.
10.AD
对于A选项,万只一次性医用口罩容量很大,应采用抽样调查的方法;
对于B选项,万元存款的现钞的真假检验必须普查,不能放过任何一张假钞;
对于C选项,伞包以伞的质量决定人的生命,必须普查;
对于D选项,防碰撞性能的检测会对产品产生破坏,应采取抽样调查的方法.
故选:AD.
11.ACD
根据雷达图可列表如下:
评分类别
稳固性
创新性
外观造型
做工用料
成本
设计一得分
分
分
分
分
分
设计二得分
分
分
分
分
分
根据表格分析可得A、C、D错误,选项B正确.
故选:ACD.
12.ABC
对于选项A,由图易知各月的平均最低气温都在以上,A正确;
对于选项B,七月的平均最高气温点与平均最低气温点间的距离大于一月的平均最高气温点与平均最低气温点间的距离,所以七月的平均温差比一月的平均温差大,B正确;
对于选项C,三月和十一月的平均最高气温均为,所以C正确;
对于选项D,平均最高气温高于的月份有七月?八月,共2个月份,故D错误.
故选:ABC.
13.
设样本中杉树苗的棵数为,则,解得.
故答案为:40.
14.10.5
由图可知第一组的频率为,
前两组的频率之和为,
则可知其25%分位数在内,设为,
则,解得.
故答案为:10.5.
15.2
由图知,该运动员5场比赛的得分分别为10,13,12,14,16,则平均数为,
∴方差为,所以标准差为2.
16.6
因为“泥塑”社团的人数占总人数的,故“剪纸”社团的人数占总人数的,所以“剪纸”社团的人数为.因为“剪纸”社团中高二年级人数比例为,所以“剪纸”社团中高二年级人数为.由题意知,抽样比为,所以从高二年级“剪纸”社团中抽取的人数为.
故答案为:6
17.
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
18.
(1)由茎叶图可知,乙同学成绩的中位数为.
又由茎叶图可得甲同学成绩的中位数大于或等于,
且甲成绩的中位数小于乙成绩的中位数,所以甲同学成绩的中位数只能为,
故.
(2)甲同学成绩的平均数为,
乙同学成绩的平均数为,
所以甲、乙成绩的平均数相等.
甲同学成绩的方差,
乙同学成绩的方差,
,所以乙同学的成绩更稳定,选乙同学比较合适.
19.(1),;(2)万元.
(1)由题意得,
解得,.
(2)设应该制定的月销售冲刺目标值为万元,则在频率分布直方图中右边的面积为.
最后一组的面积是,
最后两组的面积之和为.
因为,所以位于倒数第二组,
则,解得.
所以该企业的月销售冲刺目标值应该定为万元.
20.
解 (1)根据题意有
解得
所以p=0.4,q=0.25.
补全频率直方图如图所示.
(2)由(1)可知,网购金额低于2千元的频率为0.08+0.12=0.2,
网购金额低于3千元的频率为0.2+0.4=0.6,
所以网购金额的25百分位数在[2,3)内,
则网购金额的25百分位数估计为2+×1=2+0.125≈2.13(千元).
21.
(1)如图示:区间频率最大,所以众数为85,
平均数为:
(2)日销售量[60,90)的频率为,日销量[60,100)的频率为,
故所求的量位于
由得
故每天应该进98千克苹果.
22.
(1)由已知得,故.
.
(2)甲离子残留百分比的平均值的估计值为
.
(3)乙离子残留百分比的中位数的估计值为.
试卷第1页,总3页
一、单选题
1.某中学有300名教师,其中初级教师60名,中级教师150名,高级教师90名.考虑采用分层抽样或系统抽样方法,从全校教师中抽取10人参加一个网络教学座谈会.采用分层抽样时,将初级教师随机编号为1~60,中级教师随机编号为61~210,高级教师随机编号为211~300;采用系统抽样时,将全校教师统一随机编号为1,2,…,300,并将整个编号从小到大依次均分为10组.
给出下列两组样本号码:①7,34,61,88,115,142,169,223,250,288;②26,32,90,100,138,172,188,211,254,297.
则下列结论中错误的是(
)
A.样本①可能为分层抽样
B.样本②可能为分层抽样
C.样本①可能为系统抽样
D.样本②可能为系统抽样
2.总体由编号为的个个体组成,利用随机数表从中抽取个个体,下面提供随机数表的第行到第行:
若从表中第行第列开始向右依次读取,则抽取的第个个体的编号是(
)
A.
B.
C.
D.
3.近年来,我国继续大力发展公办幼儿园,积极扶持普惠性民办幼儿园,使得普惠性学前教育资源迅速增加.如图为国家统计局发布的年幼儿园数量及学前教育毛入园率统计图.根据该统计图,下列说法不一定正确的是(
)
注:
.
A.年,全国共有幼儿园万所
B.年的幼儿园数量比上一年大约增长了
C.年我国适合入读幼儿园的人数在持续增加
D.年我国幼儿园数量及学前教育毛入园率都在持续增加
4.一组数据的方差为,平均数为,将这组数据中的每一个数都乘以2,所得的一组新数据的方差和平均数分别为(
)
A.,
B.,
C.,
D.,
5.分层随机抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱三百六十,乙持钱二百八十,丙持钱二百,凡三人俱出关,关税六十五钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持360钱,乙持280钱,丙持200钱,甲、乙、丙三人一起出关,关税共65钱,要按照各人带多少的比例进行交税,问三人各应付多少税?下列说法错误的是(
)
A.甲应付27钱
B.乙应付21钱
C.丙应付15钱
D.三者中甲付的钱最多,丙付的钱最少
6.已知甲、乙两组数据(已按从小到大的顺序排列):
甲组:、、、、、;
乙组:、、、、、.
若这两组数据的百分位数、百分位数分别相等,则等于(
)
A.
B.
C.
D.
7.2020年12月31日,国务院联防联控机制发布,国药集团中国生物的新冠病毒灭活疫苗已获药监局批准附条件上市,其保护效力达到世界卫生组织及药监局相关标准要求,现已对18至59岁的人提供.根据某地接种年龄样本的频率分布直方图(如图)估计该地接种年龄的中位数为(
)
A.40
B.39
C.38
D.37
8.某高中为了解学生课外知识的积累情况,随机抽取名同学参加课外知识测试,测试共道题,每答对一题得分,答错得分.已知每名同学至少能答对道题,得分不少于分记为及格,不少于分记为优秀,测试成绩百分比分布图如图所示,则下列说法正确的是(
)
A.该次课外知识测试及格率为
B.该次课外知识测试得满分的同学有名
C.该次测试成绩的中位数大于测试成绩的平均数
D.若该校共有名学生,则课外知识测试成绩能得优秀的同学大约有名
9.“脱口秀大赛”上选手的分数分为观众评分和嘉宾评分.组织方将观众评分按照,,分组,绘制频率分布直方图如图所示.嘉宾评分的平均数为,观众评分的平均数为,中位数为,则下列选项正确的是(
)
嘉宾
评分
96
97
96
89
97
98
A.
B.
C.
D.
二、多选题
10.下面的四个问题中,可以用抽样调查方法的是(
)
A.武汉火神山医院供应库房工作人员对新入库的万只一次性医用口罩进行质检
B.中国银行兰山分行对天元公司万元存款的现钞的真假检验
C.空降兵战士检查个伞包及伞的质量
D.一汽大众质检部门检验最新一批斯柯达汽车的防碰撞性能
11.(多选)某装修公司为了解客户对照明系统的需求,对照明系统的两种设计方明系统评分面达图案在稳固性、创新性、外观造型、做工用料以及成本五个方面的满意度评分进行统计,根据统计结果绘制出如图所示的雷达图,则下列说法错误的是(
)
A.客户对两种设计方案在外观造型上没有分歧
B.客户对设计一的满意度的总得分高于设计二的满意度的总得分
C.客户对设计二在创新性方面的满意度高于设计一在创新性方面的满意度
D.客户对两种设计方案在稳固性和做工用料方面的满意度相同
12.某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中点表示十月的平均最高气温约为,点表示四月的平均最低气温约为.下面叙述正确的有(
)
A.各月的平均最低气温都在以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于的月份有5个
三、填空题
13.某林场新种了一批树苗,其中杉树苗棵,树苗棵.为调查树苗的生长情况,按树苗的种类采用分层抽样的方法从中抽取样本.若样本中松树苗有棵,则杉树苗的棵数为________.
14.如图所示是一个样本容量为100的频率分布直方图,则由图形中的数据,可知其25%分位数为____________.
15.已知某篮球运动员在最近5场比赛中的得分的折线图如图所示,则该运动员得分的标准差为__________.
16.某高中针对学生发展要求,开设了富有地方特色的“泥塑”与“剪纸”两个社团,已知报名参加这两个社团的学生共有800人,按照要求每人只能参加一个社团,各年级参加社团的人数情况如下表:
高一年级
高二年级
高三年级
泥塑
a
b
c
剪纸
x
y
z
其中x∶y∶z=5∶3∶2,且“泥塑”社团的人数占两个社团总人数的,为了了解学生对两个社团活动的满意程度,从中抽取一个50人的样本进行调查,则从高二年级“剪纸”社团的学生中应抽取________人.
17.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
四、解答题
18.某地区拟举办汉字听写大赛,某校为了选拔优秀的学生参加比赛,在本校举行了次汉字听写大赛,其中甲、乙两位同学的成绩最优异,由甲、乙两位同学的成绩绘制的茎叶图如图所示.已知甲成绩的中位数小于乙成绩的中位数.
(1)求的值;
(2)若要从甲、乙中选择一名同学参加该地区举办的汉字听写大赛,试从统计学的角度分析,选哪位同学比较合适.
19.年,面对突如其来的新冠肺炎疫情冲击,在党中央领导下,各地区各部门统筹疫情防控和经济社会发展取得显著成效,商业模式创新发展,消费结构升级持续发展.某主打线上零售产品的企业随机抽取了名销售员,统计了其年的月均销售额(单位:万元),将数据按照分成组,制成了如图所示的频率分布直方图.已知组的频数比组多.
(1)求频率分布直方图中和的值;
(2)该企业为了挖掘销售员的工作潜力,对销售员实行冲刺目标管理,即给销售员确定一个具体的冲刺目标,完成这个冲刺目标,则给予额外的奖励,若公司希望恰有的销售人员能够获得额外奖励,求该企业应该制定的月销售冲刺目标值.
20.某网络营销部门随机抽查了某市200名网友在2019年11月11日的网购金额,所得数据如下表:
网购金额(单位:千元)
人数
频率
[0,1)
16
0.08
[1,2)
24
0.12
[2,3)
x
p
[3,4)
y
q
[4,5)
16
0.08
[5,6]
14
0.07
合计
200
1.00
已知网购金额低于3千元与不低于3千元的人数比恰为3∶2.
(1)试确定x,y,p,q的值,并补全频率直方图;
(2)估计网购金额的25百分位数(结果保留3位有效数字).
21.某家水果店的店长为了解本店苹果的日销售情况,记录了近期连续120天苹果的日销售量(单位:),并绘制频率分布直方图如下:
(1)请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数;(同一组中的数据以这组数据所在区间中点的值作代表)
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在10天中,大约有8天可以满足顾客的需求).请问每天应该进多少千克苹果?(精确到整数位)
22.为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成两组,每组100只,其中给A组小鼠服用甲离子溶液,给B组小鼠服用乙离子溶液,给每组小鼠服用的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
记C为事件:“乙离子残留在体内的百分比不低于5.5”,根据直方图得到的估计值为0.70.
(1)求乙离子残留百分比直方图中的值;
(2)估计甲离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
(3)估计乙离子残留百分比的中位数.(保留2位有效数字)
参考答案
1.C
若采用分层抽样,则抽样比例为,
从而初,中,高级教师抽取的人数分别为2,5,3,
所以在编号1~60内抽取2个号码,在编号61~210内抽取5个号码,
在编号211~300内抽取3个号码,样本①,②都符合.
若采用系统抽样,则每30个编号抽取1个号码,
即在编号1~30,31~60,61~90,…,271~300内各抽取1个号码.
因为61,88都在编号61~90范围内,则样本①不符合,
但样本②符合,
2.B
利用随机数表从第行第列开始向右读取,依次为09,84(去除),96(去除),57(去除),,09(重复,去除),84(去除),73(去除),03,所以抽取的第个个体的编号是03.
故选:B.
3.C
对于A:由统计图得:年,全国共有幼儿园万所,故A正确;
对于B:由统计图得:年的幼儿园数量比上一年大约增长了,故B正确;
对于C:年我国学前教育毛入园率在持续增加,但毛入园率由适合入读幼儿园的人数及入读幼儿园的人数共同决定,故C不一定正确.
对于D:由统计图得:年我国幼儿园数量及学前教育毛入园率都在持续增加,故D正确;
故选:C.
4.C
设该组数据为,将这组数据中的每一个数都乘以2,则有,平均数为.又,则新数据的方差为,
5.C
解:∵360∶280∶200=9∶7∶5,
∴甲付×65=27
(钱),乙付×65=21
(钱),丙付×65=15
(钱),则C说法错误.
故选:C.
6.A
因为,,
所以,乙组的百分位数为,甲组的百分位数为,
因此,.
故选:A.
7.C
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
年龄位于的频率为,
因为,而
,
所以中位数位于,设中位数为,
则,
解得:,
故选:C.
8.C
由图知,及格率为,故A错误.
该测试满分同学的百分比为,即有名,B错误.
由图知,中位数为分,平均数为分,故C正确.
由题意,名学生成绩能得优秀的同学有,故D错误.
故选:C
9.C
由表格中的数据可知,,
由频率分布直方图可知,,,
则.
故选:C.
10.AD
对于A选项,万只一次性医用口罩容量很大,应采用抽样调查的方法;
对于B选项,万元存款的现钞的真假检验必须普查,不能放过任何一张假钞;
对于C选项,伞包以伞的质量决定人的生命,必须普查;
对于D选项,防碰撞性能的检测会对产品产生破坏,应采取抽样调查的方法.
故选:AD.
11.ACD
根据雷达图可列表如下:
评分类别
稳固性
创新性
外观造型
做工用料
成本
设计一得分
分
分
分
分
分
设计二得分
分
分
分
分
分
根据表格分析可得A、C、D错误,选项B正确.
故选:ACD.
12.ABC
对于选项A,由图易知各月的平均最低气温都在以上,A正确;
对于选项B,七月的平均最高气温点与平均最低气温点间的距离大于一月的平均最高气温点与平均最低气温点间的距离,所以七月的平均温差比一月的平均温差大,B正确;
对于选项C,三月和十一月的平均最高气温均为,所以C正确;
对于选项D,平均最高气温高于的月份有七月?八月,共2个月份,故D错误.
故选:ABC.
13.
设样本中杉树苗的棵数为,则,解得.
故答案为:40.
14.10.5
由图可知第一组的频率为,
前两组的频率之和为,
则可知其25%分位数在内,设为,
则,解得.
故答案为:10.5.
15.2
由图知,该运动员5场比赛的得分分别为10,13,12,14,16,则平均数为,
∴方差为,所以标准差为2.
16.6
因为“泥塑”社团的人数占总人数的,故“剪纸”社团的人数占总人数的,所以“剪纸”社团的人数为.因为“剪纸”社团中高二年级人数比例为,所以“剪纸”社团中高二年级人数为.由题意知,抽样比为,所以从高二年级“剪纸”社团中抽取的人数为.
故答案为:6
17.
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
18.
(1)由茎叶图可知,乙同学成绩的中位数为.
又由茎叶图可得甲同学成绩的中位数大于或等于,
且甲成绩的中位数小于乙成绩的中位数,所以甲同学成绩的中位数只能为,
故.
(2)甲同学成绩的平均数为,
乙同学成绩的平均数为,
所以甲、乙成绩的平均数相等.
甲同学成绩的方差,
乙同学成绩的方差,
,所以乙同学的成绩更稳定,选乙同学比较合适.
19.(1),;(2)万元.
(1)由题意得,
解得,.
(2)设应该制定的月销售冲刺目标值为万元,则在频率分布直方图中右边的面积为.
最后一组的面积是,
最后两组的面积之和为.
因为,所以位于倒数第二组,
则,解得.
所以该企业的月销售冲刺目标值应该定为万元.
20.
解 (1)根据题意有
解得
所以p=0.4,q=0.25.
补全频率直方图如图所示.
(2)由(1)可知,网购金额低于2千元的频率为0.08+0.12=0.2,
网购金额低于3千元的频率为0.2+0.4=0.6,
所以网购金额的25百分位数在[2,3)内,
则网购金额的25百分位数估计为2+×1=2+0.125≈2.13(千元).
21.
(1)如图示:区间频率最大,所以众数为85,
平均数为:
(2)日销售量[60,90)的频率为,日销量[60,100)的频率为,
故所求的量位于
由得
故每天应该进98千克苹果.
22.
(1)由已知得,故.
.
(2)甲离子残留百分比的平均值的估计值为
.
(3)乙离子残留百分比的中位数的估计值为.
试卷第1页,总3页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
