第十章单元概率单元基础巩固试卷—2020-2021学年高一下学期数学人教A版(2019)必修第二册(含答案)
文档属性
| 名称 | 第十章单元概率单元基础巩固试卷—2020-2021学年高一下学期数学人教A版(2019)必修第二册(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 908.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 10:19:28 | ||
图片预览



文档简介
第十章单元概率单元基础巩固试卷—2020-2021学年高一下学期数学人教版必修第二册
一、单选题
1.下列现象中,是随机现象的有(
)
①在一条公路上,交警记录某一小时通过汽车超过300辆.
②若a为实数,则|a+1|≥0.
③发射一颗炮弹,命中目标.
④检查流水线上一件产品,这件产品是次品.
A.1个
B.2个
C.3个
D.4个
2.如果事件A,B互斥,那么(
)
A.A∪B是必然事件
B.A的对立事件与B的对立事件的和事件是必然事件
C.A的对立事件与B的对立事件是互斥事件
D.A的对立事件与B的对立事件不是互斥事件
3.甲、乙、丙三名同学站成一排,甲站在中间的概率是( )
A.
B.
C.
D.
4.甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即先赢2局者为胜根据以往二人的比赛数据分析,甲在每局比赛中获胜的概率为,则本次比赛中甲获胜的概率为(
)
A.
B.
C.
D.
5.在一个袋子中放个白球,个红球,摇匀后随机摸出个球,与“摸出个白球个红球”互斥而不对立的事件是(
)
A.至少摸出个白球
B.至少摸出个红球
C.摸出个白球
D.摸出个白球或摸出个红球
6.五一放假,甲、乙、丙去厦门旅游的概率分别是、、,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去厦门旅游的概率为(
)
A.
B.
C.
D.
7.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为(
)
A.
B.
C.
D.
8.对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A=“两次都击中飞机”,B=“两次都没击中飞机”,C=“恰有一枚炮弹击中飞机”,D=“至少有一枚炮弹击中飞机”,下列关系不正确的是(
)
A.A?D
B.B∩D=
C.A∪C=D
D.A∪B=B∪D
二、多选题
9.下列各对事件中,为相互独立事件的是(
)
A.掷一枚骰子一次,事件M“出现偶数点”;事件N“出现3点或6点”
B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到白球”
C.袋中有3白?2黑共5个大小相同的小球,依次不放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到黑球”
D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲?乙两组中各选1名同学参加演讲比赛,事件M“从甲组中选出1名男生”,事件N“从乙组中选出1名女生”
10.某展会安排了分别标有序号为“号”“号”“号”的三辆车,等可能的随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计了两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“号”车的概率分别为,则(
)
A.
B.
C.
D.
11.同时抛掷两枚质地均匀的骰子,则下列说法正确的是(
)
A.一共有种不同的结果
B.两枚骰子向上的点数相同的概率是
C.两枚骰子向上的点数之和为的概率是
D.两枚骰子向上的点数之差的绝对值小于的概率为
12.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种做法(
)
A.每个班被选到的概率都为
B.4班和10班被选到的概率都为
C.2班和12班被选到的概率最小
D.7班被选到的概率最大
三、填空题
13.一叠卡片共有10张,分别写上1~10十个数字,将它们背面朝上洗匀后,任意抽出一张卡片,则P(抽到卡片上的数字大于6)=________,P(抽到卡片上的数字大于7小于9)=________,P(抽到卡片上的数字为偶数)=________.
14.已知随机事件A,B互为对立事件,且,则___________.
15.从含有两件正品和一件次品b的3件产品中,按先后顺序任意取出两件产品,每次取出后不放回,取出的两件产品都是正品的概率为__________.
16.从,,,,这五个数中,随机抽取一个数,作为正比例函数和二次函数中的的值,恰好使所得的正比例函数的图象经过第二、四象限,且二次函数的图象的开口向上的概率为________.
17.辛普森悖论(Simpson’sParadox)有人译为辛普森诡论,在统计学中亦有人称为“逆论”,甚至有人视之为“魔术”.辛普森悖论为英国统计学家E.H.辛普森(E.H.Simpson)于1951年提出的,辛普森悖论的内容大意是“在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论:关于某高校法学院和商学院新学期已完成的招生情况,现有如下数据:
某高校
申请人数
性别
录取率
法学院
200人
男
50%
女
70%
商学院
300人
男
60%
女
90%
对于此次招生,给出下列四个结论:
①法学院的录取率小于商学院的录取率;
②这两个学院所有男生的录取率小于这两个学院所有女生的录取率;
③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率;
④法学院的录取率不一定小于这两个学院所有学生的录取率.
其中,所有正确结论的序号是___________.
四、解答题
18.袋中装有红球、黑球、黄球、绿球共12个.从中任取一球,取到红球的概率是,取到黑球或黄球的概率是,取到黄球或绿球的概率是.试求取到黑球、黄球、绿球的概率各是多少.
19.已知在某次1500米体能测试中,甲、乙、丙3人各自通过测试的概率分别为,,.求:
(1)3人都通过体能测试的概率;
(2)只有2人通过体能测试的概率;
(3)只有1人通过体能测试的概率.
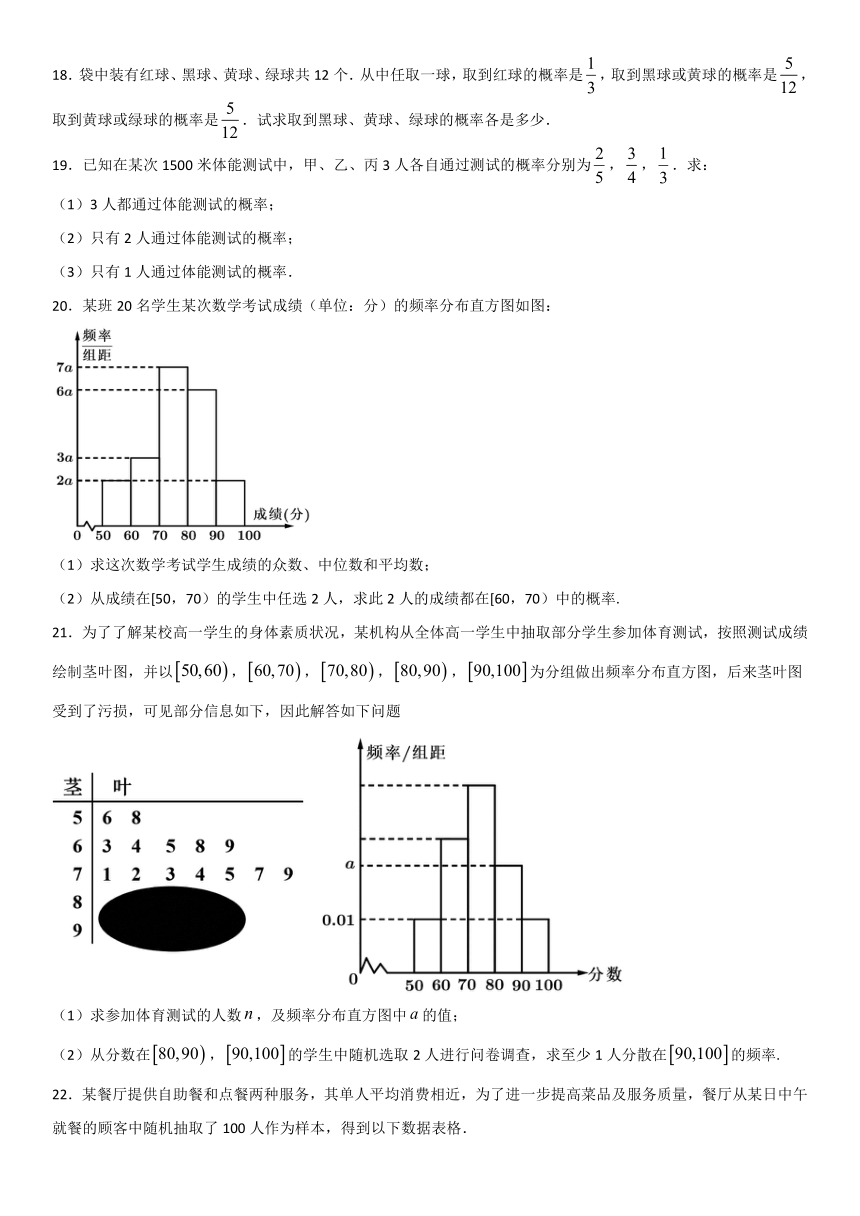
20.某班20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
(1)求这次数学考试学生成绩的众数、中位数和平均数;
(2)从成绩在[50,70)的学生中任选2人,求此2人的成绩都在[60,70)中的概率.
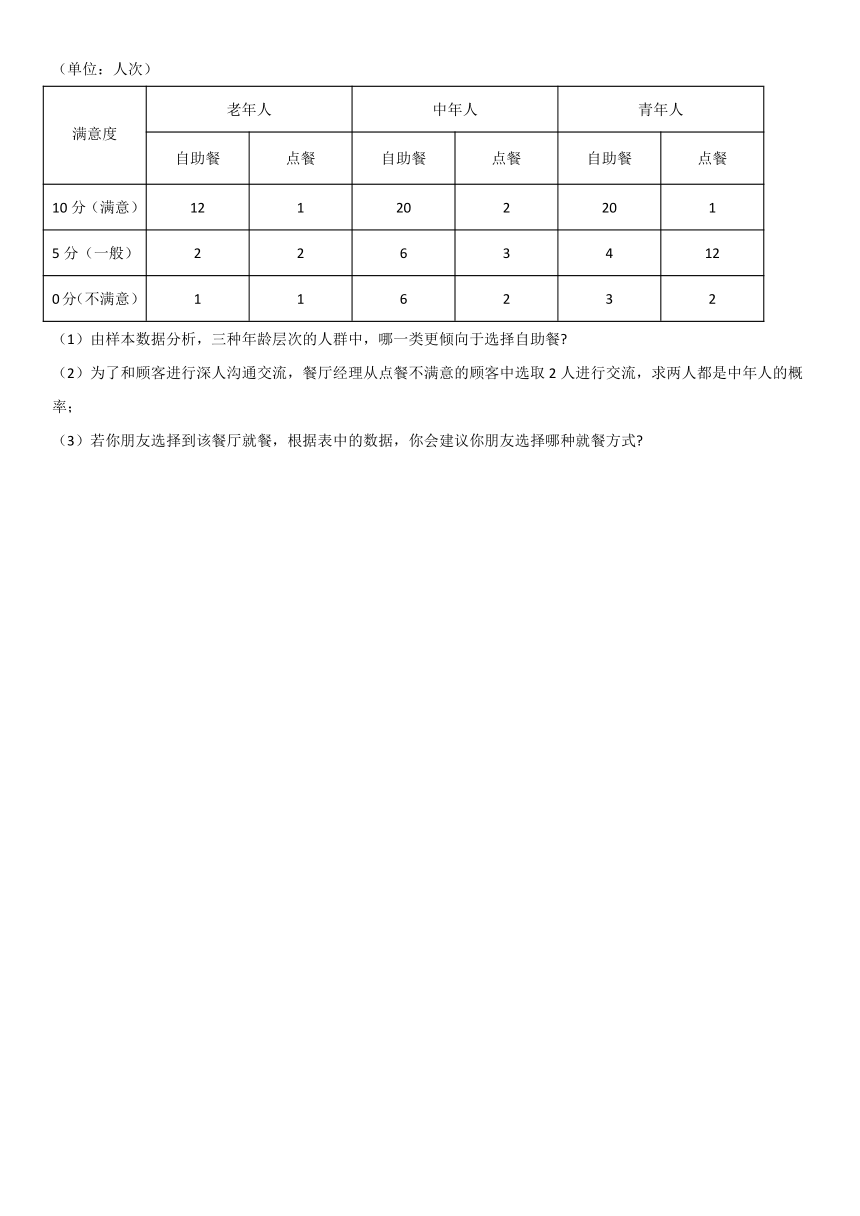
21.为了了解某校高一学生的身体素质状况,某机构从全体高一学生中抽取部分学生参加体育测试,按照测试成绩绘制茎叶图,并以,,,,为分组做出频率分布直方图,后来茎叶图受到了污损,可见部分信息如下,因此解答如下问题
(1)求参加体育测试的人数,及频率分布直方图中的值;
(2)从分数在,的学生中随机选取2人进行问卷调查,求至少1人分散在的频率.
22.某餐厅提供自助餐和点餐两种服务,其单人平均消费相近,为了进一步提高菜品及服务质量,餐厅从某日中午就餐的顾客中随机抽取了100人作为样本,得到以下数据表格.
(单位:人次)
满意度
老年人
中年人
青年人
自助餐
点餐
自助餐
点餐
自助餐
点餐
10分(满意)
12
1
20
2
20
1
5分(一般)
2
2
6
3
4
12
0分(不满意)
1
1
6
2
3
2
(1)由样本数据分析,三种年龄层次的人群中,哪一类更倾向于选择自助餐?
(2)为了和顾客进行深人沟通交流,餐厅经理从点餐不满意的顾客中选取2人进行交流,求两人都是中年人的概率;
(3)若你朋友选择到该餐厅就餐,根据表中的数据,你会建议你朋友选择哪种就餐方式?
参考答案
1.C
当a为实数时,|a+1|≥0恒成立,是必然现象,其余3个均为随机现象.
所以是随机现象的有3个.
故选:C
2.B
A.
因为事件A,B互斥,若对立,则A∪B是必然事件,若不对立,则A∪B不是必然事件,故错误;
B.
A的对立事件与B的对立事件的和事件是必然事件,故正确;
C.
若事件A,B互斥,不对立,则
A的对立事件与B的对立事件不是互斥事件,故错误;
D.
若事件A,B互斥,且对立,则A的对立事件与B的对立事件是对立事件,故错误;
故选:B
3. C
解析 样本点有:甲乙丙、甲丙乙、乙甲丙、乙丙甲、丙甲乙、丙乙甲共六个.甲站在中间的事件包括:乙甲丙、丙甲乙,共2个,所以甲站在中间的概率P==.
4.D
甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即先赢2局者为胜,甲在每局比赛中获胜的概率为,
则甲获胜有以下三种情况:
第一局胜、第二局胜,则甲获胜概率为;
第一局胜、第二局负、第三局胜,则甲获胜概率为;
第一局负、第二局胜、第三局胜,则甲获胜概率为;
综上可知甲获胜概率为,
故选:D.
5.C
对于A,至少摸出个白球与摸出个白球个红球不是互斥事件;
对于B,至少摸出个红球与摸出个白球个红球不是互斥事件;
对于C,摸出个白球与摸出个白球个红球是互斥而不对立事件;
对于D,摸出个白球或摸出个红球与摸出个白球个红球是互斥也是对立事件.
故选:C.
6.B
记事件至少有1人去厦门旅游,其对立事件为:三人都不去厦门旅游,
由独立事件的概率公式可得,
由对立事件的概率公式可得,
故选:B.
7.A
从5张卡片中随机抽取1张,放回后再随机抽取1张的情况如图:
基本事件总数为25,
第一张卡片上的数大于第二张卡片上的数的事件数为10,
故所求概率.
故选:A.
8.D
“恰有一枚炮弹击中飞机”指第一枚击中第二枚没中或第一枚没中第二枚击中,“至少有一枚炮弹击中”包含两种情况:恰有一枚炮弹击中,两枚炮弹都击中.故A?D
,A∪C=D
B,D为互斥事件,B∩D=;
A∪B=“两个飞机都击中或者都没击中”,B∪D为必然事件,这两者不相等
故选:D
9.ABD
在A中,样本空间,事件,事件,事件,
∴,,,
即,故事件M与N相互独立,A正确.
在B中,根据事件的特点易知,事件M是否发生对事件发生的概率没有影响,故M与N是相互独立事件,B正确;
在C中,由于第1次摸到球不放回,因此会对第2次摸到球的概率产生影响,因此不是相互独立事件,C错误;
在D中,从甲组中选出1名男生与从乙组中选出1名女生这两个事件的发生没有影响,所以它们是相互独立事件,D正确.
故选:ABD.
10.ACD
由题意,分别标有序号为“1号”“2号”“3号”的三辆车,等坑随机顺序前往酒店接嘉宾,
基本事件有:,共6种,
设计两种方案:方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车,
则方案一坐到“3号”车包含的基本事件有:,共有3种,
所以方案一的概率为;
方案二:直接乘坐第一辆车,则方案二坐到“号”车的概率为,
所以.
故选:ACD
.
11.ABD
同时抛掷两枚质地均匀的骰子,一共有种不同的结果,A选项正确;
对于B选项,事件“两枚骰子向上的点数相同”所包含的基本事件有:、、、、、,共种不同的结果,所求概率为,B选项正确;
对于C选项,事件“两枚骰子向上的点数之和为”所包含的基本事件有:、、、,共种不同的结果,所求概率为,C选项错误;
对于D选项,事件“两枚骰子向上的点数之差的绝对值不小于”所包含的基本事件有:、、、、、,共种不同的结果,
因此,事件“两枚骰子向上的点数之差的绝对值小于”的概率为,D选项正确.
故选:ABD.
12.BCD
解:题意将两枚骰子的点数之和列出下表:
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
由表得,7班被选到的概率最大为,
6班与8班被选到的概率都为,
5班与9班被选到的概率都为,
4班与10班被选到的概率都为,
3班与11班被选到的概率都为,
2班与12班被选到的概率都为.
故选:BCD.
13.
解析:从10张卡片中任抽一张有10种抽法,即10个基本事件,
其中抽到卡片上的数字大于6包括4个基本事件.
由于抽到每一张卡片的可能性都相等,
故P(抽到卡片上的数字大于6);
抽到卡片上的数字大于7小于9包括1个基本事件,
可得P(抽到卡片上的数字大于7小于9);
抽到卡片上的数字为偶数包括5个基本事件,
P(抽到卡片上的数字为偶数).
故答案为:;;.
14.
因为随机事件A,B互为对立事件,故,而故,
故,
故答案为:.
15.
从含有两件正品和一件次品的3件产品中,
按先后顺序任意取出两件产品,每次取出后不放回,
共包含,,,,,6个基本事件,
取出的两件产品都是正品包含,2个基本事件,
∴取出的两件产品都是正品的概率为,
故答案为:.
16.
由,解得
则这五个数中满足条件的有,
即使所得的正比例函数的图象经过第二、四象限,且二次函数的图象的开口向上的概率为
故答案为:
17.②④
设申请法学院的男生人数为,女生人数为,则,
法学院的录取率为,
设申请商学院的男生人数为,女生人数为,则,
商学院的录取率为,
由,
该值的正负不确定,所以①错误,④正确;
这两个学院所有男生的录取率为,
这两个学院所有女生的录取率为,
因为,
所以②正确;③错误.
故答案为:②④.
18.取到黑球的概率是,取到黄球的概率是,取到绿球的概率是.
解:从袋中任取一球,记事件“取到红球”“取到黑球”“取到黄球”和“取到绿球”分别为A,B,C,D,则事件A,B,C,D显然是两两互斥的.
由题意,得
即
解得
故取到黑球的概率是,取到黄球的概率是,取到绿球的概率是.
19.(1);(2);(3).
解:设事件A=“甲通过体能测试”,事件B=“乙通过体能测试”,事件C=“丙通过体能测试”,由题意有:P(A)=,P(B)=,P(C)=.
(1)设事件M1=“甲、乙、丙3人都通过体能测试”,
即事件M1=ABC,由事件A,B,C相互独立可得
P(M1)=P(ABC)=P(A)·P(B)·P(C)=××=.
(2)设事件M2=“甲、乙、丙3人中只有2人通过体能测试”,
则M2=AB+AC+BC,
由于事件A,B,C,,,均相互独立,
并且事件AB,AC,BC两两互斥,
因此P(M2)=P(A)·P(B)·P()+P(A)·P()·P(C)+P()·P(B)·P(C)
=××+××+××=.
(3)设事件M3=“甲、乙、丙3人中只有1人通过体能测试”,
则M3=A+B+C,
由于事件A,B,C,,,均相互独立,
并且事件A,B,C两两互斥,
因此P(M3)=P(A)·P()·P()+P()·P(B)·P()+P()·P()·P(C)
=××+××+××=.
20.(1)众数是75分,中位数为分,平均数为分;(2).
(1)根据直方图知组距为10,
由,解得.
数学成绩的众数是75分.
由,得平均数为分.
设中位数为x分,则由,
得.
所以众数是75分,中位数为分,平均数为分;
(2)成绩落在[50,60)中的学生人数为,
成绩落在[60,70)中的学生人数为;
记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,
则从成绩在[50,70)的学生中任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的事件有CD,CE,DE共3个,
故所求概率为.
21.(1),;(2).
(1)由题意可得:
测试成绩位于的频数为,频率为,
所以,
测试成绩位于的频率等于测试成绩位于的频率为,
所以测试成绩位于的有人,
测试成绩位于,,的有人,
所以测试成绩位于有人,
所以,
(2)由(1)知分数在的有人分别记为,分数在的有人记为,
从中随机取人基本事件有:共个,
至少1人分散在的基本事件有共个,
所以至少1人分散在的频率为.
22.(1)中年人更倾向于选择自助餐;(2);(3)建议其选择自助餐.
(1)由题知,老年人选择自助餐的频率,
中年人选择自助餐的频率,
青年人选择自助餐的频率,
则,
即中年人更倾向于选择自助餐.
(2)点餐不满意的人群中,老年人1人(设为),中年人2人(设为,),青年人2人(设为,).
从中选取2人,其基本事件有,,,,,
,,,,,共10个
基本事件,其中2人都是中年人仅有一个符合题意;
故两人都是中年人的概率为.
(3)由表可知,自助餐满意的均值为:.
点餐满意的均值为:
,故建议其选择自助餐.
试卷第1页,总3页
一、单选题
1.下列现象中,是随机现象的有(
)
①在一条公路上,交警记录某一小时通过汽车超过300辆.
②若a为实数,则|a+1|≥0.
③发射一颗炮弹,命中目标.
④检查流水线上一件产品,这件产品是次品.
A.1个
B.2个
C.3个
D.4个
2.如果事件A,B互斥,那么(
)
A.A∪B是必然事件
B.A的对立事件与B的对立事件的和事件是必然事件
C.A的对立事件与B的对立事件是互斥事件
D.A的对立事件与B的对立事件不是互斥事件
3.甲、乙、丙三名同学站成一排,甲站在中间的概率是( )
A.
B.
C.
D.
4.甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即先赢2局者为胜根据以往二人的比赛数据分析,甲在每局比赛中获胜的概率为,则本次比赛中甲获胜的概率为(
)
A.
B.
C.
D.
5.在一个袋子中放个白球,个红球,摇匀后随机摸出个球,与“摸出个白球个红球”互斥而不对立的事件是(
)
A.至少摸出个白球
B.至少摸出个红球
C.摸出个白球
D.摸出个白球或摸出个红球
6.五一放假,甲、乙、丙去厦门旅游的概率分别是、、,假定三人的行动相互之间没有影响,那么这段时间内至少有1人去厦门旅游的概率为(
)
A.
B.
C.
D.
7.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为(
)
A.
B.
C.
D.
8.对空中飞行的飞机连续射击两次,每次发射一枚炮弹,设A=“两次都击中飞机”,B=“两次都没击中飞机”,C=“恰有一枚炮弹击中飞机”,D=“至少有一枚炮弹击中飞机”,下列关系不正确的是(
)
A.A?D
B.B∩D=
C.A∪C=D
D.A∪B=B∪D
二、多选题
9.下列各对事件中,为相互独立事件的是(
)
A.掷一枚骰子一次,事件M“出现偶数点”;事件N“出现3点或6点”
B.袋中有3白、2黑共5个大小相同的小球,依次有放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到白球”
C.袋中有3白?2黑共5个大小相同的小球,依次不放回地摸两球,事件M“第一次摸到白球”,事件N“第二次摸到黑球”
D.甲组3名男生,2名女生;乙组2名男生,3名女生,现从甲?乙两组中各选1名同学参加演讲比赛,事件M“从甲组中选出1名男生”,事件N“从乙组中选出1名女生”
10.某展会安排了分别标有序号为“号”“号”“号”的三辆车,等可能的随机顺序前往酒店接嘉宾.某嘉宾突发奇想,设计了两种乘车方案.方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车;方案二:直接乘坐第一辆车.记方案一与方案二坐到“号”车的概率分别为,则(
)
A.
B.
C.
D.
11.同时抛掷两枚质地均匀的骰子,则下列说法正确的是(
)
A.一共有种不同的结果
B.两枚骰子向上的点数相同的概率是
C.两枚骰子向上的点数之和为的概率是
D.两枚骰子向上的点数之差的绝对值小于的概率为
12.某年级有12个班,现要从2班到12班中选1个班的学生参加一项活动,有人提议:掷两个骰子,得到的点数之和是几就选几班,这种做法(
)
A.每个班被选到的概率都为
B.4班和10班被选到的概率都为
C.2班和12班被选到的概率最小
D.7班被选到的概率最大
三、填空题
13.一叠卡片共有10张,分别写上1~10十个数字,将它们背面朝上洗匀后,任意抽出一张卡片,则P(抽到卡片上的数字大于6)=________,P(抽到卡片上的数字大于7小于9)=________,P(抽到卡片上的数字为偶数)=________.
14.已知随机事件A,B互为对立事件,且,则___________.
15.从含有两件正品和一件次品b的3件产品中,按先后顺序任意取出两件产品,每次取出后不放回,取出的两件产品都是正品的概率为__________.
16.从,,,,这五个数中,随机抽取一个数,作为正比例函数和二次函数中的的值,恰好使所得的正比例函数的图象经过第二、四象限,且二次函数的图象的开口向上的概率为________.
17.辛普森悖论(Simpson’sParadox)有人译为辛普森诡论,在统计学中亦有人称为“逆论”,甚至有人视之为“魔术”.辛普森悖论为英国统计学家E.H.辛普森(E.H.Simpson)于1951年提出的,辛普森悖论的内容大意是“在某个条件下的两组数据,分别讨论时都会满足某种性质,可是一旦合并考虑,却可能导致相反的结论.”下面这个案例可以让我们感受到这个悖论:关于某高校法学院和商学院新学期已完成的招生情况,现有如下数据:
某高校
申请人数
性别
录取率
法学院
200人
男
50%
女
70%
商学院
300人
男
60%
女
90%
对于此次招生,给出下列四个结论:
①法学院的录取率小于商学院的录取率;
②这两个学院所有男生的录取率小于这两个学院所有女生的录取率;
③这两个学院所有男生的录取率不一定小于这两个学院所有女生的录取率;
④法学院的录取率不一定小于这两个学院所有学生的录取率.
其中,所有正确结论的序号是___________.
四、解答题
18.袋中装有红球、黑球、黄球、绿球共12个.从中任取一球,取到红球的概率是,取到黑球或黄球的概率是,取到黄球或绿球的概率是.试求取到黑球、黄球、绿球的概率各是多少.
19.已知在某次1500米体能测试中,甲、乙、丙3人各自通过测试的概率分别为,,.求:
(1)3人都通过体能测试的概率;
(2)只有2人通过体能测试的概率;
(3)只有1人通过体能测试的概率.
20.某班20名学生某次数学考试成绩(单位:分)的频率分布直方图如图:
(1)求这次数学考试学生成绩的众数、中位数和平均数;
(2)从成绩在[50,70)的学生中任选2人,求此2人的成绩都在[60,70)中的概率.
21.为了了解某校高一学生的身体素质状况,某机构从全体高一学生中抽取部分学生参加体育测试,按照测试成绩绘制茎叶图,并以,,,,为分组做出频率分布直方图,后来茎叶图受到了污损,可见部分信息如下,因此解答如下问题
(1)求参加体育测试的人数,及频率分布直方图中的值;
(2)从分数在,的学生中随机选取2人进行问卷调查,求至少1人分散在的频率.
22.某餐厅提供自助餐和点餐两种服务,其单人平均消费相近,为了进一步提高菜品及服务质量,餐厅从某日中午就餐的顾客中随机抽取了100人作为样本,得到以下数据表格.
(单位:人次)
满意度
老年人
中年人
青年人
自助餐
点餐
自助餐
点餐
自助餐
点餐
10分(满意)
12
1
20
2
20
1
5分(一般)
2
2
6
3
4
12
0分(不满意)
1
1
6
2
3
2
(1)由样本数据分析,三种年龄层次的人群中,哪一类更倾向于选择自助餐?
(2)为了和顾客进行深人沟通交流,餐厅经理从点餐不满意的顾客中选取2人进行交流,求两人都是中年人的概率;
(3)若你朋友选择到该餐厅就餐,根据表中的数据,你会建议你朋友选择哪种就餐方式?
参考答案
1.C
当a为实数时,|a+1|≥0恒成立,是必然现象,其余3个均为随机现象.
所以是随机现象的有3个.
故选:C
2.B
A.
因为事件A,B互斥,若对立,则A∪B是必然事件,若不对立,则A∪B不是必然事件,故错误;
B.
A的对立事件与B的对立事件的和事件是必然事件,故正确;
C.
若事件A,B互斥,不对立,则
A的对立事件与B的对立事件不是互斥事件,故错误;
D.
若事件A,B互斥,且对立,则A的对立事件与B的对立事件是对立事件,故错误;
故选:B
3. C
解析 样本点有:甲乙丙、甲丙乙、乙甲丙、乙丙甲、丙甲乙、丙乙甲共六个.甲站在中间的事件包括:乙甲丙、丙甲乙,共2个,所以甲站在中间的概率P==.
4.D
甲、乙两人进行乒乓球比赛,比赛规则为“3局2胜”,即先赢2局者为胜,甲在每局比赛中获胜的概率为,
则甲获胜有以下三种情况:
第一局胜、第二局胜,则甲获胜概率为;
第一局胜、第二局负、第三局胜,则甲获胜概率为;
第一局负、第二局胜、第三局胜,则甲获胜概率为;
综上可知甲获胜概率为,
故选:D.
5.C
对于A,至少摸出个白球与摸出个白球个红球不是互斥事件;
对于B,至少摸出个红球与摸出个白球个红球不是互斥事件;
对于C,摸出个白球与摸出个白球个红球是互斥而不对立事件;
对于D,摸出个白球或摸出个红球与摸出个白球个红球是互斥也是对立事件.
故选:C.
6.B
记事件至少有1人去厦门旅游,其对立事件为:三人都不去厦门旅游,
由独立事件的概率公式可得,
由对立事件的概率公式可得,
故选:B.
7.A
从5张卡片中随机抽取1张,放回后再随机抽取1张的情况如图:
基本事件总数为25,
第一张卡片上的数大于第二张卡片上的数的事件数为10,
故所求概率.
故选:A.
8.D
“恰有一枚炮弹击中飞机”指第一枚击中第二枚没中或第一枚没中第二枚击中,“至少有一枚炮弹击中”包含两种情况:恰有一枚炮弹击中,两枚炮弹都击中.故A?D
,A∪C=D
B,D为互斥事件,B∩D=;
A∪B=“两个飞机都击中或者都没击中”,B∪D为必然事件,这两者不相等
故选:D
9.ABD
在A中,样本空间,事件,事件,事件,
∴,,,
即,故事件M与N相互独立,A正确.
在B中,根据事件的特点易知,事件M是否发生对事件发生的概率没有影响,故M与N是相互独立事件,B正确;
在C中,由于第1次摸到球不放回,因此会对第2次摸到球的概率产生影响,因此不是相互独立事件,C错误;
在D中,从甲组中选出1名男生与从乙组中选出1名女生这两个事件的发生没有影响,所以它们是相互独立事件,D正确.
故选:ABD.
10.ACD
由题意,分别标有序号为“1号”“2号”“3号”的三辆车,等坑随机顺序前往酒店接嘉宾,
基本事件有:,共6种,
设计两种方案:方案一:不乘坐第一辆车,若第二辆车的车序号大于第一辆车的车序号,就乘坐此车,否则乘坐第三辆车,
则方案一坐到“3号”车包含的基本事件有:,共有3种,
所以方案一的概率为;
方案二:直接乘坐第一辆车,则方案二坐到“号”车的概率为,
所以.
故选:ACD
.
11.ABD
同时抛掷两枚质地均匀的骰子,一共有种不同的结果,A选项正确;
对于B选项,事件“两枚骰子向上的点数相同”所包含的基本事件有:、、、、、,共种不同的结果,所求概率为,B选项正确;
对于C选项,事件“两枚骰子向上的点数之和为”所包含的基本事件有:、、、,共种不同的结果,所求概率为,C选项错误;
对于D选项,事件“两枚骰子向上的点数之差的绝对值不小于”所包含的基本事件有:、、、、、,共种不同的结果,
因此,事件“两枚骰子向上的点数之差的绝对值小于”的概率为,D选项正确.
故选:ABD.
12.BCD
解:题意将两枚骰子的点数之和列出下表:
1
2
3
4
5
6
1
2
3
4
5
6
7
2
3
4
5
6
7
8
3
4
5
6
7
8
9
4
5
6
7
8
9
10
5
6
7
8
9
10
11
6
7
8
9
10
11
12
由表得,7班被选到的概率最大为,
6班与8班被选到的概率都为,
5班与9班被选到的概率都为,
4班与10班被选到的概率都为,
3班与11班被选到的概率都为,
2班与12班被选到的概率都为.
故选:BCD.
13.
解析:从10张卡片中任抽一张有10种抽法,即10个基本事件,
其中抽到卡片上的数字大于6包括4个基本事件.
由于抽到每一张卡片的可能性都相等,
故P(抽到卡片上的数字大于6);
抽到卡片上的数字大于7小于9包括1个基本事件,
可得P(抽到卡片上的数字大于7小于9);
抽到卡片上的数字为偶数包括5个基本事件,
P(抽到卡片上的数字为偶数).
故答案为:;;.
14.
因为随机事件A,B互为对立事件,故,而故,
故,
故答案为:.
15.
从含有两件正品和一件次品的3件产品中,
按先后顺序任意取出两件产品,每次取出后不放回,
共包含,,,,,6个基本事件,
取出的两件产品都是正品包含,2个基本事件,
∴取出的两件产品都是正品的概率为,
故答案为:.
16.
由,解得
则这五个数中满足条件的有,
即使所得的正比例函数的图象经过第二、四象限,且二次函数的图象的开口向上的概率为
故答案为:
17.②④
设申请法学院的男生人数为,女生人数为,则,
法学院的录取率为,
设申请商学院的男生人数为,女生人数为,则,
商学院的录取率为,
由,
该值的正负不确定,所以①错误,④正确;
这两个学院所有男生的录取率为,
这两个学院所有女生的录取率为,
因为,
所以②正确;③错误.
故答案为:②④.
18.取到黑球的概率是,取到黄球的概率是,取到绿球的概率是.
解:从袋中任取一球,记事件“取到红球”“取到黑球”“取到黄球”和“取到绿球”分别为A,B,C,D,则事件A,B,C,D显然是两两互斥的.
由题意,得
即
解得
故取到黑球的概率是,取到黄球的概率是,取到绿球的概率是.
19.(1);(2);(3).
解:设事件A=“甲通过体能测试”,事件B=“乙通过体能测试”,事件C=“丙通过体能测试”,由题意有:P(A)=,P(B)=,P(C)=.
(1)设事件M1=“甲、乙、丙3人都通过体能测试”,
即事件M1=ABC,由事件A,B,C相互独立可得
P(M1)=P(ABC)=P(A)·P(B)·P(C)=××=.
(2)设事件M2=“甲、乙、丙3人中只有2人通过体能测试”,
则M2=AB+AC+BC,
由于事件A,B,C,,,均相互独立,
并且事件AB,AC,BC两两互斥,
因此P(M2)=P(A)·P(B)·P()+P(A)·P()·P(C)+P()·P(B)·P(C)
=××+××+××=.
(3)设事件M3=“甲、乙、丙3人中只有1人通过体能测试”,
则M3=A+B+C,
由于事件A,B,C,,,均相互独立,
并且事件A,B,C两两互斥,
因此P(M3)=P(A)·P()·P()+P()·P(B)·P()+P()·P()·P(C)
=××+××+××=.
20.(1)众数是75分,中位数为分,平均数为分;(2).
(1)根据直方图知组距为10,
由,解得.
数学成绩的众数是75分.
由,得平均数为分.
设中位数为x分,则由,
得.
所以众数是75分,中位数为分,平均数为分;
(2)成绩落在[50,60)中的学生人数为,
成绩落在[60,70)中的学生人数为;
记成绩落在[50,60)中的2人为A,B,成绩落在[60,70)中的3人为C,D,E,
则从成绩在[50,70)的学生中任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在[60,70)中的事件有CD,CE,DE共3个,
故所求概率为.
21.(1),;(2).
(1)由题意可得:
测试成绩位于的频数为,频率为,
所以,
测试成绩位于的频率等于测试成绩位于的频率为,
所以测试成绩位于的有人,
测试成绩位于,,的有人,
所以测试成绩位于有人,
所以,
(2)由(1)知分数在的有人分别记为,分数在的有人记为,
从中随机取人基本事件有:共个,
至少1人分散在的基本事件有共个,
所以至少1人分散在的频率为.
22.(1)中年人更倾向于选择自助餐;(2);(3)建议其选择自助餐.
(1)由题知,老年人选择自助餐的频率,
中年人选择自助餐的频率,
青年人选择自助餐的频率,
则,
即中年人更倾向于选择自助餐.
(2)点餐不满意的人群中,老年人1人(设为),中年人2人(设为,),青年人2人(设为,).
从中选取2人,其基本事件有,,,,,
,,,,,共10个
基本事件,其中2人都是中年人仅有一个符合题意;
故两人都是中年人的概率为.
(3)由表可知,自助餐满意的均值为:.
点餐满意的均值为:
,故建议其选择自助餐.
试卷第1页,总3页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
