统计单元同步过关卷-2020-2021学年高一下学期数学人教A版(2019)必修第二册(含解析)
文档属性
| 名称 | 统计单元同步过关卷-2020-2021学年高一下学期数学人教A版(2019)必修第二册(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-14 00:00:00 | ||
图片预览



文档简介
高一数学第二学期第统计单元同步过关卷-2020-2021学年人教A版(2019)必修第二册
一、单选题
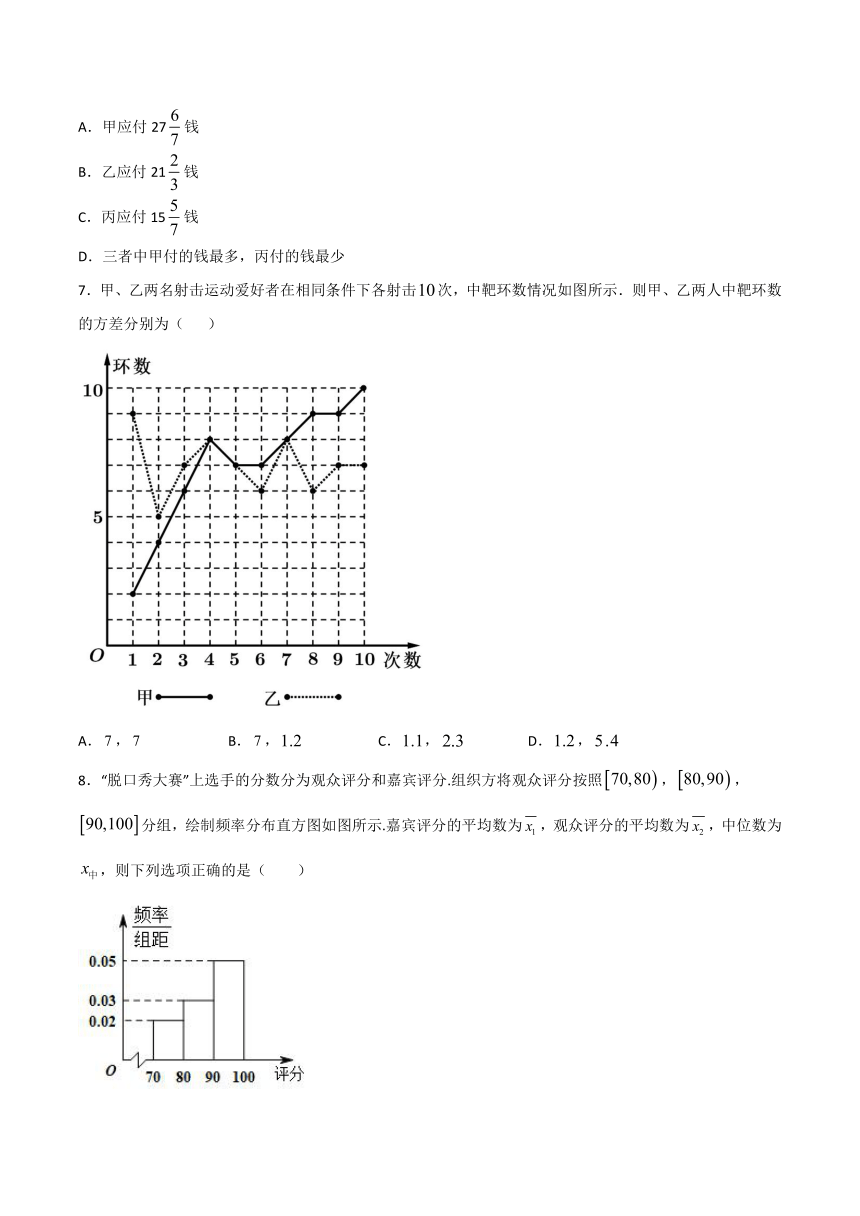
1.某市通过统计50个大型社区产生的日均垃圾量,绘制了如下图所示的频率分布直方图,数据的分组依次为:,,,,,,.为了鼓励率先实施垃圾分类回收,将日均垃圾量不少于14吨的社区划定为试点社区,则这样的试点社区个数是(
).
A.4
B.10
C.19
D.40
2.如图为某商场一天营业额的扇形统计图,根据统计图你不能得出的信息为(
)
A.该商场家用电器销售额为全商场营业额的40%
B.服装鞋帽和百货日杂共售出29000元
C.副食的销售额为该商场营业额的10%
D.家用电器部所得利润最高
3.如图为2011—2019年中国白酒行业各类型专利申请情况.
根据图中数据,下列说法不正确的是(
)
A.2011-2016年中国发明专利量逐年增长
B.2019年中国发明专利量为1458件,约比2018年减少了44.22%
C.2016年之后,白酒行业专利申请总量出现下滑,且实用新型专利量、发明专利量、外观专利量也在逐年下滑
D.2011年中国实用新型专利量在三类专利申请总量中约占7.69%
4.总体由编号为的个个体组成,利用随机数表从中抽取个个体,下面提供随机数表的第行到第行:
若从表中第行第列开始向右依次读取,则抽取的第个个体的编号是(
)
A.
B.
C.
D.
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为x,y,105,109,110.已知她的五次数学成绩数据的平均数为108分,方差为35.2,则|x-y|的值为(
)
A.15
B.16
C.17
D.18
6.分层随机抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱三百六十,乙持钱二百八十,丙持钱二百,凡三人俱出关,关税六十五钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持360钱,乙持280钱,丙持200钱,甲、乙、丙三人一起出关,关税共65钱,要按照各人带多少的比例进行交税,问三人各应付多少税?下列说法错误的是(
)
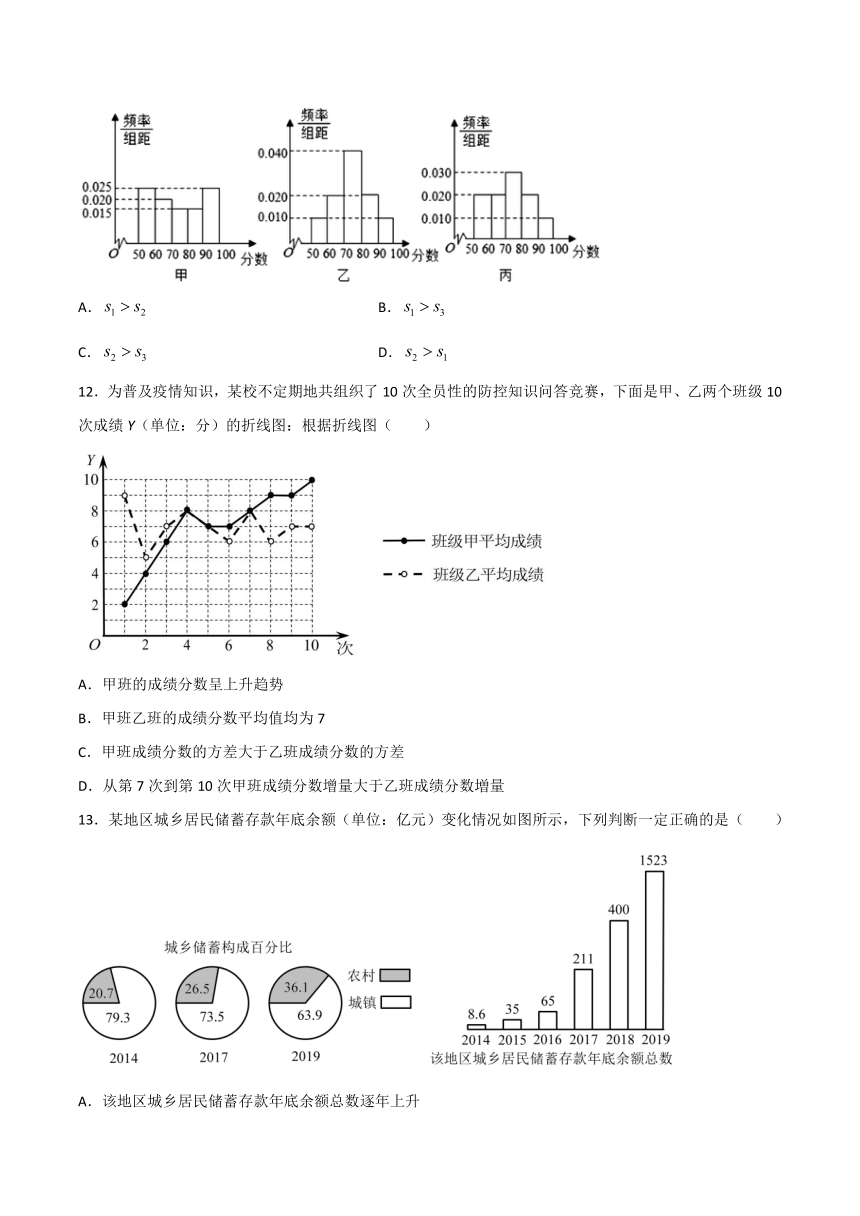
A.甲应付27钱
B.乙应付21钱
C.丙应付15钱
D.三者中甲付的钱最多,丙付的钱最少
7.甲、乙两名射击运动爱好者在相同条件下各射击次,中靶环数情况如图所示.则甲、乙两人中靶环数的方差分别为(
)
A.,
B.,
C.,
D.,
8.“脱口秀大赛”上选手的分数分为观众评分和嘉宾评分.组织方将观众评分按照,,分组,绘制频率分布直方图如图所示.嘉宾评分的平均数为,观众评分的平均数为,中位数为,则下列选项正确的是(
)
嘉宾
评分
96
97
96
89
97
98
A.
B.
C.
D.
二、多选题
9.下面的四个问题中,可以用抽样调查方法的是(
)
A.武汉火神山医院供应库房工作人员对新入库的万只一次性医用口罩进行质检
B.中国银行兰山分行对天元公司万元存款的现钞的真假检验
C.空降兵战士检查个伞包及伞的质量
D.一汽大众质检部门检验最新一批斯柯达汽车的防碰撞性能
10.国家为了实现经济“双循环”大战略,对东部和西部地区的多个县市的某一类经济指标进行调查,得出东部,西部两组数据的茎叶图如图所示,则下列结论正确的是(
)
A.西部的平均数为13.3
B.东部的极差小于西部的极差
C.东部的30%分位数是11.6
D.东部的众数比西部的众数小
11.甲?乙?丙三位同学在一项集训中的40次测试分数都在内,将他们的测试分数分别绘制成频率分布直方图(如图所示),记甲?乙?丙的分数标准差分别为,则它们的大小关系为(
)
A.
B.
C.
D.
12.为普及疫情知识,某校不定期地共组织了10次全员性的防控知识问答竞赛,下面是甲、乙两个班级10次成绩Y(单位:分)的折线图:根据折线图( )
A.甲班的成绩分数呈上升趋势
B.甲班乙班的成绩分数平均值均为7
C.甲班成绩分数的方差大于乙班成绩分数的方差
D.从第7次到第10次甲班成绩分数增量大于乙班成绩分数増量
13.某地区城乡居民储蓄存款年底余额(单位:亿元)变化情况如图所示,下列判断一定正确的是(
)
A.该地区城乡居民储蓄存款年底余额总数逐年上升
B.到年农村居民存款年底总余额已超过了城镇居民存款年底总余额
C.城镇居民存款年底余额逐年下降
D.年城乡居民存款年底余额增长率大约为
14.雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法,为比较甲,乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,
则下面叙述正确的是(
)
A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观直观想象想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
三、填空题
15.高二年级共有学生600人,采用分层随机抽样的方法从男生中抽取20人,得到其平均身高数据为172.5cm;从女生中抽取18人,得到其平均身高数据为162cm,则高二年级学生的平均身高估计值为___________.
16.在用抽签法抽样时,有下列五个步骤:
(1)从箱中每次抽出1个号签,并记录其编号,连续抽取k次;
(2)将总体中的所有个体编号;
(3)制作号签;
(4)将总体中与抽到的签的编号相一致的个体取出构成样本;
(5)将号签放在同一箱中,并搅拌均匀.
以上步骤的次序是______________.
17.下列调查中:①考察一片经济林中树木的平均直径;②疫情开学前,某市对全体高三教师和学生进行血清抗体检测;③省教育机构调查参加高考模拟考试的60万名考生的英语答题情况;④某市委书记用一上午时间随机到全市高中学校检查高三开学情况.适合用抽样调查方法获取数据的是________.(填序号)
18.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
四、解答题
19.某中学要从高一年级甲、乙两个班级中选择一个班参加市电视台组织的“环保知识竞赛”.该校对甲、乙两班的参赛选手(每班7人)进行了一次环境知识测试,他们取得的成绩的茎叶图如图所示,其中甲班学生的平均分是85分,乙班学生成绩的中位数是85.
(1)求的值;
(2)根据茎叶图,求甲、乙两班同学成绩的方差的大小,并从统计学角度分析,该校应选择甲班还是乙班参赛.
20.年,面对突如其来的新冠肺炎疫情冲击,在党中央领导下,各地区各部门统筹疫情防控和经济社会发展取得显著成效,商业模式创新发展,消费结构升级持续发展.某主打线上零售产品的企业随机抽取了名销售员,统计了其年的月均销售额(单位:万元),将数据按照分成组,制成了如图所示的频率分布直方图.已知组的频数比组多.
(1)求频率分布直方图中和的值;
(2)该企业为了挖掘销售员的工作潜力,对销售员实行冲刺目标管理,即给销售员确定一个具体的冲刺目标,完成这个冲刺目标,则给予额外的奖励,若公司希望恰有的销售人员能够获得额外奖励,求该企业应该制定的月销售冲刺目标值.
21.甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
22.我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为,,,,,其频率分布直方图如图所示,请你解答下列问题:
(1)求的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
23.某家水果店的店长为了解本店苹果的日销售情况,记录了近期连续120天苹果的日销售量(单位:),并绘制频率分布直方图如下:
(1)请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数;(同一组中的数据以这组数据所在区间中点的值作代表)
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在10天中,大约有8天可以满足顾客的需求).请问每天应该进多少千克苹果?(精确到整数位)
参考答案
1.B
解:日均垃圾量不少于14吨的组为和,频率和为,
则个,
故选:B.
2.D
对于A:由图可知显然正确;
对于C:由图可知,副食的销售额占比为:,故C正确;
对于B:由副食的销售额和占比可得商场一天总的营业额为:元,故服装鞋帽和百货日杂的销售额为:元,故B正确;
对于D:由图不能得出,故D错误.
故选:D.
3.C
解:对于A,2011—2016年中国发明专利量逐年增长,所以A正确;
对于B,2019年中国发明专利量为1458件,比2018年减了,所以B正确;
对于C,由图表易知2016年之后三类专利申请总量确实在逐年下滑,但实用新型专利量和外观专利量却在逐年增长,所以C不正确;
对于D,2011年中国实用新型专利在三类专利申请总量中占,所以D正确.
故选:C
4.B
利用随机数表从第行第列开始向右读取,依次为09,84(去除),96(去除),57(去除),,09(重复,去除),84(去除),73(去除),03,所以抽取的第个个体的编号是03.
故选:B.
5.D
由题意得,①,,②
由①②解得或,所以|x-y|=18.
故选:D.
6.C
解:∵360∶280∶200=9∶7∶5,
∴甲付×65=27
(钱),乙付×65=21
(钱),丙付×65=15
(钱),则C说法错误.
故选:C.
7.D
实线的数字为:,
虚线的数字为:,
所以,
,
.
故选:D
8.C
由表格中的数据可知,,
由频率分布直方图可知,,,
则.
故选:C.
9.AD
对于A选项,万只一次性医用口罩容量很大,应采用抽样调查的方法;
对于B选项,万元存款的现钞的真假检验必须普查,不能放过任何一张假钞;
对于C选项,伞包以伞的质量决定人的生命,必须普查;
对于D选项,防碰撞性能的检测会对产品产生破坏,应采取抽样调查的方法.
故选:AD.
10.ACD
解:对于A:即西部的平均数为13.3,故A正确;
对于B:东部的最大值为,最小值为,极差为;西部的最大值为,最小值为,极差为;故B错误;
对于C:东部共13个数据,,即从小到大的第4个数为东部的30%分位数,所以东部的30%分位数是11.6,故C正确;
对于D:东部的众数为,西部的众数为和均大于,故D正确;
故选:ACD
11.AB
解:根据三个频率分布直方图知,
第一组数据的两端数字较多,绝大部分数字都处在两端数据偏离平均数远,最分散,其方差最大;
第二组数据绝大部分数字都在平均数左右,数据最集中,其方差最小;
第三组数据是单峰的每一个小长方形的差别比较小,数字分布均匀,
数据不如第一组偏离平均数大,方差比第一组中数据中的方差小,比第二组数据方差大;
综上可知.
故选:.
12.ABCD
对于A,由频率分布折线图知,甲班的成绩分数呈上升趋势,A正确;
对于B,计算甲班成绩平均值为
,
计算乙班成绩平均值为,所以甲班乙班的成绩分数平均值均为7,故B正确;
对于C,根据甲班成绩数据比乙班成绩数据波动性更大些,所以甲班方差比乙班方差大些,故C正确;
对于D,由频率分布折线图知,从第7次到第10次甲班成绩分数增量大于乙班成绩分数增量,故D正确.
故选:
ABCD.
13.AD
由条形图可知,余额总数逐年上升,故A项正确;由城乡储蓄构成百分比可知,年农村居民存款年底总余额占,城镇居民存款年底总余额占,没有超过,故B项错误;城镇居民存款年底余额所占的比重逐年下降,但城镇居民存款年底余额年,年,年分别为(亿元),(亿元),(亿元),总体不是逐年下降的,故C项错误,年城乡居民存款年底余额增长率大约为,故D项正确.
故选:AD.
14.AC
A选项,由雷达图可知,甲的逻辑推理能力指标值4优于乙的逻辑推理能力指标值3,即A正确;
B选项,由雷达图可知,甲的数学建模能力指标值3低于乙的直观直观想象想象能力指标值4,故B错;
C选项,由雷达图可知,乙的数据分析、数学抽象、数学建模指标都优于甲;甲乙的直观想象指标相同;甲的逻辑推理、数学运算指标优于乙;因此乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平,即C正确;
D选项,由雷达图可知,甲的数学运算能力指标值4低于甲的直观想象能力指标值5,即D错;
故选:AC.
15.167.5cm
由题意可得高二年级学生的平均身高估计值为.
故答案为:167.5cm.
16.(2)(3)(5)(1)(4)
利用抽签法第一步要进行编号,然后做号签,放入容器,接下来按照逐个不放回地抽取号签,最后将与编号一致的个体取出构成样本,故这些步骤的先后顺序为(2)(3)(5)(1)(4).
故答案为:(2)(3)(5)(1)(4).
17.①③④
①该问题用普查的方法很难实现,适合用抽样调查的方法获取数据;②检测必须要知道每一位老师和学生是否正常,不能用抽样调查的方法获取数据;③60万名考生的答题情况用普查的方法获取数据不合适,适合用抽样调查的方法获取数据;④一上午时间,市委书记无法检查到全市每一所高中学校,该问题只能用抽样调查的方法获取数据.
故答案为:①③④
18.
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
19(1);(2)应该选择乙班参赛
解:(1)因为甲班学生的平均分是85,
所以,
解得.
因为乙班学生成绩的中位数是85,所以.
(2)由(1)可知,,
所以
.
由茎叶图可得,,
所以
,
所以.
20.(1),;(2)万元.
(1)由题意得,
解得,.
(2)设应该制定的月销售冲刺目标值为万元,则在频率分布直方图中右边的面积为.
最后一组的面积是,
最后两组的面积之和为.
因为,所以位于倒数第二组,
则,解得.
所以该企业的月销售冲刺目标值应该定为万元.
21.
(1)由图象可得甲、乙两人五次测试的成绩分别为
甲:10分,13分,12分,14分,16分;
乙:13分,14分,12分,12分,14分.
=13,
=13,
×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,
×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.
(2)由可知乙的成绩较稳定.
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.
22(1)
(2)60人
(3)76分
(1)由,解得
(2)学生成绩在之间的频率为0.05,
故可估计所有参赛学生中能获奖的人数约为人
(3)平均分的估计值为:分
23.(1)众数为为85,平均数为;(2)每天应该进98千克苹果.
(1)如图示:区间频率最大,所以众数为85,
平均数为:
(2)日销售量[60,90)的频率为,日销量[60,100)的频率为,
故所求的量位于
由得
故每天应该进98千克苹果.
试卷第1页,总3页
一、单选题
1.某市通过统计50个大型社区产生的日均垃圾量,绘制了如下图所示的频率分布直方图,数据的分组依次为:,,,,,,.为了鼓励率先实施垃圾分类回收,将日均垃圾量不少于14吨的社区划定为试点社区,则这样的试点社区个数是(
).
A.4
B.10
C.19
D.40
2.如图为某商场一天营业额的扇形统计图,根据统计图你不能得出的信息为(
)
A.该商场家用电器销售额为全商场营业额的40%
B.服装鞋帽和百货日杂共售出29000元
C.副食的销售额为该商场营业额的10%
D.家用电器部所得利润最高
3.如图为2011—2019年中国白酒行业各类型专利申请情况.
根据图中数据,下列说法不正确的是(
)
A.2011-2016年中国发明专利量逐年增长
B.2019年中国发明专利量为1458件,约比2018年减少了44.22%
C.2016年之后,白酒行业专利申请总量出现下滑,且实用新型专利量、发明专利量、外观专利量也在逐年下滑
D.2011年中国实用新型专利量在三类专利申请总量中约占7.69%
4.总体由编号为的个个体组成,利用随机数表从中抽取个个体,下面提供随机数表的第行到第行:
若从表中第行第列开始向右依次读取,则抽取的第个个体的编号是(
)
A.
B.
C.
D.
4.高三学生李丽在一年的五次数学模拟考试中的成绩(单位:分)为x,y,105,109,110.已知她的五次数学成绩数据的平均数为108分,方差为35.2,则|x-y|的值为(
)
A.15
B.16
C.17
D.18
6.分层随机抽样是将总体分成互不交叉的层,然后按照一定的比例,从各层独立地抽取一定数量的个体,组成一个样本的抽样方法.在《九章算术》第三章“衰分”中有如下问题:“今有甲持钱三百六十,乙持钱二百八十,丙持钱二百,凡三人俱出关,关税六十五钱.欲以钱多少衰出之,问各几何?”其译文为:今有甲持360钱,乙持280钱,丙持200钱,甲、乙、丙三人一起出关,关税共65钱,要按照各人带多少的比例进行交税,问三人各应付多少税?下列说法错误的是(
)
A.甲应付27钱
B.乙应付21钱
C.丙应付15钱
D.三者中甲付的钱最多,丙付的钱最少
7.甲、乙两名射击运动爱好者在相同条件下各射击次,中靶环数情况如图所示.则甲、乙两人中靶环数的方差分别为(
)
A.,
B.,
C.,
D.,
8.“脱口秀大赛”上选手的分数分为观众评分和嘉宾评分.组织方将观众评分按照,,分组,绘制频率分布直方图如图所示.嘉宾评分的平均数为,观众评分的平均数为,中位数为,则下列选项正确的是(
)
嘉宾
评分
96
97
96
89
97
98
A.
B.
C.
D.
二、多选题
9.下面的四个问题中,可以用抽样调查方法的是(
)
A.武汉火神山医院供应库房工作人员对新入库的万只一次性医用口罩进行质检
B.中国银行兰山分行对天元公司万元存款的现钞的真假检验
C.空降兵战士检查个伞包及伞的质量
D.一汽大众质检部门检验最新一批斯柯达汽车的防碰撞性能
10.国家为了实现经济“双循环”大战略,对东部和西部地区的多个县市的某一类经济指标进行调查,得出东部,西部两组数据的茎叶图如图所示,则下列结论正确的是(
)
A.西部的平均数为13.3
B.东部的极差小于西部的极差
C.东部的30%分位数是11.6
D.东部的众数比西部的众数小
11.甲?乙?丙三位同学在一项集训中的40次测试分数都在内,将他们的测试分数分别绘制成频率分布直方图(如图所示),记甲?乙?丙的分数标准差分别为,则它们的大小关系为(
)
A.
B.
C.
D.
12.为普及疫情知识,某校不定期地共组织了10次全员性的防控知识问答竞赛,下面是甲、乙两个班级10次成绩Y(单位:分)的折线图:根据折线图( )
A.甲班的成绩分数呈上升趋势
B.甲班乙班的成绩分数平均值均为7
C.甲班成绩分数的方差大于乙班成绩分数的方差
D.从第7次到第10次甲班成绩分数增量大于乙班成绩分数増量
13.某地区城乡居民储蓄存款年底余额(单位:亿元)变化情况如图所示,下列判断一定正确的是(
)
A.该地区城乡居民储蓄存款年底余额总数逐年上升
B.到年农村居民存款年底总余额已超过了城镇居民存款年底总余额
C.城镇居民存款年底余额逐年下降
D.年城乡居民存款年底余额增长率大约为
14.雷达图是以从同一点开始的轴上表示的三个或更多个定量变量的二维图表的形式显示多变量数据的图形方法,为比较甲,乙两名学生的数学学科素养的各项能力指标值(满分为5分,分值高者为优),绘制了如图所示的六维能力雷达图,例如图中甲的数学抽象指标值为4,乙的数学抽象指标值为5,
则下面叙述正确的是(
)
A.甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值
B.甲的数学建模能力指标值优于乙的直观直观想象想象能力指标值
C.乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平
D.甲的数学运算能力指标值优于甲的直观想象能力指标值
三、填空题
15.高二年级共有学生600人,采用分层随机抽样的方法从男生中抽取20人,得到其平均身高数据为172.5cm;从女生中抽取18人,得到其平均身高数据为162cm,则高二年级学生的平均身高估计值为___________.
16.在用抽签法抽样时,有下列五个步骤:
(1)从箱中每次抽出1个号签,并记录其编号,连续抽取k次;
(2)将总体中的所有个体编号;
(3)制作号签;
(4)将总体中与抽到的签的编号相一致的个体取出构成样本;
(5)将号签放在同一箱中,并搅拌均匀.
以上步骤的次序是______________.
17.下列调查中:①考察一片经济林中树木的平均直径;②疫情开学前,某市对全体高三教师和学生进行血清抗体检测;③省教育机构调查参加高考模拟考试的60万名考生的英语答题情况;④某市委书记用一上午时间随机到全市高中学校检查高三开学情况.适合用抽样调查方法获取数据的是________.(填序号)
18.某社会爱心组织面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取名按年龄分组:第组,第组,第组,第组,第组,得到的频率分布直方图如图所示.若从第,,组中用分层抽样的方法抽取名志愿者参与广场的宣传活动,应从第组抽取__________名志愿者.
四、解答题
19.某中学要从高一年级甲、乙两个班级中选择一个班参加市电视台组织的“环保知识竞赛”.该校对甲、乙两班的参赛选手(每班7人)进行了一次环境知识测试,他们取得的成绩的茎叶图如图所示,其中甲班学生的平均分是85分,乙班学生成绩的中位数是85.
(1)求的值;
(2)根据茎叶图,求甲、乙两班同学成绩的方差的大小,并从统计学角度分析,该校应选择甲班还是乙班参赛.
20.年,面对突如其来的新冠肺炎疫情冲击,在党中央领导下,各地区各部门统筹疫情防控和经济社会发展取得显著成效,商业模式创新发展,消费结构升级持续发展.某主打线上零售产品的企业随机抽取了名销售员,统计了其年的月均销售额(单位:万元),将数据按照分成组,制成了如图所示的频率分布直方图.已知组的频数比组多.
(1)求频率分布直方图中和的值;
(2)该企业为了挖掘销售员的工作潜力,对销售员实行冲刺目标管理,即给销售员确定一个具体的冲刺目标,完成这个冲刺目标,则给予额外的奖励,若公司希望恰有的销售人员能够获得额外奖励,求该企业应该制定的月销售冲刺目标值.
21.甲、乙二人参加某体育项目训练,近期的五次测试成绩得分情况如图所示.
(1)分别求出两人得分的平均数与方差;
(2)根据图和上面算得的结果,对两人的训练成绩作出评价.
22.我校举行“两城同创”的知识竞赛答题,高一年级共有1200名学生参加了这次竞赛.为了解竞赛成绩情况,从中抽取了100名学生的成绩进行统计.其中成绩分组区间为,,,,,其频率分布直方图如图所示,请你解答下列问题:
(1)求的值;
(2)若成绩不低于90分的学生就能获奖,问所有参赛学生中获奖的学生约为多少人;
(3)根据频率分布直方图,估计这次平均分(用组中值代替各组数据的平均值).
23.某家水果店的店长为了解本店苹果的日销售情况,记录了近期连续120天苹果的日销售量(单位:),并绘制频率分布直方图如下:
(1)请根据频率分布直方图估计该水果店苹果日销售量的众数和平均数;(同一组中的数据以这组数据所在区间中点的值作代表)
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求.店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在10天中,大约有8天可以满足顾客的需求).请问每天应该进多少千克苹果?(精确到整数位)
参考答案
1.B
解:日均垃圾量不少于14吨的组为和,频率和为,
则个,
故选:B.
2.D
对于A:由图可知显然正确;
对于C:由图可知,副食的销售额占比为:,故C正确;
对于B:由副食的销售额和占比可得商场一天总的营业额为:元,故服装鞋帽和百货日杂的销售额为:元,故B正确;
对于D:由图不能得出,故D错误.
故选:D.
3.C
解:对于A,2011—2016年中国发明专利量逐年增长,所以A正确;
对于B,2019年中国发明专利量为1458件,比2018年减了,所以B正确;
对于C,由图表易知2016年之后三类专利申请总量确实在逐年下滑,但实用新型专利量和外观专利量却在逐年增长,所以C不正确;
对于D,2011年中国实用新型专利在三类专利申请总量中占,所以D正确.
故选:C
4.B
利用随机数表从第行第列开始向右读取,依次为09,84(去除),96(去除),57(去除),,09(重复,去除),84(去除),73(去除),03,所以抽取的第个个体的编号是03.
故选:B.
5.D
由题意得,①,,②
由①②解得或,所以|x-y|=18.
故选:D.
6.C
解:∵360∶280∶200=9∶7∶5,
∴甲付×65=27
(钱),乙付×65=21
(钱),丙付×65=15
(钱),则C说法错误.
故选:C.
7.D
实线的数字为:,
虚线的数字为:,
所以,
,
.
故选:D
8.C
由表格中的数据可知,,
由频率分布直方图可知,,,
则.
故选:C.
9.AD
对于A选项,万只一次性医用口罩容量很大,应采用抽样调查的方法;
对于B选项,万元存款的现钞的真假检验必须普查,不能放过任何一张假钞;
对于C选项,伞包以伞的质量决定人的生命,必须普查;
对于D选项,防碰撞性能的检测会对产品产生破坏,应采取抽样调查的方法.
故选:AD.
10.ACD
解:对于A:即西部的平均数为13.3,故A正确;
对于B:东部的最大值为,最小值为,极差为;西部的最大值为,最小值为,极差为;故B错误;
对于C:东部共13个数据,,即从小到大的第4个数为东部的30%分位数,所以东部的30%分位数是11.6,故C正确;
对于D:东部的众数为,西部的众数为和均大于,故D正确;
故选:ACD
11.AB
解:根据三个频率分布直方图知,
第一组数据的两端数字较多,绝大部分数字都处在两端数据偏离平均数远,最分散,其方差最大;
第二组数据绝大部分数字都在平均数左右,数据最集中,其方差最小;
第三组数据是单峰的每一个小长方形的差别比较小,数字分布均匀,
数据不如第一组偏离平均数大,方差比第一组中数据中的方差小,比第二组数据方差大;
综上可知.
故选:.
12.ABCD
对于A,由频率分布折线图知,甲班的成绩分数呈上升趋势,A正确;
对于B,计算甲班成绩平均值为
,
计算乙班成绩平均值为,所以甲班乙班的成绩分数平均值均为7,故B正确;
对于C,根据甲班成绩数据比乙班成绩数据波动性更大些,所以甲班方差比乙班方差大些,故C正确;
对于D,由频率分布折线图知,从第7次到第10次甲班成绩分数增量大于乙班成绩分数增量,故D正确.
故选:
ABCD.
13.AD
由条形图可知,余额总数逐年上升,故A项正确;由城乡储蓄构成百分比可知,年农村居民存款年底总余额占,城镇居民存款年底总余额占,没有超过,故B项错误;城镇居民存款年底余额所占的比重逐年下降,但城镇居民存款年底余额年,年,年分别为(亿元),(亿元),(亿元),总体不是逐年下降的,故C项错误,年城乡居民存款年底余额增长率大约为,故D项正确.
故选:AD.
14.AC
A选项,由雷达图可知,甲的逻辑推理能力指标值4优于乙的逻辑推理能力指标值3,即A正确;
B选项,由雷达图可知,甲的数学建模能力指标值3低于乙的直观直观想象想象能力指标值4,故B错;
C选项,由雷达图可知,乙的数据分析、数学抽象、数学建模指标都优于甲;甲乙的直观想象指标相同;甲的逻辑推理、数学运算指标优于乙;因此乙的六维能力指标值整体水平优于甲的六维能力指标值整体水平,即C正确;
D选项,由雷达图可知,甲的数学运算能力指标值4低于甲的直观想象能力指标值5,即D错;
故选:AC.
15.167.5cm
由题意可得高二年级学生的平均身高估计值为.
故答案为:167.5cm.
16.(2)(3)(5)(1)(4)
利用抽签法第一步要进行编号,然后做号签,放入容器,接下来按照逐个不放回地抽取号签,最后将与编号一致的个体取出构成样本,故这些步骤的先后顺序为(2)(3)(5)(1)(4).
故答案为:(2)(3)(5)(1)(4).
17.①③④
①该问题用普查的方法很难实现,适合用抽样调查的方法获取数据;②检测必须要知道每一位老师和学生是否正常,不能用抽样调查的方法获取数据;③60万名考生的答题情况用普查的方法获取数据不合适,适合用抽样调查的方法获取数据;④一上午时间,市委书记无法检查到全市每一所高中学校,该问题只能用抽样调查的方法获取数据.
故答案为:①③④
18.
第3组的人数为,
第4组的人数为,
第5组的人数为,
所以这三组共有60名志愿者,
所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,第三组应抽取名,
故答案为:3.
19(1);(2)应该选择乙班参赛
解:(1)因为甲班学生的平均分是85,
所以,
解得.
因为乙班学生成绩的中位数是85,所以.
(2)由(1)可知,,
所以
.
由茎叶图可得,,
所以
,
所以.
20.(1),;(2)万元.
(1)由题意得,
解得,.
(2)设应该制定的月销售冲刺目标值为万元,则在频率分布直方图中右边的面积为.
最后一组的面积是,
最后两组的面积之和为.
因为,所以位于倒数第二组,
则,解得.
所以该企业的月销售冲刺目标值应该定为万元.
21.
(1)由图象可得甲、乙两人五次测试的成绩分别为
甲:10分,13分,12分,14分,16分;
乙:13分,14分,12分,12分,14分.
=13,
=13,
×[(10-13)2+(13-13)2+(12-13)2+(14-13)2+(16-13)2]=4,
×[(13-13)2+(14-13)2+(12-13)2+(12-13)2+(14-13)2]=0.8.
(2)由可知乙的成绩较稳定.
从折线图看,甲的成绩基本呈上升状态,而乙的成绩上下波动,可知甲的成绩在不断提高,而乙的成绩则无明显提高.
22(1)
(2)60人
(3)76分
(1)由,解得
(2)学生成绩在之间的频率为0.05,
故可估计所有参赛学生中能获奖的人数约为人
(3)平均分的估计值为:分
23.(1)众数为为85,平均数为;(2)每天应该进98千克苹果.
(1)如图示:区间频率最大,所以众数为85,
平均数为:
(2)日销售量[60,90)的频率为,日销量[60,100)的频率为,
故所求的量位于
由得
故每天应该进98千克苹果.
试卷第1页,总3页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
