2021-2022学年人教版八年级数学上册11.3多边形及其内角和能力提升训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.3多边形及其内角和能力提升训练(word版、含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 153.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 20:48:34 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学上册《11.3多边形及其内角和》能力提升训练(附答案)
一.多边形
1.下列图形不具有稳定性的是( )
A.正方形
B.等腰三角形
C.直角三角形
D.钝角三角形
2.下列图形中具有稳定性的是( )
A.正六边形
B.五边形
C.平行四边形
D.钝角三角形
3.如图,五边形ABCDE中,AB=BC=5,AE=ED=6,∠ABC+∠AED=180°,M为边CD的中点,BM=7,EM=8,则五边形ABCDE的面积为
.
二.多边形内角与外角
4.一个多边形的内角和是720°,这个多边形是( )
A.五边形
B.六边形
C.七边形
D.八边形
5.已知,正n边形的每一个内角是144°,则n的值是( )
A.6
B.8
C.10
D.12
6.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )
A.8
B.9
C.10
D.11
7.已知在四边形ABCD中,∠A=∠C=90°.如图,∠EDN=n∠CDE,∠EBM=n∠CBE(n>2);则∠BED的度数为( )
A.90°﹣
B.90°﹣
C.60°﹣
D.60°﹣
8.下列说法中,正确的个数有( )
①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°;
③三角形的外角大于与它不相邻的任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°.
A.1个
B.2个
C.3个
D.4个
9.小明在计算多边形内角和时,把其中一个内角多加了一次,得到内角和为500o,则多加的这个内角的大小为
.
10.如果一个正多边形的一个内角是162°,则这个正多边形是正
边形.
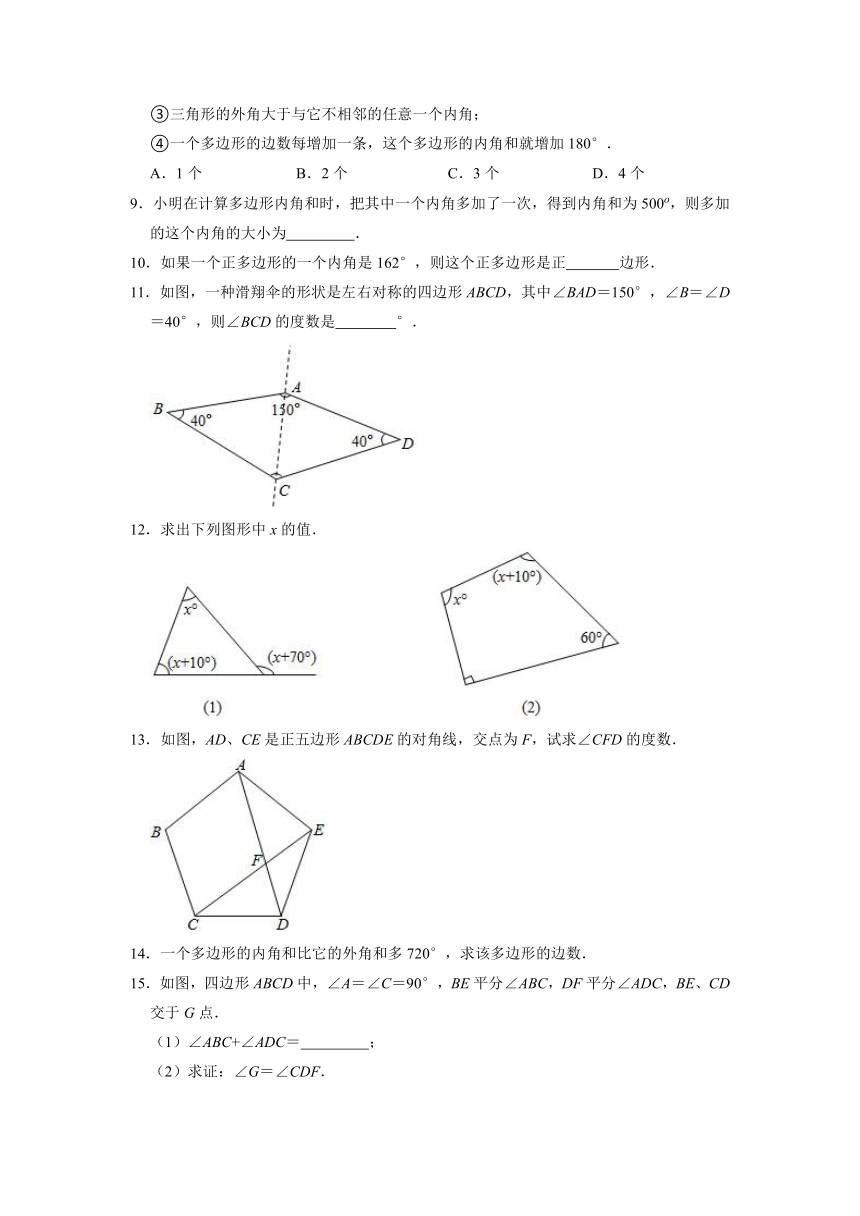
11.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,∠B=∠D=40°,则∠BCD的度数是
°.
12.求出下列图形中x的值.
13.如图,AD、CE是正五边形ABCDE的对角线,交点为F,试求∠CFD的度数.
14.一个多边形的内角和比它的外角和多720°,求该多边形的边数.
15.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE、CD交于G点.
(1)∠ABC+∠ADC=
;
(2)求证:∠G=∠CDF.
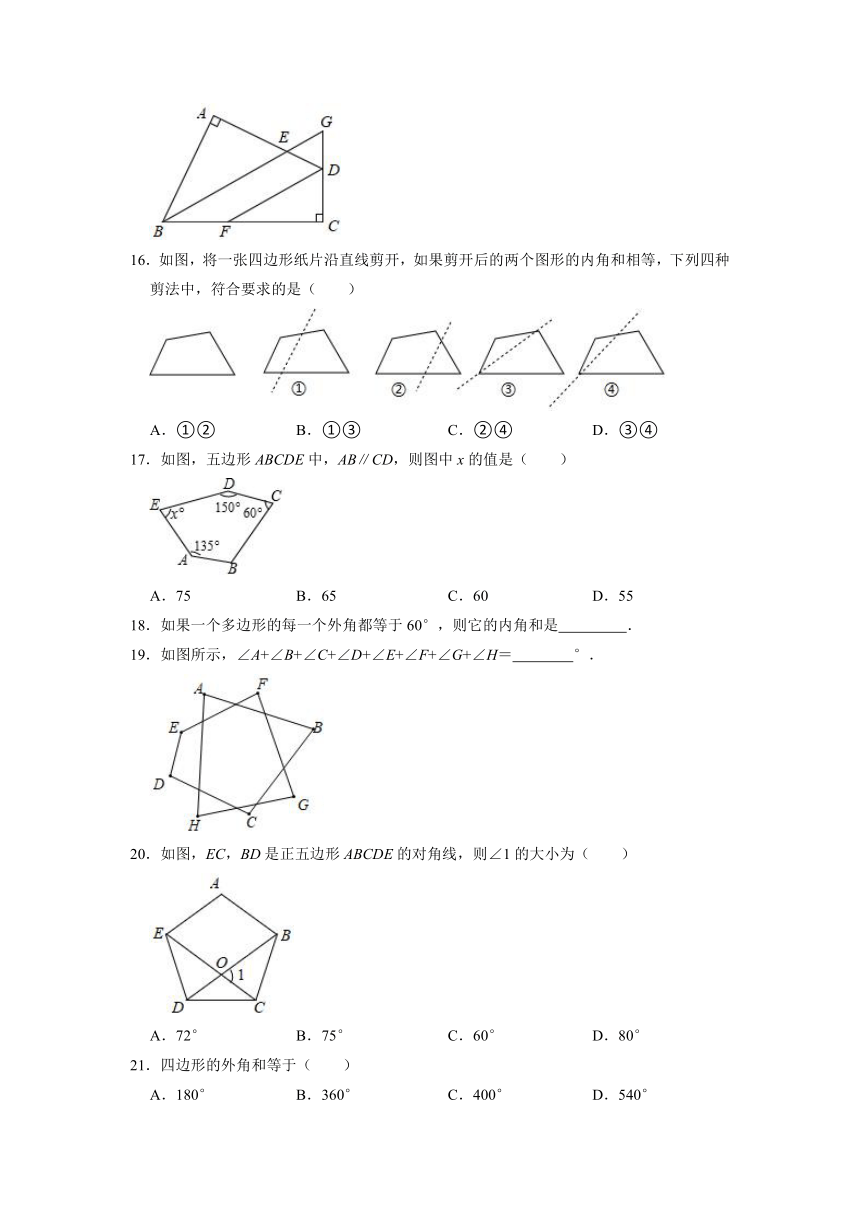
16.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①②
B.①③
C.②④
D.③④
17.如图,五边形ABCDE中,AB∥CD,则图中x的值是( )
A.75
B.65
C.60
D.55
18.如果一个多边形的每一个外角都等于60°,则它的内角和是
.
19.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
°.
20.如图,EC,BD是正五边形ABCDE的对角线,则∠1的大小为( )
A.72°
B.75°
C.60°
D.80°
21.四边形的外角和等于( )
A.180°
B.360°
C.400°
D.540°
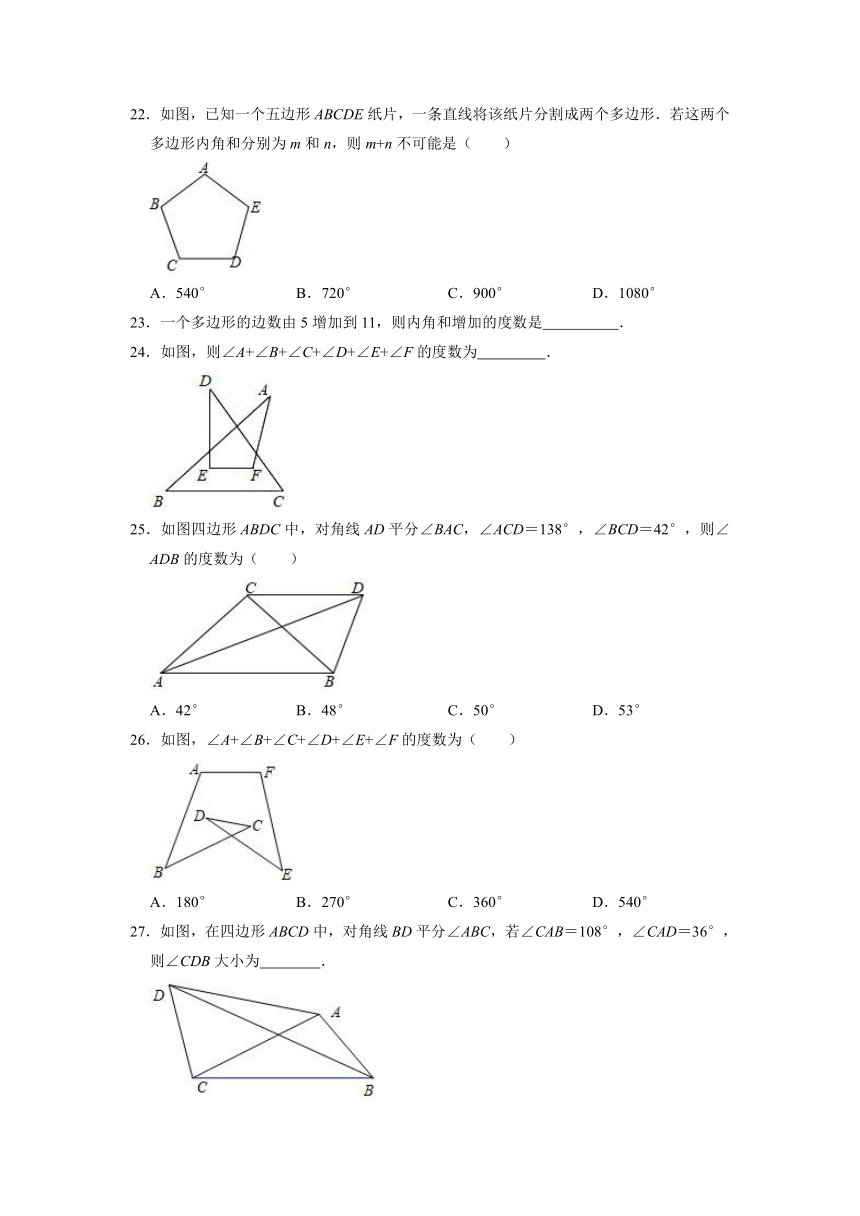
22.如图,已知一个五边形ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为m和n,则m+n不可能是( )
A.540°
B.720°
C.900°
D.1080°
23.一个多边形的边数由5增加到11,则内角和增加的度数是
.
24.如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为
.
25.如图四边形ABDC中,对角线AD平分∠BAC,∠ACD=138°,∠BCD=42°,则∠ADB的度数为( )
A.42°
B.48°
C.50°
D.53°
26.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180°
B.270°
C.360°
D.540°
27.如图,在四边形ABCD中,对角线BD平分∠ABC,若∠CAB=108°,∠CAD=36°,则∠CDB大小为
.
参考答案
一.多边形
1.解:正方形不具有稳定性,故A符合题意;
故选:A.
2.解:正六边形,五边形,平行四边形,钝角三角形中只有钝角三角形具有稳定性.
故选:D.
3.解:如图,延长BM到点F,使FM=BM,连接BE,EF,DF,
在△BMC和△FDM中,
,
∴△BMC≌△FDM(SAS),
∴BC=DF=AB,∠C=∠CDF,
∵∠A+∠ABC+∠C+∠CDE+∠AED=(5﹣2)×180°=540°,
∵∠ABC+∠AED=180°,
∴∠A+∠C+∠CDE=360°,
∵∠CDE+∠CDF+∠EDF=360°,
∴∠A=∠EDF,
在△ABE和△DFE中,
,
∴ABE≌△DFE(SAS),
∴BE=EF,
∵BM=MF,
∴EM⊥BF,
∴五边形ABCDE的面积=S△ABE+S△BCM+S四BMDE
=S△EDF+S△MDF+S四BMDE
=S△BEF
=BF?EM
=×7×2×8
=56.
故答案为:56.
二.多边形内角与外角
4.解:设这个多边形的边数为n,由题意,得
(n﹣2)180°=720°,
解得:n=6,
故这个多边形是六边形.
故选:B.
5.解:∵正n边形的每一个内角都等于144°,
∴每一个外角都是180﹣144=36(度),
∴n=360÷36=10.
故选:C.
6.解:1500÷180=8,
则正多边形的边数是8+1+2=11.
故选:D.
7.解:延长DC交BE于点H,
∵∠A=∠BCD=90°,
∴∠ABC+∠ADC=180°,
∴∠CDN+∠CBM=180°,
∵∠EDN=n∠CDE,∠EBM=n∠CBE
∴∠CDE+∠CBE=×180°=,
由三角形的外角性质得,∠BHD=∠CDE+∠BED,∠BCD=∠BHD+∠CBE,
∴∠BCD=∠CBE+∠CDE+∠BED,
∴∠BED=∠BCD﹣(∠CBE+∠CDE)=90°﹣,
故选:A.
8.解:①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形,说法错误;改正为:若任意两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°,说法正确;
③三角形的外角大于与它不相邻的任意一个内角,说法正确;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°,说法正确.
所以正确的个数有3个.
故选:C.
9.解:设多边形的边数为n,多加的内角度数为α,则
(n﹣2)?180°=500°﹣α,
∵500°=2×180°+140°,多边形内角和应是180°的倍数,
∴同学多加的一个内角为140°.
故答案为:140°.
10.解:∵正多边形的一个内角是162°,
∴它的外角是:180°﹣162°=18°,
边数n=360°÷18°=20.
故答案为:二十.
11.解:∵一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠D=∠B=40°,
∴∠BCD=360°﹣150°﹣40°﹣40°=130°.
故答案为:130.
12.解:(1)由三角形的外角性质得,x+(x+10)=x+70,
即2x+10=x+70,
解得,x=60.
(2)根据四边形的内角和为360°得,
x+(x+10)+90+60=360,
解得,x=100.
13.解:∵正五边形ABCDE,
∴CD=DE=AE,∠AED=∠CDE==108°,
∴=36°=∠CED,
∴∠CFD=∠ADE+∠CED=36°+36°=72°.
14.解:∵一个多边形的内角和比它的外角和多720°,
∴这个多边形的内角和为360°+720°=1080°,
设这个多边形的边数为n,
则(n﹣2)?180°=1080°,
解得n=8,
答:该多边形的边数为8.
15.证明:(1)∵四边形ABCD中,∠A=∠C=90°,∠A+∠ABC+∠C+∠ADC=360°,
∴∠ABC+∠ADC=180°;
故答案为:180°;
(2)∵BE平分∠ABC,DF平分∠ADC,
∴∠GBC=∠ABC,∠CDF=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠GBC+∠CDF=90°,
∵∠C+∠CDF+∠DFC=180°,∠C=90°,
∴∠CDF+∠DFC=90°,
∴∠GBC=∠DFC,
∴BG∥DF,
∴∠G=∠CDF.
16.解:∵①剪开后的两个图形是四边形,它们的内角和都是360°,③剪开后的两个图形是三角形,它们的内角和都是180°;
∴①③剪开后的两个图形的内角和相等,
故选:B.
17.解:∵AB∥CD,
∴∠B=180°﹣∠C=180°﹣60°=120°,
∵五边形ABCDE内角和为(5﹣2)×180°=540°,
∴在五边形ABCDE中,∠E=540°﹣135°﹣120°﹣60°﹣150°=75°.
故图中x的值是75.
故选:A.
18.解:多边形边数为:360°÷60°=6,
则这个多边形是六边形;
∴内角和是:(6﹣2)?180°=720°.
故答案为:720°.
19.解:如图,
∵∠A+∠B+∠C+∠1=360°,∠F+∠G+∠H+∠2=360°,∠E+∠D+∠3+∠4=360°,
∠2+∠3=180°,∠1+∠4=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°×3﹣∠1﹣∠2﹣∠3﹣∠4=360°×3﹣180°×2=720°,
故答案为:720.
20.解:∵五边形ABCDE为正五边形,
∴BC=CD=DE,∠BCD=∠CDE=108°,
∴∠CBD=∠CDB=∠CED=∠DCE==36°,
∴∠1=∠BDC+∠DCE=72°.
故选:A.
21.解:∵多边形外角和等于360°,
∴四边形的外角和等于360°.
故选:B.
22.解:图①中,m+n=180°+720°=900°;
图②中,m+n=180°+360°=540°;
图③中,m+n=180°+540°=720°;
图④中,m+n=360°+540°=900°;
图⑤中,m+n=360°+360°=720°.
故m+n不可能是1080°.
故选:D.
23.解:∵n边形的内角和为(n﹣2)?180°,
∴边数由5增加到11它的内角和增加6×180°=1080°.
故答案为:1080°.
24.解:连接AD,
在△AOD和△BOC中,
∵∠AOD=∠BOC,
∴∠B+∠C=∠1+∠2,
∴∠B+∠C+∠BAF+∠EDF=∠1+∠2+∠BAF+∠EDF=∠EDA+∠FAD,
∵∠EDA+∠FAD+∠E+∠F=360°,
∴∠BAF+∠EDF+∠B+∠C+∠E+∠F=360°,
故答案为:360°.
25.解:如图所示,过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DF=DE,
又∵∠ACD=138°,∠BCD=42°,
∴∠ACB=96°,∠DCF=42°,
∴CD平分∠BCF,
又∵DF⊥AC于F,DG⊥BC于G,
∴DF=DG,
∴DE=DG,
∴BD平分∠CBE,
∴∠DBE=∠CBE,
∵AD平分∠BAC,
∴∠BAD=∠BAC,
∴∠ADB=∠DBE﹣∠BAD=(∠CBE﹣∠BAC)=∠ACB=×96°=48°,
故选:B.
26.解:如图,延长ED交AB于点G,
由三角形外角性质可知:
∠1=∠C+∠CDE,∠2=∠1+∠B,
∴∠2=∠C+∠CDE+∠B,
∴在四边形AFEG中,由四边形内角和可知:
∠A+∠F+∠E+∠2=360°,
∴∠A+∠F+∠E+∠B+∠C+∠CDE=360°.
故选:C.
27.解:过D作DE⊥BA,交BA的延长线于点E,过D作DF⊥BC,交BC的延长线于点F,过D作DH⊥AC,交AC,BC于点H,
∴∠BED=∠BFD,
∵BD平分∠ABC,
∴∠EBD=∠FBD,DE=DF,
在△BDE和△BDF中,
,
∴△BDE≌△BDF(AAS),
∴∠BDE=∠BDF,
∵∠BAC+∠CAD+∠DAE=180°,∠BAC=108°,∠CAD=36°,
∴∠EAD=180°﹣36°﹣108°=36°,
∴∠EAD=∠CAD=36°,
∴∠ADE=∠ADH=90°﹣36°=54°,
∴DE=DH,
∴DF=DH,
∴DC平分∠FDH,
∴∠FDC=∠HDC,
∵∠EBD=∠FBD,
∴∠BAD+∠54°=2∠HDC+54°﹣∠BAD,
解得∠BAD=∠HDC,
∴∠CDB=∠ADH=54°.
故答案为54°.
一.多边形
1.下列图形不具有稳定性的是( )
A.正方形
B.等腰三角形
C.直角三角形
D.钝角三角形
2.下列图形中具有稳定性的是( )
A.正六边形
B.五边形
C.平行四边形
D.钝角三角形
3.如图,五边形ABCDE中,AB=BC=5,AE=ED=6,∠ABC+∠AED=180°,M为边CD的中点,BM=7,EM=8,则五边形ABCDE的面积为
.
二.多边形内角与外角
4.一个多边形的内角和是720°,这个多边形是( )
A.五边形
B.六边形
C.七边形
D.八边形
5.已知,正n边形的每一个内角是144°,则n的值是( )
A.6
B.8
C.10
D.12
6.一个多边形少算一个内角,其余内角之和是1500°,则这个多边形的边数是( )
A.8
B.9
C.10
D.11
7.已知在四边形ABCD中,∠A=∠C=90°.如图,∠EDN=n∠CDE,∠EBM=n∠CBE(n>2);则∠BED的度数为( )
A.90°﹣
B.90°﹣
C.60°﹣
D.60°﹣
8.下列说法中,正确的个数有( )
①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°;
③三角形的外角大于与它不相邻的任意一个内角;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°.
A.1个
B.2个
C.3个
D.4个
9.小明在计算多边形内角和时,把其中一个内角多加了一次,得到内角和为500o,则多加的这个内角的大小为
.
10.如果一个正多边形的一个内角是162°,则这个正多边形是正
边形.
11.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠BAD=150°,∠B=∠D=40°,则∠BCD的度数是
°.
12.求出下列图形中x的值.
13.如图,AD、CE是正五边形ABCDE的对角线,交点为F,试求∠CFD的度数.
14.一个多边形的内角和比它的外角和多720°,求该多边形的边数.
15.如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,BE、CD交于G点.
(1)∠ABC+∠ADC=
;
(2)求证:∠G=∠CDF.
16.如图,将一张四边形纸片沿直线剪开,如果剪开后的两个图形的内角和相等,下列四种剪法中,符合要求的是( )
A.①②
B.①③
C.②④
D.③④
17.如图,五边形ABCDE中,AB∥CD,则图中x的值是( )
A.75
B.65
C.60
D.55
18.如果一个多边形的每一个外角都等于60°,则它的内角和是
.
19.如图所示,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=
°.
20.如图,EC,BD是正五边形ABCDE的对角线,则∠1的大小为( )
A.72°
B.75°
C.60°
D.80°
21.四边形的外角和等于( )
A.180°
B.360°
C.400°
D.540°
22.如图,已知一个五边形ABCDE纸片,一条直线将该纸片分割成两个多边形.若这两个多边形内角和分别为m和n,则m+n不可能是( )
A.540°
B.720°
C.900°
D.1080°
23.一个多边形的边数由5增加到11,则内角和增加的度数是
.
24.如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数为
.
25.如图四边形ABDC中,对角线AD平分∠BAC,∠ACD=138°,∠BCD=42°,则∠ADB的度数为( )
A.42°
B.48°
C.50°
D.53°
26.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
A.180°
B.270°
C.360°
D.540°
27.如图,在四边形ABCD中,对角线BD平分∠ABC,若∠CAB=108°,∠CAD=36°,则∠CDB大小为
.
参考答案
一.多边形
1.解:正方形不具有稳定性,故A符合题意;
故选:A.
2.解:正六边形,五边形,平行四边形,钝角三角形中只有钝角三角形具有稳定性.
故选:D.
3.解:如图,延长BM到点F,使FM=BM,连接BE,EF,DF,
在△BMC和△FDM中,
,
∴△BMC≌△FDM(SAS),
∴BC=DF=AB,∠C=∠CDF,
∵∠A+∠ABC+∠C+∠CDE+∠AED=(5﹣2)×180°=540°,
∵∠ABC+∠AED=180°,
∴∠A+∠C+∠CDE=360°,
∵∠CDE+∠CDF+∠EDF=360°,
∴∠A=∠EDF,
在△ABE和△DFE中,
,
∴ABE≌△DFE(SAS),
∴BE=EF,
∵BM=MF,
∴EM⊥BF,
∴五边形ABCDE的面积=S△ABE+S△BCM+S四BMDE
=S△EDF+S△MDF+S四BMDE
=S△BEF
=BF?EM
=×7×2×8
=56.
故答案为:56.
二.多边形内角与外角
4.解:设这个多边形的边数为n,由题意,得
(n﹣2)180°=720°,
解得:n=6,
故这个多边形是六边形.
故选:B.
5.解:∵正n边形的每一个内角都等于144°,
∴每一个外角都是180﹣144=36(度),
∴n=360÷36=10.
故选:C.
6.解:1500÷180=8,
则正多边形的边数是8+1+2=11.
故选:D.
7.解:延长DC交BE于点H,
∵∠A=∠BCD=90°,
∴∠ABC+∠ADC=180°,
∴∠CDN+∠CBM=180°,
∵∠EDN=n∠CDE,∠EBM=n∠CBE
∴∠CDE+∠CBE=×180°=,
由三角形的外角性质得,∠BHD=∠CDE+∠BED,∠BCD=∠BHD+∠CBE,
∴∠BCD=∠CBE+∠CDE+∠BED,
∴∠BED=∠BCD﹣(∠CBE+∠CDE)=90°﹣,
故选:A.
8.解:①若三条线段中有两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形,说法错误;改正为:若任意两条线段之和大于第三条线段,则以这三条线段为边可作一个三角形;
②一个三角形中,至少有一个角不小于60°,说法正确;
③三角形的外角大于与它不相邻的任意一个内角,说法正确;
④一个多边形的边数每增加一条,这个多边形的内角和就增加180°,说法正确.
所以正确的个数有3个.
故选:C.
9.解:设多边形的边数为n,多加的内角度数为α,则
(n﹣2)?180°=500°﹣α,
∵500°=2×180°+140°,多边形内角和应是180°的倍数,
∴同学多加的一个内角为140°.
故答案为:140°.
10.解:∵正多边形的一个内角是162°,
∴它的外角是:180°﹣162°=18°,
边数n=360°÷18°=20.
故答案为:二十.
11.解:∵一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠D=∠B=40°,
∴∠BCD=360°﹣150°﹣40°﹣40°=130°.
故答案为:130.
12.解:(1)由三角形的外角性质得,x+(x+10)=x+70,
即2x+10=x+70,
解得,x=60.
(2)根据四边形的内角和为360°得,
x+(x+10)+90+60=360,
解得,x=100.
13.解:∵正五边形ABCDE,
∴CD=DE=AE,∠AED=∠CDE==108°,
∴=36°=∠CED,
∴∠CFD=∠ADE+∠CED=36°+36°=72°.
14.解:∵一个多边形的内角和比它的外角和多720°,
∴这个多边形的内角和为360°+720°=1080°,
设这个多边形的边数为n,
则(n﹣2)?180°=1080°,
解得n=8,
答:该多边形的边数为8.
15.证明:(1)∵四边形ABCD中,∠A=∠C=90°,∠A+∠ABC+∠C+∠ADC=360°,
∴∠ABC+∠ADC=180°;
故答案为:180°;
(2)∵BE平分∠ABC,DF平分∠ADC,
∴∠GBC=∠ABC,∠CDF=∠ADC,
∵∠ABC+∠ADC=180°,
∴∠GBC+∠CDF=90°,
∵∠C+∠CDF+∠DFC=180°,∠C=90°,
∴∠CDF+∠DFC=90°,
∴∠GBC=∠DFC,
∴BG∥DF,
∴∠G=∠CDF.
16.解:∵①剪开后的两个图形是四边形,它们的内角和都是360°,③剪开后的两个图形是三角形,它们的内角和都是180°;
∴①③剪开后的两个图形的内角和相等,
故选:B.
17.解:∵AB∥CD,
∴∠B=180°﹣∠C=180°﹣60°=120°,
∵五边形ABCDE内角和为(5﹣2)×180°=540°,
∴在五边形ABCDE中,∠E=540°﹣135°﹣120°﹣60°﹣150°=75°.
故图中x的值是75.
故选:A.
18.解:多边形边数为:360°÷60°=6,
则这个多边形是六边形;
∴内角和是:(6﹣2)?180°=720°.
故答案为:720°.
19.解:如图,
∵∠A+∠B+∠C+∠1=360°,∠F+∠G+∠H+∠2=360°,∠E+∠D+∠3+∠4=360°,
∠2+∠3=180°,∠1+∠4=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°×3﹣∠1﹣∠2﹣∠3﹣∠4=360°×3﹣180°×2=720°,
故答案为:720.
20.解:∵五边形ABCDE为正五边形,
∴BC=CD=DE,∠BCD=∠CDE=108°,
∴∠CBD=∠CDB=∠CED=∠DCE==36°,
∴∠1=∠BDC+∠DCE=72°.
故选:A.
21.解:∵多边形外角和等于360°,
∴四边形的外角和等于360°.
故选:B.
22.解:图①中,m+n=180°+720°=900°;
图②中,m+n=180°+360°=540°;
图③中,m+n=180°+540°=720°;
图④中,m+n=360°+540°=900°;
图⑤中,m+n=360°+360°=720°.
故m+n不可能是1080°.
故选:D.
23.解:∵n边形的内角和为(n﹣2)?180°,
∴边数由5增加到11它的内角和增加6×180°=1080°.
故答案为:1080°.
24.解:连接AD,
在△AOD和△BOC中,
∵∠AOD=∠BOC,
∴∠B+∠C=∠1+∠2,
∴∠B+∠C+∠BAF+∠EDF=∠1+∠2+∠BAF+∠EDF=∠EDA+∠FAD,
∵∠EDA+∠FAD+∠E+∠F=360°,
∴∠BAF+∠EDF+∠B+∠C+∠E+∠F=360°,
故答案为:360°.
25.解:如图所示,过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,
∵AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,
∴DF=DE,
又∵∠ACD=138°,∠BCD=42°,
∴∠ACB=96°,∠DCF=42°,
∴CD平分∠BCF,
又∵DF⊥AC于F,DG⊥BC于G,
∴DF=DG,
∴DE=DG,
∴BD平分∠CBE,
∴∠DBE=∠CBE,
∵AD平分∠BAC,
∴∠BAD=∠BAC,
∴∠ADB=∠DBE﹣∠BAD=(∠CBE﹣∠BAC)=∠ACB=×96°=48°,
故选:B.
26.解:如图,延长ED交AB于点G,
由三角形外角性质可知:
∠1=∠C+∠CDE,∠2=∠1+∠B,
∴∠2=∠C+∠CDE+∠B,
∴在四边形AFEG中,由四边形内角和可知:
∠A+∠F+∠E+∠2=360°,
∴∠A+∠F+∠E+∠B+∠C+∠CDE=360°.
故选:C.
27.解:过D作DE⊥BA,交BA的延长线于点E,过D作DF⊥BC,交BC的延长线于点F,过D作DH⊥AC,交AC,BC于点H,
∴∠BED=∠BFD,
∵BD平分∠ABC,
∴∠EBD=∠FBD,DE=DF,
在△BDE和△BDF中,
,
∴△BDE≌△BDF(AAS),
∴∠BDE=∠BDF,
∵∠BAC+∠CAD+∠DAE=180°,∠BAC=108°,∠CAD=36°,
∴∠EAD=180°﹣36°﹣108°=36°,
∴∠EAD=∠CAD=36°,
∴∠ADE=∠ADH=90°﹣36°=54°,
∴DE=DH,
∴DF=DH,
∴DC平分∠FDH,
∴∠FDC=∠HDC,
∵∠EBD=∠FBD,
∴∠BAD+∠54°=2∠HDC+54°﹣∠BAD,
解得∠BAD=∠HDC,
∴∠CDB=∠ADH=54°.
故答案为54°.
