2021-2022学年八年级数学人教版上册11.2与三角形有关的角优生辅导训练(word版、含解析)
文档属性
| 名称 | 2021-2022学年八年级数学人教版上册11.2与三角形有关的角优生辅导训练(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 665.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 20:55:18 | ||
图片预览


文档简介
2021-2022学年人教版八年级数学上册《11.2与三角形有关的角》优生辅导训练(附答案)
1.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32°
B.64°
C.77°
D.87°
2.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=
.(用α,β表示)
3.如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为
;第n个三角形中以An为顶点的底角的度数为
.
4.如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.其中正确的是
.
5.已知:如图,点D、E、F、G都在△ABC的边上,DE∥AC,且∠1+∠2=180°
(1)求证:AD∥FG;
(2)若DE平分∠ADB,∠C=40°,求∠BFG的度数.
6.如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
7.如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.
求证:∠DAE=(∠ABC﹣∠C).
8.如图,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠CFE=∠G.
(1)求证:AD∥EG;
(2)设∠B=x,∠G=y,若x﹣y=30°,∠ADC=110°,求∠B的度数.
9.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
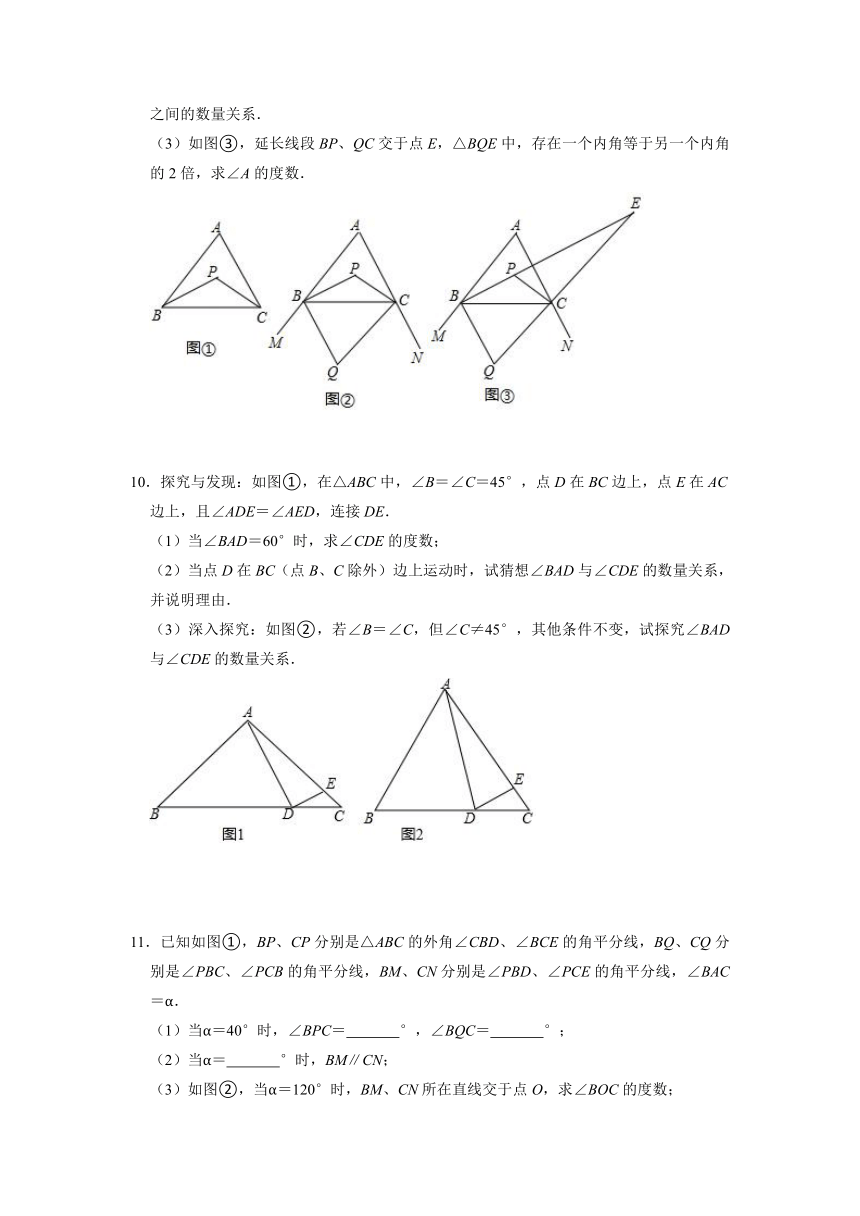
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
10.探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连接DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试猜想∠BAD与∠CDE的数量关系,并说明理由.
(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试探究∠BAD与∠CDE的数量关系.
11.已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC=
°,∠BQC=
°;
(2)当α=
°时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
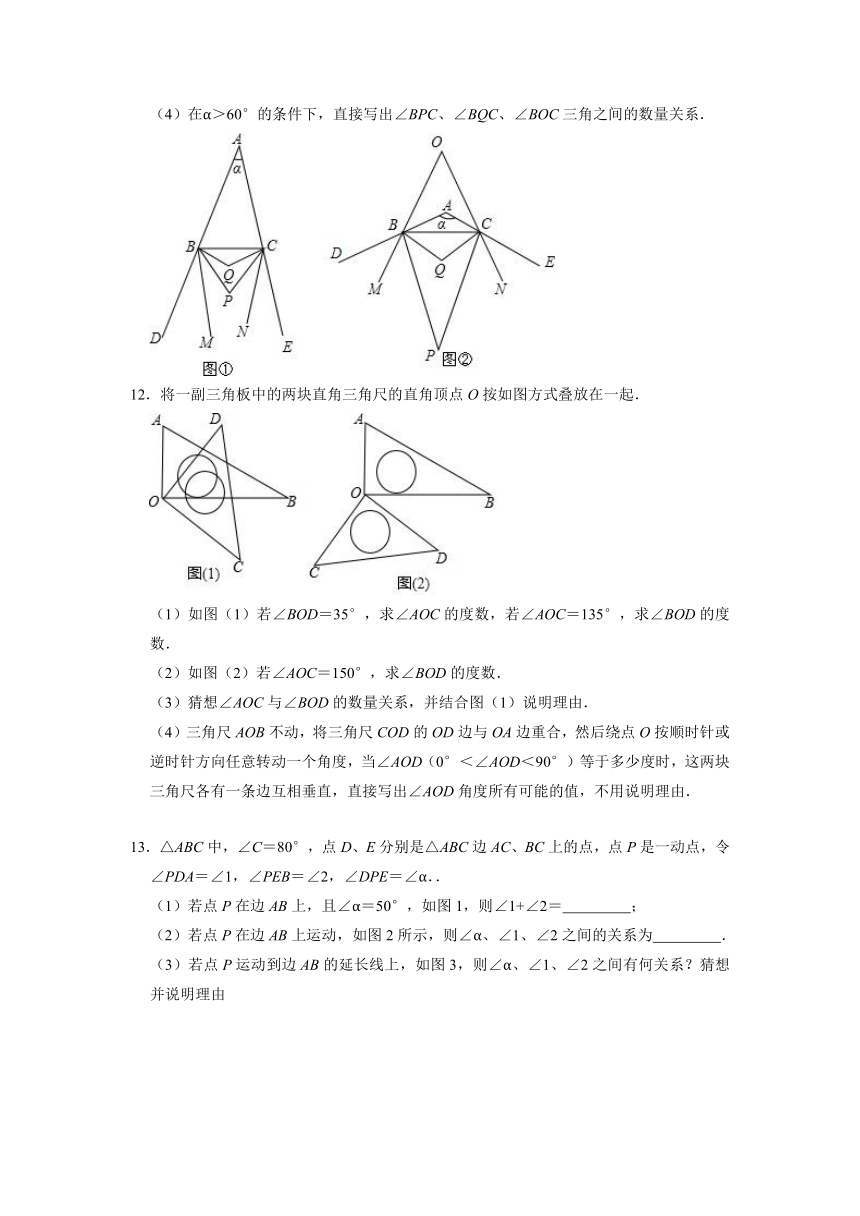
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系.
12.将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数.
(2)如图(2)若∠AOC=150°,求∠BOD的度数.
(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
13.△ABC中,∠C=80°,点D、E分别是△ABC边AC、BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α..
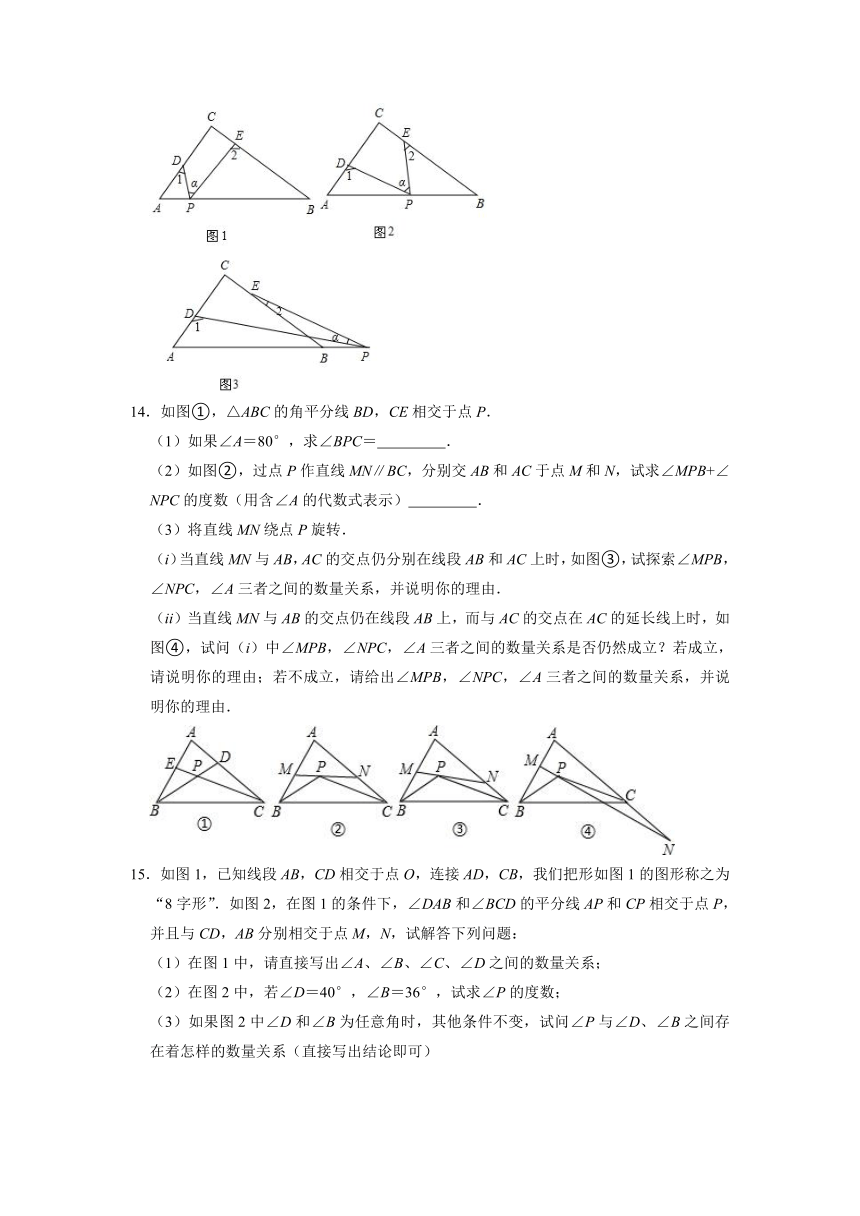
(1)若点P在边AB上,且∠α=50°,如图1,则∠1+∠2=
;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间的关系为
.
(3)若点P运动到边AB的延长线上,如图3,则∠α、∠1、∠2之间有何关系?猜想并说明理由
14.如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80°,求∠BPC=
.
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示)
.
(3)将直线MN绕点P旋转.
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由.
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由.
15.如图1,已知线段AB,CD相交于点O,连接AD,CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD,AB分别相交于点M,N,试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系(直接写出结论即可)
16.如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=82°,则∠BEC=
;若∠A=a°,则∠BEC=
.
【探究】
(1)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB,若∠A=a°,则∠BEC=
;
(2)如图3,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图4,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?请说明理由.
17.(1)如图①,已知任意△ABC,过点C作DE∥AB,求证:△ABC的三个内角(即∠A,∠B,∠ACB)之和等于180°;
(2)如图②,求证:∠AGF=∠AEF+∠F;
(3)如图③,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F的度数.
18.已知△ABC,D为△ABC所在平面上一点,BP平分∠ABD,CP平分∠ACD.
(1)若D点是△ABC中BC边上一点,如图1所示,判断∠P、∠A之间存在怎样的等量关系?并证明你的结论.
(2)若D点是△ABC中AB边上一点,如图2所示,判断∠BDC、∠BPC、∠A之间存在怎样的等量关系?并证明你的结论.
(3)若D点是△ABC外任一点,如图3所示,判断∠D、∠P、∠A之间存在怎样的等量关系?并证明你的结论.
(4)若D点是△ABC内一点,如图4所示,判断∠D、∠P、∠A之间存在怎样的等量关系?(直接写出结论,不需要证明)
19.△ABC中,三个内角的平分线交于点O,过点O作OD⊥OB,交边BC于点D.
(1)如图1,猜想∠AOC与∠ODC的关系,并说明你的理由;
(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.
①求证:BF∥OD;
②若∠F=35°,求∠BAC的度数.
20.(1)如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置.试写出∠A与∠1+∠2之间的关系,并说明理由;
(2)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED外部点A′的位置,如图②所示.此时∠A与∠1、∠2之间存在什么样的关系?直接写出
.
(3)如果把四边形ABCD沿EF折叠,使点A、D分别落在四边形BCFE内部点A′、D′的位置,如图③所示.直接写出∠A′、∠D′、∠1与∠2之间的关系
.
22.如图1,将纸片△ABC沿DE折叠,使点A落在A′处的位置.
(1)如果点A′落在四边形BCDE内部(如图1),∠A′、∠1、∠2之间有怎样的数量关系?并说明理由.
(2)如果点A′落在四边形BCDE的边BE上,则∠A′与∠2之间的数量关系是
.
(3)如果点A′落在四边形BCDE外部(如图2),∠A′、∠1、∠2之间有怎样的数量关系?并说明理由.
23.如图(1),在△OBC中,点A是BO延长线上的一点.
(1)∠B=32°,∠C=46°,则∠AOC=
°,Q是BC边上一点,连接AQ交OC边于点P,如图(2),若∠A=18°,则∠OPQ=
°,猜测:∠A+∠B+∠C与∠OPQ的大小关系是
;
(2)将图(2)中的CO延长到点D,AQ延长到点E,连接DE,得到图(3),则∠AQB等于图中哪三个角的和?并说明理由;
(3)求图(3)中∠A+∠D+∠B+∠E+∠C的度数.
24.如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化
说明你的结论的正确性.
(3)把图(2)中的点C向上移到BD上时(1)如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化说明你的结论的正确性.
25.如图,∠O=30°,任意裁剪的直角三角形纸板两条直角边所在直线与∠O的两边分别交于D、E两点.
(1)如图1,若直角顶点C在∠O的边上,则∠ADO+∠OEB=
度;
(2)如图2,若直角顶点C在∠O内部,求出∠ADO+∠OEB的度数;
(3)如图3,如果直角顶点C在∠O外部,求出∠ADO+∠OEB的度数.
参考答案
1.解:如图,取CF的中点T,连接DT,AT.
∵∠BAC=90°,FD⊥BC,
∴∠CAF=∠CDF=90°,
∴AT=DT=CF,
∴TD=TC=TA,
∴∠TDA=∠TAD,∠TDC=∠TCD,
∵∠ADB=45°,
∴∠ADT+∠TDC=135°,
∴∠ATC=360°﹣2×135°=90°,
∴AT⊥CF,
∵CT=TF,
∴AC=AF,
∴∠AFC=45°,
∴∠BFD=45°﹣32°=13°,
∵∠BDF=90°,
∴∠B=90°﹣∠BFD=77°,
故选:C.
2.解:连接BC,
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=ABP,∠4=ACP,
∵∠1+∠2=180°﹣β,2(∠3+∠4)+(∠1+∠2)=180°﹣α,
∴∠3+∠4=(β﹣α),
∵∠BQC=180°﹣(∠1+∠2)﹣(∠3+∠4)=180°﹣(180°﹣β)﹣(β﹣α),
即:∠BQC=(α+β).
故答案为:(α+β).
3.解:∵在△ABA1中,∠B=40°,AB=A1B,
∴∠BA1A=(180°﹣∠B)=(180°﹣40°)=70°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1=∠BA1A=×70°=35°;
同理可得,∠DA3A2=×70°=17.5°,∠EA4A3=×70°,
以此类推,第n个三角形的以An为顶点的底角的度数=.
故答案为:17.5°,.
4.解:①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
②正确;
③∠ABD=90°﹣∠BAC,
∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,
∵∠CBD=90°﹣∠C,
∴∠DBE=∠BAC﹣∠C﹣∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC﹣∠C﹣∠DBE,
∴∠F=(∠BAC﹣∠C);
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故答案为:①②③④.
5.证明:(1)∵DE∥AC
∴∠2=∠DAC
∵∠l+∠2=180°
∴∠1+∠DAC=180°
∴AD∥GF
(2)∵ED∥AC
∴∠EDB=∠C=40°
∵ED平分∠ADB
∴∠2=∠EDB=40°
∴∠ADB=80°
∵AD∥FG
∴∠BFG=∠ADB=80°
6.解(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°.
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°.
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°﹣∠ADE=15°;
(2)同(1),可得∠ADE=75°.
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°﹣∠ADE=15°.
7.证明:∵AD⊥BC,
∴∠D=90°,
∵∠ABC是△ABD的外角,
∴∠DAB=∠ABC﹣∠D=∠ABC﹣90°,
∵AE平分∠BAC,
∴∠BAE=∠BAC,
在△ABC中,∠BAC=180°﹣∠ABC﹣∠C,
∴∠BAE=90°﹣∠ABC﹣∠C,
∵∠DAE=∠DAB+∠BAE,
∴∠DAE=∠ABC﹣90°+90°﹣∠ABC﹣∠C=∠ABC﹣∠C,
即:∠DAE=(∠ABC﹣∠C).
8.解:(1)如图,
∵AD平分∠BAC,
∴∠1=∠2,
∵∠3=∠G,∠3=∠4,
∴∠4=∠G,
∵∠BAC=2∠3=∠G+∠4,
∴2∠2=∠4+∠4,
∴∠2=∠4,
∴AD∥EG;
(2)∵∠ADC=∠B+∠1=110°,
∴,
解得:,
∴∠B=70°
9.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
10.解:(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠BAD+∠B=105°,
∠DAE=∠BAC﹣∠BAD=30°,
∴∠ADE=∠AED=75°,
∴∠CDE=105°﹣75°=30°;
(2)∠BAD=2∠CDE,
理由如下:设∠BAD=x,
∴∠ADC=∠BAD+∠B=45°+x,
∠DAE=∠BAC﹣∠BAD=90°﹣x,
∴∠ADE=∠AED=,
∴∠CDE=45°+x﹣=x,
∴∠BAD=2∠CDE;
(3)设∠BAD=x,
∴∠ADC=∠BAD+∠B=∠B+x,
∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,
∴∠ADE=∠AED=∠C+x,
∴∠CDE=∠B+x﹣(∠C+x)=x,
∴∠BAD=2∠CDE.
11.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α,
∴(∠DBC+∠BCE)=180°,
即(180°+α)=180°,
解得α=60°;
(3)∵α=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°;
(4)∵α>60°,
∠BPC=90°﹣α、
∠BQC=135°﹣α、
∠BOC=α﹣45°.
∠BPC、∠BQC、∠BOC三角之间的数量关系:∠BPC+∠BQC+∠BOC=(90°﹣α)+(135°﹣α)+(α﹣45°)=180°.
故答案为:70,125;60;∠BPC+∠BQC+∠BOC=180°.
12.解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
(2)如图2,若∠AOC=150°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣150°﹣90°﹣90°
=30°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
13.解:(1)如图1,连接CP,
∵∠1是△CDP的外角,
∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+50°=130°,
故答案为:130°;
(2)如图,连接CP,
∵∠1是△CDP的外角,
∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+∠α,
故答案为:∠1+∠2=80°+∠α;
(3)∠1=80°+∠2+∠α,理由如下:
如图3,∵在△CDM中,∠1=∠C+∠CMD,
在△EMP中,∠CMD=∠2+∠α,
∴∠1=∠C+∠2+∠α,
即∠1=80°+∠2+∠α.
14.解:(1)∠BPC=180°﹣∠PBC﹣∠PCB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A
=90°+×80°
=130°;
故答案为:130°.
(2)∵∠BPC=90°+∠A,
∴∠MPB+∠NPC=180°﹣∠BPC=180°﹣(90°+∠A)=90°﹣∠A;
故答案为:∠MPB+∠NPC=90°﹣∠A.
(3)(i)∠MPB+∠NPC=90°﹣∠A.
理由如下:
∵∠BPC=90°+∠A,
∴∠MPB+∠NPC=180°﹣∠BPC=180°﹣(90°+∠A)=90°﹣∠A.
(ii)不成立,有∠MPB﹣∠NPC=90°﹣∠A.
理由如下:由题图④可知∠MPB+∠BPC﹣∠NPC=180°,
由(1)知:∠BPC=90°+∠A,
∴∠MPB﹣∠NPC=180°﹣∠BPC
=180°﹣(90°+∠A)
=90°﹣∠A.
15.解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB﹣∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D﹣∠PCM=(∠OAD﹣∠OCB)+∠D=×(﹣4°)+40°=38°;
(3)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
∴(∠D﹣∠B)=∠D﹣∠P,
整理得,2∠P=∠B+∠D.
16.解:∵∠A=82°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣82°=98°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=∠ABC,∠ECB=∠ACB,
∴∠EBC+∠ECB=(∠ABC+∠ACB)=×98°=49°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣49°=131°;
由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A=180°﹣a°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=∠ABC,∠ECB=∠ACB,
∴∠EBC+∠ECB=(∠ABC+∠ACB)=×(180°﹣a°)=90°﹣a°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(90°﹣a°)=90°+a°;
故答案为:131°,90°+a°;
探究:(1)由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A=180°﹣a°,
∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,
∴∠EBC=∠ABC,∠ECB=∠ACB,
∴∠EBC+∠ECB=(∠ABC+∠ACB)=×(180°﹣a°)=120°﹣a°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(120°﹣a°)=60°+a°;
故答案为:60°+a°;
(2)∠BOC=∠A.
理由如下:由三角形的外角性质得,∠ACD=∠A+∠ABC,
∠OCD=∠BOC+∠OBC,
∵O是∠ABC与外角∠ACD的平分线BO和CO的交点,
∴∠ABC=2∠OBC,∠ACD=2∠OCD,
∴∠A+∠ABC=2(∠BOC+∠OBC),
∴∠A=2∠BOC,
∴∠BOC=∠A;
(3)∠BOC=90°﹣∠A.
理由如下:∵O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,
∴∠OBC=(180°﹣∠ABC)=90°﹣∠ABC,∠OCB=(180°﹣∠ACB)=90°﹣∠ACB,
在△OBC中,∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(90°﹣∠ABC)﹣(90°﹣∠ACB)=(∠ABC+∠ACB),
由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=(180°﹣∠A)=90°﹣∠A.
17.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
故答案为:70°,125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,
∴(∠DBC+∠BCE)=180°,
即(180°+∠BAC)=180°,
解得∠BAC=60°;
(3)∵∠BAC=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°.
18.证明:(1)如图①所示,
在△ABC中,∵DE∥AB,
∴∠B=∠1,∠A=∠2(内错角相等).
∵∠1+∠ACB+∠2=180°,
∴∠A+∠B+∠C=180°
即三角形的内角和为180°;
(2)∵∠AGF+∠FGE=180°,
由(1)知,∠GEF+∠EFG+∠FGE=180°,
∴∠AGF=∠AEF+∠F;
(3)∵AB∥CD,∠CDE=119°,
∴∠DEB=119°,∠AED=61°,
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=59.5°,
∴∠AEF=120.5°,
∵∠AGF=150°,
∵∠AGF=∠AEF+∠F,
∴∠F=150°﹣120.5°=29.5°.
19.解:(1)∠P=90°+∠A.
证明:∵BP平分∠ABD,CP平分∠ACD,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠P=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A.
(2)∠A+∠BDC=2∠DPC.
∵CP平分∠ACD,
∴∠ACP=∠DCP,
∵∠DPC是△ACP的外角,∠BDC是△ACD的外角,
∴∠ACP=∠DPC﹣∠A,
∠DCP=∠BDC﹣∠DPC,
∴∠DPC﹣∠A=∠BDC﹣∠DPC,
∴∠A+∠BDC=2∠DPC;
(3)∠D+∠A=2∠P.
∵BP平分∠ABD,CP平分∠ACD,
∴∠DBP=∠ABP,∠ACP=∠DCP,
∵∠D+∠DBP=∠P+∠DCP,∠A+∠ACP=∠P+∠ABP,
∴两式相加,可得:∠D+∠A=2∠P;
(4)2∠BPC=∠BAC+∠BDC.
解法一:如图4,作射线PD,射线AP,
∵∠BDE是△BDP的外角,∠CDE是△CDP的外角,
∴∠BDC=∠PBD+∠BPC+∠DCP,①
同理可得,∠BPC=∠ABP+∠BAC+∠ACP,②
又∵BP平分∠ABD,CP平分∠ACD,
∴∠PBD=∠ABP,∠PCD=∠ACP,
∴由②﹣①,可得
∠BPC﹣∠BDC=∠BAC﹣∠BPC,
∴2∠BPC=∠BAC+∠BDC.
解法二:∵BP平分∠ABD,CP平分∠ACD,
∴∠PBD=∠ABP,∠PCD=∠ACP,
四边形BPDC中,∠P+∠ABD+∠ACD+360°﹣∠D=360°,
∴∠ABD+∠ACD=∠D﹣∠P,
在四边形ABPC中,∠A+∠ABD+∠ACD+360°﹣∠P=360°,
∴∠A+∠D﹣∠P﹣∠P=0,
∴2∠P=∠D+∠A.
20.解:(1)∠AOC=∠ODC,
理由:∵三个内角的平分线交于点O,
∴∠OAC+∠OCA=(∠BAC+∠BCA)=(180°﹣∠ABC),
∵∠OBC=∠ABC,
∴∠AOC=180°﹣(∠OAC+∠OCA)=90°+∠ABC=90°+∠OBC,
∵OD⊥OB,
∴∠BOD=90°,
∴∠ODC=90°+∠OBD,
∴∠AOC=∠ODC;
(2)①∵BF平分∠ABE,
∴∠EBF=∠ABE=(180°﹣∠ABC)=90°﹣∠DBO,
∵∠ODB=90°﹣∠OBD,
∴∠FBE=∠ODB,
∴BF∥OD;
②∵BF平分∠ABE,
∴∠FBE=∠ABE=(∠BAC+∠ACB),
∵三个内角的平分线交于点O,
∴∠FCB=∠ACB,
∵∠F=∠FBE﹣∠BCF=(∠BAC+∠ACB)﹣∠ACB=∠BAC,
∵∠F=35°,
∴∠BAC=2∠F=70°.
21.解:(1)如图,根据翻折的性质,∠3=(180﹣∠1),∠4=(180﹣∠2),
∵∠A+∠3+∠4=180°,
∴∠A+(180﹣∠1)+(180﹣∠2)=180°,
整理得,2∠A=∠1+∠2;
(2)根据翻折的性质,∠3=(180﹣∠1),∠4=(180+∠2),
∵∠A+∠3+∠4=180°,
∴∠A+(180﹣∠1)+(180+∠2)=180°,
整理得,2∠A=∠1﹣∠2;
(3)根据翻折的性质,∠3=(180﹣∠1),∠4=(180﹣∠2),
∵∠A+∠D+∠3+∠4=360°,
∴∠A+∠D+(180﹣∠1)+(180﹣∠2)=360°,
整理得,2(∠A+∠D)=∠1+∠2+360°,
即2(∠A'+∠D')=∠1+∠2+360°.
22.解:(1)2∠A=∠1+∠2,
理由:∵延DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°﹣∠A,
∠1+∠2=180°+180°﹣2(∠AED+∠ADE),
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;
(2)2∠A=∠2,如图3,
∠2=∠A+∠EA′D=2∠A,
故答案为:2∠A=∠2;
(3)2∠A=∠2﹣∠1,
理由:∵延DE折叠A和A′重合,
∴∠A=∠A′,
∵∠DME=∠A′+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A′+∠1,
即2∠A=∠2﹣∠1.
23.解:(1)∵∠B=32°,∠C=46°,
∴∠AOC=∠B+∠C=32°+46°=78°,
∵∠A=18°,
∴∠OPQ=∠A+∠AOC=18°+78°=96°,
∵∠A+∠B+∠C=18°+32°+46°=96°,
∴∠A+∠B+∠C=∠OPQ;
故答案为:78;96;∠A+∠B+∠C=∠OPQ;
(2)∠AQB=∠C+∠D+∠E,理由是:
∵∠EPC=∠D+∠E,∠AQB=∠C+∠EPC,
∴∠AQB=∠C+∠D+∠E;
(3)∵∠AQC=∠A+∠B,∠QPC=∠D+∠E,
又∵∠AQC+∠QPC+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
即∠A+∠D+∠B+∠E+∠C=180°.
24.解:(1)如图,连接CD.
在△ACD中,根据三角形内角和定理,得出∠A+∠2+∠3+∠ACE+∠ADB=180°.
∵∠1=∠B+∠E=∠2+∠3,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°;
(2)无变化.
根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.
∵∠BAC=∠C+∠E,∠EAD=∠B+∠D,
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°;
(3)无变化.
∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.
25.解:(1)∵∠ADB=90°,
∴∠ADO=90°﹣∠ODE,
∵∠OEB=∠O+∠ODE=30°+∠ODE,
∴∠ADO+∠OEB=90°﹣∠ODE+30°+∠ODE=120°.
故答案为:120°;
(2)如图2,连接OC,
∵∠ADO=∠ACO+∠DOC,∠OEB=∠EOC+∠ECO,
∠ACE=90°,∠DOE=30°,
∴∠ADO+∠OEB=∠ACO+∠DOC+∠EOC+∠ECO,
=(∠ACO+∠ECO)+(∠EOC+∠DOC)
=∠ACE+∠DOE
=90°+30°=120°;
(3)如图3,连接OC,
∵∠ADO=∠ACO﹣∠DOC,∠OEB=∠EOC+∠ECO,
∠ACE=90°,∠DOE=30°,
∴∠ADO+∠OEB=∠ACO﹣∠DOC+∠EOC+∠ECO
=(∠ACO+∠ECO)+(∠EOC﹣∠DOC)
=∠ACE+∠DOE
=90°+30°
=120°.
1.如图,在Rt△ABC中,∠BAC=90°,点D在BC上,过D作DF⊥BC交BA的延长线于F,连接AD,CF,若∠CFE=32°,∠ADB=45°,则∠B的大小是( )
A.32°
B.64°
C.77°
D.87°
2.已知如图,BQ平分∠ABP,CQ平分∠ACP,∠BAC=α,∠BPC=β,则∠BQC=
.(用α,β表示)
3.如图,在第1个△ABA1中,∠B=40°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第3个三角形中以A3为顶点的内角的度数为
;第n个三角形中以An为顶点的底角的度数为
.
4.如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.其中正确的是
.
5.已知:如图,点D、E、F、G都在△ABC的边上,DE∥AC,且∠1+∠2=180°
(1)求证:AD∥FG;
(2)若DE平分∠ADB,∠C=40°,求∠BFG的度数.
6.如图①,在△ABC中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.
7.如图,在△ABC中,AD⊥BC,垂足为D,AE平分∠BAC,且∠ABC>∠C.
求证:∠DAE=(∠ABC﹣∠C).
8.如图,△ABC中,AD平分∠BAC,EF交BA延长线于点G,∠CFE=∠G.
(1)求证:AD∥EG;
(2)设∠B=x,∠G=y,若x﹣y=30°,∠ADC=110°,求∠B的度数.
9.如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.
10.探究与发现:如图①,在△ABC中,∠B=∠C=45°,点D在BC边上,点E在AC边上,且∠ADE=∠AED,连接DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC(点B、C除外)边上运动时,试猜想∠BAD与∠CDE的数量关系,并说明理由.
(3)深入探究:如图②,若∠B=∠C,但∠C≠45°,其他条件不变,试探究∠BAD与∠CDE的数量关系.
11.已知如图①,BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,BQ、CQ分别是∠PBC、∠PCB的角平分线,BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α.
(1)当α=40°时,∠BPC=
°,∠BQC=
°;
(2)当α=
°时,BM∥CN;
(3)如图②,当α=120°时,BM、CN所在直线交于点O,求∠BOC的度数;
(4)在α>60°的条件下,直接写出∠BPC、∠BQC、∠BOC三角之间的数量关系.
12.将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数.
(2)如图(2)若∠AOC=150°,求∠BOD的度数.
(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
13.△ABC中,∠C=80°,点D、E分别是△ABC边AC、BC上的点,点P是一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α..
(1)若点P在边AB上,且∠α=50°,如图1,则∠1+∠2=
;
(2)若点P在边AB上运动,如图2所示,则∠α、∠1、∠2之间的关系为
.
(3)若点P运动到边AB的延长线上,如图3,则∠α、∠1、∠2之间有何关系?猜想并说明理由
14.如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80°,求∠BPC=
.
(2)如图②,过点P作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示)
.
(3)将直线MN绕点P旋转.
(i)当直线MN与AB,AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由.
(ii)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(i)中∠MPB,∠NPC,∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB,∠NPC,∠A三者之间的数量关系,并说明你的理由.
15.如图1,已知线段AB,CD相交于点O,连接AD,CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD,AB分别相交于点M,N,试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(3)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系(直接写出结论即可)
16.如图1,在△ABC中,BE平分∠ABC,CE平分∠ACB,若∠A=82°,则∠BEC=
;若∠A=a°,则∠BEC=
.
【探究】
(1)如图2,在△ABC中,BD,BE三等分∠ABC,CD,CE三等分∠ACB,若∠A=a°,则∠BEC=
;
(2)如图3,O是∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC和∠A有怎样的关系?请说明理由;
(3)如图4,O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?请说明理由.
17.(1)如图①,已知任意△ABC,过点C作DE∥AB,求证:△ABC的三个内角(即∠A,∠B,∠ACB)之和等于180°;
(2)如图②,求证:∠AGF=∠AEF+∠F;
(3)如图③,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=150°,求∠F的度数.
18.已知△ABC,D为△ABC所在平面上一点,BP平分∠ABD,CP平分∠ACD.
(1)若D点是△ABC中BC边上一点,如图1所示,判断∠P、∠A之间存在怎样的等量关系?并证明你的结论.
(2)若D点是△ABC中AB边上一点,如图2所示,判断∠BDC、∠BPC、∠A之间存在怎样的等量关系?并证明你的结论.
(3)若D点是△ABC外任一点,如图3所示,判断∠D、∠P、∠A之间存在怎样的等量关系?并证明你的结论.
(4)若D点是△ABC内一点,如图4所示,判断∠D、∠P、∠A之间存在怎样的等量关系?(直接写出结论,不需要证明)
19.△ABC中,三个内角的平分线交于点O,过点O作OD⊥OB,交边BC于点D.
(1)如图1,猜想∠AOC与∠ODC的关系,并说明你的理由;
(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.
①求证:BF∥OD;
②若∠F=35°,求∠BAC的度数.
20.(1)如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置.试写出∠A与∠1+∠2之间的关系,并说明理由;
(2)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED外部点A′的位置,如图②所示.此时∠A与∠1、∠2之间存在什么样的关系?直接写出
.
(3)如果把四边形ABCD沿EF折叠,使点A、D分别落在四边形BCFE内部点A′、D′的位置,如图③所示.直接写出∠A′、∠D′、∠1与∠2之间的关系
.
22.如图1,将纸片△ABC沿DE折叠,使点A落在A′处的位置.
(1)如果点A′落在四边形BCDE内部(如图1),∠A′、∠1、∠2之间有怎样的数量关系?并说明理由.
(2)如果点A′落在四边形BCDE的边BE上,则∠A′与∠2之间的数量关系是
.
(3)如果点A′落在四边形BCDE外部(如图2),∠A′、∠1、∠2之间有怎样的数量关系?并说明理由.
23.如图(1),在△OBC中,点A是BO延长线上的一点.
(1)∠B=32°,∠C=46°,则∠AOC=
°,Q是BC边上一点,连接AQ交OC边于点P,如图(2),若∠A=18°,则∠OPQ=
°,猜测:∠A+∠B+∠C与∠OPQ的大小关系是
;
(2)将图(2)中的CO延长到点D,AQ延长到点E,连接DE,得到图(3),则∠AQB等于图中哪三个角的和?并说明理由;
(3)求图(3)中∠A+∠D+∠B+∠E+∠C的度数.
24.如下几个图形是五角星和它的变形.
(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.
(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化
说明你的结论的正确性.
(3)把图(2)中的点C向上移到BD上时(1)如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化说明你的结论的正确性.
25.如图,∠O=30°,任意裁剪的直角三角形纸板两条直角边所在直线与∠O的两边分别交于D、E两点.
(1)如图1,若直角顶点C在∠O的边上,则∠ADO+∠OEB=
度;
(2)如图2,若直角顶点C在∠O内部,求出∠ADO+∠OEB的度数;
(3)如图3,如果直角顶点C在∠O外部,求出∠ADO+∠OEB的度数.
参考答案
1.解:如图,取CF的中点T,连接DT,AT.
∵∠BAC=90°,FD⊥BC,
∴∠CAF=∠CDF=90°,
∴AT=DT=CF,
∴TD=TC=TA,
∴∠TDA=∠TAD,∠TDC=∠TCD,
∵∠ADB=45°,
∴∠ADT+∠TDC=135°,
∴∠ATC=360°﹣2×135°=90°,
∴AT⊥CF,
∵CT=TF,
∴AC=AF,
∴∠AFC=45°,
∴∠BFD=45°﹣32°=13°,
∵∠BDF=90°,
∴∠B=90°﹣∠BFD=77°,
故选:C.
2.解:连接BC,
∵BQ平分∠ABP,CQ平分∠ACP,
∴∠3=ABP,∠4=ACP,
∵∠1+∠2=180°﹣β,2(∠3+∠4)+(∠1+∠2)=180°﹣α,
∴∠3+∠4=(β﹣α),
∵∠BQC=180°﹣(∠1+∠2)﹣(∠3+∠4)=180°﹣(180°﹣β)﹣(β﹣α),
即:∠BQC=(α+β).
故答案为:(α+β).
3.解:∵在△ABA1中,∠B=40°,AB=A1B,
∴∠BA1A=(180°﹣∠B)=(180°﹣40°)=70°,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1=∠BA1A=×70°=35°;
同理可得,∠DA3A2=×70°=17.5°,∠EA4A3=×70°,
以此类推,第n个三角形的以An为顶点的底角的度数=.
故答案为:17.5°,.
4.解:①∵BD⊥FD,
∴∠FGD+∠F=90°,
∵FH⊥BE,
∴∠BGH+∠DBE=90°,
∵∠FGD=∠BGH,
∴∠DBE=∠F,
①正确;
②∵BE平分∠ABC,
∴∠ABE=∠CBE,
∠BEF=∠CBE+∠C,
∴2∠BEF=∠ABC+2∠C,
∠BAF=∠ABC+∠C,
∴2∠BEF=∠BAF+∠C,
②正确;
③∠ABD=90°﹣∠BAC,
∠DBE=∠ABE﹣∠ABD=∠ABE﹣90°+∠BAC=∠CBD﹣∠DBE﹣90°+∠BAC,
∵∠CBD=90°﹣∠C,
∴∠DBE=∠BAC﹣∠C﹣∠DBE,
由①得,∠DBE=∠F,
∴∠F=∠BAC﹣∠C﹣∠DBE,
∴∠F=(∠BAC﹣∠C);
③正确;
④∵∠AEB=∠EBC+∠C,
∵∠ABE=∠CBE,
∴∠AEB=∠ABE+∠C,
∵BD⊥FC,FH⊥BE,
∴∠FGD=∠FEB,
∴∠BGH=∠ABE+∠C,
④正确,
故答案为:①②③④.
5.证明:(1)∵DE∥AC
∴∠2=∠DAC
∵∠l+∠2=180°
∴∠1+∠DAC=180°
∴AD∥GF
(2)∵ED∥AC
∴∠EDB=∠C=40°
∵ED平分∠ADB
∴∠2=∠EDB=40°
∴∠ADB=80°
∵AD∥FG
∴∠BFG=∠ADB=80°
6.解(1)∵∠B=40°,∠C=70°,
∴∠BAC=70°.
∵AD平分∠BAC,
∴∠BAD=∠CAD=35°,
∴∠ADE=∠B+∠BAD=75°.
∵AE⊥BC,
∴∠AEB=90°,
∴∠DAE=90°﹣∠ADE=15°;
(2)同(1),可得∠ADE=75°.
∵FE⊥BC,
∴∠FEB=90°,
∴∠DFE=90°﹣∠ADE=15°.
7.证明:∵AD⊥BC,
∴∠D=90°,
∵∠ABC是△ABD的外角,
∴∠DAB=∠ABC﹣∠D=∠ABC﹣90°,
∵AE平分∠BAC,
∴∠BAE=∠BAC,
在△ABC中,∠BAC=180°﹣∠ABC﹣∠C,
∴∠BAE=90°﹣∠ABC﹣∠C,
∵∠DAE=∠DAB+∠BAE,
∴∠DAE=∠ABC﹣90°+90°﹣∠ABC﹣∠C=∠ABC﹣∠C,
即:∠DAE=(∠ABC﹣∠C).
8.解:(1)如图,
∵AD平分∠BAC,
∴∠1=∠2,
∵∠3=∠G,∠3=∠4,
∴∠4=∠G,
∵∠BAC=2∠3=∠G+∠4,
∴2∠2=∠4+∠4,
∴∠2=∠4,
∴AD∥EG;
(2)∵∠ADC=∠B+∠1=110°,
∴,
解得:,
∴∠B=70°
9.(1)解:∵∠A=80°.
∴∠ABC+∠ACB=100°,
∵点P是∠ABC和∠ACB的平分线的交点,
∴∠P=180°﹣(∠ABC+∠ACB)=180°﹣×100°=130°,
(2)∵外角∠MBC,∠NCB的角平分线交于点Q,
∴∠QBC+∠QCB=(∠MBC+∠NCB)
=(360°﹣∠ABC﹣∠ACB)
=(180°+∠A)
=90°+∠A
∴∠Q=180°﹣(90°+∠A)=90°﹣∠A;
(3)延长BC至F,
∵CQ为△ABC的外角∠NCB的角平分线,
∴CE是△ABC的外角∠ACF的平分线,
∴∠ACF=2∠ECF,
∵BE平分∠ABC,
∴∠ABC=2∠EBC,
∵∠ECF=∠EBC+∠E,
∴2∠ECF=2∠EBC+2∠E,
即∠ACF=∠ABC+2∠E,
又∵∠ACF=∠ABC+∠A,
∴∠A=2∠E,即∠E=∠A;
∵∠EBQ=∠EBC+∠CBQ
=∠ABC+∠MBC
=(∠ABC+∠A+∠ACB)=90°.
如果△BQE中,存在一个内角等于另一个内角的2倍,那么分四种情况:
①∠EBQ=2∠E=90°,则∠E=45°,∠A=2∠E=90°;
②∠EBQ=2∠Q=90°,则∠Q=45°,∠E=45°,∠A=2∠E=90°;
③∠Q=2∠E,则90°﹣∠A=∠A,解得∠A=60°;
④∠E=2∠Q,则∠A=2(90°﹣∠A),解得∠A=120°.
综上所述,∠A的度数是90°或60°或120°.
10.解:(1)∵∠ADC是△ABD的外角,
∴∠ADC=∠BAD+∠B=105°,
∠DAE=∠BAC﹣∠BAD=30°,
∴∠ADE=∠AED=75°,
∴∠CDE=105°﹣75°=30°;
(2)∠BAD=2∠CDE,
理由如下:设∠BAD=x,
∴∠ADC=∠BAD+∠B=45°+x,
∠DAE=∠BAC﹣∠BAD=90°﹣x,
∴∠ADE=∠AED=,
∴∠CDE=45°+x﹣=x,
∴∠BAD=2∠CDE;
(3)设∠BAD=x,
∴∠ADC=∠BAD+∠B=∠B+x,
∠DAE=∠BAC﹣∠BAD=180°﹣2∠C﹣x,
∴∠ADE=∠AED=∠C+x,
∴∠CDE=∠B+x﹣(∠C+x)=x,
∴∠BAD=2∠CDE.
11.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,∠BAC=α,
∴(∠DBC+∠BCE)=180°,
即(180°+α)=180°,
解得α=60°;
(3)∵α=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°;
(4)∵α>60°,
∠BPC=90°﹣α、
∠BQC=135°﹣α、
∠BOC=α﹣45°.
∠BPC、∠BQC、∠BOC三角之间的数量关系:∠BPC+∠BQC+∠BOC=(90°﹣α)+(135°﹣α)+(α﹣45°)=180°.
故答案为:70,125;60;∠BPC+∠BQC+∠BOC=180°.
12.解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
(2)如图2,若∠AOC=150°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣150°﹣90°﹣90°
=30°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
13.解:(1)如图1,连接CP,
∵∠1是△CDP的外角,
∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+50°=130°,
故答案为:130°;
(2)如图,连接CP,
∵∠1是△CDP的外角,
∴∠1=∠DCP+∠DPC,
同理可得,∠2=∠ECP+∠EPC,
∴∠1+∠2=∠ACB+∠DPE=80°+∠α,
故答案为:∠1+∠2=80°+∠α;
(3)∠1=80°+∠2+∠α,理由如下:
如图3,∵在△CDM中,∠1=∠C+∠CMD,
在△EMP中,∠CMD=∠2+∠α,
∴∠1=∠C+∠2+∠α,
即∠1=80°+∠2+∠α.
14.解:(1)∠BPC=180°﹣∠PBC﹣∠PCB
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠A)
=90°+∠A
=90°+×80°
=130°;
故答案为:130°.
(2)∵∠BPC=90°+∠A,
∴∠MPB+∠NPC=180°﹣∠BPC=180°﹣(90°+∠A)=90°﹣∠A;
故答案为:∠MPB+∠NPC=90°﹣∠A.
(3)(i)∠MPB+∠NPC=90°﹣∠A.
理由如下:
∵∠BPC=90°+∠A,
∴∠MPB+∠NPC=180°﹣∠BPC=180°﹣(90°+∠A)=90°﹣∠A.
(ii)不成立,有∠MPB﹣∠NPC=90°﹣∠A.
理由如下:由题图④可知∠MPB+∠BPC﹣∠NPC=180°,
由(1)知:∠BPC=90°+∠A,
∴∠MPB﹣∠NPC=180°﹣∠BPC
=180°﹣(90°+∠A)
=90°﹣∠A.
15.解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB﹣∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D﹣∠PCM=(∠OAD﹣∠OCB)+∠D=×(﹣4°)+40°=38°;
(3)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
∴(∠D﹣∠B)=∠D﹣∠P,
整理得,2∠P=∠B+∠D.
16.解:∵∠A=82°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣82°=98°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=∠ABC,∠ECB=∠ACB,
∴∠EBC+∠ECB=(∠ABC+∠ACB)=×98°=49°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣49°=131°;
由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A=180°﹣a°,
∵BE平分∠ABC,CE平分∠ACB,
∴∠EBC=∠ABC,∠ECB=∠ACB,
∴∠EBC+∠ECB=(∠ABC+∠ACB)=×(180°﹣a°)=90°﹣a°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(90°﹣a°)=90°+a°;
故答案为:131°,90°+a°;
探究:(1)由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A=180°﹣a°,
∵BD,BE三等分∠ABC,CD,CE三等分∠ACB,
∴∠EBC=∠ABC,∠ECB=∠ACB,
∴∠EBC+∠ECB=(∠ABC+∠ACB)=×(180°﹣a°)=120°﹣a°,
∴∠BEC=180°﹣(∠EBC+∠ECB)=180°﹣(120°﹣a°)=60°+a°;
故答案为:60°+a°;
(2)∠BOC=∠A.
理由如下:由三角形的外角性质得,∠ACD=∠A+∠ABC,
∠OCD=∠BOC+∠OBC,
∵O是∠ABC与外角∠ACD的平分线BO和CO的交点,
∴∠ABC=2∠OBC,∠ACD=2∠OCD,
∴∠A+∠ABC=2(∠BOC+∠OBC),
∴∠A=2∠BOC,
∴∠BOC=∠A;
(3)∠BOC=90°﹣∠A.
理由如下:∵O是外角∠DBC与外角∠BCE的平分线BO和CO的交点,
∴∠OBC=(180°﹣∠ABC)=90°﹣∠ABC,∠OCB=(180°﹣∠ACB)=90°﹣∠ACB,
在△OBC中,∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(90°﹣∠ABC)﹣(90°﹣∠ACB)=(∠ABC+∠ACB),
由三角形的内角和定理得,∠ABC+∠ACB=180°﹣∠A,
∴∠BOC=(180°﹣∠A)=90°﹣∠A.
17.解:(1)∵∠DBC=∠A+∠ACB,∠BCE=∠A+∠ABC,
∴∠DBC+∠BCE=180°+∠A=220°,
∵BP、CP分别是△ABC的外角∠CBD、∠BCE的角平分线,
∴∠CBP+∠BCP=(∠DBC+∠BCE)=110°,
∴∠BPC=180°﹣110°=70°,
∵BQ、CQ分别是∠PBC、∠PCB的角平分线,
∴∠QBC=∠PBC,∠QCB=∠PCB,
∴∠QBC+∠QCB=55°,
∴∠BQC=180°﹣55°=125°;
故答案为:70°,125°;
(2)∵BM∥CN,
∴∠MBC+∠NCB=180°,
∵BM、CN分别是∠PBD、∠PCE的角平分线,
∴(∠DBC+∠BCE)=180°,
即(180°+∠BAC)=180°,
解得∠BAC=60°;
(3)∵∠BAC=120°,
∴∠MBC+∠NCB=(∠DBC+∠BCE)=(180°+α)=225°,
∴∠BOC=225°﹣180°=45°.
18.证明:(1)如图①所示,
在△ABC中,∵DE∥AB,
∴∠B=∠1,∠A=∠2(内错角相等).
∵∠1+∠ACB+∠2=180°,
∴∠A+∠B+∠C=180°
即三角形的内角和为180°;
(2)∵∠AGF+∠FGE=180°,
由(1)知,∠GEF+∠EFG+∠FGE=180°,
∴∠AGF=∠AEF+∠F;
(3)∵AB∥CD,∠CDE=119°,
∴∠DEB=119°,∠AED=61°,
∵GF交∠DEB的平分线EF于点F,
∴∠DEF=59.5°,
∴∠AEF=120.5°,
∵∠AGF=150°,
∵∠AGF=∠AEF+∠F,
∴∠F=150°﹣120.5°=29.5°.
19.解:(1)∠P=90°+∠A.
证明:∵BP平分∠ABD,CP平分∠ACD,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠P=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)=180°﹣(180°﹣∠A)=90°+∠A.
(2)∠A+∠BDC=2∠DPC.
∵CP平分∠ACD,
∴∠ACP=∠DCP,
∵∠DPC是△ACP的外角,∠BDC是△ACD的外角,
∴∠ACP=∠DPC﹣∠A,
∠DCP=∠BDC﹣∠DPC,
∴∠DPC﹣∠A=∠BDC﹣∠DPC,
∴∠A+∠BDC=2∠DPC;
(3)∠D+∠A=2∠P.
∵BP平分∠ABD,CP平分∠ACD,
∴∠DBP=∠ABP,∠ACP=∠DCP,
∵∠D+∠DBP=∠P+∠DCP,∠A+∠ACP=∠P+∠ABP,
∴两式相加,可得:∠D+∠A=2∠P;
(4)2∠BPC=∠BAC+∠BDC.
解法一:如图4,作射线PD,射线AP,
∵∠BDE是△BDP的外角,∠CDE是△CDP的外角,
∴∠BDC=∠PBD+∠BPC+∠DCP,①
同理可得,∠BPC=∠ABP+∠BAC+∠ACP,②
又∵BP平分∠ABD,CP平分∠ACD,
∴∠PBD=∠ABP,∠PCD=∠ACP,
∴由②﹣①,可得
∠BPC﹣∠BDC=∠BAC﹣∠BPC,
∴2∠BPC=∠BAC+∠BDC.
解法二:∵BP平分∠ABD,CP平分∠ACD,
∴∠PBD=∠ABP,∠PCD=∠ACP,
四边形BPDC中,∠P+∠ABD+∠ACD+360°﹣∠D=360°,
∴∠ABD+∠ACD=∠D﹣∠P,
在四边形ABPC中,∠A+∠ABD+∠ACD+360°﹣∠P=360°,
∴∠A+∠D﹣∠P﹣∠P=0,
∴2∠P=∠D+∠A.
20.解:(1)∠AOC=∠ODC,
理由:∵三个内角的平分线交于点O,
∴∠OAC+∠OCA=(∠BAC+∠BCA)=(180°﹣∠ABC),
∵∠OBC=∠ABC,
∴∠AOC=180°﹣(∠OAC+∠OCA)=90°+∠ABC=90°+∠OBC,
∵OD⊥OB,
∴∠BOD=90°,
∴∠ODC=90°+∠OBD,
∴∠AOC=∠ODC;
(2)①∵BF平分∠ABE,
∴∠EBF=∠ABE=(180°﹣∠ABC)=90°﹣∠DBO,
∵∠ODB=90°﹣∠OBD,
∴∠FBE=∠ODB,
∴BF∥OD;
②∵BF平分∠ABE,
∴∠FBE=∠ABE=(∠BAC+∠ACB),
∵三个内角的平分线交于点O,
∴∠FCB=∠ACB,
∵∠F=∠FBE﹣∠BCF=(∠BAC+∠ACB)﹣∠ACB=∠BAC,
∵∠F=35°,
∴∠BAC=2∠F=70°.
21.解:(1)如图,根据翻折的性质,∠3=(180﹣∠1),∠4=(180﹣∠2),
∵∠A+∠3+∠4=180°,
∴∠A+(180﹣∠1)+(180﹣∠2)=180°,
整理得,2∠A=∠1+∠2;
(2)根据翻折的性质,∠3=(180﹣∠1),∠4=(180+∠2),
∵∠A+∠3+∠4=180°,
∴∠A+(180﹣∠1)+(180+∠2)=180°,
整理得,2∠A=∠1﹣∠2;
(3)根据翻折的性质,∠3=(180﹣∠1),∠4=(180﹣∠2),
∵∠A+∠D+∠3+∠4=360°,
∴∠A+∠D+(180﹣∠1)+(180﹣∠2)=360°,
整理得,2(∠A+∠D)=∠1+∠2+360°,
即2(∠A'+∠D')=∠1+∠2+360°.
22.解:(1)2∠A=∠1+∠2,
理由:∵延DE折叠A和A′重合,
∴∠AED=∠A′ED,∠ADE=∠A′DE,
∵∠AED+∠ADE=180°﹣∠A,
∠1+∠2=180°+180°﹣2(∠AED+∠ADE),
∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;
(2)2∠A=∠2,如图3,
∠2=∠A+∠EA′D=2∠A,
故答案为:2∠A=∠2;
(3)2∠A=∠2﹣∠1,
理由:∵延DE折叠A和A′重合,
∴∠A=∠A′,
∵∠DME=∠A′+∠1,∠2=∠A+∠DME,
∴∠2=∠A+∠A′+∠1,
即2∠A=∠2﹣∠1.
23.解:(1)∵∠B=32°,∠C=46°,
∴∠AOC=∠B+∠C=32°+46°=78°,
∵∠A=18°,
∴∠OPQ=∠A+∠AOC=18°+78°=96°,
∵∠A+∠B+∠C=18°+32°+46°=96°,
∴∠A+∠B+∠C=∠OPQ;
故答案为:78;96;∠A+∠B+∠C=∠OPQ;
(2)∠AQB=∠C+∠D+∠E,理由是:
∵∠EPC=∠D+∠E,∠AQB=∠C+∠EPC,
∴∠AQB=∠C+∠D+∠E;
(3)∵∠AQC=∠A+∠B,∠QPC=∠D+∠E,
又∵∠AQC+∠QPC+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
即∠A+∠D+∠B+∠E+∠C=180°.
24.解:(1)如图,连接CD.
在△ACD中,根据三角形内角和定理,得出∠A+∠2+∠3+∠ACE+∠ADB=180°.
∵∠1=∠B+∠E=∠2+∠3,
∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°;
(2)无变化.
根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.
∵∠BAC=∠C+∠E,∠EAD=∠B+∠D,
∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°;
(3)无变化.
∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,
∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.
25.解:(1)∵∠ADB=90°,
∴∠ADO=90°﹣∠ODE,
∵∠OEB=∠O+∠ODE=30°+∠ODE,
∴∠ADO+∠OEB=90°﹣∠ODE+30°+∠ODE=120°.
故答案为:120°;
(2)如图2,连接OC,
∵∠ADO=∠ACO+∠DOC,∠OEB=∠EOC+∠ECO,
∠ACE=90°,∠DOE=30°,
∴∠ADO+∠OEB=∠ACO+∠DOC+∠EOC+∠ECO,
=(∠ACO+∠ECO)+(∠EOC+∠DOC)
=∠ACE+∠DOE
=90°+30°=120°;
(3)如图3,连接OC,
∵∠ADO=∠ACO﹣∠DOC,∠OEB=∠EOC+∠ECO,
∠ACE=90°,∠DOE=30°,
∴∠ADO+∠OEB=∠ACO﹣∠DOC+∠EOC+∠ECO
=(∠ACO+∠ECO)+(∠EOC﹣∠DOC)
=∠ACE+∠DOE
=90°+30°
=120°.
