2021-2022学年人教版数学九年级上册22.3实际问题与二次函数同步练习(word版、含答案)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册22.3实际问题与二次函数同步练习(word版、含答案) | 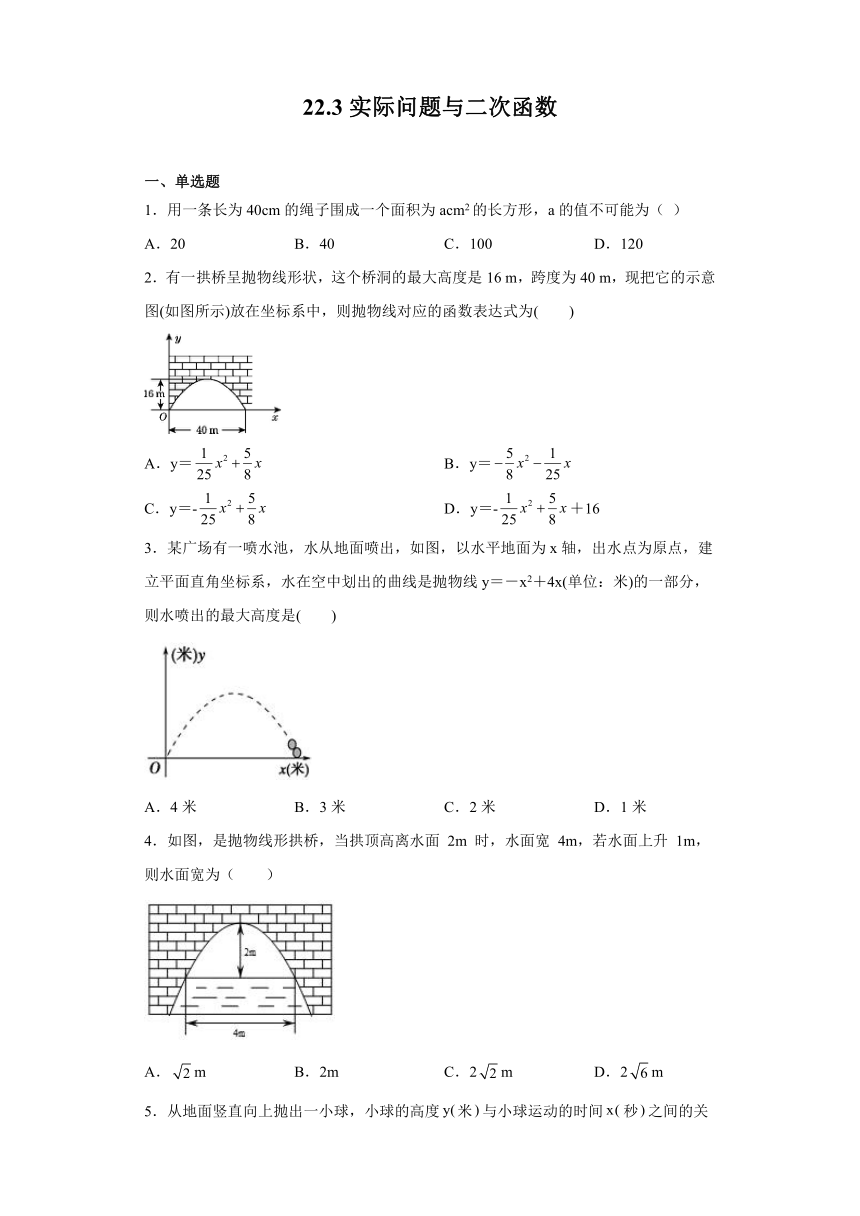 | |
| 格式 | docx | ||
| 文件大小 | 173.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-12 21:02:40 | ||
图片预览


文档简介
22.3实际问题与二次函数
一、单选题
1.用一条长为40cm的绳子围成一个面积为acm2的长方形,a的值不可能为(
)
A.20
B.40
C.100
D.120
2.有一拱桥呈抛物线形状,这个桥洞的最大高度是16
m,跨度为40
m,现把它的示意图(如图所示)放在坐标系中,则抛物线对应的函数表达式为( )
A.y=
B.y=
C.y=-
D.y=-+16
3.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
4.如图,是抛物线形拱桥,当拱顶高离水面
2m
时,水面宽
4m,若水面上升
1m,则水面宽为(
)
A.m
B.2m
C.2m
D.2m
5.从地面竖直向上抛出一小球,小球的高度米与小球运动的时间秒之间的关系式为若小球在第7秒与第14秒时的高度相同,则在下列时间中小球所在高度最高的是
A.第8秒
B.第10秒
C.第12秒
D.第15秒
6.某超市有一种商品,进价为2元,据市场调查,销售单价是13元时,平均每天销售量是50件,而销售价每降低1元,平均每天就可以多售出10件.若设降价后售价为x元,每天利润为y元,则y与x之间的函数关系为( )
A.y=10x2﹣100x﹣160?????????????????????????????????????????
B.y=﹣10x2+200x﹣360
C.y=x2﹣20x+36??????????????????????????????????????????????????
D.y=﹣10x2+310x﹣2340
7.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则与的关系式为(
)
A.
B.
C.
D.
8.某产品进货单价为元,按一件售出时,能售件,如果这种商品每涨价元,其销售量就减少件,设每件产品涨元,所获利润为元,可得函数关系式为(
)
A.
B.
C.
D.
9.某民俗旅游村为接待游客住宿需要,开设了有张床位的旅馆,当每张床位每天收费元时,床位可全部租出.若每张床位每天收费提高元,则相应的减少了张床位租出.如果每张床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是(
)
A.14元
B.15元
C.16元
D.18元
10.如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是(
)
A.B.C.D.
二、填空题
11.某工厂第一年的利润是20万元,第三年的利润是y万元,与平均年增长率x之间的函数关系式是______________.
12.某种商品每件进价为10元,调查表明:在某段时间内若以每件x元(10≤x≤20且x为整数)出售,可卖出(20﹣x)件,若使利润最大,则每件商品的售价应为_____元.
13.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数表达式为y=-x2+x+,那么铅球运动过程中最高点离地面的距离为________米.
14.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为_________米.
15.某商场购进一批单价为元的日用品,经试销发现,若按每件元的价格销售时,每月能卖件,若按每件元的价格销售时,每月能卖件,假定每月销售件数(件)是价格(元/件)的一次函数,则与之间的关系式是________,销售所获得的利润为(元)与价格(元/件)的关系式是________.
三、解答题
16.在美化校园的活动中,某兴趣小组用总长为米的围栏材料,一面靠墙,围成一个矩形花园,墙长米,设的长为米,矩形花园的面积为平方米,当为多少时,取得最大值,最大值是多少?
17.小明和小丽先后从A地出发同一直道去B地,
设小丽出发第时,
小丽、小明离B地的距离分别为、,与x之间的数表达式,与x之间的函数表达式是.
(1)小丽出发时,小明离A地的距离为
.
(2)小丽发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?
18.网络销售已经成为一种热门的销售方式为了减少农产品的库存,我市市长亲自在某网络平台上进行直播销售大别山牌板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元,每日销售量与销售单价x(元)满足关系式:.经销售发现,销售单价不低于成本价格且不高于30元.当每日销售量不低于时,每千克成本将降低1元设板栗公司销售该板栗的日获利为W(元).
(1)请求出日获利W与销售单价x之间的函数关系式
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当元时,网络平台将向板栗公可收取a元的相关费用,若此时日获利的最大值为42100元,求a的值.
参考答案
1.D
2.C
3.A
4.C
5.B
6.B
7.C
8.D
9.C
10.A
11.
12.15
13.2
14.0.5
15.
16.80
17.(1)250;(2)当小丽出发第时,两人相距最近,最近距离是
18.(1);(2)当销售单价定为28元时,日获利最大,且最大为46400元;(3)
一、单选题
1.用一条长为40cm的绳子围成一个面积为acm2的长方形,a的值不可能为(
)
A.20
B.40
C.100
D.120
2.有一拱桥呈抛物线形状,这个桥洞的最大高度是16
m,跨度为40
m,现把它的示意图(如图所示)放在坐标系中,则抛物线对应的函数表达式为( )
A.y=
B.y=
C.y=-
D.y=-+16
3.某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=-x2+4x(单位:米)的一部分,则水喷出的最大高度是( )
A.4米
B.3米
C.2米
D.1米
4.如图,是抛物线形拱桥,当拱顶高离水面
2m
时,水面宽
4m,若水面上升
1m,则水面宽为(
)
A.m
B.2m
C.2m
D.2m
5.从地面竖直向上抛出一小球,小球的高度米与小球运动的时间秒之间的关系式为若小球在第7秒与第14秒时的高度相同,则在下列时间中小球所在高度最高的是
A.第8秒
B.第10秒
C.第12秒
D.第15秒
6.某超市有一种商品,进价为2元,据市场调查,销售单价是13元时,平均每天销售量是50件,而销售价每降低1元,平均每天就可以多售出10件.若设降价后售价为x元,每天利润为y元,则y与x之间的函数关系为( )
A.y=10x2﹣100x﹣160?????????????????????????????????????????
B.y=﹣10x2+200x﹣360
C.y=x2﹣20x+36??????????????????????????????????????????????????
D.y=﹣10x2+310x﹣2340
7.长为,宽为的矩形,四个角上剪去边长为的小正方形,然后把四边折起来,作成底面为的无盖的长方体盒子,则与的关系式为(
)
A.
B.
C.
D.
8.某产品进货单价为元,按一件售出时,能售件,如果这种商品每涨价元,其销售量就减少件,设每件产品涨元,所获利润为元,可得函数关系式为(
)
A.
B.
C.
D.
9.某民俗旅游村为接待游客住宿需要,开设了有张床位的旅馆,当每张床位每天收费元时,床位可全部租出.若每张床位每天收费提高元,则相应的减少了张床位租出.如果每张床位每天以元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是(
)
A.14元
B.15元
C.16元
D.18元
10.如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是(
)
A.B.C.D.
二、填空题
11.某工厂第一年的利润是20万元,第三年的利润是y万元,与平均年增长率x之间的函数关系式是______________.
12.某种商品每件进价为10元,调查表明:在某段时间内若以每件x元(10≤x≤20且x为整数)出售,可卖出(20﹣x)件,若使利润最大,则每件商品的售价应为_____元.
13.如图,小李推铅球,如果铅球运行时离地面的高度y(米)关于水平距离x(米)的函数表达式为y=-x2+x+,那么铅球运动过程中最高点离地面的距离为________米.
14.如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为_________米.
15.某商场购进一批单价为元的日用品,经试销发现,若按每件元的价格销售时,每月能卖件,若按每件元的价格销售时,每月能卖件,假定每月销售件数(件)是价格(元/件)的一次函数,则与之间的关系式是________,销售所获得的利润为(元)与价格(元/件)的关系式是________.
三、解答题
16.在美化校园的活动中,某兴趣小组用总长为米的围栏材料,一面靠墙,围成一个矩形花园,墙长米,设的长为米,矩形花园的面积为平方米,当为多少时,取得最大值,最大值是多少?
17.小明和小丽先后从A地出发同一直道去B地,
设小丽出发第时,
小丽、小明离B地的距离分别为、,与x之间的数表达式,与x之间的函数表达式是.
(1)小丽出发时,小明离A地的距离为
.
(2)小丽发至小明到达B地这段时间内,两人何时相距最近?最近距离是多少?
18.网络销售已经成为一种热门的销售方式为了减少农产品的库存,我市市长亲自在某网络平台上进行直播销售大别山牌板栗.为提高大家购买的积极性,直播时,板栗公司每天拿出2000元现金,作为红包发给购买者.已知该板栗的成本价格为6元,每日销售量与销售单价x(元)满足关系式:.经销售发现,销售单价不低于成本价格且不高于30元.当每日销售量不低于时,每千克成本将降低1元设板栗公司销售该板栗的日获利为W(元).
(1)请求出日获利W与销售单价x之间的函数关系式
(2)当销售单价定为多少时,销售这种板栗日获利最大?最大利润为多少元?
(3)当元时,网络平台将向板栗公可收取a元的相关费用,若此时日获利的最大值为42100元,求a的值.
参考答案
1.D
2.C
3.A
4.C
5.B
6.B
7.C
8.D
9.C
10.A
11.
12.15
13.2
14.0.5
15.
16.80
17.(1)250;(2)当小丽出发第时,两人相距最近,最近距离是
18.(1);(2)当销售单价定为28元时,日获利最大,且最大为46400元;(3)
同课章节目录
