冀教版数学七年级上册 1.11 有理数的混合运算 学案+当堂检测(含答案)
文档属性
| 名称 | 冀教版数学七年级上册 1.11 有理数的混合运算 学案+当堂检测(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 252.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览


文档简介
1.11
有理数的混合运算
学习目标:
1.掌握有理数混合运算的顺序,熟练地进行有理数的混合运算;(重点、难点)
2.能利用运算律简化有理数的混合运算;
(难点)
3.能利用有理数的混合运算解决实际问题.
学习重点:掌握有理数混合运算的顺序.
学习难点:进行有理数的混合运算.
知识链接
1.计算
;?
(2);
(3)-7+3-6;?
(4)(-3)×(-8)×25;
(5)(-616)÷(-28);
(6)-100-27;
2.小学阶段四则混合运算的运算法则是什么??
?先算__________,再算______________,如果有___________,先算_________________.
3.用数学语言(字母)来表示各种运算律:
加法交换律_________________________;
加法结合律_________________________;
乘法交换律_________________________;
乘法结合律_________________________;
(5)乘法对加法的分配律_________________________________.
新知预习
观察与思考
1.观察式子,里面包含了哪几种运算?
算式中,含有有理数的______、_______、_______、________及_______运算,这样的运算叫做有理数的混合运算.
2.有理数的混合运算,应该按照什么顺序来计算?
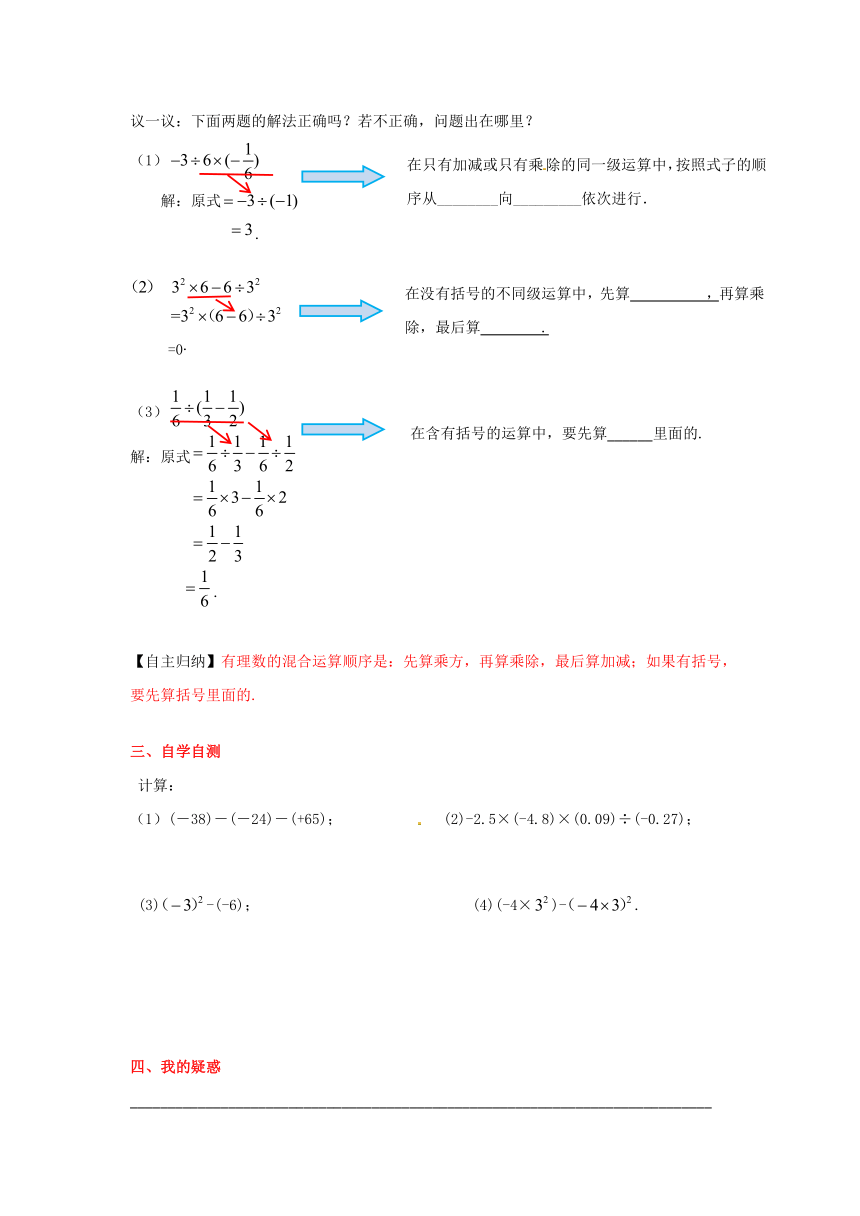
议一议:下面两题的解法正确吗?若不正确,问题出在哪里?
(1)
解:原式
.
=0.
(3)
解:原式
.
【自主归纳】有理数的混合运算顺序是:先算乘方,再算乘除,最后算加减;如果有括号,要先算括号里面的.
三、自学自测
计算:
(1)(-38)-(-24)-(+65);
(2)-2.5×(-4.8)×(0.09)÷(-0.27);
(3)-(-6);?
(4)(-4×)-.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:有理数的混合运算
例1:计算
;
(2).
【归纳总结】简单的有理数混合运算题,要按照运算法则和运算顺序运算,同时要注意两个“统一”,一是统一计算符号,即都用加法或乘法计算;二是统一成分数,即带分数化为假分数或拆成整数与分数的和的形式,存在小数和分数两种形式,统一化为分数,便于约分计算.
【针对训练】
计算
(1)
;
(2).
探究点2:利用运算律简化运算
例2:计算
(1)(-85)×(-25)×(-4);
(2)
(-8)×(-12)×(-0.125)×(-)×(-0.1).
【归纳总结】
几个数相乘时,常把互为倒数或积为整数的数先结合,以便简化计算.
例3:计算
;
.
提示:(1)中前半部分可以直接运用分配律,后半部分可以逆用分配律.
(2)中前半部分可以将分数拆成整数与其真分数之差,后半部分可以将整数拆成两个整数之和,并使其中一个正数能与分数的分母约分.然后利用分配律进行计算.
【归纳总结】正确利用分配律,可减少运算量,提高解题的速度与正确率.
【针对训练】
计算:
(1)2×(-)÷(-2)
(2);
(3).
二、课堂小结
内容
运算顺序
先算________,再算_________,最后算________;如果有括号,要先算____________的.
注意事项
一:统一计算符号,即都用加法或乘法计算;
二:统一成分数,即带分数化为假分数或拆成整数与分数的和的形式,存在小数和分数两种形式,统一化为分数,便于约分计算.
三:合理使用运算律,简化运算.
1.计算(
)
A.-1000
B.1000
C.30
D.-30
2.计算(
)
A.0
B.-54
C.-72
D.-18
3.计算
A.1
B.-25
C.-5
D.25
4.下列等式成立的是(
)
A.100÷×(-7)=100÷
B.100÷×(-7)=100×7×(-7)
C.100÷×(-7)=100××7
D.100÷×(-7)=100×7×7
5.计算:
(1)-20÷5×+5×(-3)÷15;
(2)
;
(3)
;
(4){1+[]×(-2)4}÷(-);
(5)
.
6.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、
3、
5、
+4、
8、
+6、
3、6、
4、
+10.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
当堂检测参考答案:
A
2.B
3.D
4.B
5.(1)-2;
(2)
0;
(3)
-1;
(4)
;
(5)
70.
6.解:(1)+9+(-3)+(-5)+(+4)+(-8)+(+6)+(-3)+(-6)+(-4)+(+10)
=
9+4+10+-3-5-8-3-4+6-6
=0(千米).
(2)(9+3+5+4+8+6+3+6+4+10)×2.4
=58×2.4
=139.2(元).
答:(1)将最后一名乘客送到目的地,出租车就在鼓楼出发点.
(2)司机一个下午的营业额是139.2元.
有理数的混合运算
学习目标:
1.掌握有理数混合运算的顺序,熟练地进行有理数的混合运算;(重点、难点)
2.能利用运算律简化有理数的混合运算;
(难点)
3.能利用有理数的混合运算解决实际问题.
学习重点:掌握有理数混合运算的顺序.
学习难点:进行有理数的混合运算.
知识链接
1.计算
;?
(2);
(3)-7+3-6;?
(4)(-3)×(-8)×25;
(5)(-616)÷(-28);
(6)-100-27;
2.小学阶段四则混合运算的运算法则是什么??
?先算__________,再算______________,如果有___________,先算_________________.
3.用数学语言(字母)来表示各种运算律:
加法交换律_________________________;
加法结合律_________________________;
乘法交换律_________________________;
乘法结合律_________________________;
(5)乘法对加法的分配律_________________________________.
新知预习
观察与思考
1.观察式子,里面包含了哪几种运算?
算式中,含有有理数的______、_______、_______、________及_______运算,这样的运算叫做有理数的混合运算.
2.有理数的混合运算,应该按照什么顺序来计算?
议一议:下面两题的解法正确吗?若不正确,问题出在哪里?
(1)
解:原式
.
=0.
(3)
解:原式
.
【自主归纳】有理数的混合运算顺序是:先算乘方,再算乘除,最后算加减;如果有括号,要先算括号里面的.
三、自学自测
计算:
(1)(-38)-(-24)-(+65);
(2)-2.5×(-4.8)×(0.09)÷(-0.27);
(3)-(-6);?
(4)(-4×)-.
四、我的疑惑
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
要点探究
探究点1:有理数的混合运算
例1:计算
;
(2).
【归纳总结】简单的有理数混合运算题,要按照运算法则和运算顺序运算,同时要注意两个“统一”,一是统一计算符号,即都用加法或乘法计算;二是统一成分数,即带分数化为假分数或拆成整数与分数的和的形式,存在小数和分数两种形式,统一化为分数,便于约分计算.
【针对训练】
计算
(1)
;
(2).
探究点2:利用运算律简化运算
例2:计算
(1)(-85)×(-25)×(-4);
(2)
(-8)×(-12)×(-0.125)×(-)×(-0.1).
【归纳总结】
几个数相乘时,常把互为倒数或积为整数的数先结合,以便简化计算.
例3:计算
;
.
提示:(1)中前半部分可以直接运用分配律,后半部分可以逆用分配律.
(2)中前半部分可以将分数拆成整数与其真分数之差,后半部分可以将整数拆成两个整数之和,并使其中一个正数能与分数的分母约分.然后利用分配律进行计算.
【归纳总结】正确利用分配律,可减少运算量,提高解题的速度与正确率.
【针对训练】
计算:
(1)2×(-)÷(-2)
(2);
(3).
二、课堂小结
内容
运算顺序
先算________,再算_________,最后算________;如果有括号,要先算____________的.
注意事项
一:统一计算符号,即都用加法或乘法计算;
二:统一成分数,即带分数化为假分数或拆成整数与分数的和的形式,存在小数和分数两种形式,统一化为分数,便于约分计算.
三:合理使用运算律,简化运算.
1.计算(
)
A.-1000
B.1000
C.30
D.-30
2.计算(
)
A.0
B.-54
C.-72
D.-18
3.计算
A.1
B.-25
C.-5
D.25
4.下列等式成立的是(
)
A.100÷×(-7)=100÷
B.100÷×(-7)=100×7×(-7)
C.100÷×(-7)=100××7
D.100÷×(-7)=100×7×7
5.计算:
(1)-20÷5×+5×(-3)÷15;
(2)
;
(3)
;
(4){1+[]×(-2)4}÷(-);
(5)
.
6.某一出租车一天下午以鼓楼为出发地在东西方向营运,向东为正,向西为负,行车里程(单位:km)依先后次序记录如下:+9、
3、
5、
+4、
8、
+6、
3、6、
4、
+10.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
当堂检测参考答案:
A
2.B
3.D
4.B
5.(1)-2;
(2)
0;
(3)
-1;
(4)
;
(5)
70.
6.解:(1)+9+(-3)+(-5)+(+4)+(-8)+(+6)+(-3)+(-6)+(-4)+(+10)
=
9+4+10+-3-5-8-3-4+6-6
=0(千米).
(2)(9+3+5+4+8+6+3+6+4+10)×2.4
=58×2.4
=139.2(元).
答:(1)将最后一名乘客送到目的地,出租车就在鼓楼出发点.
(2)司机一个下午的营业额是139.2元.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
