沪科版数学八年级上册 14.2.2 两角及其夹边分别相等的两个三角形学案(无答案)
文档属性
| 名称 | 沪科版数学八年级上册 14.2.2 两角及其夹边分别相等的两个三角形学案(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 197.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 12:52:54 | ||
图片预览

文档简介
14.2
三角形全等的判定
2.两角及其边角分别相等的两个三角形
一:导学目标
掌握全等三角形的判断方法-------ASA。
能利用ASA判断全等三角形,并解决一些证角与边相等有关的的题目。
能结合其它判定方法综合解决一些边角有关的题型。
学会作一个角等于另一个角。
二:导学问题
(一)复习导学
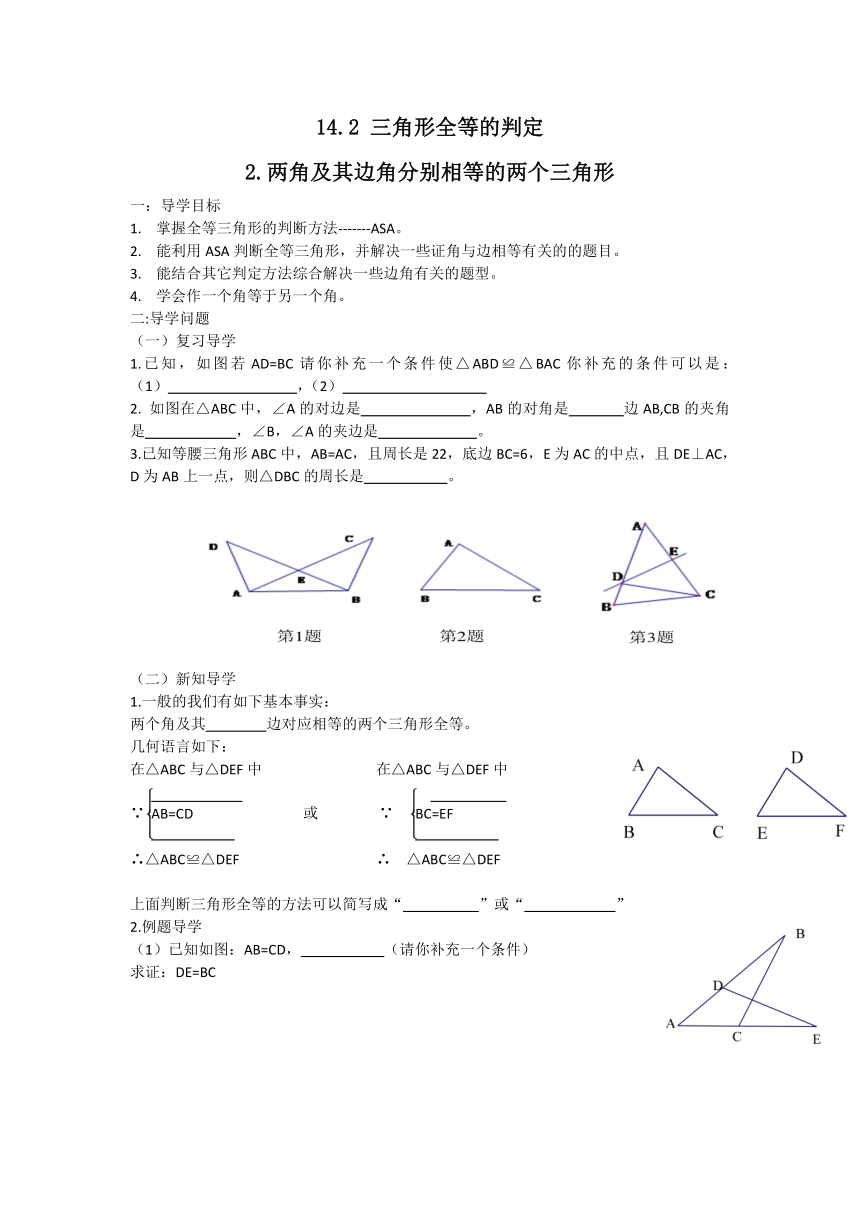
1.已知,如图若AD=BC请你补充一个条件使△ABD≌△BAC你补充的条件可以是:(1)
,(2)
2.
如图在△ABC中,∠A的对边是
,AB的对角是
边AB,CB的夹角是
,∠B,∠A的夹边是
。
3.已知等腰三角形ABC中,AB=AC,且周长是22,底边BC=6,E为AC的中点,且DE⊥AC,D为AB上一点,则△DBC的周长是
。
(二)新知导学
1.一般的我们有如下基本事实:
两个角及其
边对应相等的两个三角形全等。
几何语言如下:
在△ABC与△DEF中
在△ABC与△DEF中
∵
或
∵
∴△ABC≌△DEF
∴
△ABC≌△DEF
上面判断三角形全等的方法可以简写成“
”或“
”
2.例题导学
(1)已知如图:AB=CD,
(请你补充一个条件)
求证:DE=BC
(2)已知如图:∠B=∠E,AB=AE,
或
(请你补充一个条件,并选一个较难的进行证明)。求证:AD=AC
(3)已知如图,AD,BC相交于点E,BE=AC
AB∥CD
求证:AE=ED
四:练习导学
已知如图,AB⊥BD,DE⊥BD,AC⊥CE,AB=CD.
求证:AC=CE
已知如图,∠1=∠2,∠ACB=∠DBC,
求证AE=DE
已知:如图,AEFB在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B.
求证:CE=DF
4.已知如图,CE⊥AB于点E,BD⊥AC于点D,BD、CE交于点O,且AO平分∠BAC,
(1)图中有多少对全等的三角形?请你一一列举出来(不要求说明理由)
(2)小明说:欲证BE=CD,可先证明△AOE≌△AOD得到AE=AD,再证明△ADB?≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗??如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?若有,请仿照小明的说法具体说一说你的想法.
5.小明想测一块泥地AB的长度(如图所示),它在AB的垂线BM上分别取C、D两点,使CD=BC,再过D点作出BM的垂线DN,并在DN上找一点E,使A、C、E三点共线,这使所测得的DE的长度就是这块泥地AB的长度,你能说明原因吗?
6.
如图1,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是选
号,理由是
。
三角形全等的判定
2.两角及其边角分别相等的两个三角形
一:导学目标
掌握全等三角形的判断方法-------ASA。
能利用ASA判断全等三角形,并解决一些证角与边相等有关的的题目。
能结合其它判定方法综合解决一些边角有关的题型。
学会作一个角等于另一个角。
二:导学问题
(一)复习导学
1.已知,如图若AD=BC请你补充一个条件使△ABD≌△BAC你补充的条件可以是:(1)
,(2)
2.
如图在△ABC中,∠A的对边是
,AB的对角是
边AB,CB的夹角是
,∠B,∠A的夹边是
。
3.已知等腰三角形ABC中,AB=AC,且周长是22,底边BC=6,E为AC的中点,且DE⊥AC,D为AB上一点,则△DBC的周长是
。
(二)新知导学
1.一般的我们有如下基本事实:
两个角及其
边对应相等的两个三角形全等。
几何语言如下:
在△ABC与△DEF中
在△ABC与△DEF中
∵
或
∵
∴△ABC≌△DEF
∴
△ABC≌△DEF
上面判断三角形全等的方法可以简写成“
”或“
”
2.例题导学
(1)已知如图:AB=CD,
(请你补充一个条件)
求证:DE=BC
(2)已知如图:∠B=∠E,AB=AE,
或
(请你补充一个条件,并选一个较难的进行证明)。求证:AD=AC
(3)已知如图,AD,BC相交于点E,BE=AC
AB∥CD
求证:AE=ED
四:练习导学
已知如图,AB⊥BD,DE⊥BD,AC⊥CE,AB=CD.
求证:AC=CE
已知如图,∠1=∠2,∠ACB=∠DBC,
求证AE=DE
已知:如图,AEFB在同一条直线上,CE⊥AB,DF⊥AB,AE=BF,∠A=∠B.
求证:CE=DF
4.已知如图,CE⊥AB于点E,BD⊥AC于点D,BD、CE交于点O,且AO平分∠BAC,
(1)图中有多少对全等的三角形?请你一一列举出来(不要求说明理由)
(2)小明说:欲证BE=CD,可先证明△AOE≌△AOD得到AE=AD,再证明△ADB?≌△AEC得到AB=AC,然后利用等式的性质即可得到BE=CD,请问他的说法正确吗??如果不正确,请说明理由;如果正确,请按他的思路写出推导过程.
(3)要得到BE=CD,你还有其他的思路吗?若有,请仿照小明的说法具体说一说你的想法.
5.小明想测一块泥地AB的长度(如图所示),它在AB的垂线BM上分别取C、D两点,使CD=BC,再过D点作出BM的垂线DN,并在DN上找一点E,使A、C、E三点共线,这使所测得的DE的长度就是这块泥地AB的长度,你能说明原因吗?
6.
如图1,小明把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是选
号,理由是
。
