冀教版数学九年级上册26.4解直角三角形的应用 课件 (共17张PPT)
文档属性
| 名称 | 冀教版数学九年级上册26.4解直角三角形的应用 课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 607.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-13 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
能够用锐角三角函数的知识解决与方位
有关的实际问题
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
任务一:组内订正学案上“做一做”的答案。
方
式:实物投影展示一位同学的解答过程。
不会的同学,小组内讨论后完成。
时
间:5
分钟。
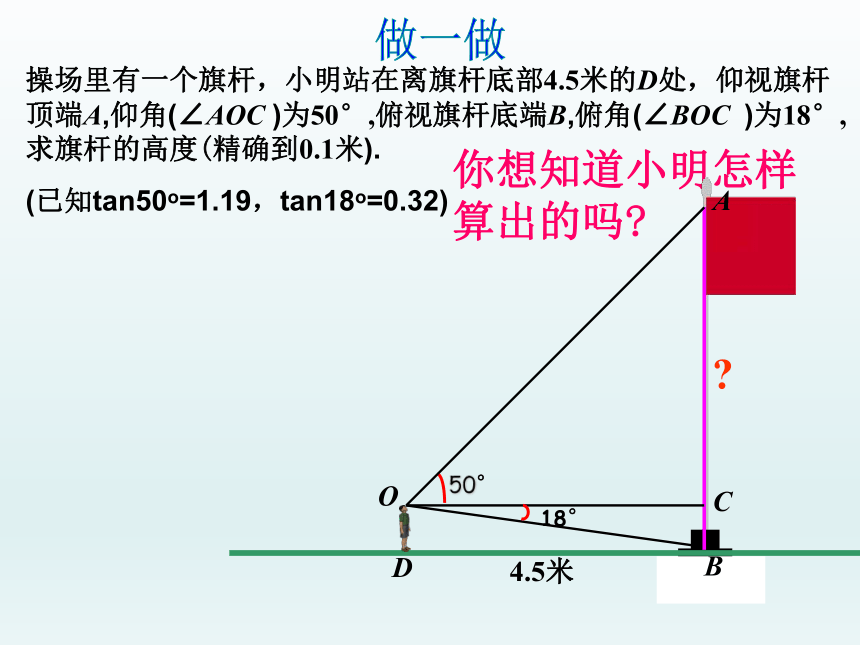
操场里有一个旗杆,小明站在离旗杆底部4.5米的D处,仰视旗杆顶端A,仰角(∠AOC
)为50°,俯视旗杆底端B,俯角(∠BOC
)为18°,求旗杆的高度(精确到0.1米).
(已知tan50o=1.19,tan18o=0.32)
你想知道小明怎样算出的吗?
4.5米
?
50°
18°
O
C
A
B
D
任务二:独立思考,完成例1。
方
式:完成后举手,讲解思路清晰加2分。
时
间:12
分钟。
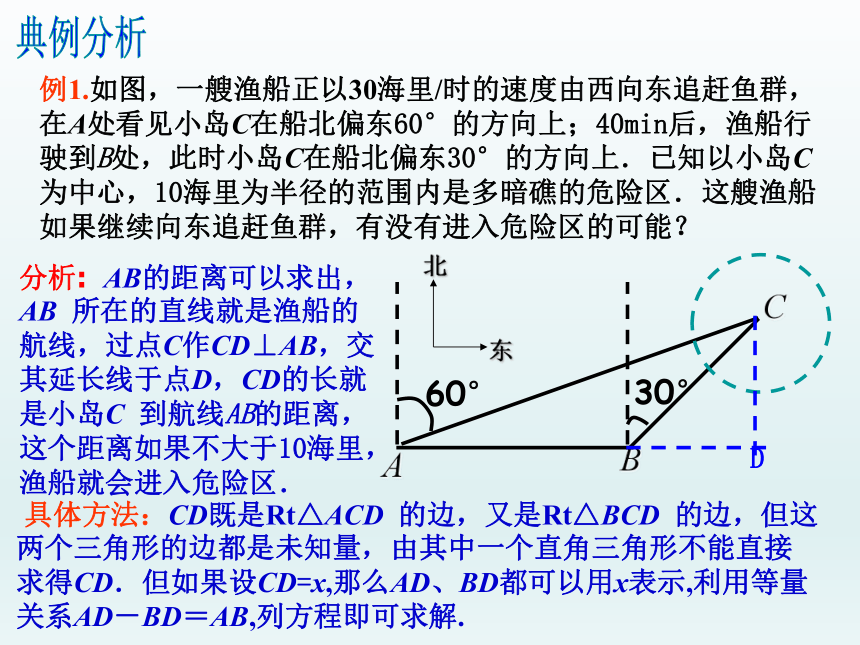
例1.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船北偏东60°的方向上;40min后,渔船行驶到B处,此时小岛C在船北偏东30°的方向上.已知以小岛C为中心,10海里为半径的范围内是多暗礁的危险区.这艘渔船如果继续向东追赶鱼群,有没有进入危险区的可能?
北
东
B
60°
30°
A
C
分析:
AB的距离可以求出,AB
所在的直线就是渔船的航线,过点C作CD⊥AB,交其延长线于点D,CD的长就是小岛C
到航线AB的距离,这个距离如果不大于10海里,渔船就会进入危险区.
D
具体方法:CD既是Rt△ACD
的边,又是Rt△BCD
的边,但这两个三角形的边都是未知量,由其中一个直角三角形不能直接求得CD.但如果设CD=x,那么AD、BD都可以用x表示,利用等量关系AD-BD=AB,列方程即可求解.
解:如图,根据题意可知,∠CAD=30°,∠DBC=60°,
AB=
=20m.设CD=x,
在Rt△ACD中,
tan
∠CAD=
,
在Rt△BCD中,
tan
∠CBD=
,
∴AD=
,
BD=
∵AD-BD=AB,
∴
∵
,
所以这艘渔船继续向东航行,不会进入危险区。
北
东
B
60°
30°
A
C
D
例1.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船北偏东60°的方向上;40min后,渔船行驶到B处,此时小岛C在船北偏东30°的方向上.已知以小岛C为中心,10海里为半径的范围内是多暗礁的危险区.这艘渔船如果继续向东追赶鱼群,有没有进入危险区的可能?
北
东
B
60°
30°
A
C
D
还有其他方法吗?
任务三:做“举一反三”,要求有完整的解答过程。
方
式:同桌交换,订正答案,统计完成情况。
时
间:10
分钟。
(2014建邺区一模)如图,为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为27°,然后他向气球方向前进了50m,此时观测气球,测得仰角为45°.若小明的眼睛离地面1.6m,求气球离地面的高度(精确到0.1m).
(下列数据供参考:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
举一反三
解:设CD=x,在Rt△BCD中,
∵∠CBD=45°∴BD=CD=x,
在Rt△ACD中∵∠A=27°,
∴
=tan27°,则AD=
,?
∵AB=50m,∴AD﹣BD=
﹣x=50,
解得:x≈52.0,?
∴气球离地面的高度约为52.0+1.6=53.6(m).
答:气球离地面的高度约为53.6m.
任务四:独立完成例2。
方
式:找一位同学板演、讲解。
格式完整,解答正确加2分。
时
间:8
分钟。
D
α
β
A
B
C
B
C
120米
D
例2:测河的宽度
想一想:如何求河宽AD?(用含α,β的三角函数表示)
在运用锐角三角函数的知识解决实际问题时,你是如何思考的?
主要步骤:
1.分析实际问题中某些名词、概念的意义,正确理解条件和结论的关系;
2.将现实问题转化为数学问题,建立直角三角形模型;
3.根据条件特点,选用适当的锐角三角函数解决问题;
4.
写出解答过程与答案
.
思考·探索·交流
1.如图,MN表示某引水工程的一段设计路线,从M到N
的走向为南偏东30°,在M的南偏东60°的方向上有一
点
A,以
A为圆心、500
m为半径的圆形区域为居民区.
取MN上另一点B,测得BA的方向为南偏东
75°.
已知MB=400
m,通过计算回答,如果不改变方向,输水路线是否会穿过居民区?
60o
D
60o
D
E
α
A
B
C
α
B
C
A
α
α
C
A
B
β
D
β
D
α
C
A
B
翻折
B
C
A
α
β
D
B
C
A
α
β
D
B
C
A
α
β
D
旋转
E
α
C
A
B
β
D
α
C
A
B
β
D
α
C
A
B
β
D
α
β
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
β
锐角三角函数应用常见的几种图形
能够用锐角三角函数的知识解决与方位
有关的实际问题
(2)两锐角之间的关系
∠A+∠B=90°
(3)边角之间的关系
(1)三边之间的关系
A
B
a
b
c
C
任务一:组内订正学案上“做一做”的答案。
方
式:实物投影展示一位同学的解答过程。
不会的同学,小组内讨论后完成。
时
间:5
分钟。
操场里有一个旗杆,小明站在离旗杆底部4.5米的D处,仰视旗杆顶端A,仰角(∠AOC
)为50°,俯视旗杆底端B,俯角(∠BOC
)为18°,求旗杆的高度(精确到0.1米).
(已知tan50o=1.19,tan18o=0.32)
你想知道小明怎样算出的吗?
4.5米
?
50°
18°
O
C
A
B
D
任务二:独立思考,完成例1。
方
式:完成后举手,讲解思路清晰加2分。
时
间:12
分钟。
例1.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船北偏东60°的方向上;40min后,渔船行驶到B处,此时小岛C在船北偏东30°的方向上.已知以小岛C为中心,10海里为半径的范围内是多暗礁的危险区.这艘渔船如果继续向东追赶鱼群,有没有进入危险区的可能?
北
东
B
60°
30°
A
C
分析:
AB的距离可以求出,AB
所在的直线就是渔船的航线,过点C作CD⊥AB,交其延长线于点D,CD的长就是小岛C
到航线AB的距离,这个距离如果不大于10海里,渔船就会进入危险区.
D
具体方法:CD既是Rt△ACD
的边,又是Rt△BCD
的边,但这两个三角形的边都是未知量,由其中一个直角三角形不能直接求得CD.但如果设CD=x,那么AD、BD都可以用x表示,利用等量关系AD-BD=AB,列方程即可求解.
解:如图,根据题意可知,∠CAD=30°,∠DBC=60°,
AB=
=20m.设CD=x,
在Rt△ACD中,
tan
∠CAD=
,
在Rt△BCD中,
tan
∠CBD=
,
∴AD=
,
BD=
∵AD-BD=AB,
∴
∵
,
所以这艘渔船继续向东航行,不会进入危险区。
北
东
B
60°
30°
A
C
D
例1.如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船北偏东60°的方向上;40min后,渔船行驶到B处,此时小岛C在船北偏东30°的方向上.已知以小岛C为中心,10海里为半径的范围内是多暗礁的危险区.这艘渔船如果继续向东追赶鱼群,有没有进入危险区的可能?
北
东
B
60°
30°
A
C
D
还有其他方法吗?
任务三:做“举一反三”,要求有完整的解答过程。
方
式:同桌交换,订正答案,统计完成情况。
时
间:10
分钟。
(2014建邺区一模)如图,为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为27°,然后他向气球方向前进了50m,此时观测气球,测得仰角为45°.若小明的眼睛离地面1.6m,求气球离地面的高度(精确到0.1m).
(下列数据供参考:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51)
举一反三
解:设CD=x,在Rt△BCD中,
∵∠CBD=45°∴BD=CD=x,
在Rt△ACD中∵∠A=27°,
∴
=tan27°,则AD=
,?
∵AB=50m,∴AD﹣BD=
﹣x=50,
解得:x≈52.0,?
∴气球离地面的高度约为52.0+1.6=53.6(m).
答:气球离地面的高度约为53.6m.
任务四:独立完成例2。
方
式:找一位同学板演、讲解。
格式完整,解答正确加2分。
时
间:8
分钟。
D
α
β
A
B
C
B
C
120米
D
例2:测河的宽度
想一想:如何求河宽AD?(用含α,β的三角函数表示)
在运用锐角三角函数的知识解决实际问题时,你是如何思考的?
主要步骤:
1.分析实际问题中某些名词、概念的意义,正确理解条件和结论的关系;
2.将现实问题转化为数学问题,建立直角三角形模型;
3.根据条件特点,选用适当的锐角三角函数解决问题;
4.
写出解答过程与答案
.
思考·探索·交流
1.如图,MN表示某引水工程的一段设计路线,从M到N
的走向为南偏东30°,在M的南偏东60°的方向上有一
点
A,以
A为圆心、500
m为半径的圆形区域为居民区.
取MN上另一点B,测得BA的方向为南偏东
75°.
已知MB=400
m,通过计算回答,如果不改变方向,输水路线是否会穿过居民区?
60o
D
60o
D
E
α
A
B
C
α
B
C
A
α
α
C
A
B
β
D
β
D
α
C
A
B
翻折
B
C
A
α
β
D
B
C
A
α
β
D
B
C
A
α
β
D
旋转
E
α
C
A
B
β
D
α
C
A
B
β
D
α
C
A
B
β
D
α
β
A
B
D
C
旋转
60o
D
平移
60o
D
60o
D
60o
D
β
锐角三角函数应用常见的几种图形
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
